Equação de Águas Rasas: mudanças entre as edições
| (134 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
'''Grupo: Gabriel Schmökel e Julia Remus''' | '''Grupo: Gabriel Schmökel e Julia Remus''' | ||
O objetivo deste trabalho é buscar a solução das equações de águas rasas, por meio de métodos de integração numérica, para resolução de equações diferenciais parciais (EDP's) e posteriormente apresentar uma breve interpretação física das soluções. Demonstramos, nesta página, a derivação das equações, junto com a explicação de cada quantidade física presente. A discretização das equações de águas rasas conservativas e não conservativas são feitas por FTCS explícito, também foi aplicado FTCS implícito para as equações em uma forma simplificada, representada pela equação da deriva. Os resultados obtidos para equação simplificada são comparados com a solução exata, e exemplos mais complexos são solucionados para as formas conservativa e não conservativa. Ao final, uma comparação é feita entre os resultados das equações conservativas e dissipativas. | |||
== Introdução == | == Introdução == | ||
As equações de águas rasas têm aplicações físicas na previsão de tsunâmis, em fluxos atmosféricos, ondas de tempestade e fluxos planetários. Na descrição física dos problemas de fluxos de fluído em ondas, as equações de águas rasas em uma dimensão são dadas por: | |||
= | <math>\dfrac{\partial \eta}{\partial t} + \dfrac{\partial u D}{\partial x} = 0 \qquad (1) </math> | ||
<math>\dfrac{\partial \eta u}{\partial t} + \dfrac{\partial \left (\eta u^2 + \dfrac{1}{2}g \eta^2 \right)}{\partial x} = -g \eta \dfrac{\partial h}{\partial x} \qquad (2) </math> | |||
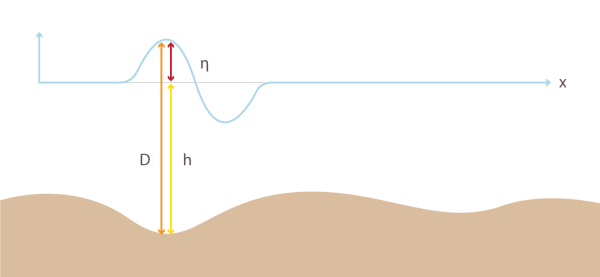
As componentes da equação de águas rasas podem ser melhor interpretadas através da seguinte figura: | |||
[[Arquivo:TSUNAMI3-06.png|600px|center|Componentes das equações de águas rasas]] | |||
<math> \eta = \eta(x,t) </math> corresponde a amplitude da onda, <math> h=h(x) </math> determina a profundidade do mar em repouso, <math> D</math> é o deslocamento total da água, <math> u</math> é a velocidade do fluído. Resolvendo a EDP da equação de águas rasas, obtemos como a amplitude da onda se comporta ao longo do tempo e do espaço. | |||
<math> \eta = \eta(x,t) </math> corresponde a amplitude da onda, <math> h=h(x) </math> determina a profundidade do mar em repouso, <math> D</math> é o deslocamento total da água, <math> u</math> é a velocidade do fluído e | |||
== Teoria == | == Teoria == | ||
===Derivação das Equações de Águas Rasas=== | ===Derivação das Equações de Águas Rasas=== | ||
Iremos demonstrar como chegamos nas equações de águas rasas em duas dimensões, nas formas conservativa e dissipativa, em representações do fluxo de descarga e de velocidade. Posteriormente, tendo as equações em 2D, iremos simplificar elas para a forma unidimensional. Neste processo de demonstração, iremos explicar a interpretação física de cada quantidade presente nas equações. | |||
Para obter as equações de águas rasas devemos partir da equação da continuidade e das equações da quantidade de movimento de Navier-Stokes: | Para obter as equações de águas rasas devemos partir da equação da continuidade e das equações da quantidade de movimento de Navier-Stokes: | ||
<math> \frac{d\rho}{dt} +\nabla . | <math> \nabla . (\rho \mathbf{u}) = \frac{d\rho}{dt} \qquad (3) </math> | ||
<math> \frac{D \mathbf{u}}{Dt} +\frac{1}{\rho}\nabla p +\frac{1}{\rho} \nabla . \boldsymbol{\tau} +\mathbf{g} = 0 \qquad (4) </math> | |||
<math> | A equação da continuidade em (3) descreve o balanço de massas para os elementos de volume infinitesimais que pertencem ao fluído, onde a quantidade do lado esquerdo da equação informa o fluxo de massa que entra e sai pelo elemento de volume, e a quantidade do lado direito está relacionada com a massa que se acumula ao longo do tempo <ref>Equação da continuidade mássica: balanços de massa diferenciais. Bloom Consultoria.Disponível em: <https://www.youtube.com/watch?v=pEip-GvO0LM&list=PL1yqHjPQz-Lqjri07DqZ3RsSWJfICvdiu&index=3></ref>. Nesta expressão <math> \rho </math> é a densidade, e <math> \mathbf u=(u,v,w,t) </math> é o campo de velocidades, onde u,v e w são as velocidades das partículas que compõe o fluído nas direções x,y,z. | ||
As equações de Navier-Stokes em (4) são balanços diferenciais da quantidade de movimento, obtidas através da aplicação da segunda lei de Newton em cada ponto do escoamento <ref>Equação de Navier-Stokes (Parte 1) - Derivadas materiais. | |||
Bloom Consultoria.Disponível em: https://www.youtube.com/watch?v=FLoZODPpayM</ref> <ref>Equação de Navier-Stokes (Parte 2) - Equação diferencial da quantidade de movimento. Bloom Consultoria.Disponível em: https://www.youtube.com/watch?v=e06ZRzdO4iM</ref> <ref>Equação de Navier-Stokes (Parte 3) - Tensões Normais e Cisalhantes. Bloom Consultoria.Disponível em: https://www.youtube.com/watch?v=na2kGOSYNv8</ref>. | |||
<math> | * <math> Du/Dt </math> é a aceleração da partícula fluída ao longo do campo de velocidade <math> \mathbf u=(u,v,w,t) </math>. | ||
* <math> \nabla . \boldsymbol{\tau} / \rho</math> está associado as tensões tangenciais e normais atuando sobre os elementos de volume (<math> \boldsymbol{\tau} </math> é o tensor tensão, as componentes deste tensor são as tensões normais e tangenciais de cisalhamento, expressas por <math> \tau_{ij} </math>, no qual <math> i </math> indica a direção e <math> j </math> o plano normal). | |||
* <math> \nabla p / \rho </math> está associado as pressões que atuam sobre os elementos do fluído. | |||
* <math> \mathbf{g} </math> é o vetor aceleração da gravidade atuando sobre os elementos infinitesimais de volume do fluído. | |||
Introduzindo as condições de contorno <ref>SEGUR, Harvey; YAMAMOTO, Hiroki. Lecture 8: The Shallow-Water Equations.Disponível em: <https://docplayer.net/49487265-Lecture-8-the-shallow-water-equations.html></ref | Introduzindo as condições de contorno para a superfície <math> z(x,y,t) </math> e para a profundidade do oceano <math> h(x,y) </math> <ref>SEGUR, Harvey; YAMAMOTO, Hiroki. Lecture 8: The Shallow-Water Equations.Disponível em: <https://docplayer.net/49487265-Lecture-8-the-shallow-water-equations.html></ref>: | ||
<math> \frac{D \eta}{Dt} = \frac{\partial \eta}{\partial t} +\mathbf{v} . \nabla \eta = w </math> , onde <math> z= \eta(x,y,t) \qquad ( | <math> \frac{D \eta}{Dt} = \frac{\partial \eta}{\partial t} +\mathbf{v} . \nabla \eta = w </math> , onde <math> z= \eta(x,y,t) \qquad (5) </math> | ||
<math> \mathbf{u} . \nabla (z + h(x,y)) = 0 </math> , onde <math> z =-h(x,y) \qquad ( | <math> \mathbf{u} . \nabla (z + h(x,y)) = 0 </math> , onde <math> z =-h(x,y) \qquad (6)</math> | ||
<math> \eta </math> é o deslocamento vertical da água sobre a superfície em repouso, <math> \mathbf{v} = (x,y,0) </math> é o vetor velocidade do fluído nas direções horizontais x e y. | <math> \eta </math> é o deslocamento vertical da água sobre a superfície em repouso, <math> \mathbf{v} = (x,y,0) </math> é o vetor velocidade do fluído nas direções horizontais x e y. | ||
A equação da continuidade em ( | A equação da continuidade em (3) pode ser simplificada pelo fato do fluído ser incompressível, isto implica que a densidade <math> \rho </math> é constante. | ||
<math> \nabla . \mathbf{u} = 0 \qquad ( | <math> \nabla . \mathbf{u} = 0 \qquad (7) </math> | ||
Integrando a expressão da continuidade em ( | Integrando a expressão da continuidade em (7), utilizando a regra da integral de Leibniz <ref>Leibniz integral rule. Disponível em: https://en.wikipedia.org/wiki/Leibniz_integral_rule </ref>, com os limites indo de <math> -h(x,y) </math> até <math> \eta (x,y,t) </math> chegamos na seguinte expressão: | ||
<math> \int_{-h}^{\eta} \nabla . \mathbf{u} = \int_{-h}^{\eta} \Big(\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z}\Big)dz = | <math> \int_{-h}^{\eta} \nabla . \mathbf{u} = \int_{-h}^{\eta} \Big(\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z}\Big)dz = | ||
\frac{\partial}{\partial x} \int_{-h}^{\eta} u dz + \frac{\partial}{\partial y} \int_{-h}^{\eta} v dz +w \Big |_{-h}^{\eta} + \mathbf{u} . \nabla (z + h(x,y)) \Big |_{-h}^{\eta} -u \Big |_{-h}^{\eta} \frac{\partial \eta}{\partial x} -v \Big |_{-h}^{\eta} \frac{\partial \eta}{\partial y} \qquad ( | \frac{\partial}{\partial x} \int_{-h}^{\eta} u dz + \frac{\partial}{\partial y} \int_{-h}^{\eta} v dz +w \Big |_{-h}^{\eta} + \mathbf{u} . \nabla (z + h(x,y)) \Big |_{-h}^{\eta} -u \Big |_{-h}^{\eta} \frac{\partial \eta}{\partial x} -v \Big |_{-h}^{\eta} \frac{\partial \eta}{\partial y} \qquad (8) </math> | ||
Teorema de Leibniz: | Teorema de Leibniz: | ||
<math>\frac{d}{dx} \left (\int_{a(x)}^{b(x)} f(x,t)\,dt \right )= f\big(x,b(x)\big)\cdot \frac{d}{dx} b(x) - f\big(x,a(x)\big)\cdot \frac{d}{dx} a(x) + \int_{a(x)}^{b(x)}\frac{\partial}{\partial x} f(x,t) \,dt \qquad ( | <math>\frac{d}{dx} \left (\int_{a(x)}^{b(x)} f(x,t)\,dt \right )= f\big(x,b(x)\big)\cdot \frac{d}{dx} b(x) - f\big(x,a(x)\big)\cdot \frac{d}{dx} a(x) + \int_{a(x)}^{b(x)}\frac{\partial}{\partial x} f(x,t) \,dt \qquad (9)</math> | ||
Substituindo as condições de contorno da profundidade ( | Substituindo as condições de contorno da profundidade (6) em (8) obtemos: | ||
<math> \frac{\partial}{\partial x} \int_{-h}^{\eta} u dz + \frac{\partial}{\partial y} \int_{-h}^{\eta} v dz - w \Big |_{eta} -\mathbf{v} . \nabla \eta = 0 \qquad ( | <math> \frac{\partial}{\partial x} \int_{-h}^{\eta} u dz + \frac{\partial}{\partial y} \int_{-h}^{\eta} v dz - w \Big |_{eta} -\mathbf{v} . \nabla \eta = 0 \qquad (10) </math> | ||
Substituindo a condição de contorno da superfície ( | Substituindo a condição de contorno da superfície (5) em (10): | ||
<math> \frac{\partial}{\partial x} \int_{-h}^{\eta} u dz + \frac{\partial}{\partial y} \int_{-h}^{\eta} v dz + \frac{\partial \eta}{\partial t} = \frac{\partial u (\eta + h)}{\partial x}+ \frac{\partial v (\eta + h)}{\partial y} + \frac{\partial \eta}{\partial t} = \frac{\partial uD}{\partial x}+ \frac{\partial vD}{\partial y} + \frac{\partial \eta}{\partial t} </math> | <math> \frac{\partial}{\partial x} \int_{-h}^{\eta} u dz + \frac{\partial}{\partial y} \int_{-h}^{\eta} v dz + \frac{\partial \eta}{\partial t} = \frac{\partial u (\eta + h)}{\partial x}+ \frac{\partial v (\eta + h)}{\partial y} + \frac{\partial \eta}{\partial t} = \frac{\partial uD}{\partial x}+ \frac{\partial vD}{\partial y} + \frac{\partial \eta}{\partial t} </math> | ||
<math> \Rightarrow \frac{\partial \eta}{\partial t} + \frac{\partial uD}{\partial x}+ \frac{\partial vD}{\partial y} = 0 \qquad ( | <math> \Rightarrow \frac{\partial \eta}{\partial t} + \frac{\partial uD}{\partial x}+ \frac{\partial vD}{\partial y} = 0 \qquad (11) </math> | ||
(11) é a primeira das equações das águas rasas que obtemos, onde <math> D </math> é o comprimento da água total do fundo do oceano até a amplitude da onda. | |||
Podemos expressar (11) através do fluxo de descarga nas direções x e y, estas quantidades estão relacionadas com as velocidades da seguinte forma <ref name=MANUAL> IMAMURA, Fumihiko.Tsunami Modelling Manual.Disponível em: http://www.tsunami.civil.tohoku.ac.jp/hokusai3/J/projects/manual-ver-3.1.pdf </ref>: | |||
<math> M = \frac{\partial}{\partial x} \int_{-h}^{\eta} u dz = uD \qquad (12) </math> | |||
<math> | <math> N = \frac{\partial}{\partial y} \int_{-h}^{\eta} v dz = vD \qquad (13) </math> | ||
Substituindo (12) e (13) em (11) chegamos na representação do fluxo de descarga para uma das equações de águas rasas. | |||
<math> \Rightarrow \frac{\partial \eta}{\partial t} + \frac{\partial M}{\partial x}+ \frac{\partial N}{\partial y} = 0 \qquad (14) </math> | |||
Conhecendo as taxas dos fluxos de descarga em relação as regiões espaciais, podemos determinar a taxa da variação da amplitude da onda em relação ao tempo. | |||
Vamos buscar obter as outras duas equações de águas rasas restantes, a partir das quantidades de movimento de Navier-Stokes. Nas componentes x,y e z temos: | |||
<math> \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} | <math> \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} | ||
+ w\frac{\partial u}{\partial z} +\frac{1}{\rho}\frac{\partial P}{\partial x} +g_x = 0 \qquad ( | + w\frac{\partial u}{\partial z} +\frac{1}{\rho}\frac{\partial P}{\partial x} +g_x = 0 \qquad (15) </math> | ||
<math> \frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} | <math> \frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} | ||
+ w\frac{\partial v}{\partial z} +\frac{1}{\rho}\frac{\partial P}{\partial x} +g_y = 0 \qquad ( | + w\frac{\partial v}{\partial z} +\frac{1}{\rho}\frac{\partial P}{\partial x} +g_y = 0 \qquad (16) </math> | ||
<math> \frac{1}{\rho}\frac{\partial P}{\partial x} +g_z = 0 \qquad ( | <math> \frac{1}{\rho}\frac{\partial P}{\partial x} +g_z = 0 \qquad (17) </math> | ||
Na componente z em ( | Na componente z em (17) não consideramos a aceleração das partículas, pois a aceleração da gravidade é muito maior. Também tomamos como nulo as componentes <math> g_x</math> e <math> g_y</math> em (15) e (16), assim passamos a definir <math> g_z = g </math>. Neste momento estamos desconsiderando as forças de fricção, por isso o tensor tensão também é nulo. | ||
Resolvendo equação diferencial da componente z em ( | Resolvendo equação diferencial da componente z em (17) podemos obter a pressão, a qual é hidrostática. | ||
<math> \partial P = \rho g \partial z \Rightarrow P = \rho g (\eta - z) \qquad ( | <math> \partial P = \rho g \partial z \Rightarrow P = \rho g (\eta - z) \qquad (18) </math> | ||
Substituindo a pressão em ( | Substituindo a pressão em (15): | ||
<math> \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} | <math> \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} | ||
+ w\frac{\partial u}{\partial z} +g \frac{\partial \eta}{\partial x} =0 \qquad ( | + w\frac{\partial u}{\partial z} +g \frac{\partial \eta}{\partial x} =0 \qquad (19) </math> | ||
Integrando a expressão ( | Integrando a expressão (19), utilizando a regra da integral de Leibniz e as condições de contorno (5) e (6), com os limites indo de <math>-h(x,y)</math> até <math>\eta(x,y,t)</math> chegamos em outra das equações de águas rasas: | ||
<math> \frac{\partial uD}{\partial t} + \frac{\partial u^{2}D}{\partial x} + \frac{\partial uvD}{\partial y} | <math> \frac{\partial uD}{\partial t} + \frac{\partial u^{2}D}{\partial x} + \frac{\partial uvD}{\partial y} | ||
+ \frac{g}{2} \frac{\partial D^2}{\partial x} =0 \qquad ( | + \frac{g}{2} \frac{\partial D^2}{\partial x} =0 \qquad (20) </math> | ||
Generalizando a equação ( | Generalizando a equação (20), para a componente y, obtemos a última das equações de águas rasas: | ||
<math> \frac{\partial vD}{\partial t} + \frac{\partial v^{2}D}{\partial y} + \frac{\partial uvD}{\partial x} | <math> \frac{\partial vD}{\partial t} + \frac{\partial v^{2}D}{\partial y} + \frac{\partial uvD}{\partial x} | ||
+ \frac{g}{2} \frac{\partial D^2}{\partial y} =0 \qquad ( | + \frac{g}{2} \frac{\partial D^2}{\partial y} =0 \qquad (21) </math> | ||
Na representação de fluxo de cargas as expressões (20) e (21) são apresentadas respectivamente como: | |||
<math> \frac{\partial M}{\partial t} + \frac{\partial }{\partial x}\Big(\frac{M^{2}}{D}\Big) + \frac{\partial }{\partial y}\Big(\frac{MN}{D}\Big)+ gD \frac{\partial \eta}{\partial x} = 0 \qquad (22) </math> | |||
<math> \frac{\partial | <math> \frac{\partial N}{\partial t} + \frac{\partial }{\partial y}\Big(\frac{N^{2}}{D}\Big) + \frac{\partial }{\partial x}\Big(\frac{MN}{D}\Big) +gD \frac{\partial \eta}{\partial x} = 0 \qquad (23) </math> | ||
Com as equações de águas rasas (20), (21), (22) e (23) podemos calcular as taxas de variação dos fluxos de descarga em relação ao tempo. As equações (11), (20) e (21), na representação de velocidades, e as equações (14), (22) e (23), na representação do fluxo de descargas, são as equações de águas rasas conservativas. | |||
Iremos | Iremos buscar pelas equações de águas rasas não conservativas considerando o tensor de estresse <math> \boldsymbol{\tau} </math> em (4). Os elementos deste tensor são responsáveis por causar nas partículas tensões tangenciais e perpendiculares, onde as tensões tangenciais são representadas por elementos <math> \tau_{ij}</math> onde <math> i \ne j </math>, e as perpendiculares por elementos <math> \tau_{ij}</math> onde <math> i = j </math>. | ||
Decompondo nas componentes x,y, e z de <math> \frac{1}{\rho} \nabla . \boldsymbol{\tau} </math> presente em ( | Decompondo nas componentes x,y, e z de <math> \frac{1}{\rho} \nabla . \boldsymbol{\tau} </math> presente em (4) temos: | ||
<math> \frac{1}{\rho}\Big(\frac{\partial}{\partial x} \tau_{xx} + \frac{\partial}{\partial y} \tau_{xy} + \frac{\partial}{\partial z}\tau_{xz} \Big) \qquad ( | <math> \frac{1}{\rho}\Big(\frac{\partial}{\partial x} \tau_{xx} + \frac{\partial}{\partial y} \tau_{xy} + \frac{\partial}{\partial z}\tau_{xz} \Big) \qquad (24) </math> | ||
<math> \frac{1}{\rho}\Big(\frac{\partial}{\partial x} \tau_{yx} + \frac{\partial}{\partial y} \tau_{yy} + \frac{\partial}{\partial z}\tau_{yz} \Big) \qquad ( | <math> \frac{1}{\rho}\Big(\frac{\partial}{\partial x} \tau_{yx} + \frac{\partial}{\partial y} \tau_{yy} + \frac{\partial}{\partial z}\tau_{yz} \Big) \qquad (25) </math> | ||
<math> \frac{1}{\rho}\Big(\frac{\partial}{\partial x} \tau_{zx} + \frac{\partial}{\partial y} \tau_{zy} + \frac{\partial}{\partial z}\tau_{zz} \Big) \qquad ( | <math> \frac{1}{\rho}\Big(\frac{\partial}{\partial x} \tau_{zx} + \frac{\partial}{\partial y} \tau_{zy} + \frac{\partial}{\partial z}\tau_{zz} \Big) \qquad (26) </math> | ||
Considerando o fluído Newtoniano, então as tensões de cisalhamento serão proporcionais a uma taxa de deformação, onde a constante de deformidade é a viscosidade. | Considerando o fluído Newtoniano, então as tensões de cisalhamento serão proporcionais a uma taxa de deformação, onde a constante de deformidade é a viscosidade. | ||
<math> \tau_{xy} = \tau_{yx} = \mu \Big( \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \Big) \qquad ( | <math> \tau_{xy} = \tau_{yx} = \mu \Big( \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \Big) \qquad (27) </math> | ||
<math> \tau_{xz} = \tau_{zx} = \mu \Big( \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} \Big) \qquad ( | <math> \tau_{xz} = \tau_{zx} = \mu \Big( \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} \Big) \qquad (28) </math> | ||
<math> \tau_{yz} = \tau_{zy} = \mu \Big( \frac{\partial w}{\partial y} + \frac{\partial v}{\partial z} \Big) \qquad ( | <math> \tau_{yz} = \tau_{zy} = \mu \Big( \frac{\partial w}{\partial y} + \frac{\partial v}{\partial z} \Big) \qquad (29) </math> | ||
Substituindo ( | Substituindo (27),(28) em (24), integrando em relação a componente z, utilizando a regra de Leibnz e as condições de contorno (5) e (6), obtemos: | ||
<math> \int_{-h}^{\eta} \frac{1}{\rho}\Big(\frac{\partial}{\partial x} \tau_{xx} + \frac{\partial}{\partial y} \tau_{xy} + \frac{\partial}{\partial z}\tau_{xz} \Big) = \frac{\tau_x}{\rho} -A \Big ( \frac{\partial^{2}}{\partial x^{2}}M \frac{\partial^{2}}{\partial x^{2}} M \Big) \qquad ( | <math> \int_{-h}^{\eta} \frac{1}{\rho}\Big(\frac{\partial}{\partial x} \tau_{xx} + \frac{\partial}{\partial y} \tau_{xy} + \frac{\partial}{\partial z}\tau_{xz} \Big) = \frac{\tau_x}{\rho} -A \Big ( \frac{\partial^{2}}{\partial x^{2}}M \frac{\partial^{2}}{\partial x^{2}} M \Big) \qquad (30) </math> | ||
Onde <math> A </math> é a constante de viscosidade turbulenta, <math> \tau_x </math> é uma força de resistividade relativa ao movimento do fluído com o fundo do oceano na direção x. Podemos | Onde <math> A </math> é a constante de viscosidade turbulenta, <math> \tau_x </math> é uma força de resistividade relativa ao movimento do fluído com o fundo do oceano na direção x. Podemos desconsiderar a constante de turbulência na situação em que não temos inclinações abrutas no fundo do mar <ref name=MANUAL> IMAMURA, Fumihiko.Tsunami Modelling Manual.Disponível em: http://www.tsunami.civil.tohoku.ac.jp/hokusai3/J/projects/manual-ver-3.1.pdf </ref>. | ||
Considerando que o fluído é uniforme, então a expressão para <math> \frac{\tau_x}{\rho} é </math> é: | Considerando que o fluído é uniforme, então a expressão para <math> \frac{\tau_x}{\rho} é </math> é: | ||
<math> \frac{\tau_x}{\rho} = \frac{fM}{2D^{2}}(M^{2}+N^{2})^{1/2} \qquad ( | <math> \frac{\tau_x}{\rho} = \frac{fM}{2D^{2}}(M^{2}+N^{2})^{1/2} \qquad (31) </math> | ||
<math> f </math> é o coeficiente de fricção, porém o coeficiente de rugosidade de Manning <math> n </math> é mais usado, alguns valores deste coeficiente são | Onde <math> f </math> é o coeficiente de fricção, porém o coeficiente de rugosidade de Manning <math> n </math> é mais usado, alguns valores deste coeficiente são | ||
<ref> LINSLEY, Ray K.; FRANZINI, Joseph B. Water Resources Engineering. </ref> | <ref> LINSLEY, Ray K.; FRANZINI, Joseph B. Water Resources Engineering. </ref>: | ||
{| border="4" cellpadding="2" | {| border="4" cellpadding="2" | ||
| Linha 187: | Linha 170: | ||
O coeficiente de fricção <math> f </math> e o de rugosidade de Meanning <math> n </math> estão relacionados por: | O coeficiente de fricção <math> f </math> e o de rugosidade de Meanning <math> n </math> estão relacionados por: | ||
<math> f = \frac{2gn^{2}}{D^{1/3}} \qquad (34) </math> | <math> f = \frac{2gn^{2}}{D^{1/3}} \qquad (32) </math> | ||
Substituindo (32) em (31) obtemos: | |||
<math> \frac{\tau_x}{\rho} = \frac{gn^{2}}{D^{7/3}} M(M^2 +N^2)^{1/2} \qquad (33) </math> | |||
Generalizando a expressão (29) para a componente y. | |||
<math> \frac{\tau_y}{\rho} = \frac{gn^{2}}{D^{7/3}} N(M^2 +N^2)^{1/2} \qquad (34) </math> | |||
Adicionando, repectivamente, (33) e (34) nas expressões (22) e (24), obtemos as equações de águas rasas considerando as forças de fricção do fundo do oceano. | |||
<math> \frac{\partial M}{\partial t} + \frac{\partial }{\partial x}\Big(\frac{M^{2}}{D}\Big) + \frac{\partial }{\partial y}\Big(\frac{MN}{D}\Big)+ gD \frac{\partial \eta}{\partial x} + \frac{gn^{2}}{D^{7/3}} M(M^2 +N^2)^{1/2} = 0 \qquad (35) </math> | |||
<math> \frac{\partial N}{\partial t} + \frac{\partial }{\partial y}\Big(\frac{N^{2}}{D}\Big) + \frac{\partial }{\partial x}\Big(\frac{MN}{D}\Big) +gD \frac{\partial \eta}{\partial x} +\frac{gn^{2}}{D^{7/3}} N(M^2 +N^2)^{1/2} = 0 \qquad (36) </math> | |||
As equações (14), (35) e (36), na representação do fluxo de descargas, são as equações de águas rasas não conservativas. | |||
Em uma dimensão podemos expressar as equações de águas rasas eliminando a componente <math> y</math> das expressões (14),(35) e tomando o fluxo de descarga <math> N </math> como nulo. | |||
<math>\frac{\partial \eta}{\partial t} + \frac{\partial M}{\partial x} = 0 \qquad (37) </math> | |||
<math> \frac{\ | <math> \frac{\partial M}{\partial t} + \frac{\partial }{\partial x}\Big(\frac{M^{2}}{D}\Big) + gD \frac{\partial \eta}{\partial x} +\frac{gn^{2}}{D^{7/3}} M^2= 0 \qquad (38) </math> | ||
===Simplificação das Equações de Águas Rasas=== | |||
As equações de águas rasas podem ser simplificadas para equação de advecção através das seguintes considerações: | |||
* A velocidade do fluído é constante. | |||
* A profundidade do fundo do oceano é constante. | |||
De (39) e das considerações acima temos: | |||
=== Forma Conservativa === | <math>\frac{\partial \eta}{\partial t} + \frac{\partial M}{\partial x} = \frac{\partial \eta}{\partial t} + \frac{\partial uD}{\partial x} = \frac{\partial \eta}{\partial t} +u\frac{\partial (\eta + h)}{\partial x} = \frac{\partial \eta}{\partial t} + u\frac{\partial \eta}{\partial x} = 0 </math> | ||
<math> \Rightarrow \frac{\partial \eta}{\partial t} + u\frac{\partial \eta}{\partial x} = 0 \qquad (39) </math> | |||
=== Discretização na Forma Conservativa === | |||
Um modelo mais simples - desconsiderando a fricção, viscosidade do líquido e as forças de Coriolis sobre ele - pode ser obtido <ref>GARCÍA-NAVARRO, P; et al. The shallow water equations: An example of hyperbolic system. Espanha: 2008. Disponível em: <https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.571.1364&rep=rep1&type=pdf></ref><ref>KUHBACHER, Christian. Shallow Water: Derivation and Applications. Disponível em: <http://www.mathematik.tu-dortmund.de/lsiii/cms/papers/Kuehbacher2009.pdf></ref>. Para desenvolvê-lo são necessárias algumas premissas: | Um modelo mais simples - desconsiderando a fricção, viscosidade do líquido e as forças de Coriolis sobre ele - pode ser obtido <ref>GARCÍA-NAVARRO, P; et al. The shallow water equations: An example of hyperbolic system. Espanha: 2008. Disponível em: <https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.571.1364&rep=rep1&type=pdf></ref><ref>KUHBACHER, Christian. Shallow Water: Derivation and Applications. Disponível em: <http://www.mathematik.tu-dortmund.de/lsiii/cms/papers/Kuehbacher2009.pdf></ref>. Para desenvolvê-lo são necessárias algumas premissas: | ||
| Linha 212: | Linha 217: | ||
O sistema então pode ser descrito pelas seguintes equações: | O sistema então pode ser descrito pelas seguintes equações: | ||
<math>\dfrac{\partial | <math>\dfrac{\partial D}{\partial t} + \dfrac{\partial Du}{\partial x} + \dfrac{\partial Dv}{\partial y} = 0 \qquad (40) </math> | ||
<math>\dfrac{\partial | <math>\dfrac{\partial Du}{\partial t} + \dfrac{\partial \left (\partial Du^2 + \dfrac{1}{2}g D^2 \right)}{\partial x} + \dfrac{Duv}{\partial y} = -gD\dfrac{\partial b}{\partial x} \qquad (41) </math> | ||
<math>\dfrac{\partial | <math>\dfrac{\partial Dv}{\partial t} + \dfrac{Duv}{\partial x} + \dfrac{\partial \left ( Dv^2 + \dfrac{1}{2}g D^2 \right)}{\partial y}= -gD\dfrac{\partial b}{\partial y}\qquad (42) </math> | ||
Onde <math> | Onde <math>D</math> é a altura do fluido desde a base, <math>\vec{u}, \vec{v}</math> são as velocidades médias na direções <math>\vec{x}, \vec{y}</math>, <math>g</math> é a constante gravitacional e <math>b(x, y)</math> é função que descreve a superfície onde acontece o movimento. | ||
Para descrever numericamente as equações de águas rasas na forma conservativa foi utilizado discretização por diferenças finitas e o método pra frente no tempo e no espaço (FTCS). As equações discretizadas podem ser observadas abaixo. | Para descrever numericamente as equações de águas rasas na forma conservativa foi utilizado discretização por diferenças finitas e o método pra frente no tempo e no espaço (FTCS). As equações discretizadas podem ser observadas abaixo. | ||
<math>\dfrac{ | <math>\dfrac{D^{t + \Delta t}_{i, j} - D^{t}_{i, j}}{\Delta t} + \left [ \dfrac{(Du)^t_ {i+1,j} - (Du)^t_{i-1, j}}{2 \Delta x} \right ] + \left [ \dfrac{(Dv)^t_ {i,j+1} - (Dv)^t_{i, j-1}}{2 \Delta y} \right ] = 0 \qquad (43)</math> | ||
<math>\dfrac{ | <math>\dfrac{(Du)^{t + \Delta t}_{i, j} - (Du)^{t}_{i, j}}{\Delta t} + \left [ \dfrac{(Du^2 + \cfrac{1}{2}gh^2)^t_{i+1, j} - (Du^2 + \cfrac{1}{2}gh^2)^t_{i-1, j}}{2 \Delta x} \right ] + \left [ \dfrac{(Duv)^t_{i, j+1} - (Duv)^t_{i, j-1}}{2 \Delta y} \right ] = -g D^{t}_{i, j} b_{x. i, j} \qquad (44) </math> | ||
<math>\dfrac{( | <math>\dfrac{(Dv)^{t + \Delta t}_{i, j} - (Dv)^{t}_{i, j}}{\Delta t} + \left [ \dfrac{(Duv)^t_{i+1, j} - (Duv)^t_{i-1, j}}{2 \Delta x} \right ] + \left [ \dfrac{(Dv^2 + 1/2 gD^2)^t_{i, j+1} - (Dv^2 + 1/2 gD^2)^t_{i, j-1}}{2 \Delta y} \right ] = -g D^{t}_{i, j} b_{y. i, j} \qquad (45) </math> | ||
Na situação em que temos as equações de águas rasas simplificadas por (39), aplicando FTCS explícito, a evolução temporal da amplitude da onda é: | |||
<math>\eta^{t + \Delta t}_{i, j} = \eta^{t}_{i, j} - \frac{u\Delta t}{2dx} (\eta^t_ {i+1,j} - \eta^t_{i-1, j}) \qquad (46)</math> | |||
Aplicando FTCS implícito temos: | |||
<math> | <math>\eta^{t + \Delta t}_{i, j} + \frac{u\Delta t}{2dx} (\eta^{t+ \Delta t}_{i+1,j} - \eta^{t- \Delta t}_{i-1, j}) = \eta^{t}_{i, j} \qquad (47)</math> | ||
=== Discretização na Forma não Conservativa === | |||
As equações de águas rasas na forma não conservativa são dadas por (14), (35) e (36), para descrever numericamente estas equações foi utilizada discretização por diferenças finitas, onde realizamos derivadas centradas na região espacial, e para frente na região temporal (FTCS). | |||
Discretizando a expressão ( | Discretizando a expressão (14): | ||
<math> | <math> \frac{\partial \eta}{\partial t} + \frac{\partial uD}{\partial x}+ \frac{\partial vD}{\partial y} = 0 \qquad (47) </math> | ||
<math> \Rightarrow \frac{\eta(x,y,t + \Delta t) - \eta(x,y,-t)}{\Delta t} = - \frac{M(x + \Delta x,y,t) - M(x- \Delta x,y,t)}{2\Delta x} -\frac{N(x,y+ \Delta x,t) - N(x,y - \Delta y,t)}{2\Delta y} \qquad (48) </math> | |||
<math> | <math> \eta_{i,j}^{n+1} = \eta_{i,j}^{n} -\Delta t\Bigg(\frac{M_{i+1,j}^{n}-M_{i-1,j}^{n}}{2\Delta x} + \frac{N_{i,j+1}^{n}-N_{i,j-1}^{n}}{2\Delta y} \Bigg) \qquad (49) </math> | ||
Discretizando a expressão (35): | |||
<math> | <math> \Rightarrow \frac{\partial M}{\partial t} = -\Bigg( \frac{\partial }{\partial x}\Big(\frac{M^{2}}{D}\Big) + \frac{\partial }{\partial y}\Big(\frac{MN}{D}\Big)+ gD \frac{\partial \eta}{\partial x}+ \frac{gn^{2}}{D^{7/3}} M(M^2 +N^2)^{1/2} \Bigg) \qquad (50) </math> | ||
Definindo as quantidades: | |||
<math> | <math> M2 \equiv \frac{M^2(x,y,t)}{D(x,y,t)}\qquad (51) </math> | ||
<math> MN \equiv \frac{M(x,y,t)N(x,y,t)}{D(x,y,t)} \qquad (52) </math> | |||
<math> | <math> f(x,y,t) \equiv \frac{gn^{2}}{D^{7/3}} M(M^2 +N^2)^{1/2} \qquad (53) </math> | ||
Das quantidades definidas e da derivada parcial do fluxo de descarga em relação ao tempo temos o respectivo avanço temporal para M: | |||
= | <math> M_{i,j}^{n+1} = M_{i,j}^{n} -\Delta t \Bigg( \frac{M2_{i+1,j}^n-M2_{i-1,j}^n}{2 \Delta x} +\frac{(MN)_{i,j+1}^n - (MN)_{i,j-1}^n}{2 \Delta y} +gD_{i,j}^{n} \frac{\eta_{i+1,j}^{n} - \eta_{i-1,j}^{n}}{2\Delta x} +f_{i,j}^{n}\Bigg) \qquad (54) </math> | ||
Generalizando a expressão (54) para o fluxo de descarga N temos: | |||
= | <math> N_{i,j}^{n+1} = N_{i,j}^{n} -\Delta t \Bigg( \frac{N2_{i,j+1}^n-M2_{i,j-1}^n}{2\Delta y} +\frac{(MN)_{i+1,j}^n - (MN)_{i-1,j}^n}{2\Delta x} +gD_{i,j}^{n} \frac{\eta_{i+1,j}^{n} - \eta_{i-1,j}^{n}}{2\Delta y} +f_{i,j}^{n}\Bigg) \qquad (55) </math> | ||
== Simulações Computacionais == | |||
=== Forma conservativa 1D e 2D === | |||
As equações (43),(44) e (45) foram implementadas em python para descrever a evolução temporal das variáveis <math> h</math>, <math> u </math> e <math> v </math> em duas dimensões. | |||
As condições de contorno dos exemplos obedecem as expressões: | As condições de contorno dos exemplos obedecem as expressões: | ||
| Linha 285: | Linha 293: | ||
* Nos contornos de y: <math> \tfrac{\partial h}{\partial y} = 0</math>, discretizando essa derivada temos que: <math>h_{i, j(+/-)1} = h_{i, j}</math> | * Nos contornos de y: <math> \tfrac{\partial h}{\partial y} = 0</math>, discretizando essa derivada temos que: <math>h_{i, j(+/-)1} = h_{i, j}</math> | ||
Para a solução do exemplo em 1D abaixo foi utilizado o mesmo código do conservativo 2D, porém desconsiderando a contribuição da direção <math>\vec{y}</math>. | |||
==== Códigos das Equações Conservativas ==== | |||
O código 1 foi escrito na linguagem [https://www.python.org/ ''Python''] e resolve os exemplos 1 e 2 que serão apresentados abaixo. | |||
[[Código 1 - Forma Conservativa das Equações de Águas Rasas]] | |||
O código 2 foi escrito na linguagem [https://www.python.org/ ''Python''] e serve para comparar a solução numérica de (39) com a solução exata. | |||
[[Código 2 - Método FTCS explícito]] | |||
O código 3 foi escrito na linguagem [https://www.python.org/ ''Python''] e serve para comparar a solução numérica de (39) com a solução exata. | |||
[[Código 3 - Método FTCS implícito]] | |||
==== Resultados ==== | |||
'''Comparação entre a solução exata e a numérica''': para verificar se o cálculo das equações de águas rasas utilizando FTCS explícito e implícito estão funcionando, partimos da situação simplificada das equações dadas por (46) e (47). Neste problema consideramos a velocidade e a profundidade constantes com os valores respectivos de 4.3 m/s e 2 m. O deslocamento de água inicial é representado por uma Gaussiana centrada em 80m, de amplitude 2 m e largura 70 m, nesta situação a solução exata de (39) é dada por: | |||
<math> \eta = 2 + 3 \cdot exp \Big(-\frac{((x-80) -ut))^2}{70} \Big) </math> | |||
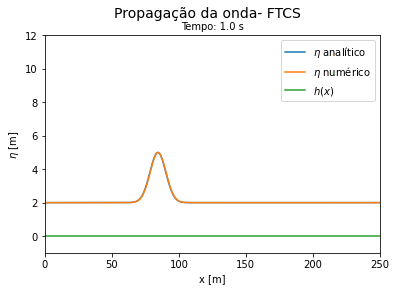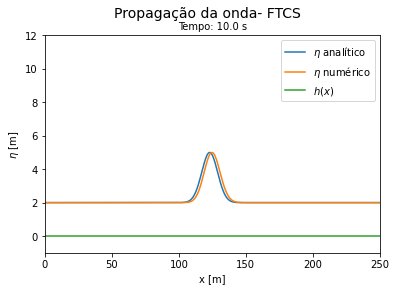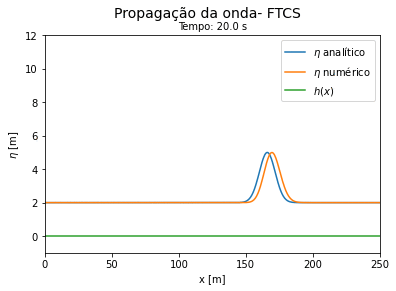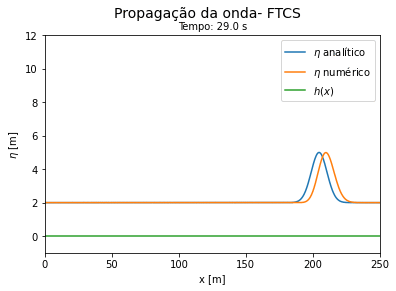
Do código 2 obtemos as seguintes curvas ao longo do tempo. Vemos que a solução numérica por FTCS explícito se aproxima do resultado exato para tempos curtos e se afasta da solução exata a medida que o tempo avança. | |||
[[Arquivo:Aguas rasas FTCS explicito.gif|thumb|400px|center|Comparação entre a solução exata e a numérica por FTCS explícito. Forma conservativa.]] | |||
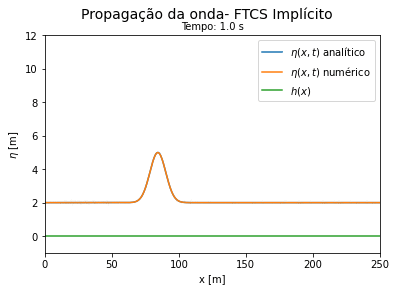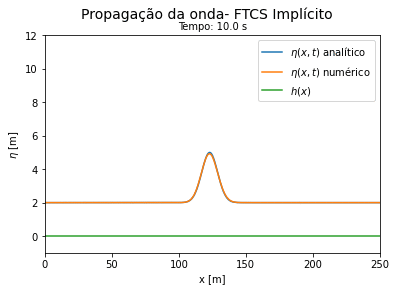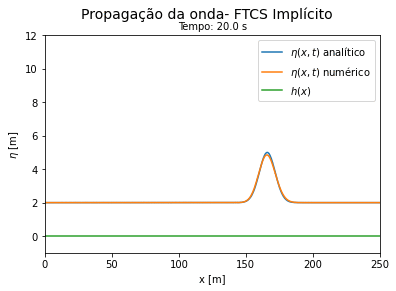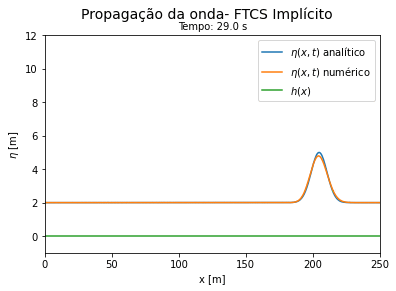
Do código 3 obtemos as seguintes curvas ao longo do tempo. Vemos que a solução numérica por FTCS implícito se aproxima do resultado analítico para tempos curtos e se afasta da solução exata a medida que o tempo avança, porém de forma mais lenta que o método explícito. | |||
[[Arquivo:Aguas rasas FTCS implicito.gif|thumb|400px|center|Comparação entre a solução exata e a numérica por FTCS implícito. Forma conservativa.]] | |||
<math> u \Delta t </math> deve ser significativamente menor que <math> \Delta x </math> para que os métodos FTCS funcionem. | |||
'''Exemplo 1. Onda confinada em uma caixa com profundidade constante''': obtemos a evolução da amplitude da onda apresentada no GIF abaixo, através do código 1, utilizando que a profundidade é constante, e que tanto a velocidade quanto altura da onda são inicialmente funções gaussianas centradas no espaço. | |||
[[Arquivo:conservativa-gausiana.gif|thumb|400px|center|Evolução da amplitude da onda em uma caixa. Forma conservativa]] | |||
Podemos observar que a onda diminui sua amplitude a medida que ela se propaga no espaço. Posteriormente, são observados fenômenos de interferência construtiva e destrutiva devido a reflexão da onda com as paredes da caixa. | |||
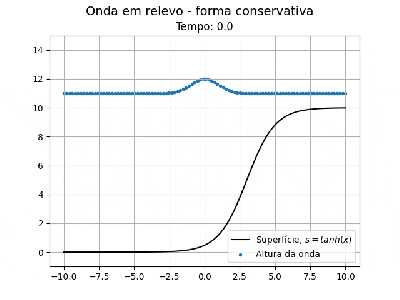
'''Exemplo 2. Onda confinada em uma caixa com profundidade variável''': utilizando a função <math>s = tanh(x)</math> foi possível simular uma onda chegando em uma praia, esse exemplo foi feito em 1D conservativo. | |||
Para fazer esse exemplo usamos o código 1, porém desconsideramos as derivadas em <math>x</math> e inicializamos os vetores da altura e velocidade com a discretização em apenas uma dimensão (abaixo descrevemos está parte do código). Deve-se notar que o problema passa a ter um índice, pois a discretização não forma mais uma malha, então pode ser retirado um laço ''for'' do código. | |||
<source lang='python'> | |||
#%% Discretização do espaço x | |||
x = np.linspace(L_x0, L_xf, NX) | |||
#%% Condições iniciais da superficie e da agua | |||
# | # Superficie | ||
b = 5 * np.tanh((x- L_xf*0.3) / 2) # funcao tangente | |||
b += np.full(shape=(np.shape(b)), fill_value=-np.min(b)) # aqui é somado só para a funcao comecar em zero | |||
# | # Onda e velocidade | ||
sigma = 1.0 # distribuicao da onda | |||
sigma_v = 1.0 # distribuicao da onda | |||
h_2d = 1.1 * max(b) * np.ones(shape=np.shape(x)) + np.exp(-((x)**2/(2*(sigma**2)))) | |||
h_2d -= b | |||
u_2d = 0.08 * np.exp(-((x)**2/(2*(sigma_v**2)))) | |||
</source> | </source> | ||
[[Arquivo:gif_conservativa_tanh.gif|thumb|400px|center|Evolução da amplitude da onda em uma caixa com profundidade variável. Forma conservativa]] | |||
[[Arquivo: | |||
=== Forma dissipativa 2D === | === Forma dissipativa 2D === | ||
Os exemplos que seguem utilizam as equações de | Os exemplos que seguem utilizam o código abaixo para calcular as equações de águas rasas não conservativa (38),(43) e (44) nos passos de tempo de <math> \eta </math>, <math> M </math>, <math> N </math>, onde as funções em python ''atualiza_eta'', ''atualiza_M'', e ''atualiza_N'' implementam computacionalmente isto. Para implementar estas funções e outras ideias do nosso programa, o seguinte código fonte da referência <ref> KOEHN, Daniel. 2D Shallow Water Equations. Disponível em: <https://github.com/daniel-koehn/Differential-equations-earth-system/blob/master/10_Shallow_Water_Equation_2D/01_2D_Shallow_Water_Equations.ipynb> </ref> foi usado como base. | ||
==== Códigos das Equações Não Conservativas ==== | |||
O código 4 foi escrito na linguagem [https://www.python.org/ ''Python''] e resolve o exemplo 3 que será apresentado abaixo. | |||
[[Código 4 - Forma Não Conservativa das Equações de Águas Rasas]] | |||
O código 5 foi escrito na linguagem [https://www.python.org/ ''Python''] e resolve o exemplo 4 que será apresentado abaixo. | |||
[[Código 5 - Forma Não Conservativa das Equações de Águas Rasas]] | |||
==== Exemplo 3 - Onda Confinada em uma Caixa ==== | |||
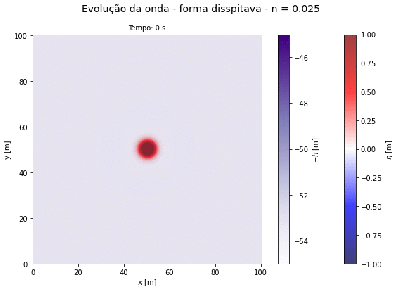
Através do código 4 fizemos a simulação da propagação de uma onda em uma caixa de <math> L_x =100 </math> m e <math> L_y = 100 </math> m em uma profundidade <math>h(x,y)=50</math> m. O fluxo de descarga e o deslocamento do volume de água inicial, ambas com suas devidas unidades físicas, são Gaussianas centradas em 80, com amplitude igual a 1 e largura igual a 70. | |||
Exemplo 3 com coeficiente de Manning igual a 0.025. | |||
[[Arquivo:Aguas rasas FTCS n=0.025.gif|thumb|400px|center|Evolução da amplitude da onda em uma caixa com profundidade de 50 metros, coeficiente de Manning n = 0.025. Forma dissipativa.]] | |||
Exemplo 3 com coeficiente de Manning igual a 20.0. | |||
[[Arquivo:Aguas rasas não conservativo n=20.gif|thumb|400px|center|Evolução da amplitude da onda em uma caixa com profundidade de 50 metros, coeficiente de Manning n = 20. Forma dissipativa.]] | |||
Dos gráficos acima, podemos observar que quanto maior for o coeficiente de Manning mais rápida a onda irá atenuar a sua amplitude. Está observação faz sentido, já que as forças de fricção sobre o fluído são maiores na situação em que o coeficiente de Manning tem maior valor. | |||
==== Exemplo | ==== Exemplo 4 - Tsunami ==== | ||
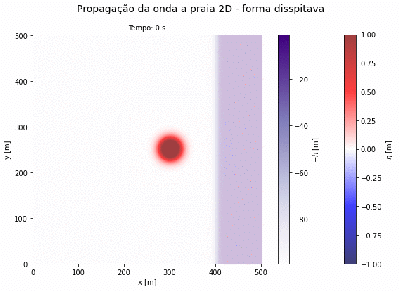
Simulação da propagação de uma onda em uma caixa de <math> L_x =500</math> <math> m </math> e <math> L_y =500 </math> <math> m </math>, em uma profundidade variável, que respeita a função tangente hiperbólica. O fluxo de descarga e o deslocamento do volume de água inicial, ambas com suas devidas unidades físicas, são Gaussianas centradas em 300, com amplitude igual a 2 e largura igual a 500. | |||
[[Arquivo:Tsunami.gif|thumb|400px|center|Evolução da amplitude da onda em uma caixa com profundidade variáel, coeficiente de Manning n = 0.025. Forma dissipativa.]] | |||
A medida que o fundo do oceano diminui sua profundidade a velocidade da onda diminui e a amplitude aumenta. Está simulação mostra o comportamento físico da propagação de um Tsunami em direção ao litoral. | |||
== Comparação entre Métodos == | == Comparação entre Métodos == | ||
| Linha 693: | Linha 398: | ||
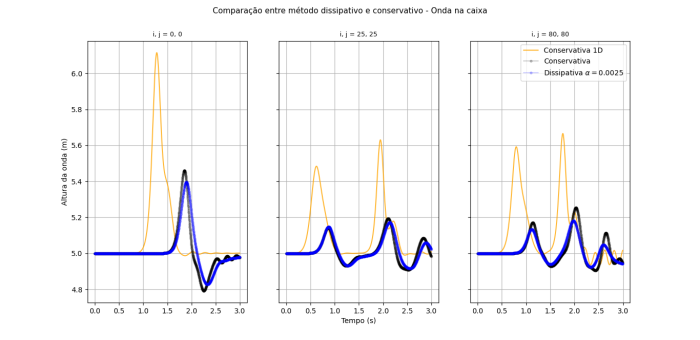
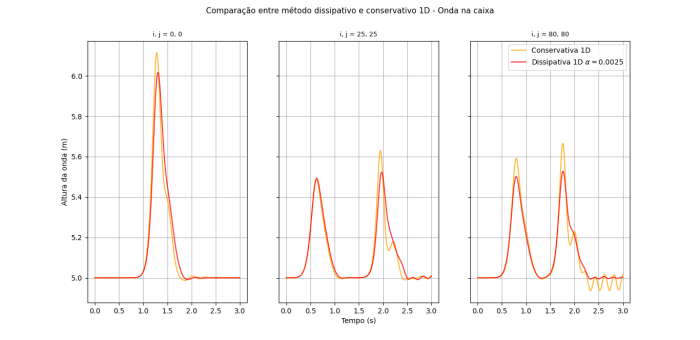
=== Onda confinada em uma caixa === | === Onda confinada em uma caixa === | ||
Abaixo é mostrado o gráfico de evolução temporal da altura da onda em três pontos distintos do sistema. Pode-se perceber que com o passar do tempo o movimento das duas equações começa a divergir, mesmo com o fator de fricção baixo. | Abaixo é mostrado o gráfico de evolução temporal da altura da onda em três pontos distintos do sistema (utilizando os mesmos parâmetros que foi aplicado ao método conservativo com a onda em uma caixa de profundidade constante em todos os outros métodos). Pode-se perceber que com o passar do tempo o movimento das duas equações começa a divergir, mesmo com o fator de fricção baixo. | ||
| Linha 702: | Linha 407: | ||
[[Arquivo:unificacao_comparacoes_1D.png|thumb|center|700px|Comparação da evolução temporal da altura da onda nos métodos conservativo e dissipativo 2D e conservativo 1D]] | [[Arquivo:unificacao_comparacoes_1D.png|thumb|center|700px|Comparação da evolução temporal da altura da onda nos métodos conservativo e dissipativo 2D e conservativo 1D]] | ||
Também é possível perceber a diferença entre métodos observando apenas em uma direção (<math>\vec{x}</math>). | Também é possível perceber a diferença entre métodos observando apenas em uma direção (<math>\vec{x}</math>), por causa dos termos de fricção e viscosidade. | ||
[[Arquivo:unificacao_comparacoes_1D_mesmo.png|thumb|center|700px|Comparação da evolução temporal da altura da onda nos métodos conservativo e dissipativo 1D]] | [[Arquivo:unificacao_comparacoes_1D_mesmo.png|thumb|center|700px|Comparação da evolução temporal da altura da onda nos métodos conservativo e dissipativo 1D]] | ||
Edição atual tal como às 22h03min de 21 de outubro de 2021
Grupo: Gabriel Schmökel e Julia Remus
O objetivo deste trabalho é buscar a solução das equações de águas rasas, por meio de métodos de integração numérica, para resolução de equações diferenciais parciais (EDP's) e posteriormente apresentar uma breve interpretação física das soluções. Demonstramos, nesta página, a derivação das equações, junto com a explicação de cada quantidade física presente. A discretização das equações de águas rasas conservativas e não conservativas são feitas por FTCS explícito, também foi aplicado FTCS implícito para as equações em uma forma simplificada, representada pela equação da deriva. Os resultados obtidos para equação simplificada são comparados com a solução exata, e exemplos mais complexos são solucionados para as formas conservativa e não conservativa. Ao final, uma comparação é feita entre os resultados das equações conservativas e dissipativas.
Introdução
As equações de águas rasas têm aplicações físicas na previsão de tsunâmis, em fluxos atmosféricos, ondas de tempestade e fluxos planetários. Na descrição física dos problemas de fluxos de fluído em ondas, as equações de águas rasas em uma dimensão são dadas por:
As componentes da equação de águas rasas podem ser melhor interpretadas através da seguinte figura:
corresponde a amplitude da onda, determina a profundidade do mar em repouso, é o deslocamento total da água, é a velocidade do fluído. Resolvendo a EDP da equação de águas rasas, obtemos como a amplitude da onda se comporta ao longo do tempo e do espaço.
Teoria
Derivação das Equações de Águas Rasas
Iremos demonstrar como chegamos nas equações de águas rasas em duas dimensões, nas formas conservativa e dissipativa, em representações do fluxo de descarga e de velocidade. Posteriormente, tendo as equações em 2D, iremos simplificar elas para a forma unidimensional. Neste processo de demonstração, iremos explicar a interpretação física de cada quantidade presente nas equações.
Para obter as equações de águas rasas devemos partir da equação da continuidade e das equações da quantidade de movimento de Navier-Stokes:
A equação da continuidade em (3) descreve o balanço de massas para os elementos de volume infinitesimais que pertencem ao fluído, onde a quantidade do lado esquerdo da equação informa o fluxo de massa que entra e sai pelo elemento de volume, e a quantidade do lado direito está relacionada com a massa que se acumula ao longo do tempo [1]. Nesta expressão é a densidade, e é o campo de velocidades, onde u,v e w são as velocidades das partículas que compõe o fluído nas direções x,y,z.
As equações de Navier-Stokes em (4) são balanços diferenciais da quantidade de movimento, obtidas através da aplicação da segunda lei de Newton em cada ponto do escoamento [2] [3] [4].
- é a aceleração da partícula fluída ao longo do campo de velocidade .
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla . \boldsymbol{\tau} / \rho} está associado as tensões tangenciais e normais atuando sobre os elementos de volume (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\tau} } é o tensor tensão, as componentes deste tensor são as tensões normais e tangenciais de cisalhamento, expressas por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_{ij} } , no qual Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } indica a direção e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j } o plano normal).
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla p / \rho } está associado as pressões que atuam sobre os elementos do fluído.
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{g} } é o vetor aceleração da gravidade atuando sobre os elementos infinitesimais de volume do fluído.
Introduzindo as condições de contorno para a superfície Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z(x,y,t) } e para a profundidade do oceano Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle h(x,y) } [5]:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{D \eta}{Dt} = \frac{\partial \eta}{\partial t} +\mathbf{v} . \nabla \eta = w } , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z= \eta(x,y,t) \qquad (5) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{u} . \nabla (z + h(x,y)) = 0 } , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z =-h(x,y) \qquad (6)}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta } é o deslocamento vertical da água sobre a superfície em repouso, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v} = (x,y,0) } é o vetor velocidade do fluído nas direções horizontais x e y.
A equação da continuidade em (3) pode ser simplificada pelo fato do fluído ser incompressível, isto implica que a densidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho } é constante.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla . \mathbf{u} = 0 \qquad (7) }
Integrando a expressão da continuidade em (7), utilizando a regra da integral de Leibniz [6], com os limites indo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -h(x,y) } até Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta (x,y,t) } chegamos na seguinte expressão:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-h}^{\eta} \nabla . \mathbf{u} = \int_{-h}^{\eta} \Big(\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z}\Big)dz = \frac{\partial}{\partial x} \int_{-h}^{\eta} u dz + \frac{\partial}{\partial y} \int_{-h}^{\eta} v dz +w \Big |_{-h}^{\eta} + \mathbf{u} . \nabla (z + h(x,y)) \Big |_{-h}^{\eta} -u \Big |_{-h}^{\eta} \frac{\partial \eta}{\partial x} -v \Big |_{-h}^{\eta} \frac{\partial \eta}{\partial y} \qquad (8) }
Teorema de Leibniz:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d}{dx} \left (\int_{a(x)}^{b(x)} f(x,t)\,dt \right )= f\big(x,b(x)\big)\cdot \frac{d}{dx} b(x) - f\big(x,a(x)\big)\cdot \frac{d}{dx} a(x) + \int_{a(x)}^{b(x)}\frac{\partial}{\partial x} f(x,t) \,dt \qquad (9)}
Substituindo as condições de contorno da profundidade (6) em (8) obtemos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial x} \int_{-h}^{\eta} u dz + \frac{\partial}{\partial y} \int_{-h}^{\eta} v dz - w \Big |_{eta} -\mathbf{v} . \nabla \eta = 0 \qquad (10) }
Substituindo a condição de contorno da superfície (5) em (10):
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial x} \int_{-h}^{\eta} u dz + \frac{\partial}{\partial y} \int_{-h}^{\eta} v dz + \frac{\partial \eta}{\partial t} = \frac{\partial u (\eta + h)}{\partial x}+ \frac{\partial v (\eta + h)}{\partial y} + \frac{\partial \eta}{\partial t} = \frac{\partial uD}{\partial x}+ \frac{\partial vD}{\partial y} + \frac{\partial \eta}{\partial t} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \frac{\partial \eta}{\partial t} + \frac{\partial uD}{\partial x}+ \frac{\partial vD}{\partial y} = 0 \qquad (11) }
(11) é a primeira das equações das águas rasas que obtemos, onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D } é o comprimento da água total do fundo do oceano até a amplitude da onda. Podemos expressar (11) através do fluxo de descarga nas direções x e y, estas quantidades estão relacionadas com as velocidades da seguinte forma [7]:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle M = \frac{\partial}{\partial x} \int_{-h}^{\eta} u dz = uD \qquad (12) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = \frac{\partial}{\partial y} \int_{-h}^{\eta} v dz = vD \qquad (13) }
Substituindo (12) e (13) em (11) chegamos na representação do fluxo de descarga para uma das equações de águas rasas.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \frac{\partial \eta}{\partial t} + \frac{\partial M}{\partial x}+ \frac{\partial N}{\partial y} = 0 \qquad (14) }
Conhecendo as taxas dos fluxos de descarga em relação as regiões espaciais, podemos determinar a taxa da variação da amplitude da onda em relação ao tempo.
Vamos buscar obter as outras duas equações de águas rasas restantes, a partir das quantidades de movimento de Navier-Stokes. Nas componentes x,y e z temos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} +\frac{1}{\rho}\frac{\partial P}{\partial x} +g_x = 0 \qquad (15) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z} +\frac{1}{\rho}\frac{\partial P}{\partial x} +g_y = 0 \qquad (16) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\rho}\frac{\partial P}{\partial x} +g_z = 0 \qquad (17) }
Na componente z em (17) não consideramos a aceleração das partículas, pois a aceleração da gravidade é muito maior. Também tomamos como nulo as componentes Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_x} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_y} em (15) e (16), assim passamos a definir Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_z = g } . Neste momento estamos desconsiderando as forças de fricção, por isso o tensor tensão também é nulo.
Resolvendo equação diferencial da componente z em (17) podemos obter a pressão, a qual é hidrostática.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \partial P = \rho g \partial z \Rightarrow P = \rho g (\eta - z) \qquad (18) }
Substituindo a pressão em (15):
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} +g \frac{\partial \eta}{\partial x} =0 \qquad (19) }
Integrando a expressão (19), utilizando a regra da integral de Leibniz e as condições de contorno (5) e (6), com os limites indo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -h(x,y)} até Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta(x,y,t)} chegamos em outra das equações de águas rasas:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial uD}{\partial t} + \frac{\partial u^{2}D}{\partial x} + \frac{\partial uvD}{\partial y} + \frac{g}{2} \frac{\partial D^2}{\partial x} =0 \qquad (20) }
Generalizando a equação (20), para a componente y, obtemos a última das equações de águas rasas:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial vD}{\partial t} + \frac{\partial v^{2}D}{\partial y} + \frac{\partial uvD}{\partial x} + \frac{g}{2} \frac{\partial D^2}{\partial y} =0 \qquad (21) }
Na representação de fluxo de cargas as expressões (20) e (21) são apresentadas respectivamente como:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial M}{\partial t} + \frac{\partial }{\partial x}\Big(\frac{M^{2}}{D}\Big) + \frac{\partial }{\partial y}\Big(\frac{MN}{D}\Big)+ gD \frac{\partial \eta}{\partial x} = 0 \qquad (22) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial N}{\partial t} + \frac{\partial }{\partial y}\Big(\frac{N^{2}}{D}\Big) + \frac{\partial }{\partial x}\Big(\frac{MN}{D}\Big) +gD \frac{\partial \eta}{\partial x} = 0 \qquad (23) }
Com as equações de águas rasas (20), (21), (22) e (23) podemos calcular as taxas de variação dos fluxos de descarga em relação ao tempo. As equações (11), (20) e (21), na representação de velocidades, e as equações (14), (22) e (23), na representação do fluxo de descargas, são as equações de águas rasas conservativas.
Iremos buscar pelas equações de águas rasas não conservativas considerando o tensor de estresse Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\tau} } em (4). Os elementos deste tensor são responsáveis por causar nas partículas tensões tangenciais e perpendiculares, onde as tensões tangenciais são representadas por elementos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_{ij}} onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \ne j } , e as perpendiculares por elementos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_{ij}} onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = j } .
Decompondo nas componentes x,y, e z de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\rho} \nabla . \boldsymbol{\tau} } presente em (4) temos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\rho}\Big(\frac{\partial}{\partial x} \tau_{xx} + \frac{\partial}{\partial y} \tau_{xy} + \frac{\partial}{\partial z}\tau_{xz} \Big) \qquad (24) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\rho}\Big(\frac{\partial}{\partial x} \tau_{yx} + \frac{\partial}{\partial y} \tau_{yy} + \frac{\partial}{\partial z}\tau_{yz} \Big) \qquad (25) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\rho}\Big(\frac{\partial}{\partial x} \tau_{zx} + \frac{\partial}{\partial y} \tau_{zy} + \frac{\partial}{\partial z}\tau_{zz} \Big) \qquad (26) }
Considerando o fluído Newtoniano, então as tensões de cisalhamento serão proporcionais a uma taxa de deformação, onde a constante de deformidade é a viscosidade.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_{xy} = \tau_{yx} = \mu \Big( \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \Big) \qquad (27) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_{xz} = \tau_{zx} = \mu \Big( \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} \Big) \qquad (28) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_{yz} = \tau_{zy} = \mu \Big( \frac{\partial w}{\partial y} + \frac{\partial v}{\partial z} \Big) \qquad (29) }
Substituindo (27),(28) em (24), integrando em relação a componente z, utilizando a regra de Leibnz e as condições de contorno (5) e (6), obtemos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-h}^{\eta} \frac{1}{\rho}\Big(\frac{\partial}{\partial x} \tau_{xx} + \frac{\partial}{\partial y} \tau_{xy} + \frac{\partial}{\partial z}\tau_{xz} \Big) = \frac{\tau_x}{\rho} -A \Big ( \frac{\partial^{2}}{\partial x^{2}}M \frac{\partial^{2}}{\partial x^{2}} M \Big) \qquad (30) }
Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A } é a constante de viscosidade turbulenta, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_x } é uma força de resistividade relativa ao movimento do fluído com o fundo do oceano na direção x. Podemos desconsiderar a constante de turbulência na situação em que não temos inclinações abrutas no fundo do mar [7].
Considerando que o fluído é uniforme, então a expressão para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\tau_x}{\rho} é } é:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\tau_x}{\rho} = \frac{fM}{2D^{2}}(M^{2}+N^{2})^{1/2} \qquad (31) }
Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f } é o coeficiente de fricção, porém o coeficiente de rugosidade de Manning Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n } é mais usado, alguns valores deste coeficiente são [8]:
| Material | Coeficiente de Rugosidade de Manning Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (n) } |
|---|---|
| Cimento puro e metal liso | 0,010 |
| Terra lisa | 0,017 |
| Pedras, ervas daninhas | 0,035 |
| Péssimo relevo de canal | 0,060 |
| Bom relevo de canal | 0,025 |
O coeficiente de fricção Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f } e o de rugosidade de Meanning Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n } estão relacionados por:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f = \frac{2gn^{2}}{D^{1/3}} \qquad (32) }
Substituindo (32) em (31) obtemos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\tau_x}{\rho} = \frac{gn^{2}}{D^{7/3}} M(M^2 +N^2)^{1/2} \qquad (33) }
Generalizando a expressão (29) para a componente y.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\tau_y}{\rho} = \frac{gn^{2}}{D^{7/3}} N(M^2 +N^2)^{1/2} \qquad (34) }
Adicionando, repectivamente, (33) e (34) nas expressões (22) e (24), obtemos as equações de águas rasas considerando as forças de fricção do fundo do oceano.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial M}{\partial t} + \frac{\partial }{\partial x}\Big(\frac{M^{2}}{D}\Big) + \frac{\partial }{\partial y}\Big(\frac{MN}{D}\Big)+ gD \frac{\partial \eta}{\partial x} + \frac{gn^{2}}{D^{7/3}} M(M^2 +N^2)^{1/2} = 0 \qquad (35) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial N}{\partial t} + \frac{\partial }{\partial y}\Big(\frac{N^{2}}{D}\Big) + \frac{\partial }{\partial x}\Big(\frac{MN}{D}\Big) +gD \frac{\partial \eta}{\partial x} +\frac{gn^{2}}{D^{7/3}} N(M^2 +N^2)^{1/2} = 0 \qquad (36) }
As equações (14), (35) e (36), na representação do fluxo de descargas, são as equações de águas rasas não conservativas.
Em uma dimensão podemos expressar as equações de águas rasas eliminando a componente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} das expressões (14),(35) e tomando o fluxo de descarga Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } como nulo.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial \eta}{\partial t} + \frac{\partial M}{\partial x} = 0 \qquad (37) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial M}{\partial t} + \frac{\partial }{\partial x}\Big(\frac{M^{2}}{D}\Big) + gD \frac{\partial \eta}{\partial x} +\frac{gn^{2}}{D^{7/3}} M^2= 0 \qquad (38) }
Simplificação das Equações de Águas Rasas
As equações de águas rasas podem ser simplificadas para equação de advecção através das seguintes considerações:
- A velocidade do fluído é constante.
- A profundidade do fundo do oceano é constante.
De (39) e das considerações acima temos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial \eta}{\partial t} + \frac{\partial M}{\partial x} = \frac{\partial \eta}{\partial t} + \frac{\partial uD}{\partial x} = \frac{\partial \eta}{\partial t} +u\frac{\partial (\eta + h)}{\partial x} = \frac{\partial \eta}{\partial t} + u\frac{\partial \eta}{\partial x} = 0 }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \frac{\partial \eta}{\partial t} + u\frac{\partial \eta}{\partial x} = 0 \qquad (39) }
Discretização na Forma Conservativa
Um modelo mais simples - desconsiderando a fricção, viscosidade do líquido e as forças de Coriolis sobre ele - pode ser obtido [9][10]. Para desenvolvê-lo são necessárias algumas premissas:
- O comprimento da onda é muito maior que as contribuições na direção Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{z}}
- A aceleração na direção da velocidade na direção Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{z}} é zero
- As componentes das velocidades em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{x}} e em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{y}} (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{u}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v}} ) não variam em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{z}}
O sistema então pode ser descrito pelas seguintes equações:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{\partial D}{\partial t} + \dfrac{\partial Du}{\partial x} + \dfrac{\partial Dv}{\partial y} = 0 \qquad (40) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{\partial Du}{\partial t} + \dfrac{\partial \left (\partial Du^2 + \dfrac{1}{2}g D^2 \right)}{\partial x} + \dfrac{Duv}{\partial y} = -gD\dfrac{\partial b}{\partial x} \qquad (41) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{\partial Dv}{\partial t} + \dfrac{Duv}{\partial x} + \dfrac{\partial \left ( Dv^2 + \dfrac{1}{2}g D^2 \right)}{\partial y}= -gD\dfrac{\partial b}{\partial y}\qquad (42) }
Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} é a altura do fluido desde a base, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{u}, \vec{v}} são as velocidades médias na direções Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{x}, \vec{y}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} é a constante gravitacional e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle b(x, y)} é função que descreve a superfície onde acontece o movimento.
Para descrever numericamente as equações de águas rasas na forma conservativa foi utilizado discretização por diferenças finitas e o método pra frente no tempo e no espaço (FTCS). As equações discretizadas podem ser observadas abaixo.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{D^{t + \Delta t}_{i, j} - D^{t}_{i, j}}{\Delta t} + \left [ \dfrac{(Du)^t_ {i+1,j} - (Du)^t_{i-1, j}}{2 \Delta x} \right ] + \left [ \dfrac{(Dv)^t_ {i,j+1} - (Dv)^t_{i, j-1}}{2 \Delta y} \right ] = 0 \qquad (43)}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{(Du)^{t + \Delta t}_{i, j} - (Du)^{t}_{i, j}}{\Delta t} + \left [ \dfrac{(Du^2 + \cfrac{1}{2}gh^2)^t_{i+1, j} - (Du^2 + \cfrac{1}{2}gh^2)^t_{i-1, j}}{2 \Delta x} \right ] + \left [ \dfrac{(Duv)^t_{i, j+1} - (Duv)^t_{i, j-1}}{2 \Delta y} \right ] = -g D^{t}_{i, j} b_{x. i, j} \qquad (44) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{(Dv)^{t + \Delta t}_{i, j} - (Dv)^{t}_{i, j}}{\Delta t} + \left [ \dfrac{(Duv)^t_{i+1, j} - (Duv)^t_{i-1, j}}{2 \Delta x} \right ] + \left [ \dfrac{(Dv^2 + 1/2 gD^2)^t_{i, j+1} - (Dv^2 + 1/2 gD^2)^t_{i, j-1}}{2 \Delta y} \right ] = -g D^{t}_{i, j} b_{y. i, j} \qquad (45) }
Na situação em que temos as equações de águas rasas simplificadas por (39), aplicando FTCS explícito, a evolução temporal da amplitude da onda é:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta^{t + \Delta t}_{i, j} = \eta^{t}_{i, j} - \frac{u\Delta t}{2dx} (\eta^t_ {i+1,j} - \eta^t_{i-1, j}) \qquad (46)}
Aplicando FTCS implícito temos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta^{t + \Delta t}_{i, j} + \frac{u\Delta t}{2dx} (\eta^{t+ \Delta t}_{i+1,j} - \eta^{t- \Delta t}_{i-1, j}) = \eta^{t}_{i, j} \qquad (47)}
Discretização na Forma não Conservativa
As equações de águas rasas na forma não conservativa são dadas por (14), (35) e (36), para descrever numericamente estas equações foi utilizada discretização por diferenças finitas, onde realizamos derivadas centradas na região espacial, e para frente na região temporal (FTCS).
Discretizando a expressão (14):
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial \eta}{\partial t} + \frac{\partial uD}{\partial x}+ \frac{\partial vD}{\partial y} = 0 \qquad (47) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \frac{\eta(x,y,t + \Delta t) - \eta(x,y,-t)}{\Delta t} = - \frac{M(x + \Delta x,y,t) - M(x- \Delta x,y,t)}{2\Delta x} -\frac{N(x,y+ \Delta x,t) - N(x,y - \Delta y,t)}{2\Delta y} \qquad (48) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta_{i,j}^{n+1} = \eta_{i,j}^{n} -\Delta t\Bigg(\frac{M_{i+1,j}^{n}-M_{i-1,j}^{n}}{2\Delta x} + \frac{N_{i,j+1}^{n}-N_{i,j-1}^{n}}{2\Delta y} \Bigg) \qquad (49) }
Discretizando a expressão (35):
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \frac{\partial M}{\partial t} = -\Bigg( \frac{\partial }{\partial x}\Big(\frac{M^{2}}{D}\Big) + \frac{\partial }{\partial y}\Big(\frac{MN}{D}\Big)+ gD \frac{\partial \eta}{\partial x}+ \frac{gn^{2}}{D^{7/3}} M(M^2 +N^2)^{1/2} \Bigg) \qquad (50) }
Definindo as quantidades:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle M2 \equiv \frac{M^2(x,y,t)}{D(x,y,t)}\qquad (51) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle MN \equiv \frac{M(x,y,t)N(x,y,t)}{D(x,y,t)} \qquad (52) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x,y,t) \equiv \frac{gn^{2}}{D^{7/3}} M(M^2 +N^2)^{1/2} \qquad (53) }
Das quantidades definidas e da derivada parcial do fluxo de descarga em relação ao tempo temos o respectivo avanço temporal para M:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{i,j}^{n+1} = M_{i,j}^{n} -\Delta t \Bigg( \frac{M2_{i+1,j}^n-M2_{i-1,j}^n}{2 \Delta x} +\frac{(MN)_{i,j+1}^n - (MN)_{i,j-1}^n}{2 \Delta y} +gD_{i,j}^{n} \frac{\eta_{i+1,j}^{n} - \eta_{i-1,j}^{n}}{2\Delta x} +f_{i,j}^{n}\Bigg) \qquad (54) }
Generalizando a expressão (54) para o fluxo de descarga N temos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_{i,j}^{n+1} = N_{i,j}^{n} -\Delta t \Bigg( \frac{N2_{i,j+1}^n-M2_{i,j-1}^n}{2\Delta y} +\frac{(MN)_{i+1,j}^n - (MN)_{i-1,j}^n}{2\Delta x} +gD_{i,j}^{n} \frac{\eta_{i+1,j}^{n} - \eta_{i-1,j}^{n}}{2\Delta y} +f_{i,j}^{n}\Bigg) \qquad (55) }
Simulações Computacionais
Forma conservativa 1D e 2D
As equações (43),(44) e (45) foram implementadas em python para descrever a evolução temporal das variáveis Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v } em duas dimensões.
As condições de contorno dos exemplos obedecem as expressões:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(x_f, y) = - u(x_f - \Delta x, y)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(x_i, y) = - u(x_i + \Delta x, y)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v(x, y_f) = - v(x, y_f - \Delta y)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v(x, y_i) = - v(x, y_i + \Delta y)}
- Nos contornos de x: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{\partial h}{\partial x} = 0} , discretizando essa derivada temos que: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_{i(+/-)1, j} = h_{i, j}}
- Nos contornos de y: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{\partial h}{\partial y} = 0} , discretizando essa derivada temos que: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_{i, j(+/-)1} = h_{i, j}}
Para a solução do exemplo em 1D abaixo foi utilizado o mesmo código do conservativo 2D, porém desconsiderando a contribuição da direção Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{y}} .
Códigos das Equações Conservativas
O código 1 foi escrito na linguagem Python e resolve os exemplos 1 e 2 que serão apresentados abaixo.
Código 1 - Forma Conservativa das Equações de Águas Rasas
O código 2 foi escrito na linguagem Python e serve para comparar a solução numérica de (39) com a solução exata.
Código 2 - Método FTCS explícito
O código 3 foi escrito na linguagem Python e serve para comparar a solução numérica de (39) com a solução exata.
Código 3 - Método FTCS implícito
Resultados
Comparação entre a solução exata e a numérica: para verificar se o cálculo das equações de águas rasas utilizando FTCS explícito e implícito estão funcionando, partimos da situação simplificada das equações dadas por (46) e (47). Neste problema consideramos a velocidade e a profundidade constantes com os valores respectivos de 4.3 m/s e 2 m. O deslocamento de água inicial é representado por uma Gaussiana centrada em 80m, de amplitude 2 m e largura 70 m, nesta situação a solução exata de (39) é dada por:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta = 2 + 3 \cdot exp \Big(-\frac{((x-80) -ut))^2}{70} \Big) }
Do código 2 obtemos as seguintes curvas ao longo do tempo. Vemos que a solução numérica por FTCS explícito se aproxima do resultado exato para tempos curtos e se afasta da solução exata a medida que o tempo avança.
Do código 3 obtemos as seguintes curvas ao longo do tempo. Vemos que a solução numérica por FTCS implícito se aproxima do resultado analítico para tempos curtos e se afasta da solução exata a medida que o tempo avança, porém de forma mais lenta que o método explícito.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u \Delta t } deve ser significativamente menor que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x } para que os métodos FTCS funcionem.
Exemplo 1. Onda confinada em uma caixa com profundidade constante: obtemos a evolução da amplitude da onda apresentada no GIF abaixo, através do código 1, utilizando que a profundidade é constante, e que tanto a velocidade quanto altura da onda são inicialmente funções gaussianas centradas no espaço.
Podemos observar que a onda diminui sua amplitude a medida que ela se propaga no espaço. Posteriormente, são observados fenômenos de interferência construtiva e destrutiva devido a reflexão da onda com as paredes da caixa.
Exemplo 2. Onda confinada em uma caixa com profundidade variável: utilizando a função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s = tanh(x)} foi possível simular uma onda chegando em uma praia, esse exemplo foi feito em 1D conservativo.
Para fazer esse exemplo usamos o código 1, porém desconsideramos as derivadas em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} e inicializamos os vetores da altura e velocidade com a discretização em apenas uma dimensão (abaixo descrevemos está parte do código). Deve-se notar que o problema passa a ter um índice, pois a discretização não forma mais uma malha, então pode ser retirado um laço for do código.
#%% Discretização do espaço x
x = np.linspace(L_x0, L_xf, NX)
#%% Condições iniciais da superficie e da agua
# Superficie
b = 5 * np.tanh((x- L_xf*0.3) / 2) # funcao tangente
b += np.full(shape=(np.shape(b)), fill_value=-np.min(b)) # aqui é somado só para a funcao comecar em zero
# Onda e velocidade
sigma = 1.0 # distribuicao da onda
sigma_v = 1.0 # distribuicao da onda
h_2d = 1.1 * max(b) * np.ones(shape=np.shape(x)) + np.exp(-((x)**2/(2*(sigma**2))))
h_2d -= b
u_2d = 0.08 * np.exp(-((x)**2/(2*(sigma_v**2))))
Forma dissipativa 2D
Os exemplos que seguem utilizam o código abaixo para calcular as equações de águas rasas não conservativa (38),(43) e (44) nos passos de tempo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta } , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle M } , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } , onde as funções em python atualiza_eta, atualiza_M, e atualiza_N implementam computacionalmente isto. Para implementar estas funções e outras ideias do nosso programa, o seguinte código fonte da referência [11] foi usado como base.
Códigos das Equações Não Conservativas
O código 4 foi escrito na linguagem Python e resolve o exemplo 3 que será apresentado abaixo.
Código 4 - Forma Não Conservativa das Equações de Águas Rasas
O código 5 foi escrito na linguagem Python e resolve o exemplo 4 que será apresentado abaixo.
Código 5 - Forma Não Conservativa das Equações de Águas Rasas
Exemplo 3 - Onda Confinada em uma Caixa
Através do código 4 fizemos a simulação da propagação de uma onda em uma caixa de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_x =100 } m e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_y = 100 } m em uma profundidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle h(x,y)=50} m. O fluxo de descarga e o deslocamento do volume de água inicial, ambas com suas devidas unidades físicas, são Gaussianas centradas em 80, com amplitude igual a 1 e largura igual a 70.
Exemplo 3 com coeficiente de Manning igual a 0.025.
Exemplo 3 com coeficiente de Manning igual a 20.0.
Dos gráficos acima, podemos observar que quanto maior for o coeficiente de Manning mais rápida a onda irá atenuar a sua amplitude. Está observação faz sentido, já que as forças de fricção sobre o fluído são maiores na situação em que o coeficiente de Manning tem maior valor.
Exemplo 4 - Tsunami
Simulação da propagação de uma onda em uma caixa de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_x =500} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_y =500 } Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m } , em uma profundidade variável, que respeita a função tangente hiperbólica. O fluxo de descarga e o deslocamento do volume de água inicial, ambas com suas devidas unidades físicas, são Gaussianas centradas em 300, com amplitude igual a 2 e largura igual a 500.
A medida que o fundo do oceano diminui sua profundidade a velocidade da onda diminui e a amplitude aumenta. Está simulação mostra o comportamento físico da propagação de um Tsunami em direção ao litoral.
Comparação entre Métodos
Onda confinada em uma caixa
Abaixo é mostrado o gráfico de evolução temporal da altura da onda em três pontos distintos do sistema (utilizando os mesmos parâmetros que foi aplicado ao método conservativo com a onda em uma caixa de profundidade constante em todos os outros métodos). Pode-se perceber que com o passar do tempo o movimento das duas equações começa a divergir, mesmo com o fator de fricção baixo.
Para o método 1D é de se esperar que exista menos interferências entre as ondas, pois só existe parede nos finais do sistema, além disso, a onda só precisa se espalhar em uma direção, então a sua amplitude é maior.
Também é possível perceber a diferença entre métodos observando apenas em uma direção (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{x}} ), por causa dos termos de fricção e viscosidade.
Referências
- ↑ Equação da continuidade mássica: balanços de massa diferenciais. Bloom Consultoria.Disponível em: <https://www.youtube.com/watch?v=pEip-GvO0LM&list=PL1yqHjPQz-Lqjri07DqZ3RsSWJfICvdiu&index=3>
- ↑ Equação de Navier-Stokes (Parte 1) - Derivadas materiais. Bloom Consultoria.Disponível em: https://www.youtube.com/watch?v=FLoZODPpayM
- ↑ Equação de Navier-Stokes (Parte 2) - Equação diferencial da quantidade de movimento. Bloom Consultoria.Disponível em: https://www.youtube.com/watch?v=e06ZRzdO4iM
- ↑ Equação de Navier-Stokes (Parte 3) - Tensões Normais e Cisalhantes. Bloom Consultoria.Disponível em: https://www.youtube.com/watch?v=na2kGOSYNv8
- ↑ SEGUR, Harvey; YAMAMOTO, Hiroki. Lecture 8: The Shallow-Water Equations.Disponível em: <https://docplayer.net/49487265-Lecture-8-the-shallow-water-equations.html>
- ↑ Leibniz integral rule. Disponível em: https://en.wikipedia.org/wiki/Leibniz_integral_rule
- ↑ 7,0 7,1 IMAMURA, Fumihiko.Tsunami Modelling Manual.Disponível em: http://www.tsunami.civil.tohoku.ac.jp/hokusai3/J/projects/manual-ver-3.1.pdf
- ↑ LINSLEY, Ray K.; FRANZINI, Joseph B. Water Resources Engineering.
- ↑ GARCÍA-NAVARRO, P; et al. The shallow water equations: An example of hyperbolic system. Espanha: 2008. Disponível em: <https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.571.1364&rep=rep1&type=pdf>
- ↑ KUHBACHER, Christian. Shallow Water: Derivation and Applications. Disponível em: <http://www.mathematik.tu-dortmund.de/lsiii/cms/papers/Kuehbacher2009.pdf>
- ↑ KOEHN, Daniel. 2D Shallow Water Equations. Disponível em: <https://github.com/daniel-koehn/Differential-equations-earth-system/blob/master/10_Shallow_Water_Equation_2D/01_2D_Shallow_Water_Equations.ipynb>