Equação de Burgers: mudanças entre as edições
Sem resumo de edição |
|||
| (31 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
<span style="color:#ff0000"> (EM EDIÇÃO)</span> | <!--<span style="color:#ff0000"> (EM EDIÇÃO)</span>--> | ||
'''Grupo: Eduardo Pedroso, Luis Gustavo Lang Gaiato e William Machado Pantaleão''' | |||
'''Grupo: Eduardo Pedroso, Luis Gustavo Lang Gaiato | |||
Um dos maiores desafios no campo dos [https://en.wikipedia.org/wiki/Complex_system sistemas complexos] é a compreensão do fenômeno de turbulência. Simulações computacionais contribuíram bastante para o entendimento dessa área, no entanto, ainda não existe nenhuma teoria que explique com sucesso esse comportamento e permita prever outros importantes fenômenos como misturas, convecção e combustão turbulentas, com base nas equações fundamentais da dinâmica de fluidos. Isso se deve ao fato de que a equação para os fluidos mais simples (incompressíveis) já deve levar em consideração propriedades não lineares <ref name=White> F. M. White, Viscous Fluid Flow, 3rd ed. New York, NY: McGraw-Hill Professional, 2005. | Um dos maiores desafios no campo dos [https://en.wikipedia.org/wiki/Complex_system sistemas complexos] é a compreensão do fenômeno de turbulência. Simulações computacionais contribuíram bastante para o entendimento dessa área, no entanto, ainda não existe nenhuma teoria que explique com sucesso esse comportamento e permita prever outros importantes fenômenos como misturas, convecção e combustão turbulentas, com base nas equações fundamentais da dinâmica de fluidos. Isso se deve ao fato de que a equação para os fluidos mais simples (incompressíveis) já deve levar em consideração propriedades não lineares <ref name=White> F. M. White, Viscous Fluid Flow, 3rd ed. New York, NY: McGraw-Hill Professional, 2005. | ||
| Linha 123: | Linha 122: | ||
== Modelo de Deposição - Crescimento de Interfaces == | == Modelo de Deposição - Crescimento de Interfaces == | ||
[[Arquivo:kpzgrow.gif|275px|thumb|right|'''Figura 1''': Modelo de deposição balística (pertencente à família dos modelos KPZ). O modelo é como um tetris onde os blocos caem e se fixam no primeiro contato <ref name='Halpin'> Halpin-Healy, T., 2015. KPZ growth model - ballistic deposition (BD). [online] Youtube.com. Disponível em: <https://youtu.be/pdeswgu9rS8> [Acessado em 30 Setembro de 2021] </ref>.]] | [[Arquivo:kpzgrow.gif|275px|thumb|right|'''Figura 1''': Modelo de deposição balística (pertencente à família dos modelos KPZ). O modelo é como um tetris onde os blocos caem e se fixam no primeiro contato <ref name='Halpin'> Halpin-Healy, T., 2015. KPZ growth model - ballistic deposition (BD). [online] Youtube.com. Disponível em: <https://youtu.be/pdeswgu9rS8> [Acessado em 30 Setembro de 2021] </ref>.]] | ||
Um exemplo de aplicação é no crescimento de interfaces por deposição, já que a equação de Burgers é equivalente a equação conhecida como, [https://en.wikipedia.org/wiki/Kardar%E2%80%93Parisi%E2%80%93Zhang_equation ''equação de Kardar-Parisi-Zhang''] (equação ''KPZ''), um modelo de crescimento de uma superfície sólida por deposição de vapor (ou erosão de material de uma superfície sólida), que mostra a evolução da altura da camada com o tempo <ref name=Reis> | Um exemplo de aplicação é no crescimento de interfaces por deposição, já que a equação de Burgers é equivalente a equação conhecida como, [https://en.wikipedia.org/wiki/Kardar%E2%80%93Parisi%E2%80%93Zhang_equation ''equação de Kardar-Parisi-Zhang''] (equação ''KPZ''), um modelo de crescimento de uma superfície sólida por deposição de vapor (ou erosão de material de uma superfície sólida), que mostra a evolução da altura da camada com o tempo <ref name=Reis>Reis, F. D. A. A. Depinning transitions in interface growth models. Brazilian journal of physics, v. 33, n. 3, p. 501–513, 2003</ref>. | ||
<math>\frac{\partial}{\partial t} h(x, t)-\frac{1}{2}\left(\nabla h(x, t)\right)^{2}=\nu \frac{\partial^{2}}{\partial x^{2}} h(x, t)+F(x, t)</math> | <math>\frac{\partial}{\partial t} h(x, t)-\frac{1}{2}\left(\nabla h(x, t)\right)^{2}=\nu \frac{\partial^{2}}{\partial x^{2}} h(x, t)+F(x, t)</math> | ||
| Linha 133: | Linha 132: | ||
A velocidade é assumida como sendo proporcional ao gradiente de <math>h(x,t)</math> (superfície evolui na direção do gradiente). A difusão da superfície é descrita pelo termo de difusão. | A velocidade é assumida como sendo proporcional ao gradiente de <math>h(x,t)</math> (superfície evolui na direção do gradiente). A difusão da superfície é descrita pelo termo de difusão. | ||
A equação KPZ | A equação KPZ unidimensional corresponde a versão estocástica da equação de Burgers com campo <math>u(x,t)</math> pela substituição <math>u=-\lambda\frac{\partial h}{\partial x}</math>. | ||
== Solução de Onda Viajante == | == Solução de Onda Viajante == | ||
| Linha 213: | Linha 212: | ||
Portanto: | Portanto: | ||
<math> u(x, t)=\frac{u_{D}+u_{E}}{2}-\frac{u_{E}-u_{D}}{2} \tanh \left(\frac{\left(\ | <math> u(x, t)=\frac{u_{D}+u_{E}}{2}-\frac{u_{E}-u_{D}}{2} \tanh \left(\frac{\left(\Delta x-s t\right)\left(u_{E}-u_{D}\right)}{4 \nu}\right) </math> | ||
=== Gráfico === | === Gráfico === | ||
| Linha 269: | Linha 268: | ||
anim = FuncAnimation(fig, animate, init_func=init, # funcao que produz a animacao | anim = FuncAnimation(fig, animate, init_func=init, # funcao que produz a animacao | ||
frames=50, interval=100, blit=True) # 50 frames com intervalo de 0.1s | frames=50, interval=100, blit=True) # 50 frames com intervalo de 0.1s | ||
anim.save('shockwaveee.gif', writer='imagemagick') # gera um .GIF (e | anim.save('shockwaveee.gif', writer='imagemagick') # gera um .GIF (e renderizacao) | ||
</source> | </source> | ||
== Velocidade de Choque == | == Velocidade de Choque == | ||
Tomando a viscosidade como nula, a equação de Burgers pode ser reescrita como<ref name=Cameron>Cameron, M. Notes on Burgers's Equation. University of Maryland, 2021</ref>: | |||
<math> \frac{\partial u(x,t)}{\partial t} + \frac{\partial}{\partial x}\frac{u^{2}}{2} = 0 </math> | |||
Cuja solução é dada na forma e uma onda viajante: | |||
<math> u(x,t)=V(\Delta x - st) </math> | |||
Onde <math>V(y)</math> é uma função degrau: | |||
<math> \left\{\begin{array}{l} | |||
u_{E}\text{ para } y<0\\ | |||
u_{D}\text{ para } y>0 | |||
\end{array}\right. </math> | |||
Onde <math>u_{E}>u_{D}</math>. Essa onda é chamada de [https://en.wikipedia.org/wiki/Shock_wave onda de choque], e possui velocidade de propagação <math>s</math>. Por conservação, [https://en.wikipedia.org/wiki/Rankine%E2%80%93Hugoniot_conditions#The_jump_condition a condição de salto]: | |||
<math> \frac{d}{d t} \int_{-M}^{M} u(x, t) d x=\int_{-M}^{M}-u u_{x} d x=-\left.\frac{u^{2}}{2}\right|_{-M} ^{M}=\frac{u_{E}^{2}}{2}-\frac{u_{D}^{2}}{2} </math> | |||
== | Por outro lado: | ||
<math> \int_{-M}^{M} u(x, t) d x=(M+s t) u_{E}+(M-s t) u_{D} </math> | |||
Portanto: | |||
<math> \frac{d}{d t} \int_{-M}^{M} u(x, t) d x=s\left(u_{E}-u_{D}\right) </math> | |||
Dessa forma: | |||
<math> s=\left(\frac{u_{E}^{2}}{2}-\frac{u_{D}^{2}}{2}\right) /\left(u_{E}-u_{D}\right)=\frac{u_{E}+u_{D}}{2} </math> | |||
O caso generalizado da velocidade de propagação de uma onda de choque é conhecido como [https://en.wikipedia.org/wiki/Rankine%E2%80%93Hugoniot_conditions condição de Rankine-Hugoniot], e pode ser obtido, desse resultado, pela aplicação das leis de conservação hiperbólicas: | |||
<math> \frac{\partial u}{\partial t}+\frac{\partial}{\partial x} f(u)=0 </math> | |||
Assim: | |||
<math> s=\frac{f\left(u_{E}\right)-f\left(u_{D}\right)}{u_{E}-u_{D}} = \frac{\text{salto em }f(u)}{\text{salto em }u} </math> | |||
A condição de Rankine-Hugoniot, onde o salto da função é definido como choque. | |||
== Métodos Numéricos == | == Métodos Numéricos == | ||
Discretizando a equação de Burgers para um fluido víscido, a partir da abordagem FTCS ([https://en.wikipedia.org/wiki/FTCS_scheme ''Foward Time Central Space'']), com a derivada à direita: | |||
<math> \cfrac{\partial}{\partial{t}}u(x,t) = \cfrac{u(x,t+\Delta t) - u(x,t)}{\Delta t} +\mathcal{O}(\Delta t^{2}) </math> | |||
<math> \cfrac{\partial^{2}}{\partial{x^{2}}}u(x,t) = \cfrac{u(x+\Delta x, t) - 2u(x,t) + u(x-\Delta x,t)}{(\Delta t)^{2}} +\mathcal{O}(\Delta x^{3}) </math> | |||
Se: | |||
<math> \left\{\begin{array}{l} | |||
u(x, t) := U_{i}^{n}\\ | |||
u(x, t+\Delta t) := U_{i}^{n+1}\\ | |||
u(x+\Delta x, t) := U_{i+1}^{n} | |||
\end{array}\right. </math> | |||
<math> \implies \cfrac{\partial{u}}{\partial{t}}+u\cfrac{\partial{u}}{\partial{x}}=\nu\cfrac{\partial^{2}{U}}{\partial{x^{2}}} \longrightarrow \cfrac{U_{i}^{n+1}-U_{i}^{n}}{\Delta t} + U_{i}^{n}\cfrac{U_{i}^{n}-U_{i-1}^{n}}{\Delta x} = \nu\cfrac{U_{i+1}^{n}-2U_{i}^{n}+U_{i-1}^{n}}{(\Delta x)^{2}} </math> | |||
<math> \longrightarrow U_{i}^{n+1} = U_{i}^{n} - U_{i}^{n}\cfrac{\Delta t}{\Delta x}(U_{i}^{n}-U_{i-1}^{n})+\nu\cfrac{\Delta t}{(\Delta x)^{2}}(U_{i+1}^{n}-2U_{i}^{n}+U_{i-1}^{n}) </math> | |||
=== Conservação === | === Conservação === | ||
Um dos problemas no cálculo de soluções descontinuas para equações como a de Burgers pode ser exemplificado da seguinte forma; supondo a equação de Burgers na forma ''quasi''-linear com viscosidade nula:<ref name=Cameron></ref> | |||
<math> \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} = 0 </math> | |||
Com condições iniciais: | |||
<math> u(x, 0)=u_{0}(x)= \begin{cases}1, & x<0 \\ 0, & x \geq 0\end{cases} </math> | |||
Pela discretização feita anteriormente: | |||
<math> U_{i}^{n+1} = U_{i}^{n} - U_{i}^{n}\cfrac{\Delta t}{\Delta x}(U_{i}^{n}-U_{i-1}^{n})+\nu\cfrac{\Delta t}{(\Delta x)^{2}}(U_{i+1}^{n}-2U_{i}^{n}+U_{i-1}^{n}) </math> | |||
Pelas condições iniciais, <math>U_{i}^{0}=1</math> para <math>i<0</math> e <math>U_{i}^{0}=0</math> para <math>i\geq 0</math>: | |||
<math> U_{i}^{1}= \begin{cases}1-\frac{\Delta t}{\Delta x} 1(1-1)=1, & i<0 \\ 0-\frac{\Delta t}{\Delta x} 0\left(0-U_{i-1}^{0}\right)=0, & i \geq 0\end{cases} </math> | |||
Como resultado, <math>U_{i}^{1}=U_{i}^{0}</math>. Dessa forma, <math>U_{i}^{n}=U_{i}^{0}</math>; isso significa que o método propaga a descontinuidade (onda de choque) com a velocidade incorreta, <math>s=0</math>; ou seja, não ocorre propagação após o choque. | |||
==== Método Conservativo ==== | |||
A partir da discretização para o caso víscido, se <math>\nu=0</math>, então: | |||
<math>U_{i}^{n+1} = U_{i}^{n} - U_{i}^{n}\cfrac{\Delta t}{\Delta x}(U_{i}^{n}-U_{i-1}^{n})</math> | |||
Assim como para o caso anterior, esse método não é conservativo e é adequado apenas para soluções que não possuem descontinuidades. Considerando a [https://en.wikipedia.org/wiki/Conservation_law lei de conservação]: | |||
<math>\frac{\partial u}{\partial t} + \frac{\partial}{\partial x}f(u) = 0</math> | |||
Discretizando: | |||
<math>U_{i}^{n+1}=U_{i}^{n}-\frac{\Delta t}{\Delta x}\left[f\left(U_{i}^{n}\right)-f\left(U_{i-1}^{n}\right)\right]</math> | |||
Onde a função <math>f</math> corresponde à uma função de <math>p+q+1</math> argumentos, chamada de fluxo numérico <ref name=Cameron></ref> <ref name=Mikel>Landajuela, M. Burgers Equation. Basque Center for Applied Mathematics, 2011</ref> <ref name=LeVeque>LeVeque, Randall J. (1992). Numerical Methods for Conservation Laws (PDF). Boston: Birkhäuser. p. 125. ISBN 0-8176-2723-5.</ref>. Assim, para <math>p=1</math> e <math>q=0</math>, <math>F(U,V)=f(u)</math>: | |||
<math>U_{i}^{n+1}=U_{i}^{n}-\frac{\Delta t}{\Delta x}\left[\frac{1}{2}\left(U_{i}^{n}\right)^{2}-\frac{1}{2}\left(U_{i-1}^{n}\right)^{2}\right]</math> | |||
=== Lax-Friedrichs === | === Lax-Friedrichs === | ||
O método de [https://en.wikipedia.org/wiki/Lax%E2%80%93Friedrichs_method Lax-Friedrichs] para sistemas não lineares possui a forma: | |||
<math>U_{i}^{n+1}=\frac{1}{2}\left(U_{i-1}^{n}+U_{i+1}^{n}\right)-\frac{k}{2 h}\left[f\left(U_{i+1}^{n}\right)-f\left(U_{i-1}^{n}\right)\right]</math> | |||
Para o caso da equação de Burgers invíscida: | |||
<math>U_{i}^{n+1}=\frac{1}{2}\left(U_{i-1}^{n}+U_{i+1}^{n}\right)-\frac{\Delta t}{2 \Delta x}\left[\frac{1}{2}\left(U_{i+1}^{n}\right)^{2}-\frac{1}{2}\left(U_{i-1}^{n}\right)^{2}\right]</math> | |||
=== Lax-Wendroff === | === Lax-Wendroff === | ||
O método de [https://en.wikipedia.org/wiki/Lax%E2%80%93Friedrichs_method Lax-Wendroff] é um método de segunda ordem e possui a forma <ref name=LeVeque></ref><ref name=Mikel></ref>: | |||
<math>U_{i}^{n+1}=U_{i+1}^{n}-\frac{k}{2 h}\left(f\left(U_{i+1}^{n}\right)-f\left(U_{i-1}^{n}\right)\right)+\frac{k^{2}}{2 h^{2}}\left[A_{i+\frac{1}{2}}\left(f\left(U_{i+1}^{n}\right)-f\left(U_{i}^{n}\right)\right)-A_{i-\frac{1}{2}}\left(f\left(U_{i}^{n}\right)-f\left(U_{i-1}^{n}\right)\right)\right]</math> | |||
Onde <math>A_{j\pm\frac{1}{2}}</math> corresponde à matriz jacobiana <math>A(u)=f^{\prime}(u)</math>, avaliada em <math>1/2(U_{i}^{n}+U_{j\pm1}^{n})</math>. Para a equação de Burgers (invíscida) <math>f^{\prime}(u)=u</math>, assim: | |||
<math>U_{i}^{n+1}= U_{i+1}^{n}-\frac{k}{2 h}\left(\frac{1}{2}\left(U_{i+1}^{n}\right)^{2}-\frac{1}{2}\left(U_{i-1}^{n}\right)^{2}\right)+</math> | |||
<math>\frac{k^{2}}{2 h^{2}}\left[\left(\frac{1}{2}\left(U_{i}^{n}+U_{i+1}^{n}\right)\right)\left(\frac{1}{2}\left(U_{i+1}^{n}\right)^{2}-\frac{1}{2}\left(U_{i}^{n}\right)^{2}\right)-\left(\frac{1}{2}\left(U_{i}^{n}+U_{i-1}^{n}\right)\right)\left(\frac{1}{2}\left(U_{i}^{n}\right)^{2}-\frac{1}{2}\left(U_{i-1}^{n}\right)^{2}\right)\right]</math> | |||
=== Método parabólico === | |||
Considerando a equação de Burgers víscida com <math>f(u)=u^{2}/2</math>, na forma <ref name=Mikel></ref>: | |||
<math>\frac{\partial u}{\partial t} + \frac{\partial}{\partial x}f(u) = \nu\frac{\partial^{2} u}{\partial x^{2}}</math> | |||
Integrando de <math>x_{i-1/2}</math> até <math>x_{i+1/2}</math>: | |||
<math>\int_{x_{i-1 / 2}}^{x_{i+1 / 2}} \frac{\partial u}{\partial t} d x-\left[\nu\frac{\partial u}{\partial x}\right]_{x_{i-1 / 2}}^{x_{i+1 / 2}}=-[f(u)]_{x_{i-1 / 2}}^{x_{i+1 / 2}}</math> | |||
Aproximando-se cada termo da equação acima tem-se que, para o primeiro termo: | |||
<math>\int_{x_{i-1 / 2}}^{x_{i+1 / 2}} \frac{\partial u}{\partial t} d x \approx \frac{d u}{d t}\left(x_{i}, t\right) h</math> | |||
Para o segundo: | |||
<math>-\left[\nu\frac{\partial u}{\partial x}\right]_{x_{i-1 / 2}}^{x_{i+1 / 2}}=\nu\left[\frac{\partial u}{\partial x}\left(x_{i-1 / 2}, t\right)-\frac{\partial u}{\partial x}\left(x_{i+1 / 2}, t\right)\right]</math> | |||
<math>\implies -\left[\nu\frac{\partial u}{\partial x}\right]_{x_{i-1 / 2}}^{x_{i+1 / 2}} \approx \nu\left[\frac{u\left(x_{i}, t\right)-u\left(x_{i-1}, t\right)}{h}-\frac{u\left(x_{i+1}, t\right)-u\left(x_{i}, t\right)}{h}\right] = -\nu \frac{u\left(x_{i+1}, t\right)-2 u\left(x_{i}, t\right)+u\left(x_{i-1}, t\right)}{h}</math> | |||
Para o terceiro: | |||
<math>-[f(u)]_{x_{i-1 / 2}}^{x_{i+1 / 2}}=f\left(u\left(x_{i-1 / 2}, t\right)\right)-f\left(u\left(x_{i+1 / 2}, t\right)\right)</math> | |||
Substituindo as aproximações na expressão completa e definindo <math>U_{i}(t)\equiv u(x_{i},t)</math>: | |||
<math>\frac{d U_{i}}{d t}-\nu \frac{U_{i+1}-2 U_{i}+U_{i-1}}{h^{2}}=\frac{f\left(U_{i-\frac{1}{2}}\right)-f\left(U_{i+\frac{1}{2}}\right)}{h}</math> | |||
Discretizando a derivada em relação a tempo por um método FTCS: | |||
<math>U_{i}^{n+1}=U_{i}^{n}+k\left(\nu \frac{U_{i+1}^{n}-2 U_{i}^{n}+U_{i-1}^{n}}{h^{2}}-\frac{f\left(U_{i+\frac{1}{2}}^{n}\right)-f\left(U_{i-\frac{1}{2}}\right)}{h}\right)</math> | |||
Onde <math>f(U_{i\pm\frac{1}{2}})</math> é calculada numericamente como a média entre <math>f(U_{i})</math> e <math>f(U_{i\pm 1})</math>. | |||
== Implementação == | == Implementação == | ||
Foram implementados quatro métodos: para o caso víscido, FTCS não conservativo e o método parabólico; para o caso invíscido, FTCS não conservativo e FTCS conservativo. Definindo a condição de contorno periódica <math>U_{i=0}^{n}=u_{i_{max}}^{n}</math>, e utilizando as condições iniciais: | |||
Caso 1: | |||
<math>u(x, t)= \begin{cases}1, & x \leq 1 \\ 0, & x>1\end{cases}</math> | |||
Caso 2: | |||
<math>\left\{\begin{array}{l} | |||
u_{i}^{n=0}=\frac{-2 \nu}{\phi(x, \nu)}\left(\frac{\partial \phi(x, \nu)}{\partial x}\right)+4 \\ | |||
\phi=e^{\left(\frac{-x^{2}}{4 \nu}\right)+e^{\left[\frac{-(x-2 \pi)^{2}}{4 \nu}\right]}} | |||
\end{array}\right.</math> | |||
Derivando <math>\phi</math> e substituindo na equação: | |||
<math>\implies u_{i}^{n=0} = -\cfrac{x}{2\nu}e^{\left(\cfrac{-x^{2}}{4\nu}\right)}-\cfrac{(x-2\pi)}{2\nu}e^{\left[\cfrac{-(x-2\pi)^{2}}{4\nu}\right]}</math> | |||
Cuja solução analítica é | |||
<math>\left\{\begin{array}{l} | |||
u_{i}^{n}=\frac{-2 \nu}{\phi(x, \nu)}\left(\frac{\partial \phi(x, \nu)}{\partial x}\right)+4 \\ | |||
\phi=e^{\left(\frac{-(x-4 t)^{2}}{4 \nu(t+1)}\right)+e^{\left[\frac{-(x-4 t-2 \pi)^{2}}{4 \nu(t+1)}\right]}} | |||
\end{array}\right.</math> | |||
Derivando <math>\phi</math> e substituindo na equação: | |||
<math>u_{i}^{n}=-\frac{(x-4 t)}{2 \nu(t+1)} e^{-\left(\frac{(x-4 t)^{2}}{4 \nu(t+1)}\right)}-\frac{(x-4 t-2 \pi)}{2 \nu(t+1)} e^{\left[\frac{-(x-4 t-2 \pi)^{2}}{4 \nu(t+1)}\right]}</math> | |||
=== Importando os Módulos Utilizados === | |||
<source lang="python"> | |||
# -*- coding: utf-8 -*- | |||
from math import pi, exp | |||
import numpy as np | |||
import matplotlib.pyplot as plt | |||
import matplotlib.cm as cm | |||
Array2D = np.ndarray # typing... | |||
</source> | |||
=== Burgers FTCS Víscido Não Conservativo === | |||
<source lang="python"> | |||
def burgers(nt:int, nx:int, tmax:float, xmax:float, v:float, caso:int) -> tuple: | |||
# incrementos | |||
dt = tmax/(nt-1) # no tempo | |||
dx = xmax/(nx-1) # no espaco | |||
# arrays | |||
u = np.zeros((nx, nt)) # velocidade | |||
x = np.zeros(nx) | |||
ipos = np.zeros(nx) | |||
ineg = np.zeros(nx) | |||
# condicoes de contorno periodicas | |||
for i in range(0, nx): # i: 0, 1, ... nx-2, nx-1, nx | |||
x[i] = i*dx | |||
ipos[i] = i+1 # 1, 2, ... nx-2, nx+1 | |||
ineg[i] = i-1 # -1, 0, ... nx-2, nx-1 | |||
ipos[-1] = 0 # ipos[nx-1] = 0, u_{n+1} | |||
ineg[0] = nx-1 # u_{n-1} | |||
# condicoes iniciais | |||
if caso == 1: | |||
for i in range(0,nx): | |||
if x[i] <= 1: | |||
u[i,0] = 1 | |||
elif x[i] > 1: | |||
u[i,0] = 0 | |||
elif caso == 2: | |||
for i in range(0, nx): | |||
phi = exp( -(x[i]**2)/(4*v) ) + exp( -(x[i]-2*pi)**2 / (4*v) ) | |||
dphi = (-(0.5*x[i]/v)*exp( -(x[i]**2) / (4*v) ) - (0.5*(x[i]-2*pi) / v ) | |||
*exp(-(x[i]-2*pi)**2 / (4*v) )) | |||
u[i,0] = -2*v*(dphi/phi) + 4 | |||
# solucao numerica | |||
for n in range(0, nt-1): | |||
for i in range(0,nx): | |||
u[i,n+1] = (u[i,n]-u[i,n]*(dt/dx)*(u[i,n]-u[int(ineg[i]),n])+ | |||
v*(dt/dx**2)*(u[int(ipos[i]),n]-2*u[i,n]+u[int(ineg[i]),n])) | |||
return((u, x)) | |||
</source> | |||
=== Burgers Víscido Parabólico === | |||
<source lang="python"> | |||
def burgParab(nt:int, nx:int, tmax:float, xmax:float, v:float, caso:int) -> tuple: | |||
def f(u): | |||
return((u**2)/2) | |||
# incrementos | |||
dt = tmax/(nt-1) | |||
dx = xmax/(nx-1) | |||
# arrays | |||
u = np.zeros((nx,nt)) | |||
x = np.zeros(nx) | |||
ipos = np.zeros(nx) | |||
ineg = np.zeros(nx) | |||
# condicoes de contorno periodicas | |||
for i in range(0,nx): | |||
x[i] = i*dx | |||
ipos[i] = i+1 | |||
ineg[i] = i-1 | |||
ipos[nx-1] = 0 | |||
ineg[0] = nx-1 | |||
# condicoes iniciais | |||
if caso == 1: | |||
for i in range(0,nx): | |||
if x[i] <= 1: | |||
u[i,0] = 1 | |||
elif x[i] > 1: | |||
u[i,0] = 0 | |||
elif caso == 2: | |||
for i in range(0,nx): | |||
phi = exp( -(x[i]**2)/(4*v) ) + exp( -(x[i]-2*pi)**2 / (4*v) ) | |||
dphi = (-(0.5*x[i]/v)*exp( -(x[i]**2) / (4*v) ) - (0.5*(x[i]-2*pi) / v ) | |||
*exp(-(x[i]-2*pi)**2 / (4*v) )) | |||
u[i,0] = -2*v*(dphi/phi) + 4 | |||
# solucao numerica | |||
for n in range(0,nt-1): | |||
for i in range(0,nx): | |||
fminus = 0.5*(f(u[i,n]) + f(u[int(ineg[i]),n])) | |||
fplus = 0.5*(f(u[i,n]) + f(u[int(ipos[i]),n])) | |||
u[i,n+1] = u[i,n]+dt*(v*((u[int(ipos[i]),n]-(2*u[i,n])+u[int(ineg[i]),n])/(dx**2))-(fplus-fminus)/dx) | |||
return((u, x)) | |||
</source> | |||
=== Burgers Víscido Analítico (Caso 2) === | |||
<source lang="python"> | |||
def burgers_analytical(nt:int, nx:int, tmax:float, xmax:float, v:float) -> tuple: | |||
# incrementos | |||
dt = tmax/(nt-1) | |||
dx = xmax/(nx-1) | |||
# arrays | |||
u_a = np.zeros((nx, nt)) | |||
x = np.zeros(nx) | |||
t = np.zeros(nt) | |||
# len(x) | |||
for i in range(0, nx): | |||
x[i] = i*dx | |||
# solucao analitica | |||
for n in range(0, nt): | |||
t = n*dt | |||
for i in range(0, nx): | |||
phi = (exp( -(x[i]-4*t)**2/(4*v*(t+1)) ) + | |||
exp( -(x[i]-4*t-2*pi)**2/(4*v*(t+1)) )) | |||
dphi = ( -0.5*(x[i]-4*t)/(v*(t+1))*exp( -(x[i]-4*t)**2/(4*v*(t+1)) ) | |||
-0.5*(x[i]-4*t-2*pi)/(v*(t+1))*exp( -(x[i]-4*t-2*pi)**2/(4*v*(t+1)) ) ) | |||
u_a[i,n] = -2*v*(dphi/phi) + 4 | |||
return((u_a, x)) | |||
</source> | |||
=== Burgers FTCS Invíscido Não Conservativo === | |||
<source lang="python"> | |||
== | def burgInv(nt:int, nx:int, tmax:float, xmax:float) -> tuple: | ||
# incrementos | |||
dt = tmax/(nt-1) | |||
dx = xmax/(nx-1) | |||
# arrays | |||
u = np.zeros((nx,nt)) | |||
x = np.zeros(nx) | |||
ipos = np.zeros(nx) | |||
ineg = np.zeros(nx) | |||
# condicoes de contorno periodicas | |||
for i in range(0,nx): | |||
x[i] = i*dx | |||
ipos[i] = i+1 | |||
ineg[i] = i-1 | |||
ipos[nx-1] = 0 | |||
ineg[0] = nx-1 | |||
# condicoes iniciais | |||
for i in range(0,nx): | |||
if x[i]<=1: | |||
u[i,0] = 1 | |||
elif x[i]>1: | |||
u[i,0] = 0 | |||
# solucao numerica | |||
for n in range(0,nt-1): | |||
for i in range(0,nx): | |||
u[i,n+1] = (u[i,n]-u[i,n]*(dt/dx)*(u[i,n]-u[int(ineg[i]),n])) | |||
return((u, x)) | |||
</source> | |||
=== Burgers FTCS Invíscido Conservativo === | |||
<source lang="python"> | |||
def burgCons(nt:int, nx:int, tmax:float, xmax:float) -> tuple: | |||
# incrementos | |||
dt = tmax/(nt-1) | |||
dx = xmax/(nx-1) | |||
# arrays | |||
u = np.zeros((nx,nt)) | |||
x = np.zeros(nx) | |||
ipos = np.zeros(nx) | |||
ineg = np.zeros(nx) | |||
# condicoes de contorno periodicas | |||
for i in range(0,nx): | |||
x[i] = i*dx | |||
ipos[i] = i+1 | |||
ineg[i] = i-1 | |||
ipos[nx-1] = 0 | |||
ineg[0] = nx-1 | |||
# condicoes iniciais | |||
for i in range(0,nx): | |||
if x[i]<=1: | |||
u[i,0] = 1 | |||
elif x[i]>1: | |||
u[i,0] = 0 | |||
# solucao numerica | |||
for n in range(0,nt-1): | |||
for i in range(0,nx): | |||
u[i,n+1] = (u[i,n]-(dt/dx)*((1/2 * (u[i,n])**2)-(1/2 * (u[int(ineg[i]),n])**2))) | |||
return((u, x)) | |||
</source> | |||
=== Gráfico de <math>u</math> e <math>u_{a}</math> ''vs.'' <math>x</math> === | |||
<source lang="python"> | |||
def plot(u_a:Array2D, u:Array2D, x:list, nt:int, title:str): | |||
plt.figure(figsize=(8, 6), dpi=80) | |||
colour=iter(cm.rainbow(np.linspace(0, 20, nt))) | |||
for n in range(0, nt, 20): | |||
c=next(colour) | |||
plt.plot(x, u[:, n], 'ko', markerfacecolor=c, alpha=0.5) | |||
plt.plot(x, u_a[:, n], linestyle='-', c=c, label=f'i={n}') | |||
plt.legend() | |||
plt.xlabel(r'$x$') | |||
plt.ylabel(r'$u$') | |||
plt.ylim([0, 8.0]) | |||
plt.xlim([0, max(x)]) | |||
plt.title(title) | |||
plt.show() | |||
</source> | |||
=== Gráfico de <math>u</math>, <math>u_{p}</math> e <math>u_{a}</math> ''vs.'' <math>x</math> na Última Iteração === | |||
<source lang="python"> | |||
def plotErro(u:Array2D, u_p:Array2D, u_a:Array2D, x:list, v:float): | |||
plt.plot(x, u[:,-10], label='Burgers', color='blue') | |||
plt.plot(x, u_a[:,-10], label='Analítico', color='red') | |||
plt.plot(x, u_p[:,-10], label='Parabólico', color='green') | |||
plt.legend() | |||
plt.xlabel(r'$x$') | |||
plt.ylabel(r'$u$') | |||
plt.title('Última Interação com ' + r'$\nu=$' + f'{v}') | |||
plt.show() | |||
</source> | |||
=== Gráfico 3D Invíscido (Caso 1) === | |||
<source lang="python"> | |||
def plot3D(num:int, arr:Array2D, xmax:int, tmax:int, n:int, nx:int, title:str, cond:int) -> None: | |||
w_arr = np.zeros((num,len(arr[:,-1]))) | |||
x_arr = np.zeros((num,len(arr[:,-1]))) | |||
for i in range(num): | |||
if cond == 0: | |||
w, x_res = burgInv(nt, nx, n*i/num, xmax) | |||
elif cond == 1: | |||
w, x_res = burgCons(nt, nx, n*i/num, xmax) | |||
elif cond == 2: | |||
w, x_res = burgParab(nt, nx, n*i/num, xmax, 0.1,2) | |||
elif cond == 3: | |||
w, x_res = burgers(nt, nx, n*i/num, xmax, 0.1, 2) | |||
w_arr[i] = w[:,-1] | |||
x_arr[i] = x_res | |||
ax = plt.axes(projection='3d') | |||
times = np.zeros((num,1)) | |||
t = 0 | |||
dt = 0 | |||
for i in range(num): | |||
times[i,0] = t + dt | |||
dt += tmax/num | |||
ax.plot_surface(x_arr, times, w_arr, rstride=1, cstride=1, | |||
cmap='jet', edgecolor='none') | |||
plt.title(title) | |||
ax.set_xlabel('x') | |||
ax.set_ylabel('t') | |||
ax.set_zlabel('u') | |||
plt.show() | |||
</source> | |||
=== Exemplo de Utilização === | |||
Define-se <math>\nu=0.1</math>, <math>n_{t}=200</math>, <math>n_{x}=200</math>, <math>t_{max}=0.5</math> e <math>x_{max}=2\pi</math>: | |||
<source lang="python"> | |||
nt, nx, tmax, xmax, v = 200, 200, 0.5, 2*pi, 0.1 | |||
</source> | |||
Chama-se as funções de cálculo e constrói os gráficos: | |||
<source lang="python"> | |||
u, x = burgers(nt, nx, tmax, xmax, v, 2) # ftcs nao conservativo | |||
u_a, x = burgers_analytical(nt, nx, tmax, xmax, v) # ftcs analítico | |||
u_p, x = burgParab(nt, nx, tmax, xmax, v, 2) # # ftcs parabolico | |||
title = str(r'($\nu=$'+f'{v}, '+r'$n_t$'+f'={nt}, '+ | |||
r'$n_x$'+f'={nx}, '+r'$t_{max}$'+f'={tmax})') | |||
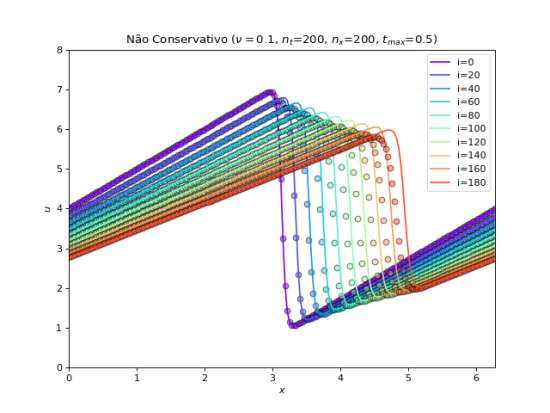
plot(u_a, u, x, nt, 'Não Conservativo ' + title) # grafico de u e u_a vs. x | |||
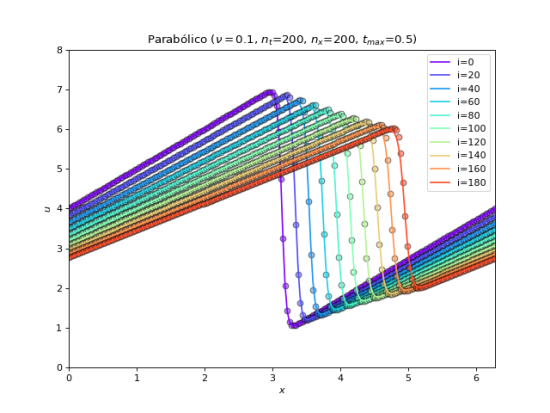
plot(u_a, u_p, x, nt, 'Parabólico ' + title) # grafico de u_p e u_a vs. x | |||
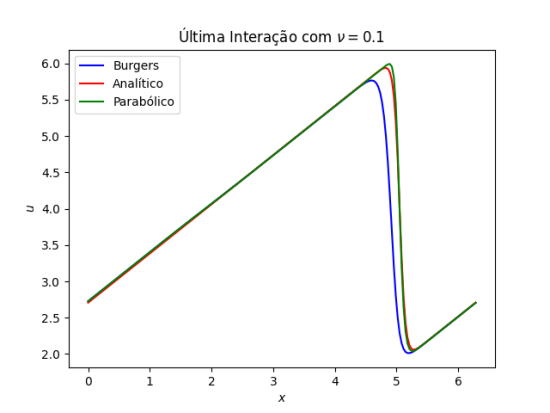
plotErro(u, u_p, u_a, x, v) | |||
</source> | |||
==== Como Resultado ==== | |||
<gallery class="center" mode=packed heights=275px> | |||
U_ncon.png|Gráfico da solução numérica e analítica para a equação de Burgers víscida utilizando FTCS não conservativo. | |||
U_parab.png|Gráfico da solução numérica e analítica para a equação de Burgers víscida utilizando o método parabólico. | |||
Burgers_erro.png|Comparação da última iteração de dois métodos numéricos, FTCS não conservativo (Burgers) e parabólico, para a equação de Burgers víscida, com sua solução analítica. | |||
</gallery> | |||
É possível observar que o método não conservativo propaga a descontinuidade com velocidade incorreta, ao contrário do método parabólico. De fato, como demonstrado anteriormente (ver [[#Conserva.C3.A7.C3.A3o|Conservação]]), no caso em que <math>\nu=0</math>, pelo método não conservativo a velocidade é nula. | |||
=== Para o Caso Invíscido === | |||
<source lang="python"> | |||
u_nc, x_nc = burgInv(nt, 100, 4, 2) | |||
title = 'Burgers Invíscido (não conservativo) - Caso 1' | |||
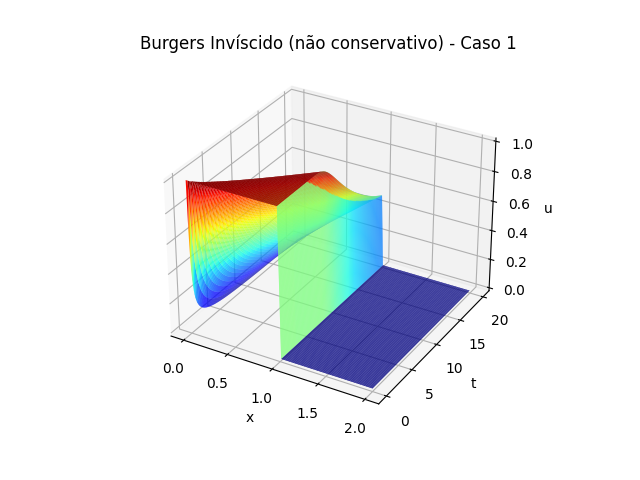
plot3D(200, u_nc, 2, 4, 2, 100, title, 0) | |||
u_c, x_c = burgCons(nt, 100, 4, 2) | |||
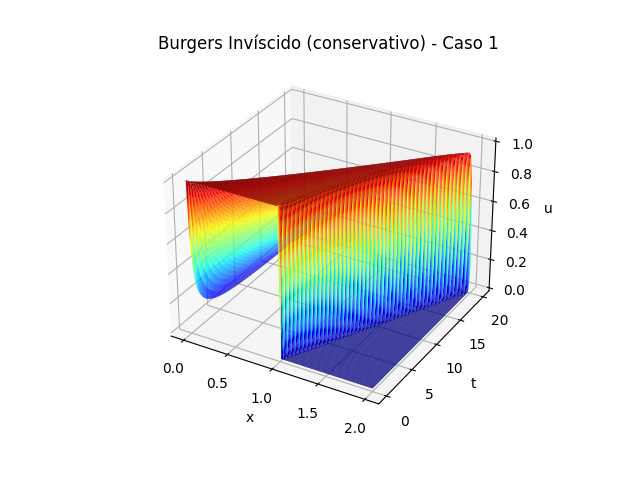
title = 'Burgers Invíscido (conservativo) - Caso 1' | |||
plot3D(200, u_c, 2, 4, 2, 100, title, 1) | |||
</source> | |||
==== Como Resultado ==== | |||
<gallery class="center" mode=packed heights=350px> | |||
U_inv_nc.png|Gráfico 3D da solução da equação de Burgers para o caso invíscido com método FTCS não conservativo. | |||
U_inv_con.png|Gráfico 3D da solução da equação de Burgers para o caso invíscido com método FTCS conservativo. | |||
</gallery> | |||
É possível observar o comportamento discutido acima, quando <math>\nu=0</math> a descontinuidade não se propaga pelo método FTCS não conservativo; em oposição ao método conservativo, onde se propaga. | |||
== Apêndice == | == Apêndice == | ||
O limite bilateral da função não existe no ponto na qual é centrada (assim como a função [https://en.wikipedia.org/wiki/Heaviside_step_function degrau de Heavisde]). Dessa forma, pode-se calcular o os dois limites unilaterais para entender o comportamento da função, assim: | O limite bilateral da função não existe no ponto na qual é centrada (assim como a função [https://en.wikipedia.org/wiki/Heaviside_step_function degrau de Heavisde]). Dessa forma, pode-se calcular o os dois limites unilaterais para entender o comportamento da função, assim: | ||
<math>\lim _{ | <math>\lim _{\nu \rightarrow 0^{-}}\left(\frac{u_{D}+u_{E}}{2}-\frac{1}{2}(u_{E}-u_{D}) \tanh \left(\frac{y(u_{E}-u_{D})}{4 \nu}\right)\right) \text{ para } u_{D}<u_{E}</math> | ||
<math>\lim _{ | <math>\lim _{\nu \rightarrow 0^{-}}\left(\frac{u_{E}+u_{D}}{2}-\frac{1}{2}(u_{E}-u_{D}) \tanh \left(\frac{y(u_{E}-u_{D})}{4 \nu}\right)\right)</math> | ||
<math>\lim _{ | <math>\lim _{\nu \rightarrow 0^{-}}\left(\frac{u_{E}+u_{D}}{2}-\frac{1}{2} \tanh \left(\frac{y(u_{E}-u_{D})}{4 \nu}\right)(u_{E}-u_{D})\right)</math> | ||
<math>\lim _{ | <math>\lim _{\nu \rightarrow 0^{-}}-\frac{1}{2} \tanh \left(\frac{y(u_{E}-u_{D})}{4 \nu}\right)(u_{E}-u_{D})+\left(\frac{u_{E}+u_{D}}{2}\right)</math> | ||
Aplicando a regra do produto: | Aplicando a regra do produto: | ||
<math>\frac{\lim _{ | <math>\frac{\lim _{\nu \rightarrow 0^{-}} \tanh \left(\cfrac{y(u_{E}-u_{D})}{4 \nu}\right)(-u_{E}+u_{D})}{2}+\frac{u_{E}+u_{D}}{2}</math> | ||
<math>\lim _{ | <math>\lim _{\nu \rightarrow 0^{-}} \tanh \left(\frac{y(u_{E}-u_{D})}{4 \nu}\right)=-1 \text{ para } u<u_{E} </math> | ||
<math>\frac{u_{E}-u_{D}}{2}+\frac{u_{E}+u_{D}}{2}=u_{E} \text{ para } u_{D}<u_{E} \implies \lim _{ | <math>\rightarrow \frac{u_{E}+u_{D}}{2}+\frac{(-u_{E}+u_{D})(-1)}{2}=\frac{u_{E}-u_{D}}{2}+\frac{u_{E}+u_{D}}{2}</math> | ||
<math>\frac{u_{E}-u_{D}}{2}+\frac{u_{E}+u_{D}}{2}=u_{E} \text{ para } u_{D}<u_{E} </math> | |||
<math>\implies \lim _{\nu \rightarrow 0^{-}}\left(\frac{u_{D}+u_{E}}{2}-\frac{1}{2}(u_{E}-u_{D}) \tanh \left(\frac{y(u_{E}-u_{D})}{4 \nu}\right)\right)=u_{E} \text{ para } u_{D}<u_{E}</math> | |||
Para o segundo caso: | Para o segundo caso: | ||
<math>\lim _{ | <math>\lim _{\nu \rightarrow 0^{+}}\left(\frac{u_{E}+u_{D}}{2}-\frac{1}{2}(u_{E}-u_{D}) \tanh \left(\frac{y(u_{E}-u_{D})}{4 \nu}\right)\right)</math> | ||
<math>\lim _{ | <math>\lim _{\nu \rightarrow 0^{+}}\left(\frac{u_{E}+u_{D}}{2}-\frac{1}{2} \tanh \left(\frac{y(u_{E}-u_{D})}{4 \nu}\right)(u_{E}-u_{D})\right)</math> | ||
<math>\lim _{ | <math>\lim _{\nu \rightarrow 0^{+}}-\frac{1}{2} \tanh \left(\frac{y(u_{E}-u_{D})}{4 \nu}\right)(u_{E}-u_{D})+\left(\frac{u_{E}+u_{D}}{2}\right)</math> | ||
Aplicando a regra do produto: | Aplicando a regra do produto: | ||
<math>\frac{\lim _{ | <math>\frac{\lim _{\nu \rightarrow 0^{+}} \tanh \left(\cfrac{y(u_{E}-u_{D})}{4 \nu}\right)(-u_{E}+u_{D})}{2}+\frac{u_{E}+u_{D}}{2}</math> | ||
<math>\lim _{\nu \rightarrow 0^{+}} \tanh \left(\frac{y(u_{E}-u_{D})}{4 \nu}\right)=1 \text{ para } u_{D}<u_{E} </math> | |||
<math>\rightarrow \frac{u_{E}+u_{D}}{2}+\frac{(-u_{E}+u_{D})(1)}{2}=\frac{u_{E}+u_{D}}{2}+\frac{u_{D}-u_{E}}{2}</math> | |||
<math> | <math>\frac{u_{E}+u_{D}}{2}+\frac{u_{D}-u_{E}}{2}=u_{D} \text{ para } u_{D}<u_{E} </math> | ||
<math> | <math>\implies \lim _{\nu \rightarrow 0^{+}}\left(\frac{u_{E}+u_{D}}{2}-\frac{1}{2}(u_{E}-u_{D}) \tanh \left(\frac{y(u_{E}-u_{D})}{4 \nu}\right)\right)=u_{D} \text{ para } u_{D}<u_{E}</math> | ||
Ao analisar gráfico, verifica-se esse comportamento. | Ao analisar gráfico, verifica-se esse comportamento (ver [[#Gráfico|figura 2]]).. | ||
== Referências == | == Referências == | ||
<references/> | <references/> | ||
Edição atual tal como às 20h27min de 12 de outubro de 2021
Grupo: Eduardo Pedroso, Luis Gustavo Lang Gaiato e William Machado Pantaleão
Um dos maiores desafios no campo dos sistemas complexos é a compreensão do fenômeno de turbulência. Simulações computacionais contribuíram bastante para o entendimento dessa área, no entanto, ainda não existe nenhuma teoria que explique com sucesso esse comportamento e permita prever outros importantes fenômenos como misturas, convecção e combustão turbulentas, com base nas equações fundamentais da dinâmica de fluidos. Isso se deve ao fato de que a equação para os fluidos mais simples (incompressíveis) já deve levar em consideração propriedades não lineares [1]. Da equação de Navier–Stokes:
Devido à incompressibilidade, a pressão é definida pela equação de Poisson:
Em 1939 o cientista alemão Johannes Martinus Burgers simplificou a equação de Navier-Stokes, removendo o termo de pressão. A equação ficou conhecida como equação de Burgers. Em uma dimensão, onde corresponde ao campo de velocidades e ao coeficiente de difusão:
A equação de Burgers é não linear e, portanto, espera-se um comportamento similar ao da turbulência. No entanto, foi demonstrado posteriormente que a equação de Burgers homogênea, não possuí a propriedade mais importante atribuída ao fenômeno de turbulência: o comportamento caótico em relação à pequenas mudanças nas condições iniciais. Utilizando a transformação de Hopf-Cole, que transforma a equação de Burgers em uma equação parabólica linear é possível observar essa característica [2].
Do ponto de vista numérico, isso é bastante importante, pois permite a comparação das soluções da equação não linear numérica com o resultado analítico. Dessa forma, pode-se investigar a qualidade do método numérico utilizado.
A transformação de Hopf-Cole
A transformação de Hopf-cole mapeia a solução da equação de Burgers na equação do calor [2] [3] [4]:
Escrevendo a equação, para uma certa condição inicial :
Assim, reescrevendo a equação:
Busca-se uma solução que satisfaça:
Como:
Tem-se, que:
Aplicando a transformação de Hopf-Cole:
Assim, os seguintes resultados são obtidos:
Dessa forma:
A equação se torna a própria equação de difusão. É necessário, no entanto, transformar também as condições de contorno; assim:
Podendo ser reescrito como:
Cuja solução:
Dessa forma, é preciso resolver:
Utilizando a transformada de Fourier:
Cuja solução:
Aplicando o teorema da convolução:
Onde:
Em :
Onde:
Modelo de Deposição - Crescimento de Interfaces

Um exemplo de aplicação é no crescimento de interfaces por deposição, já que a equação de Burgers é equivalente a equação conhecida como, equação de Kardar-Parisi-Zhang (equação KPZ), um modelo de crescimento de uma superfície sólida por deposição de vapor (ou erosão de material de uma superfície sólida), que mostra a evolução da altura da camada com o tempo [6].
A equação é obtida a partir da equação de advecção simples para uma superfície se movimentando com velocidade :
A velocidade é assumida como sendo proporcional ao gradiente de (superfície evolui na direção do gradiente). A difusão da superfície é descrita pelo termo de difusão.
A equação KPZ unidimensional corresponde a versão estocástica da equação de Burgers com campo pela substituição .
Solução de Onda Viajante
Pode-se ainda, encontrar uma solução para a equação de Burgers na forma de uma onda viajante. Assim:
Dessa forma:
Substituindo na equação de Burgers:
Impondo condições em , tais que:
Onde . Dessa forma, tem-se que:
Desse modo, a velocidade de choque é a mesma para o caso de viscosidade nula . Continuando:
Integrando ambas as partes, utilizando que:
Utilizando o fato de que :
Portanto:
Onde:
Multiplicando e dividindo por :
Dessa forma:
Portanto:
Gráfico
O perfil da função pode ser plotado para diferentes viscosidades. Sabe-se, que conforme a viscosidade se aproxima de zero (fluido invíscido) a função se aproxima de uma função degrau de argumento (ver Apêndice).
O gráfico pode ser construido utilizando o código em Python abaixo.
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from matplotlib.animation import FuncAnimation
from matplotlib.lines import Line2D
import numpy as np
from numpy import ndarray
from typing import Any
u, v, x0 = 0, 1, 0 # define-se os parametros iniciais u=u_D, v=u_E
def w(y:ndarray, nu:float): # funcao w(y)
arg = (y*(v-u))/(4*nu)
return((u+v)/2 - ((v-u)/2) *np.tanh(arg))
fig = plt.figure(figsize=(12.8, 3.7), dpi=80) # resolucao da gráfico
ax = plt.axes(xlim=(-2, 2), ylim=(0, 1), # características dos eixos
xlabel=r'$y$', ylabel=r'$w(y)$')
line, = ax.plot([], [], lw=3) # cria-se um obejto 'Line' de 2D
plt.title('Perfis da Equação '+r'$w(y)$'+ # titulo do grafico
' para Diferentes Viscosidades')
def init(): # funcao que inicia a animacao caso o frame=0 seja vazio
line.set_data([], [])
return line,
def animate(frame, *fargs: Any) -> tuple[Line2D]: # função que plota os gráficos
c = 0 # inicializa a variavel
y = np.linspace(-2,2,100) # cria um array de valores para y
nu_list = np.linspace(0.4,0.02,50) # cria um array de valores de viscosidade
w_arr = w(y, nu_list[frame]) # cria o array de w(y, nu)
colour = iter(cm.rainbow(np.linspace(0,2,110))) # iteravel utilizado para as cores
for k in range(frame + 1): # avanca o objeto iteravel em (frame + 1) vezes
c = next(colour)
plt.plot(y, w_arr, color=c) # faz com que as linhas sejam mantidas entre frames
ax.text(1, 0.9, r'$\nu = $'+f'{nu_list[frame]:.3f}', fontsize=15, # adiciona nu
bbox=dict(edgecolor='white', facecolor='white', alpha=1))
line.set_color(c) # define a cor da linha com base no iteravel atualizado
line.set_data(y, w_arr) # define o novo conjunto de dados
return(line,) # retorna o objeto iteravel [Linha2D]
anim = FuncAnimation(fig, animate, init_func=init, # funcao que produz a animacao
frames=50, interval=100, blit=True) # 50 frames com intervalo de 0.1s
anim.save('shockwaveee.gif', writer='imagemagick') # gera um .GIF (e renderizacao)
Velocidade de Choque
Tomando a viscosidade como nula, a equação de Burgers pode ser reescrita como[7]:
Cuja solução é dada na forma e uma onda viajante:
Onde é uma função degrau:
Onde . Essa onda é chamada de onda de choque, e possui velocidade de propagação . Por conservação, a condição de salto:
Por outro lado:
Portanto:
Dessa forma:
O caso generalizado da velocidade de propagação de uma onda de choque é conhecido como condição de Rankine-Hugoniot, e pode ser obtido, desse resultado, pela aplicação das leis de conservação hiperbólicas:
Assim:
A condição de Rankine-Hugoniot, onde o salto da função é definido como choque.
Métodos Numéricos
Discretizando a equação de Burgers para um fluido víscido, a partir da abordagem FTCS (Foward Time Central Space), com a derivada à direita:
Se:
Conservação
Um dos problemas no cálculo de soluções descontinuas para equações como a de Burgers pode ser exemplificado da seguinte forma; supondo a equação de Burgers na forma quasi-linear com viscosidade nula:[7]
Com condições iniciais:
Pela discretização feita anteriormente:
Pelas condições iniciais, para e para :
Como resultado, . Dessa forma, ; isso significa que o método propaga a descontinuidade (onda de choque) com a velocidade incorreta, ; ou seja, não ocorre propagação após o choque.
Método Conservativo
A partir da discretização para o caso víscido, se , então:
Assim como para o caso anterior, esse método não é conservativo e é adequado apenas para soluções que não possuem descontinuidades. Considerando a lei de conservação:
Discretizando:
Onde a função corresponde à uma função de argumentos, chamada de fluxo numérico [7] [8] [9]. Assim, para e , :
Lax-Friedrichs
O método de Lax-Friedrichs para sistemas não lineares possui a forma:
Para o caso da equação de Burgers invíscida:
Lax-Wendroff
O método de Lax-Wendroff é um método de segunda ordem e possui a forma [9][8]:
Onde corresponde à matriz jacobiana , avaliada em . Para a equação de Burgers (invíscida) , assim:
Método parabólico
Considerando a equação de Burgers víscida com , na forma [8]:
Integrando de até :
Aproximando-se cada termo da equação acima tem-se que, para o primeiro termo:
Para o segundo:
Para o terceiro:
Substituindo as aproximações na expressão completa e definindo :
Discretizando a derivada em relação a tempo por um método FTCS:
Onde é calculada numericamente como a média entre e .
Implementação
Foram implementados quatro métodos: para o caso víscido, FTCS não conservativo e o método parabólico; para o caso invíscido, FTCS não conservativo e FTCS conservativo. Definindo a condição de contorno periódica , e utilizando as condições iniciais:
Caso 1:
Caso 2:
Derivando e substituindo na equação:
Cuja solução analítica é
Derivando e substituindo na equação:
Importando os Módulos Utilizados
# -*- coding: utf-8 -*-
from math import pi, exp
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
Array2D = np.ndarray # typing...
Burgers FTCS Víscido Não Conservativo
def burgers(nt:int, nx:int, tmax:float, xmax:float, v:float, caso:int) -> tuple:
# incrementos
dt = tmax/(nt-1) # no tempo
dx = xmax/(nx-1) # no espaco
# arrays
u = np.zeros((nx, nt)) # velocidade
x = np.zeros(nx)
ipos = np.zeros(nx)
ineg = np.zeros(nx)
# condicoes de contorno periodicas
for i in range(0, nx): # i: 0, 1, ... nx-2, nx-1, nx
x[i] = i*dx
ipos[i] = i+1 # 1, 2, ... nx-2, nx+1
ineg[i] = i-1 # -1, 0, ... nx-2, nx-1
ipos[-1] = 0 # ipos[nx-1] = 0, u_{n+1}
ineg[0] = nx-1 # u_{n-1}
# condicoes iniciais
if caso == 1:
for i in range(0,nx):
if x[i] <= 1:
u[i,0] = 1
elif x[i] > 1:
u[i,0] = 0
elif caso == 2:
for i in range(0, nx):
phi = exp( -(x[i]**2)/(4*v) ) + exp( -(x[i]-2*pi)**2 / (4*v) )
dphi = (-(0.5*x[i]/v)*exp( -(x[i]**2) / (4*v) ) - (0.5*(x[i]-2*pi) / v )
*exp(-(x[i]-2*pi)**2 / (4*v) ))
u[i,0] = -2*v*(dphi/phi) + 4
# solucao numerica
for n in range(0, nt-1):
for i in range(0,nx):
u[i,n+1] = (u[i,n]-u[i,n]*(dt/dx)*(u[i,n]-u[int(ineg[i]),n])+
v*(dt/dx**2)*(u[int(ipos[i]),n]-2*u[i,n]+u[int(ineg[i]),n]))
return((u, x))
Burgers Víscido Parabólico
def burgParab(nt:int, nx:int, tmax:float, xmax:float, v:float, caso:int) -> tuple:
def f(u):
return((u**2)/2)
# incrementos
dt = tmax/(nt-1)
dx = xmax/(nx-1)
# arrays
u = np.zeros((nx,nt))
x = np.zeros(nx)
ipos = np.zeros(nx)
ineg = np.zeros(nx)
# condicoes de contorno periodicas
for i in range(0,nx):
x[i] = i*dx
ipos[i] = i+1
ineg[i] = i-1
ipos[nx-1] = 0
ineg[0] = nx-1
# condicoes iniciais
if caso == 1:
for i in range(0,nx):
if x[i] <= 1:
u[i,0] = 1
elif x[i] > 1:
u[i,0] = 0
elif caso == 2:
for i in range(0,nx):
phi = exp( -(x[i]**2)/(4*v) ) + exp( -(x[i]-2*pi)**2 / (4*v) )
dphi = (-(0.5*x[i]/v)*exp( -(x[i]**2) / (4*v) ) - (0.5*(x[i]-2*pi) / v )
*exp(-(x[i]-2*pi)**2 / (4*v) ))
u[i,0] = -2*v*(dphi/phi) + 4
# solucao numerica
for n in range(0,nt-1):
for i in range(0,nx):
fminus = 0.5*(f(u[i,n]) + f(u[int(ineg[i]),n]))
fplus = 0.5*(f(u[i,n]) + f(u[int(ipos[i]),n]))
u[i,n+1] = u[i,n]+dt*(v*((u[int(ipos[i]),n]-(2*u[i,n])+u[int(ineg[i]),n])/(dx**2))-(fplus-fminus)/dx)
return((u, x))
Burgers Víscido Analítico (Caso 2)
def burgers_analytical(nt:int, nx:int, tmax:float, xmax:float, v:float) -> tuple:
# incrementos
dt = tmax/(nt-1)
dx = xmax/(nx-1)
# arrays
u_a = np.zeros((nx, nt))
x = np.zeros(nx)
t = np.zeros(nt)
# len(x)
for i in range(0, nx):
x[i] = i*dx
# solucao analitica
for n in range(0, nt):
t = n*dt
for i in range(0, nx):
phi = (exp( -(x[i]-4*t)**2/(4*v*(t+1)) ) +
exp( -(x[i]-4*t-2*pi)**2/(4*v*(t+1)) ))
dphi = ( -0.5*(x[i]-4*t)/(v*(t+1))*exp( -(x[i]-4*t)**2/(4*v*(t+1)) )
-0.5*(x[i]-4*t-2*pi)/(v*(t+1))*exp( -(x[i]-4*t-2*pi)**2/(4*v*(t+1)) ) )
u_a[i,n] = -2*v*(dphi/phi) + 4
return((u_a, x))
Burgers FTCS Invíscido Não Conservativo
def burgInv(nt:int, nx:int, tmax:float, xmax:float) -> tuple:
# incrementos
dt = tmax/(nt-1)
dx = xmax/(nx-1)
# arrays
u = np.zeros((nx,nt))
x = np.zeros(nx)
ipos = np.zeros(nx)
ineg = np.zeros(nx)
# condicoes de contorno periodicas
for i in range(0,nx):
x[i] = i*dx
ipos[i] = i+1
ineg[i] = i-1
ipos[nx-1] = 0
ineg[0] = nx-1
# condicoes iniciais
for i in range(0,nx):
if x[i]<=1:
u[i,0] = 1
elif x[i]>1:
u[i,0] = 0
# solucao numerica
for n in range(0,nt-1):
for i in range(0,nx):
u[i,n+1] = (u[i,n]-u[i,n]*(dt/dx)*(u[i,n]-u[int(ineg[i]),n]))
return((u, x))
Burgers FTCS Invíscido Conservativo
def burgCons(nt:int, nx:int, tmax:float, xmax:float) -> tuple:
# incrementos
dt = tmax/(nt-1)
dx = xmax/(nx-1)
# arrays
u = np.zeros((nx,nt))
x = np.zeros(nx)
ipos = np.zeros(nx)
ineg = np.zeros(nx)
# condicoes de contorno periodicas
for i in range(0,nx):
x[i] = i*dx
ipos[i] = i+1
ineg[i] = i-1
ipos[nx-1] = 0
ineg[0] = nx-1
# condicoes iniciais
for i in range(0,nx):
if x[i]<=1:
u[i,0] = 1
elif x[i]>1:
u[i,0] = 0
# solucao numerica
for n in range(0,nt-1):
for i in range(0,nx):
u[i,n+1] = (u[i,n]-(dt/dx)*((1/2 * (u[i,n])**2)-(1/2 * (u[int(ineg[i]),n])**2)))
return((u, x))
Gráfico de e vs.
def plot(u_a:Array2D, u:Array2D, x:list, nt:int, title:str):
plt.figure(figsize=(8, 6), dpi=80)
colour=iter(cm.rainbow(np.linspace(0, 20, nt)))
for n in range(0, nt, 20):
c=next(colour)
plt.plot(x, u[:, n], 'ko', markerfacecolor=c, alpha=0.5)
plt.plot(x, u_a[:, n], linestyle='-', c=c, label=f'i={n}')
plt.legend()
plt.xlabel(r'$x$')
plt.ylabel(r'$u$')
plt.ylim([0, 8.0])
plt.xlim([0, max(x)])
plt.title(title)
plt.show()
Gráfico de , e vs. na Última Iteração
def plotErro(u:Array2D, u_p:Array2D, u_a:Array2D, x:list, v:float):
plt.plot(x, u[:,-10], label='Burgers', color='blue')
plt.plot(x, u_a[:,-10], label='Analítico', color='red')
plt.plot(x, u_p[:,-10], label='Parabólico', color='green')
plt.legend()
plt.xlabel(r'$x$')
plt.ylabel(r'$u$')
plt.title('Última Interação com ' + r'$\nu=$' + f'{v}')
plt.show()
Gráfico 3D Invíscido (Caso 1)
def plot3D(num:int, arr:Array2D, xmax:int, tmax:int, n:int, nx:int, title:str, cond:int) -> None:
w_arr = np.zeros((num,len(arr[:,-1])))
x_arr = np.zeros((num,len(arr[:,-1])))
for i in range(num):
if cond == 0:
w, x_res = burgInv(nt, nx, n*i/num, xmax)
elif cond == 1:
w, x_res = burgCons(nt, nx, n*i/num, xmax)
elif cond == 2:
w, x_res = burgParab(nt, nx, n*i/num, xmax, 0.1,2)
elif cond == 3:
w, x_res = burgers(nt, nx, n*i/num, xmax, 0.1, 2)
w_arr[i] = w[:,-1]
x_arr[i] = x_res
ax = plt.axes(projection='3d')
times = np.zeros((num,1))
t = 0
dt = 0
for i in range(num):
times[i,0] = t + dt
dt += tmax/num
ax.plot_surface(x_arr, times, w_arr, rstride=1, cstride=1,
cmap='jet', edgecolor='none')
plt.title(title)
ax.set_xlabel('x')
ax.set_ylabel('t')
ax.set_zlabel('u')
plt.show()
Exemplo de Utilização
Define-se , , , e :
nt, nx, tmax, xmax, v = 200, 200, 0.5, 2*pi, 0.1
Chama-se as funções de cálculo e constrói os gráficos:
u, x = burgers(nt, nx, tmax, xmax, v, 2) # ftcs nao conservativo
u_a, x = burgers_analytical(nt, nx, tmax, xmax, v) # ftcs analítico
u_p, x = burgParab(nt, nx, tmax, xmax, v, 2) # # ftcs parabolico
title = str(r'($\nu=$'+f'{v}, '+r'$n_t$'+f'={nt}, '+
r'$n_x$'+f'={nx}, '+r'$t_{max}$'+f'={tmax})')
plot(u_a, u, x, nt, 'Não Conservativo ' + title) # grafico de u e u_a vs. x
plot(u_a, u_p, x, nt, 'Parabólico ' + title) # grafico de u_p e u_a vs. x
plotErro(u, u_p, u_a, x, v)
Como Resultado
É possível observar que o método não conservativo propaga a descontinuidade com velocidade incorreta, ao contrário do método parabólico. De fato, como demonstrado anteriormente (ver Conservação), no caso em que , pelo método não conservativo a velocidade é nula.
Para o Caso Invíscido
u_nc, x_nc = burgInv(nt, 100, 4, 2)
title = 'Burgers Invíscido (não conservativo) - Caso 1'
plot3D(200, u_nc, 2, 4, 2, 100, title, 0)
u_c, x_c = burgCons(nt, 100, 4, 2)
title = 'Burgers Invíscido (conservativo) - Caso 1'
plot3D(200, u_c, 2, 4, 2, 100, title, 1)
Como Resultado
É possível observar o comportamento discutido acima, quando a descontinuidade não se propaga pelo método FTCS não conservativo; em oposição ao método conservativo, onde se propaga.
Apêndice
O limite bilateral da função não existe no ponto na qual é centrada (assim como a função degrau de Heavisde). Dessa forma, pode-se calcular o os dois limites unilaterais para entender o comportamento da função, assim:
Aplicando a regra do produto:
Para o segundo caso:
Aplicando a regra do produto:
Ao analisar gráfico, verifica-se esse comportamento (ver figura 2)..
Referências
- ↑ F. M. White, Viscous Fluid Flow, 3rd ed. New York, NY: McGraw-Hill Professional, 2005.
- ↑ 2,0 2,1 Hopf, E. (1950). The partial differential equation ut + uux = μxx. Communications on Pure and Applied Mathematics, 3(3), 201–230. doi:10.1002/cpa.3160030302
- ↑ Evans, Lawrence C. (2010). Partial differential equations. [S.l.]: Providence, R.I. : American Mathematical Society. pp. 175–176
- ↑ Meylan, M., 2020. Nonlinear PDE Meylan. Lecture 12. [online] Youtube.com. Disponível em: <https://youtu.be/CsnUKrLjtyQ> [Acessado em 30 Setembro de 2021]
- ↑ Halpin-Healy, T., 2015. KPZ growth model - ballistic deposition (BD). [online] Youtube.com. Disponível em: <https://youtu.be/pdeswgu9rS8> [Acessado em 30 Setembro de 2021]
- ↑ Reis, F. D. A. A. Depinning transitions in interface growth models. Brazilian journal of physics, v. 33, n. 3, p. 501–513, 2003
- ↑ 7,0 7,1 7,2 Cameron, M. Notes on Burgers's Equation. University of Maryland, 2021
- ↑ 8,0 8,1 8,2 Landajuela, M. Burgers Equation. Basque Center for Applied Mathematics, 2011
- ↑ 9,0 9,1 LeVeque, Randall J. (1992). Numerical Methods for Conservation Laws (PDF). Boston: Birkhäuser. p. 125. ISBN 0-8176-2723-5.



















![{\displaystyle {\frac {\partial \psi }{\partial t}}=\nu {\frac {\partial ^{2}\psi }{\partial x^{2}}}-{\frac {1}{2}}\left({\frac {\partial \psi }{\partial x}}\right)^{2}\rightarrow -{\frac {2\nu }{\phi }}\left({\frac {\partial \phi }{\partial t}}\right)={\frac {2\nu ^{2}}{\phi ^{2}}}\left({\frac {\partial \phi }{\partial x}}\right)^{2}-{\frac {2\nu ^{2}}{\phi }}\left({\frac {\partial ^{2}\phi }{\partial x^{2}}}\right)-{\frac {1}{2}}\left[{\frac {2\nu }{\phi }}\left({\frac {\partial \phi }{\partial x}}\right)\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59502a7281885756c7c6e7e64f382da4675e7ed3)







![{\displaystyle \phi (x,t)=\Phi (x){\mathcal {F}}^{-1}\left[e^{-k^{2}\nu t}\right]={\frac {1}{2{\sqrt {\pi \nu t}}}}\int _{-\infty }^{\infty }\Phi (y)e^{\frac {(x-y)^{2}}{4\nu t}}dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/becee279c3709535e225d8268c278d4f523274d8)































![{\displaystyle {\frac {u_{E}-w}{w-u_{D}}}=\exp {\left[{{\frac {y\left(u_{E}-u_{D}\right)}{2\nu }}+C}\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2183db76992c4d110bfc49a9d26456509e1f8d70)







































![{\displaystyle U_{i}^{n+1}=U_{i}^{n}-{\frac {\Delta t}{\Delta x}}\left[f\left(U_{i}^{n}\right)-f\left(U_{i-1}^{n}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/575f77ec7bac9af99d3d6a6c1214bffb2a6a082f)





![{\displaystyle U_{i}^{n+1}=U_{i}^{n}-{\frac {\Delta t}{\Delta x}}\left[{\frac {1}{2}}\left(U_{i}^{n}\right)^{2}-{\frac {1}{2}}\left(U_{i-1}^{n}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e8867656f5eb369dc22ffbd708e9dc7b6784ad5)
![{\displaystyle U_{i}^{n+1}={\frac {1}{2}}\left(U_{i-1}^{n}+U_{i+1}^{n}\right)-{\frac {k}{2h}}\left[f\left(U_{i+1}^{n}\right)-f\left(U_{i-1}^{n}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/433340aee81e8b3823f418097653646b801fc0de)
![{\displaystyle U_{i}^{n+1}={\frac {1}{2}}\left(U_{i-1}^{n}+U_{i+1}^{n}\right)-{\frac {\Delta t}{2\Delta x}}\left[{\frac {1}{2}}\left(U_{i+1}^{n}\right)^{2}-{\frac {1}{2}}\left(U_{i-1}^{n}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e34c008cdb9ef4354fb18390247e36bc15f514c3)
![{\displaystyle U_{i}^{n+1}=U_{i+1}^{n}-{\frac {k}{2h}}\left(f\left(U_{i+1}^{n}\right)-f\left(U_{i-1}^{n}\right)\right)+{\frac {k^{2}}{2h^{2}}}\left[A_{i+{\frac {1}{2}}}\left(f\left(U_{i+1}^{n}\right)-f\left(U_{i}^{n}\right)\right)-A_{i-{\frac {1}{2}}}\left(f\left(U_{i}^{n}\right)-f\left(U_{i-1}^{n}\right)\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/237a20f190ff0cfc285c7c5988a2bfc053947da6)





![{\displaystyle {\frac {k^{2}}{2h^{2}}}\left[\left({\frac {1}{2}}\left(U_{i}^{n}+U_{i+1}^{n}\right)\right)\left({\frac {1}{2}}\left(U_{i+1}^{n}\right)^{2}-{\frac {1}{2}}\left(U_{i}^{n}\right)^{2}\right)-\left({\frac {1}{2}}\left(U_{i}^{n}+U_{i-1}^{n}\right)\right)\left({\frac {1}{2}}\left(U_{i}^{n}\right)^{2}-{\frac {1}{2}}\left(U_{i-1}^{n}\right)^{2}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d46837e7104a7619b6d9cadfc2fe96bc44e04af)




![{\displaystyle \int _{x_{i-1/2}}^{x_{i+1/2}}{\frac {\partial u}{\partial t}}dx-\left[\nu {\frac {\partial u}{\partial x}}\right]_{x_{i-1/2}}^{x_{i+1/2}}=-[f(u)]_{x_{i-1/2}}^{x_{i+1/2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/294f0c858721a3b18436c8b5d29b35e2e9767ece)

![{\displaystyle -\left[\nu {\frac {\partial u}{\partial x}}\right]_{x_{i-1/2}}^{x_{i+1/2}}=\nu \left[{\frac {\partial u}{\partial x}}\left(x_{i-1/2},t\right)-{\frac {\partial u}{\partial x}}\left(x_{i+1/2},t\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9766fb3d61369fb193875d5402bfdc16a2b965b)
![{\displaystyle \implies -\left[\nu {\frac {\partial u}{\partial x}}\right]_{x_{i-1/2}}^{x_{i+1/2}}\approx \nu \left[{\frac {u\left(x_{i},t\right)-u\left(x_{i-1},t\right)}{h}}-{\frac {u\left(x_{i+1},t\right)-u\left(x_{i},t\right)}{h}}\right]=-\nu {\frac {u\left(x_{i+1},t\right)-2u\left(x_{i},t\right)+u\left(x_{i-1},t\right)}{h}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f7edbfe0e9d24d230fcdb6ae8e96bf306fb727d)
![{\displaystyle -[f(u)]_{x_{i-1/2}}^{x_{i+1/2}}=f\left(u\left(x_{i-1/2},t\right)\right)-f\left(u\left(x_{i+1/2},t\right)\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db7eecd175d17e48f6ce953bdbdac7b6ec454a13)








![{\displaystyle \left\{{\begin{array}{l}u_{i}^{n=0}={\frac {-2\nu }{\phi (x,\nu )}}\left({\frac {\partial \phi (x,\nu )}{\partial x}}\right)+4\\\phi =e^{\left({\frac {-x^{2}}{4\nu }}\right)+e^{\left[{\frac {-(x-2\pi )^{2}}{4\nu }}\right]}}\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97d75d5093d652706b06df988f361b809a0fc456)

![{\displaystyle \implies u_{i}^{n=0}=-{\cfrac {x}{2\nu }}e^{\left({\cfrac {-x^{2}}{4\nu }}\right)}-{\cfrac {(x-2\pi )}{2\nu }}e^{\left[{\cfrac {-(x-2\pi )^{2}}{4\nu }}\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b439515ec7f4570fe35a55093aeafe46d3e87661)
![{\displaystyle \left\{{\begin{array}{l}u_{i}^{n}={\frac {-2\nu }{\phi (x,\nu )}}\left({\frac {\partial \phi (x,\nu )}{\partial x}}\right)+4\\\phi =e^{\left({\frac {-(x-4t)^{2}}{4\nu (t+1)}}\right)+e^{\left[{\frac {-(x-4t-2\pi )^{2}}{4\nu (t+1)}}\right]}}\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9e614c81dbb77c72906d50738dfa21e0feba4c9)
![{\displaystyle u_{i}^{n}=-{\frac {(x-4t)}{2\nu (t+1)}}e^{-\left({\frac {(x-4t)^{2}}{4\nu (t+1)}}\right)}-{\frac {(x-4t-2\pi )}{2\nu (t+1)}}e^{\left[{\frac {-(x-4t-2\pi )^{2}}{4\nu (t+1)}}\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14b5d5dc18c9b23425e12fbf223c3a336e7bea20)