Clusterização: mudanças entre as edições
| (17 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
'''PÁGINA EM CONSTRUÇÃO''' | '''PÁGINA EM CONSTRUÇÃO''' | ||
== Clusterização do Modelo de Ising == | == Clusterização do Modelo de Ising == | ||
=== | O modelo de Ising é definido como uma malha de tamanho L, quadrada quando em duas dimensões e cúbica quando em três dimensões, onde cada vértice apresenta um componente de spin de magnitude fixa que pode apontar para cima ou para baixo (+1 ou -1, respectivamente). O sistema pode ser descrito pelo seguinte hamiltoniano: | ||
<math>H_{Ising} = -J \sum_{\langle ij \rangle} s_i s_j</math> | |||
onde <math>s</math> representa o valor do spin e a soma é feita sobre os pares de vértices próximas que são conectadas com um acoplamento ferromagnético de força <math>J > 0</math>. | |||
Para um modelo de Ising bidimensional (o tipo que consideramos) é possível calcular [1] sua temperatura crítica exata como: | |||
<math>T_c = \frac{2J}{\log(1 + \sqrt{2})} \simeq 2.269J</math> | |||
Acima dessa temperatura o sistema está na ‘’’fase paramagnética‘’’, onde a magnetização média é nula, e abaixo dessa temperatura o sistema está na fase ‘’’fase ferromagnética’’’, onde a maioria dos spins se alinham e a magnetização se torna não-nula. Ao estudar o modelo de Ising em geral temos maior interesse no comportamento do sistema perto de <math>T_c</math>, onde o sistema forma grupos grandes de spins para cima ou para baixo. Esses grupos contribuem muito para a energia do sistema, causando muita flutuação quando invertem. | |||
O algoritmo de Metropolis é um ótimo algoritmo para realizar simulações do modelo de Ising [1]. Porém, sua dinâmica de ''flip'' único é ineficiente especialmente quando próxima da temperatura crítica do sistema. As imprecisões estatísticas de quantidades como magnetização e energia interna do sistema aumentam quando próximo da temperatura crítica. Assim, quando esses grandes grupos de spins alinhados (clusters) invertem, há grandes imprecisões. Essa imprecisão aumenta com o tamanho das flutuações, mas diminui com o número de medidas feitas na simulação, então para se estudar a região perto de <math>T_c</math> de modo mais preciso é necessário que a simulação aconteça por mais tempo. Porém, uma outra fraqueza do algoritmo de Metropolis é seu tempo de correlação <math>\tau</math> grande ao redor da temperatura crítica. Isso significa que o número de medidas de uma simulação é pequena, então para diminuir as imprecisões estatísticas causadas pelas poucas medidas é necessário rodar o algoritmo por mais tempo. | |||
Uma das propriedades do modelo de Ising é o fato de flutuações grandes gerarem medidas mais imprecisas. Porém, o tempo de correlação e o modo como ele se comporta próximo a <math>T_c</math> é uma propriedade do algoritmo utilizado para estudar o sistema, e então é algo que pode ser otimizado. | |||
=== Expoentes Críticos === | |||
Para estudar mais sobre a eficiência dos algoritmos no modelo de Ising podemos definir a temperatura reduzida como: | |||
<math>t = \frac{T - T_c}{T_c}</math> | |||
Essa grandeza indica o quão distante estamos da temperatura crítica <math>T_c</math>, de modo que para <math>t=0</math> estamos em <math>T_c</math>. A partir disso, e sabendo que <math>\xi</math> indica a largura médio dos clusters, temos que a expressão <math>\xi \sim |t|^{- \nu}</math> demonstra a divergência da largura de correlação (largura dos clusters). Se tratando do tempo, definimos <math>\tau \sim |t|^{-z \nu}</math> como o tempo de correlação da simulação, medido em passos de Monte Carlo por sítio da rede. O expoente <math>z</math>, chamado de expoente dinâmico, é um modo de quantificar a diferença de tempo que acontece devido à divergência. Um valor grande de <math>z</math> simboliza que <math>\tau</math> fica grande, por exemplo, fazendo uma simulação mais demorada e menos precisa quando próximo de <math>T_c</math>. | |||
Combinando as duas equações vistas, podemos escrever que <math>\tau \sim \xi^z</math>. Essa relação indica que o tempo de correlação aumenta com o tamanho típico dos clusters. Considerando um sistema de tamanho finito porém (os tipos de sistema que simulamos), o valor máximo de <math>\xi</math> vai ser o tamanho <math>L</math> do sistema (e.g. um sistema <math>64</math>x<math>64</math> tem <math>L=64</math>). Podemos assim concluir que <math>\tau \sim L^z</math>. | |||
Sabendo a temperatura crítica do sistema (para Ising 2D, <math>T_c = 2.269J</math> é possível usar a relação <math>\tau \sim L^z</math> para medir <math>z</math> por meio de simulações onde a temperatura do sistema é igual à temperatura crítica para vários tamanhos diferentes de <math>L</math>, plotando <math>\tau</math> versus <math>L</math> em escala logarítmica. A inclinação da reta que liga todos esses pontos nos dá o valor de <math>z</math>. | |||
Por meio desse método, temos que o <math>z</math> do algoritmo de Metropolis é <math>z = 2.1655 \pm 0.0012</math> [5] e o <math>z</math> do algoritmo de Wolff (um algoritmo de clusterização) é <math>z = 0.25 \pm 0.001</math> [6]. | |||
O motivo do tempo grande do algoritmo de Metropolis é a divergência do tamanho de correlação <math>\xi</math> próximo da temperatura crítica. Ao se aproximar de <math>T_c</math>, grandes regiões se formam onde todos os spins estão alinhados, e é demorado para que o algoritmo inverta essas regiões, dado que ele inverte os spins sítio por sítio. | |||
Algoritmos de cluster, como o de Wolff, fazem uso da técnica de clusterização. Com isso, os algoritmos encontram agrupam spins alinhados em clusters que apontam para a mesma direção e invertem os spins desse cluster ao mesmo tempo. Algoritmos de clusterização permitem uma exploração mais efetivo do espaço de fase próximo da temperatura crítica por serem mais eficientes e de precisarem de menos iterações para terem medidas precisas. | |||
=== Balanço Detalhado === | === Balanço Detalhado === | ||
Para respeitarmos o Balanço Detalhado, precisamos que a mudança da rede de um estado $<math>\nu</math> para um estado <math>\mu</math> ocorra com a mesma probabilidade da mudança de um estado <math>\mu</math> para <math>\nu</math>, denotamos essa mudança por: <math>A(\mu \to \nu) = A(\nu \to \mu)</math>, com <math>A(x \to y)</math> sendo a razão de aceitação da mudança de um estado <math>x</math> para um estado <math>y</math>. | Para respeitarmos o Balanço Detalhado, precisamos que a mudança da rede de um estado $<math>\nu</math> para um estado <math>\mu</math> ocorra com a mesma probabilidade da mudança de um estado <math>\mu</math> para <math>\nu</math>, denotamos essa mudança por: <math>A(\mu \to \nu) = A(\nu \to \mu)</math>, com <math>A(x \to y)</math> sendo a razão de aceitação da mudança de um estado <math>x</math> para um estado <math>y</math>. | ||
| Linha 15: | Linha 47: | ||
\frac{(1-P_{add})^m A(\mu \to \nu)}{(1-P_{add})^n A(\nu \to \mu) } = e^{-\beta(E_{\nu} - E_{\mu})} = (1-P_{add})^{m-n}\frac{A(\mu \to \nu)}{A(\nu \to \mu)}</math>, tal que, | \frac{(1-P_{add})^m A(\mu \to \nu)}{(1-P_{add})^n A(\nu \to \mu) } = e^{-\beta(E_{\nu} - E_{\mu})} = (1-P_{add})^{m-n}\frac{A(\mu \to \nu)}{A(\nu \to \mu)}</math>, tal que, | ||
<math>\frac{A(\mu \to \nu)}{A(\nu \to \mu)} = \big[e^{2\beta J}(1-P_{add})\big]^{n-m}\;\;\;\; \Longrightarrow P_{add} = 1-e^{-2\beta J} \Longrightarrow \frac{(1-P_{add})^m A(\mu \to \nu)}{(1-P_{add})^n A(\nu \to \mu) }=1 </math> | <math>\frac{A(\mu \to \nu)}{A(\nu \to \mu)} = \big[e^{2\beta J}(1-P_{add})\big]^{n-m}\;\;\;\; \Longrightarrow P_{add} = 1-e^{-2\beta J} \Longrightarrow \frac{(1-P_{add})^m A(\mu \to \nu)}{(1-P_{add})^n A(\nu \to \mu) }=1 </math> | ||
== Algoritmo de Wolf == | == Algoritmo de Wolf == | ||
| Linha 32: | Linha 65: | ||
|- | |- | ||
|} | |} | ||
== Simulações == | == Simulações == | ||
| Linha 39: | Linha 71: | ||
!colspan="3"|Animações do algoritmo de Wolff em função da Temperatura <math>T</math>. | !colspan="3"|Animações do algoritmo de Wolff em função da Temperatura <math>T</math>. | ||
|- | |- | ||
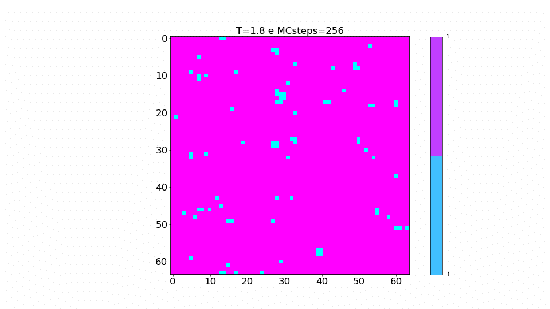
|[[Arquivo:TC-.gif|thumb|upright=4|none|alt=Alt text|Simulação para temperatura abaixo da temperatura crítica <math>T_c</math>.| | |[[Arquivo:TC-.gif|thumb|upright=4|none|alt=Alt text|Simulação para temperatura abaixo da temperatura crítica <math>T_c</math>.|550px]] | ||
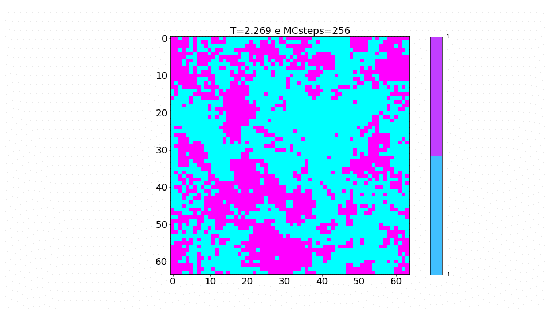
|[[Arquivo:hTC.gif|thumb|upright=4|none|alt=Alt text|Simulação na temperatura crítica <math>T_c</math>.| | |[[Arquivo:hTC.gif|thumb|upright=4|none|alt=Alt text|Simulação na temperatura crítica <math>T_c</math>.|550px]] | ||
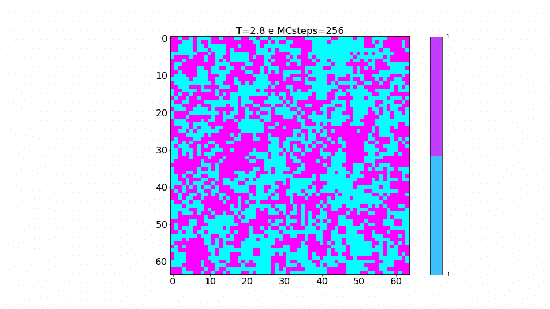
|[[Arquivo:TC+.gif|thumb|upright=4|none|alt=Alt text|Simulação para tempetura acima da temperatura | |[[Arquivo:TC+.gif|thumb|upright=4|none|alt=Alt text|Simulação para tempetura acima da temperatura crítica <math>T_c</math>.|550px]] | ||
|- | |- | ||
|} | |} | ||
== Propriedades do Algoritmo de Wolff == | |||
=== <math>P_{add}\;= \;1 - e^{-2\beta J} </math> === | |||
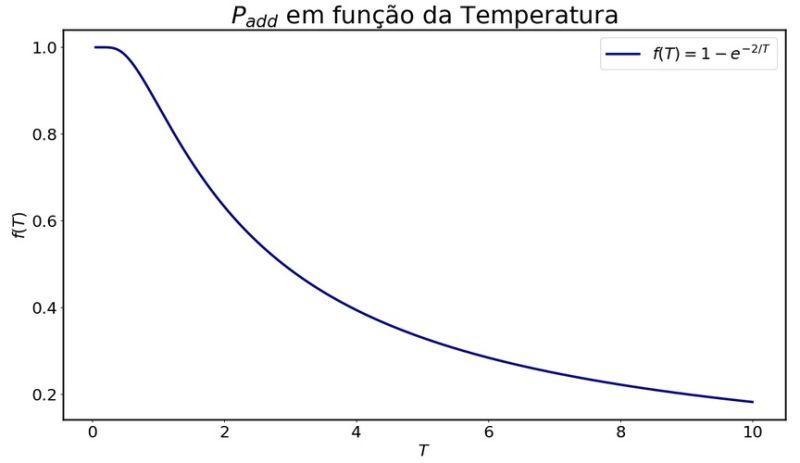
Nas animações acima, pode-se perceber que a temperatura tem papel importante na dinâmica apresentada em decorrência da forma com a qual está relacionada a probabilidade <math>P_{add}</math>, como podemos ver o gráfico a seguir: | |||
{| class="wikitable" style="text-align: center;" | |||
!colspan="1"|Probabilidade em função da temperatura. | |||
|- | |||
|[[Arquivo:Prob.jpeg|thumb|upright=4|none|alt=Alt text|Gráfico da probabilidade de aceitação <math>P_{add}</math> em função de <math>T</math>|800px]] | |||
|- | |||
|} | |||
Neste gráfico temos a probabilidade de um spin que possui a mesma orientação que o sítio inicial escolhido ser aceito e adicionado ao cluster em função da temperatura da rede. É de se esperar que conforme a temperatura aumente a probabilidade do spin ser adicionado ao cluster diminua e para temperaturas mais baixas espera-se o contrário. Com base nisso, podemos formular a ideia do tamanho médio dos cluster (<math>C_s</math>) que é invertido durante os passos de Monte Carlo em função da temperatura e associar este tamanho com a fração representada por este na rede. | |||
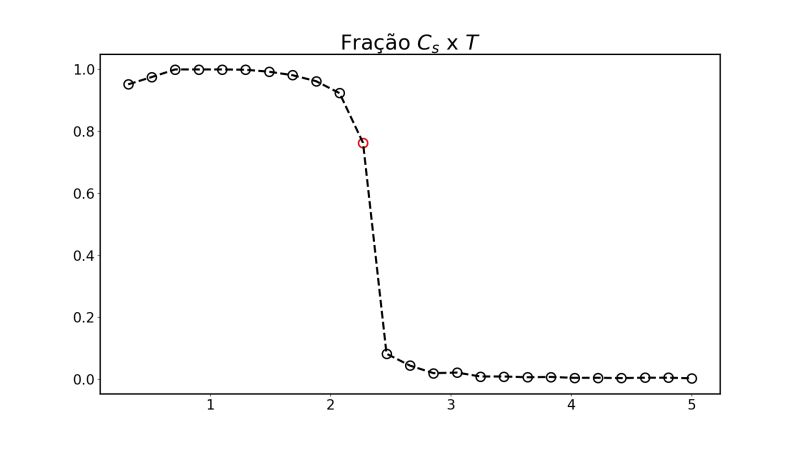
=== Fração do Tamanho dos Clusters (<math>C_s</math>) === | |||
No gráfico abaixo podemos perceber a mesma natureza que foi observados nas animações desenvolvidas, já que a fração do tamanho dos cluster diminui conforme a temperatura aumenta, ou seja, com a temperatura alta os clusters são menores e por isso representam uma fração menor e para temperatura acima de 3J essa fração é quase zero. Já para temperaturas mais baixas, essa fração aproxima-se de 1 o que significa que grande parte da rede, ou praticamente toda a rede, está sendo invertida em cada passo; exatamente o que observamos na animação para T=1.8J. | |||
{| class="wikitable" style="text-align: center;" | |||
!colspan="1"|Gráfico de <math>C_s</math>. | |||
|- | |||
|[[Arquivo:FCs.jpeg|thumb|upright=4|none|alt=Alt text|Gráfico de <math>C_s</math> em função de <math>T</math>|800px]] | |||
|- | |||
|} | |||
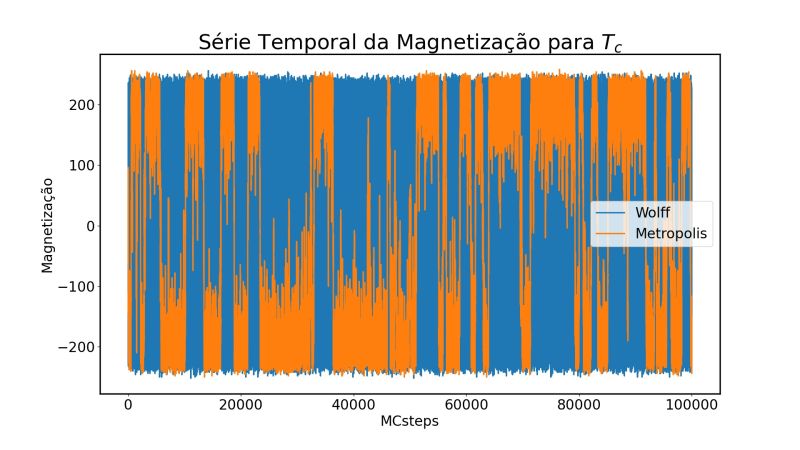
=== Série Temporal para a medida de magnetização === | |||
=== | |||
{| class="wikitable" style="text-align: center;" | {| class="wikitable" style="text-align: center;" | ||
!colspan="1"| | !colspan="1"|Série Temporal da magnetização. | ||
|- | |- | ||
|[[Arquivo: | |[[Arquivo:STmag.jpeg|thumb|upright=4|none|alt=Alt text|Gráfico da série temporal da medida de magnetização comparando os algoritmos|800px]] | ||
|- | |- | ||
|} | |} | ||
Podemos observar na figura acima medidas da magnetização usando o algoritmo de Wolff e o algoritmo de Metropolis para um sistema Ising 2D de mesmo tamanho (16x16) na temperatura crítica (<math>T_c=2.269J</math>). Nota-se que o algoritmo de Wolff explora o espaço de fase ao redor dessa temperatura em muito menos passos que o algoritmo de Metropolis, sendo mais eficiente para se obter medidas precisas ao redor dessa região. | |||
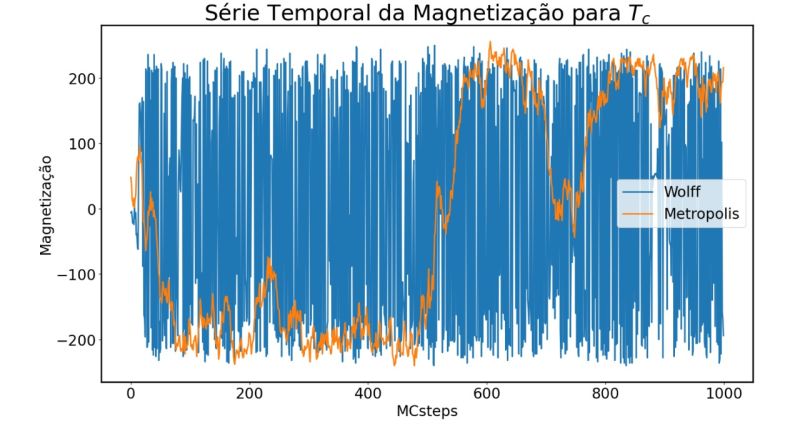
Na figura abaixo podemos observar esse mesmo sistema para um número menor de passos. É possível notar que para que o algoritmo de Metropolis inverta os clusters de spins alinhados a fim de chegar nos mesmos limites dos valores de magnetização há uma demora muito maior de tempo, que se deve à sua dinâmica de single spin flip. Nesse caso, enquanto Wolff já explora o espaço de fase ao redor de T_c em menos de 100 passos, Metropolis precisa de pelo menos 600 passos. | |||
Esse comportamento é o que esperamos dado a desaceleração crítica (critical slowing down), onde a medida que o sistema aumenta de tamanho se torna mais difícil de gerar configurações estatisticamente independentes [3]. Os clusters do algoritmo de Wolff mitigam esse efeito, sendo um sistema muito eficiente para eliminar correlações não locais. | |||
{| class="wikitable" style="text-align: center;" | |||
!colspan="1"|Série Temporal da magnetização até 1000 passos. | |||
|- | |||
|[[Arquivo:STmagShort.jpeg|thumb|upright=4|none|alt=Alt text|Gráfico da série temporal da medida de magnetização comparando os algoritmos nos primeiros 1000 passos|800px]] | |||
|- | |||
|} | |||
== Códigos Fonte == | == Códigos Fonte == | ||
| Linha 80: | Linha 138: | ||
rfloat1 = rng.random() | rfloat1 = rng.random() | ||
if (rfloat1<prob) : #IF da inclusão no cluster | if (rfloat1<prob) : #IF da inclusão no cluster | ||
stack.append(nn) | stack.append(nn) | ||
sp = sp+1 | sp = sp+1 | ||
| Linha 86: | Linha 143: | ||
return | return | ||
</source> | </source> | ||
=== Função do Cálculo da Magnetização === | |||
<source lang=Py> | |||
def cluster_din_mag(sitio, mag): | |||
stack = [] | |||
oldspin = s[sitio] | |||
newspin = (-1)*s[sitio] | |||
s[sitio] = newspin | |||
mag = mag +2*s[sitio] | |||
sp=1 | |||
stack.append(sitio) | |||
while (sp): | |||
sp = sp-1 | |||
atual = stack[sp] | |||
stack.pop() | |||
for j in range(4): | |||
nn=viz[atual][j] | |||
if s[nn] == oldspin: | |||
rfloat1 = rng.random() | |||
if (rfloat1<prob) : #IF da inclusão no buffer | |||
stack.append(nn) | |||
sp = sp+1 | |||
s[nn] = newspin | |||
mag = mag +2*s[nn] | |||
return mag | |||
</source> | |||
== Conclusão == | |||
Conclui-se então que os resultados obtidos com o códigos produzidos estão, de certa forma, de acordo com o esperado e fez-se possível elucidar as diferenças entre as duas dinâmicas dos algoritmos (Metropolis e Wolff) mostrando os pontos positivos do algoritmo de Wolff e as razões pelas quais se sai melhor na geração de dados estatisticamente independentes do modelo de Ising 2D. Todos os códigos, imagens e gifs gerados para esta apresentação estão disponíveis em: https://github.com/mgteus/MonteCarlo. | |||
== Referências == | == Referências == | ||
[1] M. E. J. Newman, G. T. Barkema, "Monte Carlo Methods in Statistical Physics". Oxford University Press Inc., New York, 1999. | |||
[2] Materias da disciplina disponíveis em: <https://moodle.ufrgs.br/course/view.php?id=80767> | |||
[3] E. Luijten, “Introduction to Cluster Monte Carlo Algorithms” <http://csml.northwestern.edu/resources/Reprints/lnp_color.pdf> | |||
[4] <https://fiscomp.if.ufrgs.br/index.php/Ising_2D> | |||
[5] Nightingale and Blöte (1996). | |||
[6] Coddington e Baillie (1992). | |||
Edição atual tal como às 17h32min de 13 de outubro de 2021
PÁGINA EM CONSTRUÇÃO
Clusterização do Modelo de Ising
O modelo de Ising é definido como uma malha de tamanho L, quadrada quando em duas dimensões e cúbica quando em três dimensões, onde cada vértice apresenta um componente de spin de magnitude fixa que pode apontar para cima ou para baixo (+1 ou -1, respectivamente). O sistema pode ser descrito pelo seguinte hamiltoniano:
onde representa o valor do spin e a soma é feita sobre os pares de vértices próximas que são conectadas com um acoplamento ferromagnético de força .
Para um modelo de Ising bidimensional (o tipo que consideramos) é possível calcular [1] sua temperatura crítica exata como:
Acima dessa temperatura o sistema está na ‘’’fase paramagnética‘’’, onde a magnetização média é nula, e abaixo dessa temperatura o sistema está na fase ‘’’fase ferromagnética’’’, onde a maioria dos spins se alinham e a magnetização se torna não-nula. Ao estudar o modelo de Ising em geral temos maior interesse no comportamento do sistema perto de , onde o sistema forma grupos grandes de spins para cima ou para baixo. Esses grupos contribuem muito para a energia do sistema, causando muita flutuação quando invertem.
O algoritmo de Metropolis é um ótimo algoritmo para realizar simulações do modelo de Ising [1]. Porém, sua dinâmica de flip único é ineficiente especialmente quando próxima da temperatura crítica do sistema. As imprecisões estatísticas de quantidades como magnetização e energia interna do sistema aumentam quando próximo da temperatura crítica. Assim, quando esses grandes grupos de spins alinhados (clusters) invertem, há grandes imprecisões. Essa imprecisão aumenta com o tamanho das flutuações, mas diminui com o número de medidas feitas na simulação, então para se estudar a região perto de de modo mais preciso é necessário que a simulação aconteça por mais tempo. Porém, uma outra fraqueza do algoritmo de Metropolis é seu tempo de correlação grande ao redor da temperatura crítica. Isso significa que o número de medidas de uma simulação é pequena, então para diminuir as imprecisões estatísticas causadas pelas poucas medidas é necessário rodar o algoritmo por mais tempo.
Uma das propriedades do modelo de Ising é o fato de flutuações grandes gerarem medidas mais imprecisas. Porém, o tempo de correlação e o modo como ele se comporta próximo a é uma propriedade do algoritmo utilizado para estudar o sistema, e então é algo que pode ser otimizado.
Expoentes Críticos
Para estudar mais sobre a eficiência dos algoritmos no modelo de Ising podemos definir a temperatura reduzida como:
Essa grandeza indica o quão distante estamos da temperatura crítica , de modo que para estamos em . A partir disso, e sabendo que indica a largura médio dos clusters, temos que a expressão demonstra a divergência da largura de correlação (largura dos clusters). Se tratando do tempo, definimos como o tempo de correlação da simulação, medido em passos de Monte Carlo por sítio da rede. O expoente , chamado de expoente dinâmico, é um modo de quantificar a diferença de tempo que acontece devido à divergência. Um valor grande de simboliza que fica grande, por exemplo, fazendo uma simulação mais demorada e menos precisa quando próximo de .
Combinando as duas equações vistas, podemos escrever que . Essa relação indica que o tempo de correlação aumenta com o tamanho típico dos clusters. Considerando um sistema de tamanho finito porém (os tipos de sistema que simulamos), o valor máximo de vai ser o tamanho do sistema (e.g. um sistema x tem ). Podemos assim concluir que .
Sabendo a temperatura crítica do sistema (para Ising 2D, é possível usar a relação para medir por meio de simulações onde a temperatura do sistema é igual à temperatura crítica para vários tamanhos diferentes de , plotando versus em escala logarítmica. A inclinação da reta que liga todos esses pontos nos dá o valor de .
Por meio desse método, temos que o do algoritmo de Metropolis é [5] e o do algoritmo de Wolff (um algoritmo de clusterização) é [6].
O motivo do tempo grande do algoritmo de Metropolis é a divergência do tamanho de correlação próximo da temperatura crítica. Ao se aproximar de , grandes regiões se formam onde todos os spins estão alinhados, e é demorado para que o algoritmo inverta essas regiões, dado que ele inverte os spins sítio por sítio.
Algoritmos de cluster, como o de Wolff, fazem uso da técnica de clusterização. Com isso, os algoritmos encontram agrupam spins alinhados em clusters que apontam para a mesma direção e invertem os spins desse cluster ao mesmo tempo. Algoritmos de clusterização permitem uma exploração mais efetivo do espaço de fase próximo da temperatura crítica por serem mais eficientes e de precisarem de menos iterações para terem medidas precisas.
Balanço Detalhado
Para respeitarmos o Balanço Detalhado, precisamos que a mudança da rede de um estado $ para um estado ocorra com a mesma probabilidade da mudança de um estado para , denotamos essa mudança por: , com sendo a razão de aceitação da mudança de um estado para um estado .
Supondo que estamos mudando de um estado para outro estado , temos que a diferença de energia entre esses dois é resultado da quebra das ligações entre pares de spins orientados na mesma direção que não foram adicionados ao cluster, já que, não há uma garantia que a ida de quebre a mesma quantidade de ligações que a volta de . A probabilidade de não adicionarmos um spin vizinho ao cluster é dada por: ; uma vez que é a probabilidade de incluir esse spin no cluster.
Supondo que existam ligações a serem quebradas na ida de , a probabilidade desse evento é dada por . Porém, o mesmo pode não valer para a volta de , em razão disso, precisamos analisar o caso em que não há o mesmo número de ligações a serem quebradas na volta e então a probabilidade será dada por com sendo o número de ligações a serem quebradas de .
Consideramos agora que e sejam as energias associadas aos estados e , respectivamente, temos que: a cada ligações que são quebradas de a energia aumenta com e para cada novas ligações geradas de a energia diminui com . Pode-se escrever então que a diferença de energia entre e é dada por:
Seguindo a definição do Balanço Detalhado e impondo que o Processo Markoviano dessas mudanças de estados descritas acima respeite a Distribuição de Boltzmann, precisamos que: , tal que,
Algoritmo de Wolf
Dinâmica do Algoritmo
O algoritmo de Wolff baseia-se principalmente em 4 passos. são estes:
- 1 - Escolhe-se um sítio aleatório da rede;
- 2 - Entre seus 4 vizinhos, se o spin do vizinho for igual ao do sítio inicial, adicionamos o vizinho ao cluster com probabilidade
- 3 - Para cada vizinho que foi adicionado ao cluster no passo anterior, repetimos o processo do passo 2 adicionando os vizinhos desse vizinho que possuem spin na mesma direção com a mesma probabilidade . Faz-se isso para todos os sítios que são adicionados ao cluster.
- 4 - Quando todos os vizinhos de todos os sítios adicionados ao cluster tiveram ao menos uma “chance” de serem adicionados ao cluster, flipamos o cluster.
| Dinâmica do algoritmo. | |
|---|---|
Simulações
Animações
| Animações do algoritmo de Wolff em função da Temperatura . | ||
|---|---|---|
Propriedades do Algoritmo de Wolff
Nas animações acima, pode-se perceber que a temperatura tem papel importante na dinâmica apresentada em decorrência da forma com a qual está relacionada a probabilidade , como podemos ver o gráfico a seguir:
| Probabilidade em função da temperatura. |
|---|
Neste gráfico temos a probabilidade de um spin que possui a mesma orientação que o sítio inicial escolhido ser aceito e adicionado ao cluster em função da temperatura da rede. É de se esperar que conforme a temperatura aumente a probabilidade do spin ser adicionado ao cluster diminua e para temperaturas mais baixas espera-se o contrário. Com base nisso, podemos formular a ideia do tamanho médio dos cluster () que é invertido durante os passos de Monte Carlo em função da temperatura e associar este tamanho com a fração representada por este na rede.
Fração do Tamanho dos Clusters ()
No gráfico abaixo podemos perceber a mesma natureza que foi observados nas animações desenvolvidas, já que a fração do tamanho dos cluster diminui conforme a temperatura aumenta, ou seja, com a temperatura alta os clusters são menores e por isso representam uma fração menor e para temperatura acima de 3J essa fração é quase zero. Já para temperaturas mais baixas, essa fração aproxima-se de 1 o que significa que grande parte da rede, ou praticamente toda a rede, está sendo invertida em cada passo; exatamente o que observamos na animação para T=1.8J.
| Gráfico de . |
|---|
Série Temporal para a medida de magnetização
| Série Temporal da magnetização. |
|---|
Podemos observar na figura acima medidas da magnetização usando o algoritmo de Wolff e o algoritmo de Metropolis para um sistema Ising 2D de mesmo tamanho (16x16) na temperatura crítica (). Nota-se que o algoritmo de Wolff explora o espaço de fase ao redor dessa temperatura em muito menos passos que o algoritmo de Metropolis, sendo mais eficiente para se obter medidas precisas ao redor dessa região.
Na figura abaixo podemos observar esse mesmo sistema para um número menor de passos. É possível notar que para que o algoritmo de Metropolis inverta os clusters de spins alinhados a fim de chegar nos mesmos limites dos valores de magnetização há uma demora muito maior de tempo, que se deve à sua dinâmica de single spin flip. Nesse caso, enquanto Wolff já explora o espaço de fase ao redor de T_c em menos de 100 passos, Metropolis precisa de pelo menos 600 passos.
Esse comportamento é o que esperamos dado a desaceleração crítica (critical slowing down), onde a medida que o sistema aumenta de tamanho se torna mais difícil de gerar configurações estatisticamente independentes [3]. Os clusters do algoritmo de Wolff mitigam esse efeito, sendo um sistema muito eficiente para eliminar correlações não locais.
| Série Temporal da magnetização até 1000 passos. |
|---|
Códigos Fonte
Função da Dinâmica de Clusterização
def cluster_din(sitio):
stack = []
oldspin = s[sitio]
newspin = (-1)*s[sitio]
s[sitio] = newspin
sp=1
stack.append(sitio)
while (sp):
sp = sp-1
atual = stack[sp]
stack.pop()
for j in range(4):
nn=viz[atual][j]
if s[nn] == oldspin: #IF da orientação do vizinho
rfloat1 = rng.random()
if (rfloat1<prob) : #IF da inclusão no cluster
stack.append(nn)
sp = sp+1
s[nn] = newspin
return
Função do Cálculo da Magnetização
def cluster_din_mag(sitio, mag):
stack = []
oldspin = s[sitio]
newspin = (-1)*s[sitio]
s[sitio] = newspin
mag = mag +2*s[sitio]
sp=1
stack.append(sitio)
while (sp):
sp = sp-1
atual = stack[sp]
stack.pop()
for j in range(4):
nn=viz[atual][j]
if s[nn] == oldspin:
rfloat1 = rng.random()
if (rfloat1<prob) : #IF da inclusão no buffer
stack.append(nn)
sp = sp+1
s[nn] = newspin
mag = mag +2*s[nn]
return mag
Conclusão
Conclui-se então que os resultados obtidos com o códigos produzidos estão, de certa forma, de acordo com o esperado e fez-se possível elucidar as diferenças entre as duas dinâmicas dos algoritmos (Metropolis e Wolff) mostrando os pontos positivos do algoritmo de Wolff e as razões pelas quais se sai melhor na geração de dados estatisticamente independentes do modelo de Ising 2D. Todos os códigos, imagens e gifs gerados para esta apresentação estão disponíveis em: https://github.com/mgteus/MonteCarlo.
Referências
[1] M. E. J. Newman, G. T. Barkema, "Monte Carlo Methods in Statistical Physics". Oxford University Press Inc., New York, 1999.
[2] Materias da disciplina disponíveis em: <https://moodle.ufrgs.br/course/view.php?id=80767>
[3] E. Luijten, “Introduction to Cluster Monte Carlo Algorithms” <http://csml.northwestern.edu/resources/Reprints/lnp_color.pdf>
[4] <https://fiscomp.if.ufrgs.br/index.php/Ising_2D>
[5] Nightingale and Blöte (1996).
[6] Coddington e Baillie (1992).








































![{\displaystyle {\frac {A(\mu \to \nu )}{A(\nu \to \mu )}}={\big [}e^{2\beta J}(1-P_{add}){\big ]}^{n-m}\;\;\;\;\Longrightarrow P_{add}=1-e^{-2\beta J}\Longrightarrow {\frac {(1-P_{add})^{m}A(\mu \to \nu )}{(1-P_{add})^{n}A(\nu \to \mu )}}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dc7dd4e75a96a1458cc3ccebcb3c98a06bc3d7e)