Termostato de Nosé-Hoover: mudanças entre as edições
Sem resumo de edição |
|||
| (11 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
== Termostato de Nosé-Hoover == | == Termostato de Nosé-Hoover == | ||
O termostato de Nosé-Hoover é um algoritmo utilizado para simulação de dinâmica molecular. Esse ensemble é relevante quando o sistema em estudo está em contato com um banho térmico, para manter a temperatura constante<ref name=ensemble_nvt> https://www2.ph.ed.ac.uk/~dmarendu/MVP/MVP03.pdf </ref>. A maneira que o algoritmo de Nosé-Hoover mantém a temperatura constante é a partir da adição de uma variável dinâmica fictícia (um "agente" externo), que atua sobre as velocidades das partículas no sistema, as acelerando ou desacelerando até que estas atinjam a temperatura desejada. | O termostato de Nosé-Hoover é um algoritmo utilizado para simulação de dinâmica molecular. Esse ensemble é relevante quando o sistema em estudo está em contato com um banho térmico, para manter a temperatura constante e obter uma amostragem de acordo com a distribuição canônica<ref name=ensemble_nvt> https://www2.ph.ed.ac.uk/~dmarendu/MVP/MVP03.pdf </ref>. A maneira que o algoritmo de Nosé-Hoover mantém a temperatura constante é a partir da adição de uma variável dinâmica fictícia (um "agente" externo), que atua sobre as velocidades das partículas no sistema, as acelerando ou desacelerando até que estas atinjam a temperatura desejada. | ||
Este trabalho tem como objetivo simular um fluído de Lennard Jones a partir do termostato de Nosé-Hoover, a fim de estudar o efeito das variáveis presentes no modelo do termostato sobre as variáveis física do sistema. | Este trabalho tem como objetivo simular um fluído de Lennard Jones a partir do termostato de Nosé-Hoover, a fim de estudar o efeito das variáveis presentes no modelo do termostato sobre as variáveis física do sistema. | ||
| Linha 10: | Linha 7: | ||
== Método == | == Método == | ||
=== Termostato de | === Termostato de Nosé === | ||
Para entender o termostado de Nóse-Hoover, primeiramente será mostrado o termostato de Nosé<ref name=nose> NOSÉ, Shuichi, '''A molecular dynamics method for simulations in the canonical ensemble''', Molecular Physics, 1984, Vol. 52, No. 2, 255-268 </ref>. | Para entender o termostado de Nóse-Hoover, primeiramente será mostrado o termostato de Nosé<ref name=nose> NOSÉ, Shuichi, '''A molecular dynamics method for simulations in the canonical ensemble''', Molecular Physics, 1984, Vol. 52, No. 2, 255-268 </ref>. | ||
| Linha 16: | Linha 13: | ||
Este termostato atribui coordenadas generalizados adicionais <math> s </math> e o seu momento conjugado <math> p_s </math> ao banho térmico. O fator <math> s </math> é definido como um fator de escala das velocidades, onde: | Este termostato atribui coordenadas generalizados adicionais <math> s </math> e o seu momento conjugado <math> p_s </math> ao banho térmico. O fator <math> s </math> é definido como um fator de escala das velocidades, onde: | ||
<math> | <math> \bold v = s\dot \bold r = s\bold p/m</math> | ||
E também são definidas as energia potenciais e cinética associadas a <math> s </math> como: | E também são definidas as energia potenciais e cinética associadas a <math> s </math> como: | ||
<math> \mathcal U_s = (N_f + 1) | <math> \mathcal U_s = (N_f + 1)k_BT \ln(s) </math> | ||
e | e | ||
<math> \mathcal K_s = \frac{1}{2}Q\dot s^2 = \frac{p_s^2}{2Q} </math> | <math> \mathcal K_s = \frac{1}{2}Q\dot s^2 = \frac{p_s^2}{2Q} </math> | ||
| Linha 28: | Linha 27: | ||
O Lagrangiano do sistema extendida (consistente das partículas e do banho térmico) então é postulado como: | O Lagrangiano do sistema extendida (consistente das partículas e do banho térmico) então é postulado como: | ||
<math> \mathcal L = \mathcal K + \mathcal K_s - \mathcal U - \mathcal U_s = \sum_i \frac{\bold p_i^2}{2m_is^2} + \frac{p_s^2}{2Q} - \mathcal U(\bold r) - (N_f + 1)k_BTln(s)</math> | <math> \mathcal L = \mathcal K + \mathcal K_s - \mathcal U - \mathcal U_s = \sum_i \frac{\bold p_i^2}{2m_is^2} + \frac{p_s^2}{2Q} - \mathcal U(\bold r) - (N_f + 1)k_BTln(s)</math>. | ||
Como não é explicitamente dependente do tempo: | Como não é explicitamente dependente do tempo: | ||
<math> \mathcal H_N = \mathcal K + \mathcal K_s + \mathcal U + \mathcal U_s = \sum_i \frac{\bold p_i^2}{2m_is^2} + \frac{p_s^2}{2Q} + \mathcal U(\bold r) + (N_f + 1)k_BTln(s)</math> | <math> \mathcal H_N = \mathcal K + \mathcal K_s + \mathcal U + \mathcal U_s = \sum_i \frac{\bold p_i^2}{2m_is^2} + \frac{p_s^2}{2Q} + \mathcal U(\bold r) + (N_f + 1)k_BTln(s)</math>. | ||
<math> \mathcal H_N </math> se conserva. <ref name=L5> http://www.courses.physics.helsinki.fi/fys/moldyn/lectures/L5.pdf </ref>. | |||
Assim, as equações de movimento podem ser deduzidas: | Assim, as equações de movimento podem ser deduzidas: | ||
<math> \bold \dot r_i = \frac{\partial \mathcal H_N}{\partial \bold p_i} = \bold p_i | <math> \bold \dot r_i = \frac{\partial \mathcal H_N}{\partial \bold p_i} = \frac{\bold p_i}{m_is^2}</math> | ||
<math> \bold \dot p = -\frac{\partial \mathcal H_N}{\partial \bold r_i} = \bold f_i</math> | <math> \bold \dot p = -\frac{\partial \mathcal H_N}{\partial \bold r_i} = \bold f_i</math> | ||
<math> \dot s = \frac{\partial \mathcal H_N}{\partial p_s} = p_s/Q</math> | <math> \dot s = \frac{\partial \mathcal H_N}{\partial p_s} = p_s/Q</math> | ||
| Linha 47: | Linha 45: | ||
<math> \dot p_s = -\frac{\partial \mathcal H_N}{\partial s} = \sum_i \frac{\bold p_i^2}{m_is^3} - (N_f + 1)k_BT/s </math> | <math> \dot p_s = -\frac{\partial \mathcal H_N}{\partial s} = \sum_i \frac{\bold p_i^2}{m_is^3} - (N_f + 1)k_BT/s </math> | ||
Assim, para tempos longos, o termostato de | Assim, para tempos longos, o termostato de Nosé pode ser tratado como um sistema de partículas junto a um banho térmico, ou seja, como um ensemble canônico. Entretanto, o valor de <math> Q </math> precisa ser determinado por tentativa e erro. Outro problema do termostato de Nosé é o fato de que, por as velocidades serem escaladas com o <math> s </math>, o tempo também será escalado com <math> s </math>, o que não acontece em sistemas reais e extendidos. <ref name=L5></ref> | ||
=== Termostato de Nosé-Hoover === | === Termostato de Nosé-Hoover === | ||
| Linha 57: | Linha 55: | ||
<math> \bold \dot p = \bold f_i - \xi \bold p_i = \bold f_i \frac{p_\eta}{Q}\bold p_i </math> | <math> \bold \dot p = \bold f_i - \xi \bold p_i = \bold f_i \frac{p_\eta}{Q}\bold p_i </math> | ||
<math> \dot \eta = \ | <math> \dot \eta = p_\eta/Q </math> | ||
<math> \dot p_\eta = \sum_i \frac{\bold p_i^2}{m_i} - N_fk_BT </math> | |||
onde <math> \eta </math> agora | onde <math> \eta </math> agora são os termos relacionados à fricção do banho térmico. | ||
=== Cadeias de | === Cadeias de Nosé-Hoover === | ||
O termostato de Nosé-Hoover gera distribuição canônica quando não | O termostato de Nosé-Hoover gera distribuição canônica quando não há forças externas ao sistema. Enquanto existem sistemas com forças externas que podem apresentar este comportamento, existem casos com forças externas onde esse termostato não gera o comportamento esperado. Para contornar esse problema, Martyna et al. <ref name=chains> MARTYNA, G. J., KLEIN, M. L., TUCKERMAN, M. '''Nosé-Hoover chains: The canonical ensemble via continuous dynamics''' J. Chem. Phys. 1992, Vol. 97 No. 4. </ref> propuseram uma solução onde um termostato de Nosé-Hoover está acoplado a outro termostato de Nosé-Hover, formando uma cadeia. Este sistema ainda irá gerar uma distribuição canônica e não apresentará problemas com forças externas. As equações de movimento para um sistema com M termostatos são: | ||
<math> \bold \dot r_i = \frac{\bold p_i}{m_i} </math> | <math> \bold \dot r_i = \frac{\bold p_i}{m_i} </math> | ||
| Linha 71: | Linha 71: | ||
<math> \dot \xi_k = \frac{p_{\xi,k}}{q_k} \quad k=1,...,M </math> | <math> \dot \xi_k = \frac{p_{\xi,k}}{q_k} \quad k=1,...,M </math> | ||
<math> \dot p_{\xi, 1} = \left(\sum_i\frac{p_i^2}{m_i} - Lk_BT\right) - \frac{p_{\xi,2}}{ | <math> \dot p_{\xi, 1} = \left(\sum_i\frac{p_i^2}{m_i} - Lk_BT\right) - \frac{p_{\xi,2}}{Q_2}p_{\xi,1} </math> | ||
<math> \dot p_{\xi, k} = \left[\frac{p_{\xi_{k-1}}^2}{Q_{k-1}} - k_BT\right] - \frac{p_{\xi_{k+1}}}{Q_{k+1}} </math> | <math> \dot p_{\xi, k} = \left[\frac{p_{\xi_{k-1}}^2}{Q_{k-1}} - k_BT\right] - \frac{p_{\xi_{k+1}}}{Q_{k+1}} </math> | ||
| Linha 85: | Linha 85: | ||
Utilizando o termostato de Nosé-Hoover, serão feitos gráficos utilizando diferentes valores de <math> Q </math>, a fim de analisar qual é o efeito dessa variável sobre o sistema. Para melhor análise, primeiramente o sistema será estabilizado com a temperatura <math> T = 1.0 </math>, e então terá um '''pulo''' na temperatura para <math> T = 1.5 </math>, com isso será possível analisar qual é o efeito da inércia térmica do banho térmico do sistema. | Utilizando o termostato de Nosé-Hoover, serão feitos gráficos utilizando diferentes valores de <math> Q </math>, a fim de analisar qual é o efeito dessa variável sobre o sistema. Para melhor análise, primeiramente o sistema será estabilizado com a temperatura <math> T = 1.0 </math>, e então terá um '''pulo''' na temperatura para <math> T = 1.5 </math>, com isso será possível analisar qual é o efeito da inércia térmica do banho térmico do sistema. | ||
Serão feitos gráficos da temperatura ao longo do tempo de simulação, onde será possível observar as flutuações que ocorrem no sistema, além de um gráfico para mostrar a depedência da velocidade das partículas de acordo com o <math> Q </math> escolhido. | Serão feitos gráficos da temperatura ao longo do tempo de simulação, onde será possível observar as flutuações que ocorrem no sistema, além de um gráfico para mostrar a depedência da velocidade das partículas de acordo com o <math> Q </math> escolhido. Este trabalho é baseado no Case Study 11 do livro "Understanding Molecular Simulation" - Daan Frenkel e Berend Smit: "Lennard-Jones: Nosé-Hoover Termostat" | ||
== Resultados == | == Resultados == | ||
Primeiramente, foi feita uma simulação, com <math> T = 1.0 </math> constante ao longo de toda simulação, conforme visto | === Temperatura constante === | ||
Primeiramente, foi feita uma simulação, com <math> T = 1.0 </math> constante ao longo de toda simulação utilizando três diferentes valores para a inércia do banho térmico, <math> Q = 0.1 </math> (que será chamado de "<math> Q </math> baixo"), <math> Q = 1.0 </math> ("<math> Q </math> intermediário") e <math> Q = 10.0 </math> ("<math> Q </math> alto"), conforme visto nas figuras 1, 2 e 3. É notável que existem intensas oscilações na temperatura no início da simulação para cada <math> Q </math> utilizado, devido ao tempo que o sistema leva para atingir o equilíbrio. Além disso, as oscilações se mantém ao longo de toda simulação. | |||
[[Arquivo:NH Q01 cte.jpeg|800px|center|thumb|Figura 1: Evolução da temperatura durante a simulação com <math> Q = 0.1 </math>.]] | |||
[[Arquivo:NH Q1 cte.jpeg|800px|center|thumb|Figura 2: Evolução da temperatura durante a simulação com <math> Q = 0.1 </math>.]] | |||
[[Arquivo:NH | [[Arquivo:NH Q10 cte.jpeg|800px|center|thumb|Figura 3: Evolução da temperatura durante a simulação com <math> Q = 0.1 </math>.]] | ||
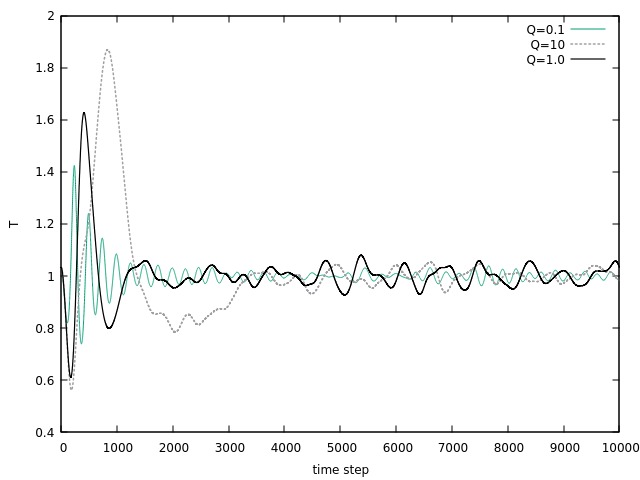
Na figura 4 vemos, diretamente, a diferença causada pelos diferentes valores de <math> Q </math>. Para um <math> Q </math> baixo, existem oscilações pouco intensas mas de maior frequência, para um <math> Q </math> alto o sistema tende para a temperatura desejada sem muitas oscilações. O comportamento do <math> Q </math> intermediário se encontra entre os dois valores de <math> Q </math> testados. | |||
[[Arquivo:NH | [[Arquivo:NH T cte.jpeg|800px|center|thumb|Figura 4: Evolução da temperatura durante a simulação.]] | ||
=== Salto de temperatura === | |||
[[Arquivo:NH 3Q.jpeg]] | Abaixo são demonstradas situações onde houve um salto da temperatura de <math> T = 1.0 </math> para <math> T = 1.5 </math> a partir do passo <math> 12000 </math> (esse valor foi escolhido para ter certeza que o sistema já se encontrava no equílibrio neste instante), utilizando os mesmos três diferentes valores da variável referente a inércia do banho térmico do exemplo acima. | ||
[[Arquivo:NH Q01.jpeg|800px|center|thumb|Figura 5: Evolução da temperatura para um sistema com <math> Q = 0.1 </math> com salto para <math> T = 1.5 </math>]] | |||
[[Arquivo:NH Q1.jpeg|800px|center|thumb|Figura 6: Evolução da temperatura para um sistema com <math> Q = 1.0 </math> com salto para <math> T = 1.5 </math>]] | |||
[[Arquivo:NH Q10.jpeg|800px|center|thumb|Figura 7: Evolução da temperatura para um sistema com <math> Q = 10.0 </math> com salto para <math> T = 1.5 </math>]] | |||
O que nota-se neste resultado, e que fica mais claro na figura 8, é que para um valor de <math> Q </math> baixo, ou seja, baixa inércia térmica, a temperatura do sistema possui muitas oscilações quando acontece o pulo, logo o sistema demora mais para se estabilizar, entretanto, quando estabilizado as oscilações são menores do que para valores de <math> Q </math> maiores. Para um <math> Q </math> alto, a temperatura não oscila depois do pulo, tendendo rapidamente para o valor desejado, entretanto, possuindo oscilações maiores do que para um <math> Q </math> baixo. O resultado de <math> Q </math> intermediário apresenta um comportamento entre os outros dois resultados, apresentando oscilações após o pulo, mas rapidamente tendendo para o valor desejado. | |||
[[Arquivo:NH 3Q.jpeg|800px|center|thumb|Figura 8: Evolução da temperatura para um sistema com salto para <math> T = 1.5 </math>]] | |||
Conforme visto, o valor de <math> Q </math> influência o equilíbrio do sistema, portanto, conforme dito anteriormente, este valor precisa ser determinado, para cada sistema, por tentativa e erro. | Conforme visto, o valor de <math> Q </math> influência o equilíbrio do sistema, portanto, conforme dito anteriormente, este valor precisa ser determinado, para cada sistema, por tentativa e erro. | ||
| Linha 107: | Linha 121: | ||
Entretanto, o valor de <math> Q </math> não pode afetar as propriedades físicas da partícula, como a velocidade. Visto que a velocidade da partícula, ou seja, a temperatura média do sistema, é independente de <math> Q </math>, um gráfico da distribuição de Maxwell-Boltzmann para cada situação tem de ser idêntico à todos outros valores de <math> Q </math>. Isso é demonstrado nas figuras abaixo. | Entretanto, o valor de <math> Q </math> não pode afetar as propriedades físicas da partícula, como a velocidade. Visto que a velocidade da partícula, ou seja, a temperatura média do sistema, é independente de <math> Q </math>, um gráfico da distribuição de Maxwell-Boltzmann para cada situação tem de ser idêntico à todos outros valores de <math> Q </math>. Isso é demonstrado nas figuras abaixo. | ||
[[Arquivo:NH V Q01.jpeg|800px|center|thumb|Figura 8: Velocidade das partículas e distribuição de Maxwell-Boltzmann utilizando <math> Q = 0.1 </math>.]] | |||
[[Arquivo:NH V Q1.jpeg|800px|center|thumb|Figura 8: Velocidade das partículas e distribuição de Maxwell-Boltzmann utilizando <math> Q = 1.0 </math>.]] | |||
[[Arquivo:NH V 2Qs.jpeg|800px|center|thumb|Figura 8: Velocidade das partículas e distribuição de Maxwell-Boltzmann.]] | |||
== Conclusões e Perspectivas Futuras == | |||
Com o trabalho apresentado, foi possível utilizar o termostato de Nosé-Hoover para fazer análise do sistema proposto. Entrentanto ainda é necessário expandir este trabalho além de melhorias que poderiam ser feitas, como o cálculo do deslocamento quadrado médio das partículas no banho térmico. | |||
== Programas Utilizados == | == Programas Utilizados == | ||
| Linha 119: | Linha 139: | ||
/*********************************************/ | /*********************************************/ | ||
// Simulação de DM de um fluido de Lennard-Jones com termostato | // Simulação de DM de um fluido de Lennard-Jones com termostato Nosé-Hoover Compile usando "gcc -o NVT_NH NVT_NH.c -lm -lgsl" // | ||
/********************************************/ | /********************************************/ | ||
| Linha 434: | Linha 454: | ||
/*********************************************/ | /*********************************************/ | ||
// Simulação de DM de um fluido de Lennard-Jones com termostato | // Simulação de DM de um fluido de Lennard-Jones com termostato Nosé-Hoover Compile usando "gcc -o NVT_NH NVT_NH.c -lm -lgsl" // | ||
/********************************************/ | /********************************************/ | ||
Edição atual tal como às 14h12min de 4 de julho de 2021
Termostato de Nosé-Hoover
O termostato de Nosé-Hoover é um algoritmo utilizado para simulação de dinâmica molecular. Esse ensemble é relevante quando o sistema em estudo está em contato com um banho térmico, para manter a temperatura constante e obter uma amostragem de acordo com a distribuição canônica[1]. A maneira que o algoritmo de Nosé-Hoover mantém a temperatura constante é a partir da adição de uma variável dinâmica fictícia (um "agente" externo), que atua sobre as velocidades das partículas no sistema, as acelerando ou desacelerando até que estas atinjam a temperatura desejada.
Este trabalho tem como objetivo simular um fluído de Lennard Jones a partir do termostato de Nosé-Hoover, a fim de estudar o efeito das variáveis presentes no modelo do termostato sobre as variáveis física do sistema.
Método
Termostato de Nosé
Para entender o termostado de Nóse-Hoover, primeiramente será mostrado o termostato de Nosé[2].
Este termostato atribui coordenadas generalizados adicionais Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s } e o seu momento conjugado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_s } ao banho térmico. O fator Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s } é definido como um fator de escala das velocidades, onde:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold v = s\dot \bold r = s\bold p/m}
E também são definidas as energia potenciais e cinética associadas a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s } como:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal U_s = (N_f + 1)k_BT \ln(s) }
e
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal K_s = \frac{1}{2}Q\dot s^2 = \frac{p_s^2}{2Q} }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } é entendido como a "inércia térmica", ele determina a escala do tempo da flutuação de temperatura.
O Lagrangiano do sistema extendida (consistente das partículas e do banho térmico) então é postulado como:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal L = \mathcal K + \mathcal K_s - \mathcal U - \mathcal U_s = \sum_i \frac{\bold p_i^2}{2m_is^2} + \frac{p_s^2}{2Q} - \mathcal U(\bold r) - (N_f + 1)k_BTln(s)} .
Como não é explicitamente dependente do tempo:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal H_N = \mathcal K + \mathcal K_s + \mathcal U + \mathcal U_s = \sum_i \frac{\bold p_i^2}{2m_is^2} + \frac{p_s^2}{2Q} + \mathcal U(\bold r) + (N_f + 1)k_BTln(s)} .
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal H_N } se conserva. [3].
Assim, as equações de movimento podem ser deduzidas:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold \dot r_i = \frac{\partial \mathcal H_N}{\partial \bold p_i} = \frac{\bold p_i}{m_is^2}}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold \dot p = -\frac{\partial \mathcal H_N}{\partial \bold r_i} = \bold f_i}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot s = \frac{\partial \mathcal H_N}{\partial p_s} = p_s/Q}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot p_s = -\frac{\partial \mathcal H_N}{\partial s} = \sum_i \frac{\bold p_i^2}{m_is^3} - (N_f + 1)k_BT/s }
Assim, para tempos longos, o termostato de Nosé pode ser tratado como um sistema de partículas junto a um banho térmico, ou seja, como um ensemble canônico. Entretanto, o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } precisa ser determinado por tentativa e erro. Outro problema do termostato de Nosé é o fato de que, por as velocidades serem escaladas com o Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s } , o tempo também será escalado com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s } , o que não acontece em sistemas reais e extendidos. [3]
Termostato de Nosé-Hoover
Para contornar esses problemas, Hoover utilizou uma parametrização diferente, sem o termo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s. } [4]. O parâmetro Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s } pode ser removido das equações reescrevendo-as utilizando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold r } , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold \dot r } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold \ddot r } . Assim, as equações de movimento do termostato de Nosé-Hoover são:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold \dot r = \dot p_i/m_i}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold \dot p = \bold f_i - \xi \bold p_i = \bold f_i \frac{p_\eta}{Q}\bold p_i }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot \eta = p_\eta/Q }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot p_\eta = \sum_i \frac{\bold p_i^2}{m_i} - N_fk_BT }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta } agora são os termos relacionados à fricção do banho térmico.
Cadeias de Nosé-Hoover
O termostato de Nosé-Hoover gera distribuição canônica quando não há forças externas ao sistema. Enquanto existem sistemas com forças externas que podem apresentar este comportamento, existem casos com forças externas onde esse termostato não gera o comportamento esperado. Para contornar esse problema, Martyna et al. [5] propuseram uma solução onde um termostato de Nosé-Hoover está acoplado a outro termostato de Nosé-Hover, formando uma cadeia. Este sistema ainda irá gerar uma distribuição canônica e não apresentará problemas com forças externas. As equações de movimento para um sistema com M termostatos são:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold \dot r_i = \frac{\bold p_i}{m_i} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold f_i - \frac{p_{\xi 1}}{Q_1}\bold p_i }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot \xi_k = \frac{p_{\xi,k}}{q_k} \quad k=1,...,M }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot p_{\xi, 1} = \left(\sum_i\frac{p_i^2}{m_i} - Lk_BT\right) - \frac{p_{\xi,2}}{Q_2}p_{\xi,1} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot p_{\xi, k} = \left[\frac{p_{\xi_{k-1}}^2}{Q_{k-1}} - k_BT\right] - \frac{p_{\xi_{k+1}}}{Q_{k+1}} }
. . .
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot p_{\xi, M} = \left[\frac{p_{\xi_{M-1}}^2}{Q_{M-1}} - k_BT\right] }
Que serão as equações utilizadas para a este trabalho, utilizando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle M=2 } .
Objetivos
Utilizando o termostato de Nosé-Hoover, serão feitos gráficos utilizando diferentes valores de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } , a fim de analisar qual é o efeito dessa variável sobre o sistema. Para melhor análise, primeiramente o sistema será estabilizado com a temperatura Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 1.0 } , e então terá um pulo na temperatura para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 1.5 } , com isso será possível analisar qual é o efeito da inércia térmica do banho térmico do sistema.
Serão feitos gráficos da temperatura ao longo do tempo de simulação, onde será possível observar as flutuações que ocorrem no sistema, além de um gráfico para mostrar a depedência da velocidade das partículas de acordo com o Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } escolhido. Este trabalho é baseado no Case Study 11 do livro "Understanding Molecular Simulation" - Daan Frenkel e Berend Smit: "Lennard-Jones: Nosé-Hoover Termostat"
Resultados
Temperatura constante
Primeiramente, foi feita uma simulação, com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 1.0 } constante ao longo de toda simulação utilizando três diferentes valores para a inércia do banho térmico, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q = 0.1 } (que será chamado de "Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } baixo"), Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q = 1.0 } ("Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } intermediário") e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q = 10.0 } ("Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } alto"), conforme visto nas figuras 1, 2 e 3. É notável que existem intensas oscilações na temperatura no início da simulação para cada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } utilizado, devido ao tempo que o sistema leva para atingir o equilíbrio. Além disso, as oscilações se mantém ao longo de toda simulação.
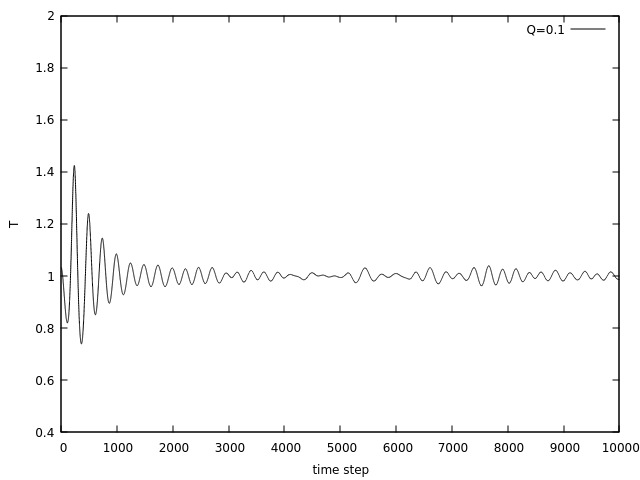
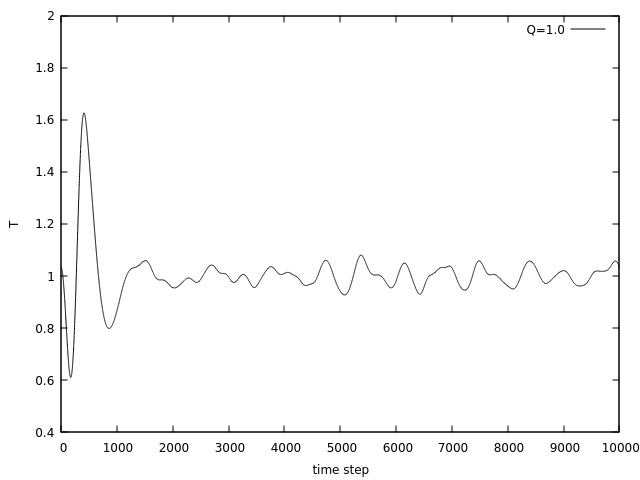
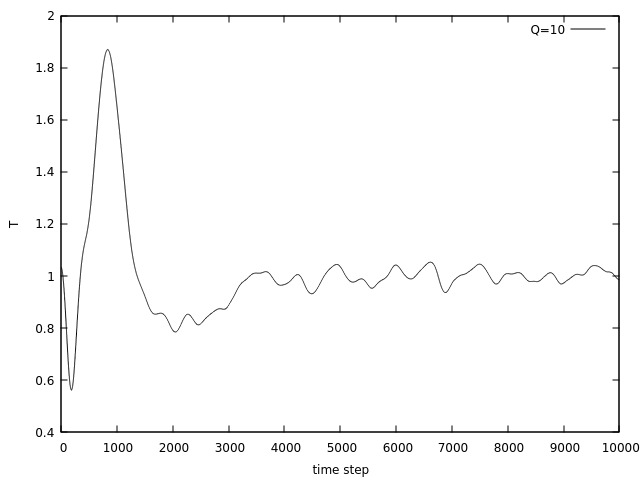
Na figura 4 vemos, diretamente, a diferença causada pelos diferentes valores de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } . Para um Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } baixo, existem oscilações pouco intensas mas de maior frequência, para um Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } alto o sistema tende para a temperatura desejada sem muitas oscilações. O comportamento do Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } intermediário se encontra entre os dois valores de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } testados.
Salto de temperatura
Abaixo são demonstradas situações onde houve um salto da temperatura de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 1.0 } para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 1.5 } a partir do passo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 12000 } (esse valor foi escolhido para ter certeza que o sistema já se encontrava no equílibrio neste instante), utilizando os mesmos três diferentes valores da variável referente a inércia do banho térmico do exemplo acima.
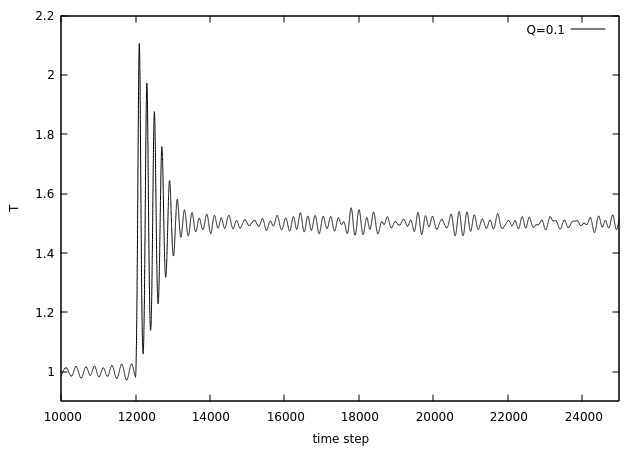
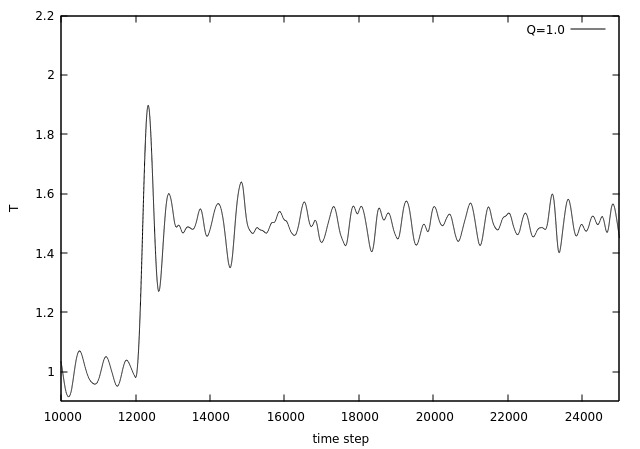
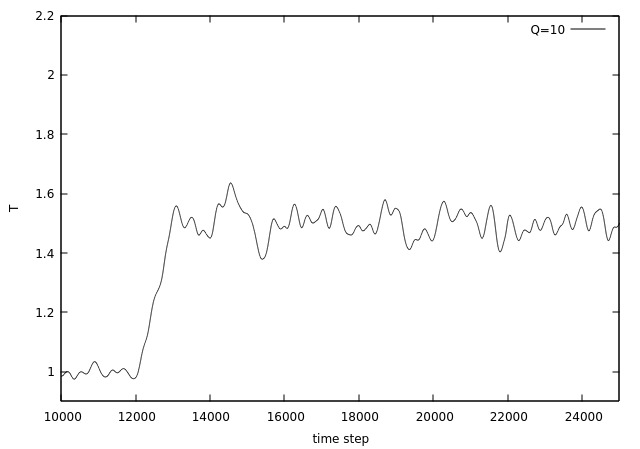
O que nota-se neste resultado, e que fica mais claro na figura 8, é que para um valor de baixo, ou seja, baixa inércia térmica, a temperatura do sistema possui muitas oscilações quando acontece o pulo, logo o sistema demora mais para se estabilizar, entretanto, quando estabilizado as oscilações são menores do que para valores de maiores. Para um alto, a temperatura não oscila depois do pulo, tendendo rapidamente para o valor desejado, entretanto, possuindo oscilações maiores do que para um Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } baixo. O resultado de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } intermediário apresenta um comportamento entre os outros dois resultados, apresentando oscilações após o pulo, mas rapidamente tendendo para o valor desejado.
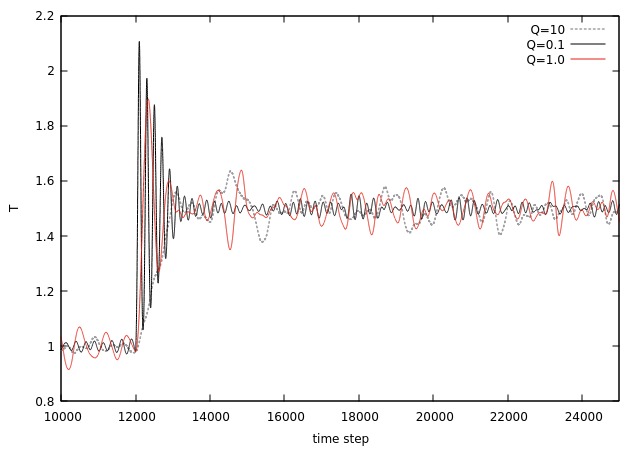
Conforme visto, o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } influência o equilíbrio do sistema, portanto, conforme dito anteriormente, este valor precisa ser determinado, para cada sistema, por tentativa e erro.
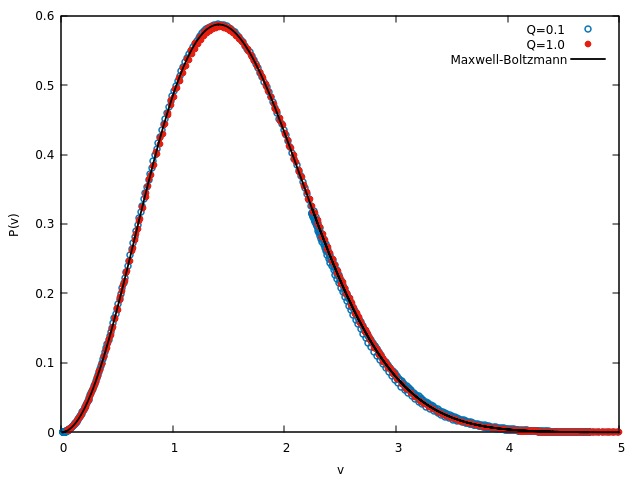
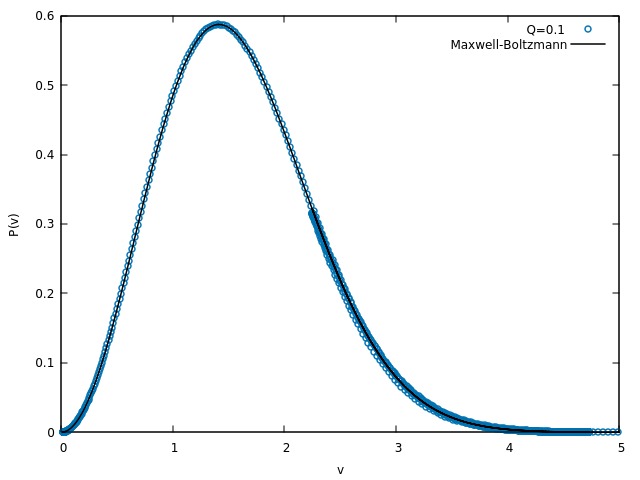
Entretanto, o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } não pode afetar as propriedades físicas da partícula, como a velocidade. Visto que a velocidade da partícula, ou seja, a temperatura média do sistema, é independente de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } , um gráfico da distribuição de Maxwell-Boltzmann para cada situação tem de ser idêntico à todos outros valores de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } . Isso é demonstrado nas figuras abaixo.

Conclusões e Perspectivas Futuras
Com o trabalho apresentado, foi possível utilizar o termostato de Nosé-Hoover para fazer análise do sistema proposto. Entrentanto ainda é necessário expandir este trabalho além de melhorias que poderiam ser feitas, como o cálculo do deslocamento quadrado médio das partículas no banho térmico.
Programas Utilizados
Programa sem o salto de temperatura
/*********************************************/
// Simulação de DM de um fluido de Lennard-Jones com termostato Nosé-Hoover Compile usando "gcc -o NVT_NH NVT_NH.c -lm -lgsl" //
/********************************************/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <gsl/gsl_rng.h>
#include <gsl/gsl_randist.h>
/*********CONSTANTES GLOBAIS #1*****************/
#define rho 0.75 //Densidade
#define V N*1./rho //Volume
#define N 256 //Numeros de particulas
#define T0 0.0
#define M 2 //Numero de correntes Nosé-Hoover
#define TEMPO_MAX 10000 //Tempo de simulação
/*********VARIAVEIS GLOBAIS******************/
double rx[N],ry[N],rz[N];
double vx[N],vy[N],vz[N];
double xi1[N],xi2[N],vxi1[N],vxi2[N];
double fx[N],fy[N],fz[N];
double Q1[M],Q2[M];// "Massa" de resistencia do Termostato
double uk,pe; // Energia cinetica e potencial
double T;
double et, et0,r2;
/*********CONSTANTES GLOBAIS #2******************/
double l=3*N;// Variaveis reais - Frenkel --> L=3N
double L = pow(V,1./3.);//Comprimento da aresta da caixa
double delt=0.0002, delt2, delt4, delt8;
double To = 1.0;//Temperatura de interesse
/********************FUNÇÕES*********************/
void init(void);
void force(void);
void chain(double T);
void aplica_PBC(void);
/********************************************/
gsl_rng * r;// Gerador global
/****INCIAR AS POSIÇÕES E VELOCIDADES********/
void init ( void)
/*******************************************/
{
int i;
double cmvx=0.0,cmvy=0.0,cmvz=0.0;
double fac;
double dx,dy,dz;
int M1,n1;
unsigned long int Seed = 23410981;
gsl_rng_set(r,Seed);
uk=0;
n1=ceil(pow(N,1./3.));
M1=pow(n1,3);
dx=pow(V/M1,(1./3.));
dy=pow(V/M1,(1./3.));
dz=pow(V/M1,(1./3.));
for (i=0;i<N;i++)
{
rx[i] = (i%n1)*dx;
ry[i] = ((i/n1)%n1)*dy;
rz[i] = ((i/(n1*n1))%n1)*dz;
// Velocidade aleatoria de distribuição normal
vx[i]=gsl_ran_gaussian(r,1.0);
vy[i]=gsl_ran_gaussian(r,1.0);
vz[i]=gsl_ran_gaussian(r,1.0);
cmvx+=vx[i];
cmvy+=vy[i];
cmvz+=vz[i];
vx[i]-=cmvx/N;
vy[i]-=cmvy/N;
vz[i]-=cmvz/N;
uk+=(vx[i]*vx[i]+vy[i]*vy[i]+vz[i]*vz[i])/2;// Energia cinética média
}
/********************************************/
if (T0>0.0)
{
T = (2/3)*(uk/N);// Temperatura do sistema
fac=sqrt(T0/T);
for (i=0;i<N;i++)
{
vx[i]*=fac;
vy[i]*=fac;
vz[i]*=fac;
uk+= (vx[i]*vx[i]+vy[i]*vy[i]+vz[i]*vz[i])/2;
}
}
return;
}
/*********CALCULAR FORÇAS******************/
void force(void)
/*******************************************/
{
int i,j;
double dx, dy, dz,r2i, r6i;
double ff,rc,rc2;
double ecut;
pe = 0.0;
rc = L/2;
rc2 = rc*rc;
ecut = 4*(pow(rc2,-6)-pow(rc2,-3));
for (i=0;i<N;i++)
{
fx[i]=0.0;
fy[i]=0.0;
fz[i]=0.0;
}
for (i=0;i<(N-1);i++)
{
for (j=i+1;j<N;j++)
{
dx = (rx[i]-rx[j]);
dy = (ry[i]-ry[j]);
dz = (rz[i]-rz[j]);
dx=dx-rint(dx/L)*L;
dy=dy-rint(dy/L)*L;
dz=dz-rint(dz/L)*L;
r2 = dx*dx + dy*dy + dz*dz;
if (r2<rc2)
{
r2i = 1.0/r2;
r6i = r2i*r2i*r2i;
ff = 48.0*r6i*r2i*(r6i-0.5);
fx[i] += dx*ff;
fx[j] -= dx*ff;
fy[i] += dy*ff;
fy[j] -= dy*ff;
fz[i] += dz*ff;
fz[j] -= dz*ff;
pe+= 4.0*r6i*(r6i - 1.0) - ecut;//Energia potencial
}
}
}
return;
}
/*******************************************/
void chain ( double T)
/*******************************************/
{
double G1, G2, s;
int i;
Q1[0] = 10;//1.0//0.1
Q2[1] = 10;//1.0//0.1
delt2 = delt/2;
delt4 = delt/4;
delt8 = delt/8;
G2= (Q1[0]*vxi1[0]*vxi1[0]-T);
vxi2[1]= vxi2[1] + G2*delt4;
vxi1[0]=vxi1[0]*exp(-vxi2[1]*delt8);
G1=(2*uk-l*T)/Q1[0];
vxi1[0]=vxi1[0] + G1*delt4;
vxi1[0]=vxi1[0]*exp(-vxi2[1]*delt8);
xi1[0]=xi2[0] + vxi1[0]*delt2;
xi2[1]=xi2[1] + vxi2[1]*delt2;
s=exp(-vxi1[0]*delt2);
for (i=0;i<N;i++)
{
vx[i]=s*vx[i];
vy[i]=s*vy[i];
vz[i]=s*vz[i];
}
uk = uk*s*s;
vxi1[0]=vxi1[0]*exp(-vxi2[1]*delt8);
G1=(2*uk-l*T)/Q1[0];
vxi1[0]=vxi1[0] + G1*delt4;
vxi1[0]=vxi1[0]*exp(-vxi2[1]*delt8);
G2=(Q1[0]*vxi1[0]*vxi1[0]-T)/Q2[1];
vxi2[1]=vxi2[1] + G2*delt4;
return;
}
void aplica_PBC(void)
{
int i;
for(i=0;i<N;i++)
{
if(rx[i]>L)
{
rx[i] = rx[i] - 1.0*L;
}
else if (rx[i]<0) {
rx[i] = rx[i] + 1.0*L;
}
if(ry[i]>L)
{
ry[i] = ry[i] - 1.0*L;
}
else if (ry[i]<0) {
ry[i] = ry[i] + 1.0*L;
}
if(rz[i]>L)
{
rz[i] = rz[i] - 1.0*L;
}
else if (ry[i]<0)
{
rz[i] = rz[i] + 1.0*L;
}
}
return;
}
/*******************************************/
/*******************************************/
int main ( void )
/*******************************************/
{
int i;
double t;
const gsl_rng_type * A;
gsl_rng_env_setup();
A = gsl_rng_default;
r = gsl_rng_alloc (A);
init();
/*******************************************/
for (t=0;t<TEMPO_MAX;t++)
{
chain(To);
/******************************************/
uk = 0.0;
for (i=0;i<N;i++)
{
rx[i]+=vx[i]*delt2;
ry[i]+=vy[i]*delt2;
rz[i]+=vz[i]*delt2;
}
aplica_PBC();
/************Calculo das Forças**************/
force();
/********************************************/
for (i=0;i<N;i++)
{
vx[i]+=delt*fx[i];
vy[i]+=delt*fy[i];
vz[i]+=delt*fz[i];
rx[i]+=vx[i]*delt2;
ry[i]+=vy[i]*delt2;
rz[i]+=vz[i]*delt2;
uk+=(vx[i]*vx[i]+vy[i]*vy[i]+vz[i]*vz[i])/2;
}
chain(To);
T = (2/3.)*(uk/N);
et = pe + uk;
/*Tempo,ENERGIA(Potencial,Cinetica,Total) e Temperatura*/
printf("%lf\t%lf\t%lf\t%lf\t%lf\n", t,pe,uk,et,T);
/********************************************/
}
return 0;
}
Programa com o salto de temperatura
/*********************************************/
// Simulação de DM de um fluido de Lennard-Jones com termostato Nosé-Hoover Compile usando "gcc -o NVT_NH NVT_NH.c -lm -lgsl" //
/********************************************/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <gsl/gsl_rng.h>
#include <gsl/gsl_randist.h>
/*********CONSTANTES GLOBAIS #1*****************/
#define rho 0.75 //Densidade
#define V N*1./rho //Volume
#define N 256 //Numeros de particulas
#define T0 0.0
#define M 2 //Numero de correntes Nosé-Hoover
#define TEMPO_MAX 30000 //Tempo de simulação
/*********VARIAVEIS GLOBAIS******************/
double rx[N],ry[N],rz[N];
double vx[N],vy[N],vz[N];
double xi1[N],xi2[N],vxi1[N],vxi2[N];
double fx[N],fy[N],fz[N];
double Q1[M],Q2[M];// "Massa" de resistencia do Termostato
double uk,pe; // Energia cinetica e potencial
double T;
double pe, et, et0,r2;
/*********CONSTANTES GLOBAIS #2******************/
double l=3*N;// Variaveis reais - Frenkel --> L=3N
double L = pow(V,1./3.);//Comprimento da aresta da caixa
double delt=0.0002, delt2, delt4, delt8;
double To = 1.0;//Primeira temperatura de interesse
double tempo_p=12000; // Tempo do pulo de temperatura
double Temp_p=1.5;//Segundo temperatura de interesse
/********************FUNÇÕES*********************/
void init(void);
void force(void);
void chain(double T);
void aplica_PBC(void);
/********************************************/
gsl_rng * r;// Gerador global
/****INCIAR AS POSIÇÕES E VELOCIDADES********/
void init ( void)
/*******************************************/
{
int i;
double cmvx=0.0,cmvy=0.0,cmvz=0.0;
double fac;
double dx,dy,dz;
int M1,n1;
unsigned long int Seed = 23410981;
gsl_rng_set(r,Seed);
uk=0;
n1=ceil(pow(N,1./3.));
M1=pow(n1,3);
dx=pow(V/M1,(1./3.));
dy=pow(V/M1,(1./3.));
dz=pow(V/M1,(1./3.));
for (i=0;i<N;i++)
{
rx[i] = (i%n1)*dx;
ry[i] = ((i/n1)%n1)*dy;
rz[i] = ((i/(n1*n1))%n1)*dz;
// Velocidade aleatoria de distribuição normal
vx[i]=gsl_ran_gaussian(r,1.0);
vy[i]=gsl_ran_gaussian(r,1.0);
vz[i]=gsl_ran_gaussian(r,1.0);
cmvx+=vx[i];
cmvy+=vy[i];
cmvz+=vz[i];
vx[i]-=cmvx/N;
vy[i]-=cmvy/N;
vz[i]-=cmvz/N;
uk+=(vx[i]*vx[i]+vy[i]*vy[i]+vz[i]*vz[i])/2;// Energia cinética média
}
/********************************************/
if (T0>0.0)
{
T = (2/3)*(uk/N);// Temperatura do sistema
fac=sqrt(T0/T);
for (i=0;i<N;i++)
{
vx[i]*=fac;
vy[i]*=fac;
vz[i]*=fac;
uk+= (vx[i]*vx[i]+vy[i]*vy[i]+vz[i]*vz[i])/2;
}
}
return;
}
/*********CALCULAR FORÇAS******************/
void force(void)
/*******************************************/
{
int i,j;
double dx, dy, dz,r2i, r6i;
double ff,rc,rc2;
double ecut;
pe = 0.0;
rc = L/2;
rc2 = rc*rc;
ecut = 4*(pow(rc2,-6)-pow(rc2,-3));
for (i=0;i<N;i++)
{
fx[i]=0.0;
fy[i]=0.0;
fz[i]=0.0;
}
for (i=0;i<(N-1);i++)
{
for (j=i+1;j<N;j++)
{
dx = (rx[i]-rx[j]);
dy = (ry[i]-ry[j]);
dz = (rz[i]-rz[j]);
dx=dx-rint(dx/L)*L;
dy=dy-rint(dy/L)*L;
dz=dz-rint(dz/L)*L;
r2 = dx*dx + dy*dy + dz*dz;
if (r2<rc2)
{
r2i = 1.0/r2;
r6i = r2i*r2i*r2i;
ff = 48.0*r6i*r2i*(r6i-0.5);
fx[i] += dx*ff;
fx[j] -= dx*ff;
fy[i] += dy*ff;
fy[j] -= dy*ff;
fz[i] += dz*ff;
fz[j] -= dz*ff;
pe+= 4.0*r6i*(r6i - 1.0) - ecut;//Energia potencial
}
}
}
return;
}
/*******************************************/
void chain ( double T)
/*******************************************/
{
double G1, G2, s;
int i;
Q1[0] = 10;//0.1/1.0
Q2[1] = 10;//0.1//1.0
delt2 = delt/2;
delt4 = delt/4;
delt8 = delt/8;
G2= (Q1[0]*vxi1[0]*vxi1[0]-T);
vxi2[1]= vxi2[1] + G2*delt4;
vxi1[0]=vxi1[0]*exp(-vxi2[1]*delt8);
G1=(2*uk-l*T)/Q1[0];
vxi1[0]=vxi1[0] + G1*delt4;
vxi1[0]=vxi1[0]*exp(-vxi2[1]*delt8);
xi1[0]=xi2[0] + vxi1[0]*delt2;
xi2[1]=xi2[1] + vxi2[1]*delt2;
s=exp(-vxi1[0]*delt2);
for (i=0;i<N;i++)
{
vx[i]=s*vx[i];
vy[i]=s*vy[i];
vz[i]=s*vz[i];
}
uk = uk*s*s;
vxi1[0]=vxi1[0]*exp(-vxi2[1]*delt8);
G1=(2*uk-l*T)/Q1[0];
vxi1[0]=vxi1[0] + G1*delt4;
vxi1[0]=vxi1[0]*exp(-vxi2[1]*delt8);
G2=(Q1[0]*vxi1[0]*vxi1[0]-T)/Q2[1];
vxi2[1]=vxi2[1] + G2*delt4;
return;
}
void aplica_PBC(void)
{
int i;
for(i=0;i<N;i++)
{
if(rx[i]>L)
{
rx[i] = rx[i] - 1.0*L;
}
else if (rx[i]<0) {
rx[i] = rx[i] + 1.0*L;
}
if(ry[i]>L)
{
ry[i] = ry[i] - 1.0*L;
}
else if (ry[i]<0) {
ry[i] = ry[i] + 1.0*L;
}
if(rz[i]>L)
{
rz[i] = rz[i] - 1.0*L;
}
else if (ry[i]<0)
{
rz[i] = rz[i] + 1.0*L;
}
}
return;
}
/*******************************************/
int main ( void )
/*******************************************/
{
int i;
double t;
const gsl_rng_type * A;
gsl_rng_env_setup();
A = gsl_rng_default;
r = gsl_rng_alloc (A);
init();
/*******************************************/
for (t=0;t<TEMPO_MAX;t++)
{
/*******************************************/
if (t==tempo_p)
To = Temp_p;
chain(To);
/******************************************/
uk = 0.0;
for (i=0;i<N;i++)
{
rx[i]+=vx[i]*delt2;
ry[i]+=vy[i]*delt2;
rz[i]+=vz[i]*delt2;
}
aplica_PBC();
/************Calculo das Forças**************/
force();
/********************************************/
for (i=0;i<N;i++)
{
vx[i]+=delt*fx[i];
vy[i]+=delt*fy[i];
vz[i]+=delt*fz[i];
rx[i]+=vx[i]*delt2;
ry[i]+=vy[i]*delt2;
rz[i]+=vz[i]*delt2;
uk+=(vx[i]*vx[i]+vy[i]*vy[i]+vz[i]*vz[i])/2;
}
chain(To);
T = (2/3.)*(uk/N);
et = pe + uk;
/*Tempo,ENERGIA(Potencial,Cinetica,Total) e Temperatura*/
printf("%lf\t%lf\t%lf\t%lf\t%lf\n", t,pe,uk,et,T);
/********************************************/
}
return 0;
}
Referências
- ↑ https://www2.ph.ed.ac.uk/~dmarendu/MVP/MVP03.pdf
- ↑ NOSÉ, Shuichi, A molecular dynamics method for simulations in the canonical ensemble, Molecular Physics, 1984, Vol. 52, No. 2, 255-268
- ↑ 3,0 3,1 http://www.courses.physics.helsinki.fi/fys/moldyn/lectures/L5.pdf
- ↑ William G. Hoover, Canonical Dynamics: Equilibrium phase-space distributions, Physical Review A, 1985, Vol. 31, No. 3.
- ↑ MARTYNA, G. J., KLEIN, M. L., TUCKERMAN, M. Nosé-Hoover chains: The canonical ensemble via continuous dynamics J. Chem. Phys. 1992, Vol. 97 No. 4.