Simulação de Micélio de Fungo: mudanças entre as edições
Sem resumo de edição |
|||
| (296 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
'''Grupo: Arthur Dornelles, Bruno Zanette, Gabriel De David e Guilherme Hoss''' | '''Grupo: Arthur Dornelles, Bruno Zanette, Gabriel De David e Guilherme Hoss''' | ||
O objetivo deste trabalho é modelar computacionalmente o desenvolvimento de micélios em fungos com base em mecanismos gerais pré-estabelecidos. O progresso e a complexidade dos modelos cresceram de maneira gradual ao longo do trabalho através de | O objetivo deste trabalho é modelar computacionalmente o desenvolvimento de micélios em fungos com base em mecanismos gerais pré-estabelecidos buscando a criação de estruturas similares com micélios reais. O progresso e a complexidade dos modelos cresceram de maneira gradual ao longo do trabalho através de diferentes modelos de crescimento. O trabalho foi inspirado - principalmente - nos dois primeiros capítulos do artigo de Steven Hopkins <ref name='HOPKINS'>S. Hopkins. A Hybrid Mathematical Model of Fungal Mycelia: Tropisms, Polarised Growth and Application to Colony Competition, tese de doutorado, 2011.(https://core.ac.uk/download/pdf/6117416.pdf) </ref>. | ||
== | == Motivação e Introdução aos Fungos == | ||
[[Arquivo:fungo.jpg|250px|thumb|left|'''Figura 1''': Ilustração da estrutura de um fungo. <ref name='PAULA'> P. L. Moraes. Fungos. Mundo Educação. Disponível em: https://mundoeducacao.uol.com.br/biologia/os-fungos.htm. Acesso em: 15 de Maio de 2021. </ref>.]] | |||
[[Arquivo:ramifica.png|250px|thumb|right|'''Figura 2''': Processos de ramificação de fungos. À esquerda a ramificação dicotômica (''Dichotomous'') e à direita o processo de ramificação lateral <ref name='HOPKINS'></ref>.]] | |||
= | Fungos estão integrados em grande parte dos ecossistemas do planeta e cumprem importantes funções na manutenção e sobrevivência dos mesmos. De maneira geral, eles produzem enzimas que são responsáveis pela decomposição de matéria orgânica e - portanto - a reciclagem de diversos nutrientes do ambiente ao seu redor <ref name='SILVA'> P. da Silva. Reino Fungi. Info Escola (2018). Disponível em: https://www.infoescola.com/biologia/reino-fungi. Acesso em: 15 de Maio de 2021. </ref>. Em muitos casos, fungos formam fusões simbióticas com plantas ou algas e interagem de diferentes maneiras com diferentes organismos vivos. Neste trabalho, todavia, não faremos a análise dessas interações e focaremos no comportamento individual de crescimento de fungos. | ||
Anatomicamente, fungos são compostos por células que se assemelham a tubos microscópicos, denominadas de '''hifas'''. Essas hifas então se ramificam e se fundem umas com as outras em um processo chamado de '''anastomose''', formando uma complexa rede chamada de '''micélio''' ('''figura 1'''). | |||
A criação de novas hifas, em geral, ocorre ao longo do tempo através de dois processos principais: o primeiro, denominado de '''ramificação dicotômica''', consiste na ponta de uma hifa já existente se dividindo ao meio. O segundo processo é chamado de '''ramificação lateral''', no qual, como o nome sugere, formam-se novos ramos e hifas na lateral de uma hifa já existente, como pode ser visto na '''figura 2'''. | |||
Tendo em vista o objetivo deste trabalho, é importante também entender o porquê e quando as ramificações citadas acimas ocorrem, para que possamos programá-las em nosso modelo computacional. A ramificação, portanto, é atribuída ao acúmulo de partículas de nutrientes e materiais no ambiente, o que estimula a extensão das hifas dos fungos em sua direção. Dessa maneira, '''o crescimento e desenvolvimento dos fungos são altamente dependentes e influenciados pela disponibilidade de nutrientes e materiais no ambiente ao seu redor'''. Apesar desse fato, fungos podem continuar se desenvolvendo até em ambientes com poucos nutrientes, devido ao processo de '''translocação''', no qual os nutrientes previamente absorvidos pelo fungo podem ser transportados internamente, bancando o crescimento do mesmo em locais com deficiência de nutrientes <ref name='HOPKINS'></ref>. | |||
== Mecanismos Gerais dos Modelos == | |||
Um dos grandes obstáculos com a programação de um modelo biológico com variáveis discretas é o processamento de grandes quantidades de dados. Conforme o tempo de simulação aumenta e as redes de hifas se tornam maiores e mais complexas, a quantidade de informação processada aumenta exponencialmente e, devido a esse fato, algumas características típicas do desenvolvimento de fungos citadas na primeira seção foram deixadas de lado para a construção de nosso modelo computacional (como a ramificação lateral e a translocação). No entanto, os mecanismos essenciais para o bom funcionamento da simulação foram mantidos e serão abordados mais profundamente nessa seção. | |||
===Crescimento=== | ===Crescimento=== | ||
Fungos possuem - nas pontas de suas hifas - uma estrutura chamada de Spitzenkörper (''corpo superior'' em alemão). Essa estrutura possui a função de orientar a hifa em seu crescimento e de transformar todo o material de crescimento (nutriente) encontrado em material para as paredes de seus tubos, o que leva à expansão de tamanho do fungo <ref name='SPITZEN'> G. Steinberg (2007). "Hyphal growth: a tale of motors, lipids, and the Spitzenkörper". Eukaryotic Cell. 6 (3): 351–360. doi:10.1128/EC.00381-06 </ref>. | |||
Por isso, tipicamente, as hifas dos fungos crescem de maneira apical (em suas pontas) e em linha reta, possuindo baixa variação em sua orientação e, quando há variação, as mudanças no ângulo de crescimento ocorrem devido a um deslocamento do Spitzenkörper. Estudos anteriores demonstram que essas variações na angulação são - para certas espécies - normalmente distribuídas <ref name= 'crescimento'> Molin, P., P. Gervais, J. Lemiere, and T. Davet (1992). Direction of hyphal growth: a relevant | |||
parameter in the development of filamentous fungi. Research in Microbiology 143, 777–784. doi: 10.1016/0923-2508(92)90106-x. </ref>. A espécie ''Mucor hiemalis'', por exemplo, possui uma angulação média de 56° e desvio padrão de 17° <ref name=Hutch> Hutchinson, S. A., P. Sharma, K. R. Clarke, and I. Macdonald (1980). Control of hyphal orientation in colonies of Mucor hiemalis. Transactions of the British Mycological Society 75, | |||
177–191. doi: 10.1016/S0007-1536(80)80078-7 </ref>. | |||
Como comentado anteriormente, a concentração de substrato (nutrientes) presente no local da ponta da hifa irá determinar se a expansão da mesma irá ocorrer ou não. Por isso, computacionalmente, a extensão das hifas é modelada de maneira que a concentração de nutrientes na ponta de um hifa arbitrária é checada e, caso haja substrato o suficiente (é determinado um limiar de acordo com a espécie de fungo), o crescimento da hifa segue adiante, caso contrário ele permanece estagnado. Além disso, a orientação do ângulo de crescimento é dependente da orientação inicial da hifa e de um fator aleatório dependente da espécie a ser analisada. | |||
[[Arquivo:anastosomose.png|250px|thumb|right|'''Figura 3''': O processo de anastomose pode ocorrer de duas maneiras distintas. À esquerda, anastomose de duas pontas separadas (''Tip to Tip Anastomosis''). À direita, a anastomose de uma ponta com uma hifa (''Tip to Hypha Anastomosis)'' <ref name='HOPKINS'></ref>.]] | |||
===Divisão e Anastomose=== | |||
Os dois tipos de divisões - ou ramificações - citadas anteriormente na seção introdutória variam entre as diferentes espécies de fungo e - da mesma maneira que o crescimento por expansão das hifas - são altamente dependentes da alta concentração de nutrientes em seu ambiente. Além disso, a absorção de novos nutrientes através do Spitzenkörper resulta em uma pressão de Turgor (ou pressão hidrostática) nas paredes internas do fungo, o que também influencia diretamente no processo de ramificação das hifas <ref name='HOPKINS'></ref>. Conforme o crescimento do fungo ocorre e suas ramificações acontecem, o processo de encontro e fusão das pontas das hifas dos fungos citado na primeira seção (anastomose) começa a ocorrer. Este processo também pode ocorrer de diferentes maneiras, como pode ser visto na '''figura 3'''. Após a ocorrência de ambos os processos, as hifas - agora juntas umas das outras - passam a permitir a transmissão de substâncias internamente entre si. Computacionalmente e de maneira similar ao crescimento, as divisões também dependem da quantidade de nutrientes presentes no local de possível ramificação e - além disso - dependem de um fator de ângulo aleatório que varia com a espécie simulada. A anastomose, por outro lado, possui uma programação mais complexa e utiliza o método de intersecção de linhas, que será mais aprofundado na próxima seção. | |||
== Formulação Matemática e Implementação == | |||
O código base que chama as funções é o seguinte: | |||
<source lang="python"> | |||
flag = True | |||
# xi yi xf yf flag | |||
eventos = np.array( [[ 0, 0, 1, 0, True]] ) | |||
for i in range (1,8): | |||
eventos = np.append( eventos, [[ 0, 0, r * math.cos(np.pi/4 *i), r * math.sin(np.pi/4*i), True]], axis=0) | |||
for i in range (0,repeticao): | |||
try: | |||
if not eventos[i][4]: | |||
continue | |||
except IndexError or Exception: | |||
break | |||
c = check_nutri(eventos[i][2],eventos[i][3],xCOORDENADA_MAPA,yCOORDENADA_MAPA,MAPA_NUTRIENTE) | |||
if (random.random() > 0.6857-0.2857*c and c>=0.3): #faz divisão | |||
custo = 0.3 | |||
c1x,c1y,c2x,c2y= divisao(eventos[i][0],eventos[i][1],eventos[i][2],eventos[i][3]) | |||
c1x,c1y,flag_1 = check_anastomose(eventos, c1x,c1y, eventos[i][2],eventos[i][3]) | |||
c2x,c2y,flag_2 = check_anastomose(eventos,c2x,c2y, eventos[i][2],eventos[i][3]) | |||
novo1 = np.array( [eventos[i][2], eventos[i][3], c1x, c1y, flag_1]) | |||
novo2 = np.array( [eventos[i][2], eventos[i][3], c2x, c2y, flag_2] ) | |||
#xf->xi yf->yi xf yf | |||
eventos = np.append( eventos, [novo1], axis=0) | |||
eventos = np.append( eventos, [novo2], axis=0) | |||
MAPA_NUTRIENTE= atualiza_mapa_nutri(eventos[i][2],eventos[i][3],xCOORDENADA_MAPA,yCOORDENADA_MAPA,MAPA_NUTRIENTE,custo) | |||
elif (c >= 0.01): #faz crescimento | |||
custo = 0.01 | |||
newx,newy = crecimento(eventos[i][0],eventos[i][1],eventos[i][2],eventos[i][3]) | |||
newx,newy,flag = check_anastomose(eventos,newx,newy,eventos[i][2],eventos[i][3]) | |||
novo = np.array( [eventos[i][2], eventos[i][3], newx, newy, flag] ) | |||
eventos = np.append( eventos, [novo], axis=0 ) | |||
MAPA_NUTRIENTE= atualiza_mapa_nutri(eventos[i][2],eventos[i][3],xCOORDENADA_MAPA,yCOORDENADA_MAPA,MAPA_NUTRIENTE,custo) | |||
</source> | |||
Os principais mecanismos são: ''eventos'' que armazena os segmentos de retas com ''xi yi xf yf flag''; ''flag'' representa se ocorreu o processo de anastomose, caso ''flag'' armazene ''False'' o primeiro ''try'' faz o segmento parar de crescer; Dentro do ''for'' principal há um ''if'' e ''else'' que junto da condição ''random.random() > 0.6857-0.2857*c'' faz com que 60% de chance de ocorrer de divisão quando c é igual a 1, pois ''random.random()'' é um valor entre [0,1]. | |||
Utilizando as informações biológicas apresentadas nas seções anteriores, é possível criar funções matemáticas e computacionais para a programação dos aspectos fundamentais de uma simulação de micélio de fungos. | |||
* '''Funções:''' | |||
O Crescimento e divisão dependem do ângulo do segmento originário, uma forma de consegui-lo é através da equação: | |||
<math> \theta = arctan \left(\frac{y_f-y_i}{x_f-x_i}\right) </math> | |||
É importante lembrar que para x negativos deve-se somar <math>\pi</math>. Esse cálculo, nas duas funções, implementa-se assim: | |||
<source lang="python"> | <source lang="python"> | ||
x = x2 - x1 | |||
y = y2 - y1 | |||
theta= np.arctan(y/x) | |||
if (x<0) : | |||
theta= theta+ math.pi | |||
aleatorio_theta = random.normalvariate(0, math.pi/4) # angulo de | |||
theta=theta+aleatorio_theta | |||
</source> | |||
===Crescimento=== | |||
Soma-se este ângulo com um número aleatório normalmente distribuído com média zero e sigma dependente de dados estatísticos advindos da observação do fungo que pretende-se modelar. Agora com o ângulo modificado podemos adquirir um x e y final para o novo segmento com <math> r \cos(\theta) </math> e <math> r \sin(\theta) </math> respectivamente, onde r é uma variável global que representa o tamanho de cada hifa. | |||
<source lang="python"> | |||
def crecimento (x1,y1,x2,y2): | |||
x = x2 - x1 | |||
y = y2 - y1 | |||
theta= np.arctan(y/x) | theta= np.arctan(y/x) | ||
if (x<0) : | if (x<0) : | ||
theta= theta+ math.pi | theta= theta+ math.pi | ||
aleatorio_theta = random. | aleatorio_theta = random.normalvariate(0, math.pi/4) # angulo de | ||
theta=theta+aleatorio_theta | theta=theta+aleatorio_theta | ||
| Linha 42: | Linha 143: | ||
addy = r * math.sin(theta) | addy = r * math.sin(theta) | ||
fx = | |||
fy = | fx = x2 + addx | ||
fy = y2 + addy | |||
return (fx,fy) | return (fx,fy) | ||
| Linha 50: | Linha 153: | ||
</source> | </source> | ||
===Divisão=== | |||
A divisão trabalha com uma ideia similar ao crescimento, porém o ângulo aleatório normalmente distribuído é o ângulo que separa as duas hifas criadas | |||
<source lang="python"> | |||
def divisao (x1,y1,x2,y2): | |||
x = x2 - x1 | |||
y = y2 - y1 | |||
theta= np.arctan(y/x) | |||
if (x<0) : | |||
theta= theta + math.pi | |||
angulodivisao= random.normalvariate(0, math.pi/4) | |||
angulo1= theta- angulodivisao/2 | |||
angulo2= theta+ angulodivisao/2 | |||
addx1 = r * math.cos(angulo1) | |||
addy1 = r * math.sin(angulo1) | |||
addx2= r * math.cos(angulo2) | |||
addy2= r * math.sin(angulo2) | |||
Ax = x2 + addx1 | |||
Ay = y2 + addy1 | |||
Bx = x2 + addx2 | |||
By= y2 +addy2 | |||
return (Ax,Ay,Bx,By) | |||
</source> | |||
===Intersecção de Linhas e Anastomose=== | |||
A cada novo crescimento ou divisão, devemos verificar se há cruzamento entre algumas das linhas. Uma forma de tornar o código mais eficiente seria um algorítimo de detecção de cruzamentos que desconsiderasse alguns segmentos que estão muito longe na hora de calcular. | |||
A interseção <math>P=\{P_x,P_y\}</math> de duas linhas <math>L_1</math> e <math>L_2</math> pode ser definida utilizando determinantes dados dois pontos em cada linha. Portanto, podemos descobrir se a linha <math> L_1 </math> definida por dois pontos distintos <math> (x_1, y_1) </math> e <math> (x_2, y_2) </math>, e a linha <math> L_2 </math> definida por dois pontos distintos <math>(x_3,y_3)</math> e <math>(x_4,y_4)</math> se intersectam calculando as seguintes equações matriciais:<ref name=Wolfram> Weisstein, Eric W. "Line-Line Intersection." From MathWorld Disponível em: http://mathworld.wolfram.com/Line-LineIntersection.html | |||
</ref> | |||
Trata-se as linhas como uma curva de Bézier de primeiro grau: | |||
: <math> | |||
L_1 = \begin{bmatrix}x_1 \\ y_1\end{bmatrix} | |||
+ U_a \begin{bmatrix}x_2-x_1 \\ y_2-y_1\end{bmatrix}, | |||
\qquad | |||
L_2 = \begin{bmatrix}x_3 \\ y_3\end{bmatrix} | |||
+ U_b \begin{bmatrix}x_4-x_3 \\ y_4-y_3\end{bmatrix} | |||
</math> | |||
Onde <math>U_a</math> e <math>U_b</math> são números reais definidos como: | |||
: <math> | |||
U_a = \frac{\begin{vmatrix} x_1-x_3 & x_3-x_4\\y_1-y_3 & y_3-y_4\end{vmatrix}}{\begin{vmatrix} x_1-x_2 & x_3-x_4\\y_1-y_2 & y_3-y_4\end{vmatrix}} = \frac{(x_1 - x_3)(y_3-y_4)-(y_1-y_3)(x_3-x_4)}{(x_1-x_2)(y_3-y_4)-(y_1-y_2)(x_3-x_4)} | |||
</math> | |||
: <math> | |||
U_b = \frac{\begin{vmatrix} x_2-x_1 & x_1-x_3\\y_2-y_1 & y_1-y_3\end{vmatrix}}{\begin{vmatrix} x_1-x_2 & x_3-x_4\\y_1-y_2 & y_3-y_4\end{vmatrix}} = \frac{(x_2 - x_1)(y_1-y_3)-(y_2-y_1)(x_1-x_3)}{(x_1-x_2)(y_3-y_4)-(y_1-y_2)(x_3-x_4)}, | |||
</math> | |||
E o ponto de intersecção: | |||
: <math> | |||
(P_x, P_y)= (x_1 + U_a (x_2-x_1),\; y_1 + U_a (y_2-y_1)) \quad \text{ou} \quad (P_x, P_y) = (x_3 + U_b (x_4-x_3),\; y_3 + U_b (y_4-y_3)) | |||
</math> | |||
O ponto de interseção cai dentro do segmento da primeira linha se <math>0 \leqslant U_a \leqslant 1 </math>, e cai dentro do segmento da segunda linha se <math>0 \leqslant U_b \leqslant 1 </math>. <ref name = Wikipedia> ''Line to line intersection''. Wikipedia, the free encyclopedia. Disponível em: https://en.wikipedia.org/wiki/Line%E2%80%93line_intersection. Acesso em: 20 de Maio de 2021. </ref> | |||
<source lang="python"> | |||
def check_anastomose(eventos,xf,yf,xi,yi): | |||
flag = True | |||
for evento in eventos: | |||
if (xi == evento[2] and yi == evento[3]): | |||
continue | |||
if (xi == evento[0] and yi == evento[1]): | |||
continue | |||
D = (evento[3]-evento[1])*(xf-xi) - (evento[2]-evento[0])*(yf-yi) | |||
uA = ((evento[2]-evento[0])*(yi-evento[1]) - (evento[3]-evento[1])*(xi-evento[0]))/D | |||
uB = ((xf-xi)*(yi-evento[1])-(yf-yi)*(xi-evento[0]))/D | |||
flag = True | |||
if (0<=uA<=1) and (0<=uB<=1): | |||
flag = False | |||
if not flag: | |||
xf, yf = get_intersection_point(uA,xf,yf,xi,yi) | |||
break | |||
return xf,yf, flag | |||
</source> | |||
Os primeiros dois ''if''s identifica se a hifa a qual essa foi originada é quem está sendo calculada. Se não há cruzamento temos que ''flag = False'', o que significa que a hifa pode continuar crescendo, caso haja ponto de intersecção é chamada a ''get_intersection_point'' para encontrar o ponto: | |||
<source lang="python"> | |||
def get_intersection_point(uA,xf,yf,xi,yi): | |||
xf = xi + (uA * (xf-xi)) | |||
yf = yi + (uA * (yf-yi)) | |||
return xf,yf | |||
</source> | |||
===Mapa de Nutrientes=== | |||
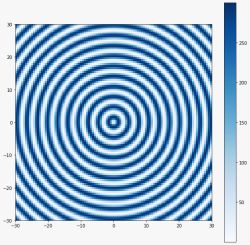
Um mapa de nutriente '''(Figura 4)''' é definido como uma matriz que armazena o valor de nutriente em cada ponto identificado pela matriz ''X'' e ''Y'', o mapa de nutrientes implementado foi um mapa discreto, ao contrário do artigo <ref name='HOPKINS'></ref> que implementou um mapa contínuo. | |||
[[Arquivo:Nutri.png|300px|thumb|right|'''Figura 4''': Exemplo de mapa de nutriente]] | |||
<math> | |||
MN = \left[\begin{matrix} 0.99977783 & 0.97620649 & 0.99977783\\0.97620649 & 0 & 0.97620649 \\ 0.99977783 & 0.97620649 & 0.99977783 \end{matrix}\right] | |||
\quad | |||
X=Y= [\begin{matrix}-30 & 0 & 30\end{matrix}] | |||
</math> | |||
Logo, é necessário encontrar em qual "quadrado" de nutriente a posição do final da hifa está. Para isto usa-se uma função (''find_nearest'') que encontra o valor mais próximo de ''x'' e ''y'' no ''array'' que representa o mapa de nutriente: | |||
<source lang="python"> | |||
def find_nearest(array, value): | |||
array = np.asarray(array) | |||
idx = (np.abs(array - value)).argmin() | |||
return array[idx] | |||
</source> | |||
Portanto, a função ''check_nutri'' que retorna a quantidade de nutrientes disponível utiliza a ''find_nearest'' para encontrar o index do ponto que é também o do nutriente no ponto na matriz ''mapa_nutri'': | |||
<source lang="python"> | |||
def check_nutri(x,y,xmapa,ymapa,mapa_nutri): | |||
near_x = find_nearest(xmapa,x) ## encontra valor mais próximo em x | |||
near_y = find_nearest(ymapa,y) ## encontra valor mais próximo em y | |||
index_x = np.where(xmapa == near_x) ## encontra o index do valor de x | |||
index_y = np.where(ymapa == near_y) ## encontra o index do valor de y | |||
return (mapa_nutri[index_y[0][0]][index_x[0][0]]) | |||
</source> | |||
A função ''atualiza_mapa_nutri'' funciona de maneira similar a ''check_nutri'' porém essa recebe recebe também a variável ''preco'' que representa o custo de uma ação. Para nossa situação as únicas situações que custam nutrientes são o crescimento e a divisão, 0.01 e 0.3 respectivamente. A função então retorna o mapa de nutriente atualizado: | |||
<source lang="python"> | |||
def atualiza_mapa_nutri(x,y,xmapa,ymapa,mapa_nutri,preco): | |||
near_x = find_nearest(xmapa,x) ## encontra valor mais próximo em x | |||
near_y = find_nearest(ymapa,y) ## encontra valor mais próximo em y | |||
index_x = np.where(xmapa == near_x) ## encontra o index do valor de x | |||
index_y = np.where(ymapa == near_y) ## encontra o index do valor de y | |||
mapa_nutri[index_y[0][0]][index_x[0][0]] -= preco | |||
return (mapa_nutri) | |||
</source> | |||
'''Criação do mapa''' | |||
Implementamos três formas de criar o mapa. A função ''mapa_nutri_Nhomogenea'' cria um mapa dependente de uma função que necessariamente deve começar a partir de 0, no caso da função mostrada é <math>\sin(\sqrt{(A^2+B^2)})^2</math>, ela recebe só uma variável para montar um mapa quadrado - com os mesmos números horizontal e verticalmente - e produz o mapa mostrado na '''Figura 9''' | |||
<source lang="python"> | |||
def mapa_nutri_Nhomogenea(x): | |||
A,B=np.meshgrid(x,x) | |||
return (np.sin(np.sqrt(A**2+B**2))**2) | |||
</source> | |||
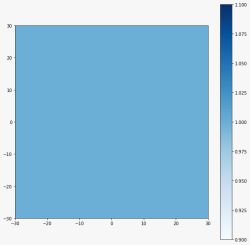
A função ''mapa_unitario_nutri'' cria um mapa homogêneo com todos os nutrientes começando em 1. Exemplo após crescimento do fungo mostrado na '''Figura 13''' | |||
<source lang="python"> | |||
def mapa_unitario_nutri(x): | |||
return (np.ones((len(x),len(x)))) | |||
</source> | |||
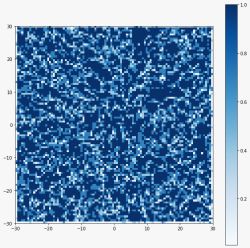
A terceira forma é utilizando uma imagem, como a da '''Figura 5''', que transforma o gradiente de preto a branco dos pontos (''x_mapa,y_mapa'') em um mapa de nutriente, mostrado '''Figura 6''', Preto representa 0 nutriente e branco 1. | |||
[[Arquivo:OBRIGADO.png|200px|thumb|left|Figura 5: imagem de input para criação do mapa de nutrientes]] | |||
[[Arquivo:Mapaonrigadp.png|200px|thumb|right|Figura 6: imagem de output para criação do mapa de nutrientes]] | |||
<source lang="python"> | |||
import cv2 | |||
import numpy as np | |||
import sys | |||
import seaborn as sn | |||
img_path = '/content/OBRIGADO.png' | |||
img = cv2.imread(img_path, 0) # read image as grayscale. Set second parameter to 1 if rgb is required | |||
img_reverted= cv2.bitwise_not(img) | |||
new_img = img_reverted / 255.0 # now all values are ranging from 0 to 1, where white equlas 0.0 and black equals 1.0 | |||
for i in range (0,len(new_img)): | |||
for j in range (0,len(new_img[0])): | |||
new_img[i][j]=-(new_img[i][j]-1) | |||
x_mapa = np.linspace(-80,80,int(len(new_img[0])/1)) | |||
y_mapa = np.linspace(-80,80,int(len(new_img)/1)) | |||
np.set_printoptions(threshold=sys.maxsize) | |||
sn.heatmap(new_img) | |||
xCOORDENADA_MAPA= x_mapa | |||
yCOORDENADA_MAPA= y_mapa | |||
MAPA_NUTRIENTE = new_img | |||
</source> | |||
===Condições Iniciais=== | |||
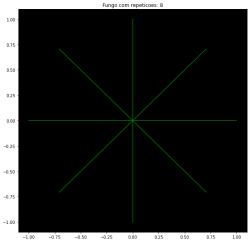
[[Arquivo:CondiIni.png|250px|thumb|right|'''Figura 7''': Condições iniciais]] | |||
As condições iniciais em formato de estrela são mostradas na '''Figura 7''' e implementadas assim: | |||
<source lang="python"> | |||
eventos = np.array( [[ 0, 0, 1, 0, True]] ) # xi yi xf yf flag | |||
for i in range (1,8): | |||
eventos = np.append( eventos, [[ 0, 0, r * math.cos(np.pi/4 *i), r * math.sin(np.pi/4*i), True]], axis=0) | |||
</source> | |||
== Discussão de Resultados == | |||
Como discutido anteriormente o mapa de nutrientes utilizado nas simulações de crescimento das hifas interfere diretamente no resultado final referente ao formato do micélio gerado. Para exemplificar essa diferença executamos 3 simulações utilizando cada um dos três estilos de mapas mostrados já citados, o Mapa Nâo Homogêneo, o Homogêneo e o Mapa por Imagem utilizando os códigos listados na seção anterior. Abaixo está representado o crescimento de real de um fungo. | |||
<li style="display: inline-block;">[[Arquivo:Rhizomorhic-mycelium.jpg|250px|thumb|right|'''Figura 8''': Crescimento real de um micélio <ref name='REYNDERS'>B. REYNDERS. Grow mushroom cultures from spore, 2018.(https://funguys.co.za/mushroom-cultivation-tips/growing-mushrooms/grow-mushroom-cultures-from-spore/) </ref>]]</li> | |||
===Mapa Heterogêneo=== | |||
O mapa heterogêneo tem como característica principal a presença de diferentes concentrações nutricionais ao longo se sua extensão ('''figura 9''') | |||
<li style="display: inline-block;">[[Arquivo:nutri1.jpeg|250px|thumb|left|'''Figura 9''': mapa de nutrientes utilizado para obtenção da simulação 1.]]</li> | |||
<li style="display: inline-block;">[[Arquivo:mice1.jpeg|250px|thumb|right|'''Figura 10''': simulação do crescimento das hifas de um fungo após 3000 iterações.]]</li> | |||
É possível perceber através dessa imagem a nítida semelhança entre a simulação realizada utilizando o mapa não homogêneo e a a fotografia real do crescimento de um fungo mostrada anteriormente ('''figura 8'''). | |||
===Mapa Homogêneo=== | |||
Inicialmente o mapa de nutrientes homogêneo se encontra completo por nutrientes ('''figura 10'''), conforme o fungo vai crescendo parte desses nutrientes é consumida e é representada pelas partes mais claras da '''figura 11''', enquanto o fungo completamente desenvolvido está mostrado na '''figura 12'''. | |||
<li style="display: inline-block;">[[Arquivo:nutrii.jpeg|250px|thumb|center|'''Figura 10''': mapa de nutrientes inicial - e homogêneo - utilizado para obtenção da simulação 2.]]</li> | |||
<li style="display: inline-block;">[[Arquivo:nutri2.jpeg|250px|thumb|center|'''Figura 11''': mapa de nutrientes após a obtenção da simulação 2.]]</li> | |||
<li style="display: inline-block;">[[Arquivo:mice2.jpeg|250px|thumb|center|'''Figura 12''': simulação do crescimento das hifas de um fungo após 90000 iterações.]]</li> | |||
====Evolução Temporal==== | |||
Abaixo está representada a evolução temporal do crescimento de um micélio utilizando um mapa de nutrientes homogêneo como base para desenvolvimento das hifas. | |||
<li style="display: inline-block;">[[Arquivo:mice3.jpeg|1000px|thumb|center|'''Figura 13''': 5 etapas da simulação usando o mapa homogêneo de crescimento das hifas de um fungo.]]</li> | |||
Agora a mesma evolução representada com a utilização do mapa de nutrientes gerado tendo como base uma imagem. | |||
<li style="display: inline-block;">[[Arquivo:angulogrande.jpeg|1000px|thumb|center|'''Figura 14''': Evolução temporal do crescimento de hifas utilizando o mapa de imagem da '''figura 6'''.]]</li> | |||
É importante ressaltar que para cada simulação diferente, os parâmetros utilizados, para crescimento e divisão, devem ser adaptados, na figura acima, por exemplo, foi utilizado um grande desvio padrão na distribuição normal dos ângulos e por isso a figura não se formou por completo pois as hifas se interceptaram excessivamente e isso fez com que o mapa de nutrientes não fosse completamente aproveitado. | |||
===Mapa por imagem=== | |||
A possibilidade de utilizar uma imagem para realizar esse tipo de simulação é de grande importância, pois nos permite analisar um grande número de situações e formatos diversos que apresentariam grande dificuldade de serem modeladas matemáticamente como foi feita na primeira implementação. Abaixo está representada a mesma imagem da seção anterior, mas dessa vez foi diminuido o tamanho do segmento de reta do crescimento após a divisão das hifas, o que aumentou o número de divisões realizadas e consequentemente a legibilidade da frase. | |||
[[Arquivo:Muito_obrigado.png|400px|thumb|center|'''Figura 15''': simulação do crescimento do fungo utilizando o mapa de nutrientes da '''Figura 6''' (a imagem precisou ser invertida, pois os mapas advindos de imagens são invertidos).]] | |||
== Melhorias a serem realizadas == | |||
Através do trabalho realizado foi possível simular o crescimento de fungos de uma forma muito satisfatória, mas para um estudo mais aprofundado poderiam ser feitas algumas otimizações na implementação do algorítmo para deixar a simulação mais próxima da realidade, tais como: | |||
* Considerar o translocação de nutrientes realizada pelas hifas do fungo até as extremidades onde há uma escassez desses insumos; | |||
* Levar em conta a divisão lateral e não só a dicotômica; | |||
* Uma melhoria no algoritmo de detecção de intersecções entre as hifas; | |||
* Sistema de mortalidade das hifas levando em conta seu tempo de vida; | |||
* Utilizar um mapa de nutrientes contínuo e não discreto; | |||
* Permitir o movimento do fungo para que ele conseguisse "desviar" de possíveis substâncias tóxicas presentes no ambiente; | |||
* Determinar um custo nutricional para manutenção do fungo. | |||
== | == Código Completo == | ||
<source lang="python"> | <source lang="python"> | ||
import matplotlib.pyplot as plt | |||
import matplotlib.animation as animation | |||
import numpy as np | |||
import math | |||
import random | |||
from array import * | |||
import seaborn as sb | |||
global r | |||
r = 1 # tamanho de passo | |||
repeticao= 1000 # número de hifas que serão calculadas | |||
tamanho_mapa=100 # quantas divisões(quadrados) ocorrem no mapa de nutri | |||
# MAPA NUTRIENTE | |||
COORDENADA_MAPA= np.linspace(-30,30,tamanho_mapa) | |||
def divisao (x1,y1,x2,y2): | |||
x = x2 - x1 | |||
y = y2 - y1 | |||
theta= np.arctan(y/x) | theta= np.arctan(y/x) | ||
if (x<0) : | if (x<0) : | ||
theta= theta+ math.pi | theta= theta + math.pi | ||
angulodivisao= random. | angulodivisao= random.normalvariate(0, math.pi/4) | ||
angulo1= theta- angulodivisao/2 | angulo1= theta- angulodivisao/2 | ||
angulo2= theta+ angulodivisao/2 | angulo2= theta+ angulodivisao/2 | ||
addx1 = r * math.cos(angulo1) | addx1 = r * math.cos(angulo1) * 1/2 | ||
addy1 = r * math.sin(angulo1) | addy1 = r * math.sin(angulo1) * 1/2 | ||
addx2= r * math.cos(angulo2) | addx2= r * math.cos(angulo2) * 1/2 | ||
addy2= r * math.sin(angulo2) | addy2= r * math.sin(angulo2) * 1/2 | ||
Ax = | Ax = x2 + addx1 | ||
Ay = | Ay = y2 + addy1 | ||
Bx = | Bx = x2 + addx2 | ||
By= | By= y2 +addy2 | ||
return (Ax,Ay,Bx,By) | return (Ax,Ay,Bx,By) | ||
def crecimento (x1,y1,x2,y2): | |||
x = x2 - x1 | |||
y = y2 - y1 | |||
theta= np.arctan(y/x) | |||
if (x<0) : | |||
theta= theta+ math.pi | |||
aleatorio_theta = random.normalvariate(0, math.pi/4) # angulo de | |||
theta=theta+aleatorio_theta | |||
addx = r * math.cos(theta) | |||
addy = r * math.sin(theta) | |||
fx = x2 + addx | |||
fy = y2 + addy | |||
return (fx,fy) | |||
def check_anastomose(eventos,xf,yf,xi,yi): | |||
flag = True | |||
for evento in eventos: | |||
if (xi == evento[2] and yi == evento[3]): | |||
continue | |||
if (xi == evento[0] and yi == evento[1]): | |||
continue | |||
D = (evento[3]-evento[1])*(xf-xi) - (evento[2]-evento[0])*(yf-yi) | |||
uA = ((evento[2]-evento[0])*(yi-evento[1]) - (evento[3]-evento[1])*(xi-evento[0]))/D | |||
uB = ((xf-xi)*(yi-evento[1])-(yf-yi)*(xi-evento[0]))/D | |||
flag = True | |||
if (0<=uA<=1) and (0<=uB<=1): | |||
flag = False | |||
if not flag: | |||
#print("Intersection!") | |||
#print("X1:",xi," Y1:",yi, " X2:",xf," Y2:",yf) | |||
#print("X3:",evento[0]," Y3:",evento[1]," X4:",evento[2]," Y4:",evento[3]) | |||
xf, yf = get_intersection_point(uA,xf,yf,xi,yi) | |||
break | |||
return xf,yf, flag | |||
def get_intersection_point(uA,xf,yf,xi,yi): | |||
xf = xi + (uA * (xf-xi)) | |||
yf = yi + (uA * (yf-yi)) | |||
return xf,yf | |||
def find_nearest(array, value): | |||
array = np.asarray(array) | |||
idx = (np.abs(array - value)).argmin() | |||
return array[idx] | |||
def check_nutri(x,y,xmapa,ymapa,mapa_nutri): | |||
near_x = find_nearest(xmapa,x) ## encontra valor mais próximo em x | |||
near_y = find_nearest(ymapa,y) ## encontra valor mais próximo em y | |||
index_x = np.where(xmapa == near_x) ## encontra o index do valor de x | |||
index_y = np.where(ymapa == near_y) ## encontra o index do valor de y | |||
return (mapa_nutri[index_y[0][0]][index_x[0][0]]) | |||
def atualiza_mapa_nutri(x,y,xmapa,ymapa,mapa_nutri,preco): | |||
near_x = find_nearest(xmapa,x) ## encontra valor mais próximo em x | |||
near_y = find_nearest(ymapa,y) ## encontra valor mais próximo em y | |||
index_x = np.where(xmapa == near_x) ## encontra o index do valor de x | |||
index_y = np.where(ymapa == near_y) ## encontra o index do valor de y | |||
mapa_nutri[index_y[0][0]][index_x[0][0]] -= preco | |||
return (mapa_nutri) | |||
yCOORDENADA_MAPA,xCOORDENADA_MAPA = COORDENADA_MAPA,COORDENADA_MAPA | |||
def mapa_nutri_Nhomogenea(x): | |||
A,B=np.meshgrid(x,x) | |||
return (np.sin(np.sqrt(A**2+B**2))**2) | |||
def mapa_unitario_nutri(x): | |||
return (np.ones((len(x),len(x)))) | |||
# MAPA_NUTRIENTE = mapa_unitario_nutri(COORDENADA_MAPA) | |||
MAPA_NUTRIENTE = mapa_nutri_Nhomogenea(COORDENADA_MAPA) | |||
print(MAPA_NUTRIENTE) | |||
# CONDIÇÕES INICIAIS | |||
flag = True | |||
# xi yi xf yf flag | |||
eventos = np.array( [[ 0, 0, 1, 0, True]] ) | |||
for i in range (1,8): | |||
eventos = np.append( eventos, [[ 0, 0, r * math.cos(np.pi/4 *i), r * math.sin(np.pi/4*i), True]], axis=0) | |||
for i in range (0,repeticao): | |||
try: | |||
if not eventos[i][4]: | |||
continue | |||
except IndexError or Exception: | |||
break | |||
c = check_nutri(eventos[i][2],eventos[i][3],xCOORDENADA_MAPA,yCOORDENADA_MAPA,MAPA_NUTRIENTE) | |||
if (random.random() > 0.6857-0.2857*c and c>=0.3): #faz divisão | |||
custo = 0.3 | |||
c1x,c1y,c2x,c2y= divisao(eventos[i][0],eventos[i][1],eventos[i][2],eventos[i][3]) | |||
c1x,c1y,flag_1 = check_anastomose(eventos, c1x,c1y, eventos[i][2],eventos[i][3]) | |||
c2x,c2y,flag_2 = check_anastomose(eventos,c2x,c2y, eventos[i][2],eventos[i][3]) | |||
novo1 = np.array( [eventos[i][2], eventos[i][3], c1x, c1y, flag_1]) | |||
novo2 = np.array( [eventos[i][2], eventos[i][3], c2x, c2y, flag_2] ) | |||
#xf->xi yf->yi xf yf | |||
eventos = np.append( eventos, [novo1], axis=0) | |||
eventos = np.append( eventos, [novo2], axis=0) | |||
MAPA_NUTRIENTE= atualiza_mapa_nutri(eventos[i][2],eventos[i][3],xCOORDENADA_MAPA,yCOORDENADA_MAPA,MAPA_NUTRIENTE,custo) | |||
elif (c >= 0.01): #faz crescimento | |||
custo = 0.01 | |||
newx,newy = crecimento(eventos[i][0],eventos[i][1],eventos[i][2],eventos[i][3]) | |||
newx,newy,flag = check_anastomose(eventos,newx,newy,eventos[i][2],eventos[i][3]) | |||
novo = np.array( [eventos[i][2], eventos[i][3], newx, newy, flag] ) | |||
eventos = np.append( eventos, [novo], axis=0 ) | |||
MAPA_NUTRIENTE= atualiza_mapa_nutri(eventos[i][2],eventos[i][3],xCOORDENADA_MAPA,yCOORDENADA_MAPA,MAPA_NUTRIENTE,custo) | |||
plt.figure(figsize=(10,10)) | |||
plt.axes().set_facecolor("black") | |||
plt.title('Fungo com repeticoes: {}'.format(repeticao)) | |||
for j in range (0,repeticao): | |||
vet=[[eventos[j][0],eventos[j][2]],[eventos[j][1],eventos[j][3]]] | |||
plt.plot(vet[0],vet[1],color='green') | |||
</source> | |||
Plot ao longo do tempo: | |||
<source> | |||
# plot ao longo do tempo | |||
numero_plot=5 | |||
size=3 | |||
fig, axs = plt.subplots(1, numero_plot, figsize=(numero_plot*size*1.5,1*size)) | |||
repeticao=len(eventos) | |||
for j in range (0,repeticao): | |||
vet=[[eventos[j][0],eventos[j][2]],[eventos[j][1],eventos[j][3]]] | |||
axs[4].plot(vet[0],vet[1],color='green') | |||
if (j<repeticao/10): | |||
axs[0].plot(vet[0],vet[1],color='green') | |||
if (j<repeticao/4): | |||
axs[1].plot(vet[0],vet[1],color='green') | |||
if (j<repeticao/2): | |||
axs[2].plot(vet[0],vet[1],color='green') | |||
if (j<3*repeticao/4): | |||
axs[3].plot(vet[0],vet[1],color='green') | |||
axs[0].set_title("{}".format(int(repeticao/10))) | |||
axs[1].set_title("{}".format(int(repeticao/4))) | |||
axs[2].set_title("{}".format(int(repeticao/2))) | |||
axs[3].set_title("{}".format(int(3*repeticao/4))) | |||
axs[4].set_title("{}".format(int(repeticao))) | |||
axis=80 | |||
for b in range (0,numero_plot): | |||
axs[b].set_xlim(-45,70) | |||
axs[b].set_ylim(-45,80) | |||
fig.suptitle('Fungo com repeticoes: {}\n'.format(repeticao)) | |||
plt.show() | |||
</source> | </source> | ||
== Referências == | == Referências == | ||
<references/> | |||
Edição atual tal como às 00h27min de 26 de maio de 2021
Grupo: Arthur Dornelles, Bruno Zanette, Gabriel De David e Guilherme Hoss
O objetivo deste trabalho é modelar computacionalmente o desenvolvimento de micélios em fungos com base em mecanismos gerais pré-estabelecidos buscando a criação de estruturas similares com micélios reais. O progresso e a complexidade dos modelos cresceram de maneira gradual ao longo do trabalho através de diferentes modelos de crescimento. O trabalho foi inspirado - principalmente - nos dois primeiros capítulos do artigo de Steven Hopkins [1].
Motivação e Introdução aos Fungos
Fungos estão integrados em grande parte dos ecossistemas do planeta e cumprem importantes funções na manutenção e sobrevivência dos mesmos. De maneira geral, eles produzem enzimas que são responsáveis pela decomposição de matéria orgânica e - portanto - a reciclagem de diversos nutrientes do ambiente ao seu redor [3]. Em muitos casos, fungos formam fusões simbióticas com plantas ou algas e interagem de diferentes maneiras com diferentes organismos vivos. Neste trabalho, todavia, não faremos a análise dessas interações e focaremos no comportamento individual de crescimento de fungos.
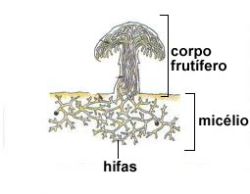
Anatomicamente, fungos são compostos por células que se assemelham a tubos microscópicos, denominadas de hifas. Essas hifas então se ramificam e se fundem umas com as outras em um processo chamado de anastomose, formando uma complexa rede chamada de micélio (figura 1).
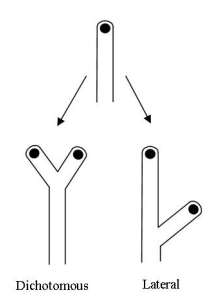
A criação de novas hifas, em geral, ocorre ao longo do tempo através de dois processos principais: o primeiro, denominado de ramificação dicotômica, consiste na ponta de uma hifa já existente se dividindo ao meio. O segundo processo é chamado de ramificação lateral, no qual, como o nome sugere, formam-se novos ramos e hifas na lateral de uma hifa já existente, como pode ser visto na figura 2.
Tendo em vista o objetivo deste trabalho, é importante também entender o porquê e quando as ramificações citadas acimas ocorrem, para que possamos programá-las em nosso modelo computacional. A ramificação, portanto, é atribuída ao acúmulo de partículas de nutrientes e materiais no ambiente, o que estimula a extensão das hifas dos fungos em sua direção. Dessa maneira, o crescimento e desenvolvimento dos fungos são altamente dependentes e influenciados pela disponibilidade de nutrientes e materiais no ambiente ao seu redor. Apesar desse fato, fungos podem continuar se desenvolvendo até em ambientes com poucos nutrientes, devido ao processo de translocação, no qual os nutrientes previamente absorvidos pelo fungo podem ser transportados internamente, bancando o crescimento do mesmo em locais com deficiência de nutrientes [1].
Mecanismos Gerais dos Modelos
Um dos grandes obstáculos com a programação de um modelo biológico com variáveis discretas é o processamento de grandes quantidades de dados. Conforme o tempo de simulação aumenta e as redes de hifas se tornam maiores e mais complexas, a quantidade de informação processada aumenta exponencialmente e, devido a esse fato, algumas características típicas do desenvolvimento de fungos citadas na primeira seção foram deixadas de lado para a construção de nosso modelo computacional (como a ramificação lateral e a translocação). No entanto, os mecanismos essenciais para o bom funcionamento da simulação foram mantidos e serão abordados mais profundamente nessa seção.
Crescimento
Fungos possuem - nas pontas de suas hifas - uma estrutura chamada de Spitzenkörper (corpo superior em alemão). Essa estrutura possui a função de orientar a hifa em seu crescimento e de transformar todo o material de crescimento (nutriente) encontrado em material para as paredes de seus tubos, o que leva à expansão de tamanho do fungo [4]. Por isso, tipicamente, as hifas dos fungos crescem de maneira apical (em suas pontas) e em linha reta, possuindo baixa variação em sua orientação e, quando há variação, as mudanças no ângulo de crescimento ocorrem devido a um deslocamento do Spitzenkörper. Estudos anteriores demonstram que essas variações na angulação são - para certas espécies - normalmente distribuídas [5]. A espécie Mucor hiemalis, por exemplo, possui uma angulação média de 56° e desvio padrão de 17° [6]. Como comentado anteriormente, a concentração de substrato (nutrientes) presente no local da ponta da hifa irá determinar se a expansão da mesma irá ocorrer ou não. Por isso, computacionalmente, a extensão das hifas é modelada de maneira que a concentração de nutrientes na ponta de um hifa arbitrária é checada e, caso haja substrato o suficiente (é determinado um limiar de acordo com a espécie de fungo), o crescimento da hifa segue adiante, caso contrário ele permanece estagnado. Além disso, a orientação do ângulo de crescimento é dependente da orientação inicial da hifa e de um fator aleatório dependente da espécie a ser analisada.

Divisão e Anastomose
Os dois tipos de divisões - ou ramificações - citadas anteriormente na seção introdutória variam entre as diferentes espécies de fungo e - da mesma maneira que o crescimento por expansão das hifas - são altamente dependentes da alta concentração de nutrientes em seu ambiente. Além disso, a absorção de novos nutrientes através do Spitzenkörper resulta em uma pressão de Turgor (ou pressão hidrostática) nas paredes internas do fungo, o que também influencia diretamente no processo de ramificação das hifas [1]. Conforme o crescimento do fungo ocorre e suas ramificações acontecem, o processo de encontro e fusão das pontas das hifas dos fungos citado na primeira seção (anastomose) começa a ocorrer. Este processo também pode ocorrer de diferentes maneiras, como pode ser visto na figura 3. Após a ocorrência de ambos os processos, as hifas - agora juntas umas das outras - passam a permitir a transmissão de substâncias internamente entre si. Computacionalmente e de maneira similar ao crescimento, as divisões também dependem da quantidade de nutrientes presentes no local de possível ramificação e - além disso - dependem de um fator de ângulo aleatório que varia com a espécie simulada. A anastomose, por outro lado, possui uma programação mais complexa e utiliza o método de intersecção de linhas, que será mais aprofundado na próxima seção.
Formulação Matemática e Implementação
O código base que chama as funções é o seguinte:
flag = True
# xi yi xf yf flag
eventos = np.array( [[ 0, 0, 1, 0, True]] )
for i in range (1,8):
eventos = np.append( eventos, [[ 0, 0, r * math.cos(np.pi/4 *i), r * math.sin(np.pi/4*i), True]], axis=0)
for i in range (0,repeticao):
try:
if not eventos[i][4]:
continue
except IndexError or Exception:
break
c = check_nutri(eventos[i][2],eventos[i][3],xCOORDENADA_MAPA,yCOORDENADA_MAPA,MAPA_NUTRIENTE)
if (random.random() > 0.6857-0.2857*c and c>=0.3): #faz divisão
custo = 0.3
c1x,c1y,c2x,c2y= divisao(eventos[i][0],eventos[i][1],eventos[i][2],eventos[i][3])
c1x,c1y,flag_1 = check_anastomose(eventos, c1x,c1y, eventos[i][2],eventos[i][3])
c2x,c2y,flag_2 = check_anastomose(eventos,c2x,c2y, eventos[i][2],eventos[i][3])
novo1 = np.array( [eventos[i][2], eventos[i][3], c1x, c1y, flag_1])
novo2 = np.array( [eventos[i][2], eventos[i][3], c2x, c2y, flag_2] )
#xf->xi yf->yi xf yf
eventos = np.append( eventos, [novo1], axis=0)
eventos = np.append( eventos, [novo2], axis=0)
MAPA_NUTRIENTE= atualiza_mapa_nutri(eventos[i][2],eventos[i][3],xCOORDENADA_MAPA,yCOORDENADA_MAPA,MAPA_NUTRIENTE,custo)
elif (c >= 0.01): #faz crescimento
custo = 0.01
newx,newy = crecimento(eventos[i][0],eventos[i][1],eventos[i][2],eventos[i][3])
newx,newy,flag = check_anastomose(eventos,newx,newy,eventos[i][2],eventos[i][3])
novo = np.array( [eventos[i][2], eventos[i][3], newx, newy, flag] )
eventos = np.append( eventos, [novo], axis=0 )
MAPA_NUTRIENTE= atualiza_mapa_nutri(eventos[i][2],eventos[i][3],xCOORDENADA_MAPA,yCOORDENADA_MAPA,MAPA_NUTRIENTE,custo)
Os principais mecanismos são: eventos que armazena os segmentos de retas com xi yi xf yf flag; flag representa se ocorreu o processo de anastomose, caso flag armazene False o primeiro try faz o segmento parar de crescer; Dentro do for principal há um if e else que junto da condição random.random() > 0.6857-0.2857*c faz com que 60% de chance de ocorrer de divisão quando c é igual a 1, pois random.random() é um valor entre [0,1].
Utilizando as informações biológicas apresentadas nas seções anteriores, é possível criar funções matemáticas e computacionais para a programação dos aspectos fundamentais de uma simulação de micélio de fungos.
- Funções:
O Crescimento e divisão dependem do ângulo do segmento originário, uma forma de consegui-lo é através da equação:
É importante lembrar que para x negativos deve-se somar . Esse cálculo, nas duas funções, implementa-se assim:
x = x2 - x1
y = y2 - y1
theta= np.arctan(y/x)
if (x<0) :
theta= theta+ math.pi
aleatorio_theta = random.normalvariate(0, math.pi/4) # angulo de
theta=theta+aleatorio_theta
Crescimento
Soma-se este ângulo com um número aleatório normalmente distribuído com média zero e sigma dependente de dados estatísticos advindos da observação do fungo que pretende-se modelar. Agora com o ângulo modificado podemos adquirir um x e y final para o novo segmento com e respectivamente, onde r é uma variável global que representa o tamanho de cada hifa.
def crecimento (x1,y1,x2,y2):
x = x2 - x1
y = y2 - y1
theta= np.arctan(y/x)
if (x<0) :
theta= theta+ math.pi
aleatorio_theta = random.normalvariate(0, math.pi/4) # angulo de
theta=theta+aleatorio_theta
addx = r * math.cos(theta)
addy = r * math.sin(theta)
fx = x2 + addx
fy = y2 + addy
return (fx,fy)
Divisão
A divisão trabalha com uma ideia similar ao crescimento, porém o ângulo aleatório normalmente distribuído é o ângulo que separa as duas hifas criadas
def divisao (x1,y1,x2,y2):
x = x2 - x1
y = y2 - y1
theta= np.arctan(y/x)
if (x<0) :
theta= theta + math.pi
angulodivisao= random.normalvariate(0, math.pi/4)
angulo1= theta- angulodivisao/2
angulo2= theta+ angulodivisao/2
addx1 = r * math.cos(angulo1)
addy1 = r * math.sin(angulo1)
addx2= r * math.cos(angulo2)
addy2= r * math.sin(angulo2)
Ax = x2 + addx1
Ay = y2 + addy1
Bx = x2 + addx2
By= y2 +addy2
return (Ax,Ay,Bx,By)
Intersecção de Linhas e Anastomose
A cada novo crescimento ou divisão, devemos verificar se há cruzamento entre algumas das linhas. Uma forma de tornar o código mais eficiente seria um algorítimo de detecção de cruzamentos que desconsiderasse alguns segmentos que estão muito longe na hora de calcular.
A interseção de duas linhas e pode ser definida utilizando determinantes dados dois pontos em cada linha. Portanto, podemos descobrir se a linha definida por dois pontos distintos e , e a linha definida por dois pontos distintos e se intersectam calculando as seguintes equações matriciais:[7]
Trata-se as linhas como uma curva de Bézier de primeiro grau:
Onde e são números reais definidos como:
E o ponto de intersecção:
O ponto de interseção cai dentro do segmento da primeira linha se , e cai dentro do segmento da segunda linha se . [8]
def check_anastomose(eventos,xf,yf,xi,yi):
flag = True
for evento in eventos:
if (xi == evento[2] and yi == evento[3]):
continue
if (xi == evento[0] and yi == evento[1]):
continue
D = (evento[3]-evento[1])*(xf-xi) - (evento[2]-evento[0])*(yf-yi)
uA = ((evento[2]-evento[0])*(yi-evento[1]) - (evento[3]-evento[1])*(xi-evento[0]))/D
uB = ((xf-xi)*(yi-evento[1])-(yf-yi)*(xi-evento[0]))/D
flag = True
if (0<=uA<=1) and (0<=uB<=1):
flag = False
if not flag:
xf, yf = get_intersection_point(uA,xf,yf,xi,yi)
break
return xf,yf, flag
Os primeiros dois ifs identifica se a hifa a qual essa foi originada é quem está sendo calculada. Se não há cruzamento temos que flag = False, o que significa que a hifa pode continuar crescendo, caso haja ponto de intersecção é chamada a get_intersection_point para encontrar o ponto:
def get_intersection_point(uA,xf,yf,xi,yi):
xf = xi + (uA * (xf-xi))
yf = yi + (uA * (yf-yi))
return xf,yf
Mapa de Nutrientes
Um mapa de nutriente (Figura 4) é definido como uma matriz que armazena o valor de nutriente em cada ponto identificado pela matriz X e Y, o mapa de nutrientes implementado foi um mapa discreto, ao contrário do artigo [1] que implementou um mapa contínuo.
Logo, é necessário encontrar em qual "quadrado" de nutriente a posição do final da hifa está. Para isto usa-se uma função (find_nearest) que encontra o valor mais próximo de x e y no array que representa o mapa de nutriente:
def find_nearest(array, value):
array = np.asarray(array)
idx = (np.abs(array - value)).argmin()
return array[idx]
Portanto, a função check_nutri que retorna a quantidade de nutrientes disponível utiliza a find_nearest para encontrar o index do ponto que é também o do nutriente no ponto na matriz mapa_nutri:
def check_nutri(x,y,xmapa,ymapa,mapa_nutri):
near_x = find_nearest(xmapa,x) ## encontra valor mais próximo em x
near_y = find_nearest(ymapa,y) ## encontra valor mais próximo em y
index_x = np.where(xmapa == near_x) ## encontra o index do valor de x
index_y = np.where(ymapa == near_y) ## encontra o index do valor de y
return (mapa_nutri[index_y[0][0]][index_x[0][0]])
A função atualiza_mapa_nutri funciona de maneira similar a check_nutri porém essa recebe recebe também a variável preco que representa o custo de uma ação. Para nossa situação as únicas situações que custam nutrientes são o crescimento e a divisão, 0.01 e 0.3 respectivamente. A função então retorna o mapa de nutriente atualizado:
def atualiza_mapa_nutri(x,y,xmapa,ymapa,mapa_nutri,preco):
near_x = find_nearest(xmapa,x) ## encontra valor mais próximo em x
near_y = find_nearest(ymapa,y) ## encontra valor mais próximo em y
index_x = np.where(xmapa == near_x) ## encontra o index do valor de x
index_y = np.where(ymapa == near_y) ## encontra o index do valor de y
mapa_nutri[index_y[0][0]][index_x[0][0]] -= preco
return (mapa_nutri)
Criação do mapa
Implementamos três formas de criar o mapa. A função mapa_nutri_Nhomogenea cria um mapa dependente de uma função que necessariamente deve começar a partir de 0, no caso da função mostrada é , ela recebe só uma variável para montar um mapa quadrado - com os mesmos números horizontal e verticalmente - e produz o mapa mostrado na Figura 9
def mapa_nutri_Nhomogenea(x):
A,B=np.meshgrid(x,x)
return (np.sin(np.sqrt(A**2+B**2))**2)
A função mapa_unitario_nutri cria um mapa homogêneo com todos os nutrientes começando em 1. Exemplo após crescimento do fungo mostrado na Figura 13
def mapa_unitario_nutri(x):
return (np.ones((len(x),len(x))))
A terceira forma é utilizando uma imagem, como a da Figura 5, que transforma o gradiente de preto a branco dos pontos (x_mapa,y_mapa) em um mapa de nutriente, mostrado Figura 6, Preto representa 0 nutriente e branco 1.
import cv2
import numpy as np
import sys
import seaborn as sn
img_path = '/content/OBRIGADO.png'
img = cv2.imread(img_path, 0) # read image as grayscale. Set second parameter to 1 if rgb is required
img_reverted= cv2.bitwise_not(img)
new_img = img_reverted / 255.0 # now all values are ranging from 0 to 1, where white equlas 0.0 and black equals 1.0
for i in range (0,len(new_img)):
for j in range (0,len(new_img[0])):
new_img[i][j]=-(new_img[i][j]-1)
x_mapa = np.linspace(-80,80,int(len(new_img[0])/1))
y_mapa = np.linspace(-80,80,int(len(new_img)/1))
np.set_printoptions(threshold=sys.maxsize)
sn.heatmap(new_img)
xCOORDENADA_MAPA= x_mapa
yCOORDENADA_MAPA= y_mapa
MAPA_NUTRIENTE = new_img
Condições Iniciais
As condições iniciais em formato de estrela são mostradas na Figura 7 e implementadas assim:
eventos = np.array( [[ 0, 0, 1, 0, True]] ) # xi yi xf yf flag
for i in range (1,8):
eventos = np.append( eventos, [[ 0, 0, r * math.cos(np.pi/4 *i), r * math.sin(np.pi/4*i), True]], axis=0)
Discussão de Resultados
Como discutido anteriormente o mapa de nutrientes utilizado nas simulações de crescimento das hifas interfere diretamente no resultado final referente ao formato do micélio gerado. Para exemplificar essa diferença executamos 3 simulações utilizando cada um dos três estilos de mapas mostrados já citados, o Mapa Nâo Homogêneo, o Homogêneo e o Mapa por Imagem utilizando os códigos listados na seção anterior. Abaixo está representado o crescimento de real de um fungo.

Mapa Heterogêneo
O mapa heterogêneo tem como característica principal a presença de diferentes concentrações nutricionais ao longo se sua extensão (figura 9)
É possível perceber através dessa imagem a nítida semelhança entre a simulação realizada utilizando o mapa não homogêneo e a a fotografia real do crescimento de um fungo mostrada anteriormente (figura 8).
Mapa Homogêneo
Inicialmente o mapa de nutrientes homogêneo se encontra completo por nutrientes (figura 10), conforme o fungo vai crescendo parte desses nutrientes é consumida e é representada pelas partes mais claras da figura 11, enquanto o fungo completamente desenvolvido está mostrado na figura 12.
Evolução Temporal
Abaixo está representada a evolução temporal do crescimento de um micélio utilizando um mapa de nutrientes homogêneo como base para desenvolvimento das hifas.
Agora a mesma evolução representada com a utilização do mapa de nutrientes gerado tendo como base uma imagem.
É importante ressaltar que para cada simulação diferente, os parâmetros utilizados, para crescimento e divisão, devem ser adaptados, na figura acima, por exemplo, foi utilizado um grande desvio padrão na distribuição normal dos ângulos e por isso a figura não se formou por completo pois as hifas se interceptaram excessivamente e isso fez com que o mapa de nutrientes não fosse completamente aproveitado.
Mapa por imagem
A possibilidade de utilizar uma imagem para realizar esse tipo de simulação é de grande importância, pois nos permite analisar um grande número de situações e formatos diversos que apresentariam grande dificuldade de serem modeladas matemáticamente como foi feita na primeira implementação. Abaixo está representada a mesma imagem da seção anterior, mas dessa vez foi diminuido o tamanho do segmento de reta do crescimento após a divisão das hifas, o que aumentou o número de divisões realizadas e consequentemente a legibilidade da frase.
Melhorias a serem realizadas
Através do trabalho realizado foi possível simular o crescimento de fungos de uma forma muito satisfatória, mas para um estudo mais aprofundado poderiam ser feitas algumas otimizações na implementação do algorítmo para deixar a simulação mais próxima da realidade, tais como:
- Considerar o translocação de nutrientes realizada pelas hifas do fungo até as extremidades onde há uma escassez desses insumos;
- Levar em conta a divisão lateral e não só a dicotômica;
- Uma melhoria no algoritmo de detecção de intersecções entre as hifas;
- Sistema de mortalidade das hifas levando em conta seu tempo de vida;
- Utilizar um mapa de nutrientes contínuo e não discreto;
- Permitir o movimento do fungo para que ele conseguisse "desviar" de possíveis substâncias tóxicas presentes no ambiente;
- Determinar um custo nutricional para manutenção do fungo.
Código Completo
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np
import math
import random
from array import *
import seaborn as sb
global r
r = 1 # tamanho de passo
repeticao= 1000 # número de hifas que serão calculadas
tamanho_mapa=100 # quantas divisões(quadrados) ocorrem no mapa de nutri
# MAPA NUTRIENTE
COORDENADA_MAPA= np.linspace(-30,30,tamanho_mapa)
def divisao (x1,y1,x2,y2):
x = x2 - x1
y = y2 - y1
theta= np.arctan(y/x)
if (x<0) :
theta= theta + math.pi
angulodivisao= random.normalvariate(0, math.pi/4)
angulo1= theta- angulodivisao/2
angulo2= theta+ angulodivisao/2
addx1 = r * math.cos(angulo1) * 1/2
addy1 = r * math.sin(angulo1) * 1/2
addx2= r * math.cos(angulo2) * 1/2
addy2= r * math.sin(angulo2) * 1/2
Ax = x2 + addx1
Ay = y2 + addy1
Bx = x2 + addx2
By= y2 +addy2
return (Ax,Ay,Bx,By)
def crecimento (x1,y1,x2,y2):
x = x2 - x1
y = y2 - y1
theta= np.arctan(y/x)
if (x<0) :
theta= theta+ math.pi
aleatorio_theta = random.normalvariate(0, math.pi/4) # angulo de
theta=theta+aleatorio_theta
addx = r * math.cos(theta)
addy = r * math.sin(theta)
fx = x2 + addx
fy = y2 + addy
return (fx,fy)
def check_anastomose(eventos,xf,yf,xi,yi):
flag = True
for evento in eventos:
if (xi == evento[2] and yi == evento[3]):
continue
if (xi == evento[0] and yi == evento[1]):
continue
D = (evento[3]-evento[1])*(xf-xi) - (evento[2]-evento[0])*(yf-yi)
uA = ((evento[2]-evento[0])*(yi-evento[1]) - (evento[3]-evento[1])*(xi-evento[0]))/D
uB = ((xf-xi)*(yi-evento[1])-(yf-yi)*(xi-evento[0]))/D
flag = True
if (0<=uA<=1) and (0<=uB<=1):
flag = False
if not flag:
#print("Intersection!")
#print("X1:",xi," Y1:",yi, " X2:",xf," Y2:",yf)
#print("X3:",evento[0]," Y3:",evento[1]," X4:",evento[2]," Y4:",evento[3])
xf, yf = get_intersection_point(uA,xf,yf,xi,yi)
break
return xf,yf, flag
def get_intersection_point(uA,xf,yf,xi,yi):
xf = xi + (uA * (xf-xi))
yf = yi + (uA * (yf-yi))
return xf,yf
def find_nearest(array, value):
array = np.asarray(array)
idx = (np.abs(array - value)).argmin()
return array[idx]
def check_nutri(x,y,xmapa,ymapa,mapa_nutri):
near_x = find_nearest(xmapa,x) ## encontra valor mais próximo em x
near_y = find_nearest(ymapa,y) ## encontra valor mais próximo em y
index_x = np.where(xmapa == near_x) ## encontra o index do valor de x
index_y = np.where(ymapa == near_y) ## encontra o index do valor de y
return (mapa_nutri[index_y[0][0]][index_x[0][0]])
def atualiza_mapa_nutri(x,y,xmapa,ymapa,mapa_nutri,preco):
near_x = find_nearest(xmapa,x) ## encontra valor mais próximo em x
near_y = find_nearest(ymapa,y) ## encontra valor mais próximo em y
index_x = np.where(xmapa == near_x) ## encontra o index do valor de x
index_y = np.where(ymapa == near_y) ## encontra o index do valor de y
mapa_nutri[index_y[0][0]][index_x[0][0]] -= preco
return (mapa_nutri)
yCOORDENADA_MAPA,xCOORDENADA_MAPA = COORDENADA_MAPA,COORDENADA_MAPA
def mapa_nutri_Nhomogenea(x):
A,B=np.meshgrid(x,x)
return (np.sin(np.sqrt(A**2+B**2))**2)
def mapa_unitario_nutri(x):
return (np.ones((len(x),len(x))))
# MAPA_NUTRIENTE = mapa_unitario_nutri(COORDENADA_MAPA)
MAPA_NUTRIENTE = mapa_nutri_Nhomogenea(COORDENADA_MAPA)
print(MAPA_NUTRIENTE)
# CONDIÇÕES INICIAIS
flag = True
# xi yi xf yf flag
eventos = np.array( [[ 0, 0, 1, 0, True]] )
for i in range (1,8):
eventos = np.append( eventos, [[ 0, 0, r * math.cos(np.pi/4 *i), r * math.sin(np.pi/4*i), True]], axis=0)
for i in range (0,repeticao):
try:
if not eventos[i][4]:
continue
except IndexError or Exception:
break
c = check_nutri(eventos[i][2],eventos[i][3],xCOORDENADA_MAPA,yCOORDENADA_MAPA,MAPA_NUTRIENTE)
if (random.random() > 0.6857-0.2857*c and c>=0.3): #faz divisão
custo = 0.3
c1x,c1y,c2x,c2y= divisao(eventos[i][0],eventos[i][1],eventos[i][2],eventos[i][3])
c1x,c1y,flag_1 = check_anastomose(eventos, c1x,c1y, eventos[i][2],eventos[i][3])
c2x,c2y,flag_2 = check_anastomose(eventos,c2x,c2y, eventos[i][2],eventos[i][3])
novo1 = np.array( [eventos[i][2], eventos[i][3], c1x, c1y, flag_1])
novo2 = np.array( [eventos[i][2], eventos[i][3], c2x, c2y, flag_2] )
#xf->xi yf->yi xf yf
eventos = np.append( eventos, [novo1], axis=0)
eventos = np.append( eventos, [novo2], axis=0)
MAPA_NUTRIENTE= atualiza_mapa_nutri(eventos[i][2],eventos[i][3],xCOORDENADA_MAPA,yCOORDENADA_MAPA,MAPA_NUTRIENTE,custo)
elif (c >= 0.01): #faz crescimento
custo = 0.01
newx,newy = crecimento(eventos[i][0],eventos[i][1],eventos[i][2],eventos[i][3])
newx,newy,flag = check_anastomose(eventos,newx,newy,eventos[i][2],eventos[i][3])
novo = np.array( [eventos[i][2], eventos[i][3], newx, newy, flag] )
eventos = np.append( eventos, [novo], axis=0 )
MAPA_NUTRIENTE= atualiza_mapa_nutri(eventos[i][2],eventos[i][3],xCOORDENADA_MAPA,yCOORDENADA_MAPA,MAPA_NUTRIENTE,custo)
plt.figure(figsize=(10,10))
plt.axes().set_facecolor("black")
plt.title('Fungo com repeticoes: {}'.format(repeticao))
for j in range (0,repeticao):
vet=[[eventos[j][0],eventos[j][2]],[eventos[j][1],eventos[j][3]]]
plt.plot(vet[0],vet[1],color='green')
Plot ao longo do tempo:
# plot ao longo do tempo
numero_plot=5
size=3
fig, axs = plt.subplots(1, numero_plot, figsize=(numero_plot*size*1.5,1*size))
repeticao=len(eventos)
for j in range (0,repeticao):
vet=[[eventos[j][0],eventos[j][2]],[eventos[j][1],eventos[j][3]]]
axs[4].plot(vet[0],vet[1],color='green')
if (j<repeticao/10):
axs[0].plot(vet[0],vet[1],color='green')
if (j<repeticao/4):
axs[1].plot(vet[0],vet[1],color='green')
if (j<repeticao/2):
axs[2].plot(vet[0],vet[1],color='green')
if (j<3*repeticao/4):
axs[3].plot(vet[0],vet[1],color='green')
axs[0].set_title("{}".format(int(repeticao/10)))
axs[1].set_title("{}".format(int(repeticao/4)))
axs[2].set_title("{}".format(int(repeticao/2)))
axs[3].set_title("{}".format(int(3*repeticao/4)))
axs[4].set_title("{}".format(int(repeticao)))
axis=80
for b in range (0,numero_plot):
axs[b].set_xlim(-45,70)
axs[b].set_ylim(-45,80)
fig.suptitle('Fungo com repeticoes: {}\n'.format(repeticao))
plt.show()Referências
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 S. Hopkins. A Hybrid Mathematical Model of Fungal Mycelia: Tropisms, Polarised Growth and Application to Colony Competition, tese de doutorado, 2011.(https://core.ac.uk/download/pdf/6117416.pdf)
- ↑ P. L. Moraes. Fungos. Mundo Educação. Disponível em: https://mundoeducacao.uol.com.br/biologia/os-fungos.htm. Acesso em: 15 de Maio de 2021.
- ↑ P. da Silva. Reino Fungi. Info Escola (2018). Disponível em: https://www.infoescola.com/biologia/reino-fungi. Acesso em: 15 de Maio de 2021.
- ↑ G. Steinberg (2007). "Hyphal growth: a tale of motors, lipids, and the Spitzenkörper". Eukaryotic Cell. 6 (3): 351–360. doi:10.1128/EC.00381-06
- ↑ Molin, P., P. Gervais, J. Lemiere, and T. Davet (1992). Direction of hyphal growth: a relevant parameter in the development of filamentous fungi. Research in Microbiology 143, 777–784. doi: 10.1016/0923-2508(92)90106-x.
- ↑ Hutchinson, S. A., P. Sharma, K. R. Clarke, and I. Macdonald (1980). Control of hyphal orientation in colonies of Mucor hiemalis. Transactions of the British Mycological Society 75, 177–191. doi: 10.1016/S0007-1536(80)80078-7
- ↑ Weisstein, Eric W. "Line-Line Intersection." From MathWorld Disponível em: http://mathworld.wolfram.com/Line-LineIntersection.html
- ↑ Line to line intersection. Wikipedia, the free encyclopedia. Disponível em: https://en.wikipedia.org/wiki/Line%E2%80%93line_intersection. Acesso em: 20 de Maio de 2021.
- ↑ B. REYNDERS. Grow mushroom cultures from spore, 2018.(https://funguys.co.za/mushroom-cultivation-tips/growing-mushrooms/grow-mushroom-cultures-from-spore/)




















![{\displaystyle MN=\left[{\begin{matrix}0.99977783&0.97620649&0.99977783\\0.97620649&0&0.97620649\\0.99977783&0.97620649&0.99977783\end{matrix}}\right]\quad X=Y=[{\begin{matrix}-30&0&30\end{matrix}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bed6edd8a9141b256e34ad41972196fecb1a6bc)