Modelo de Potts 2D: mudanças entre as edições
Sem resumo de edição |
|||
| (115 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
== Modelo de Potts == | == Modelo de Potts == | ||
=== O Modelo === | |||
O "modelo de Potts de Q-estados" trata de um sistema de rede com N spins interagentes <math>s=\{s_1,s_2,..s_i,...s_N\}</math>, onde um spin <math>s_i</math> pode assumir valores discretos <math>q \in{\{0, 1, 2, ..., Q-2, Q, Q-1\}}</math>. Cada spin do sistema está limitado a interagir com outros spins em sua vizinhança e a energia da interação entre dois spins <math>s_i</math> e <math>s_j</math> é dada pelo potencial | O "modelo de Potts de Q-estados" trata de um sistema de rede com N spins interagentes <math>s=\{s_1,s_2,..s_i,...s_N\}</math>, onde um spin <math>s_i</math> pode assumir valores discretos <math>q \in{\{0, 1, 2, ..., Q-2, Q, Q-1\}}</math>. Cada spin do sistema está limitado a interagir com outros spins em sua vizinhança e a energia da interação entre dois spins <math>s_i</math> e <math>s_j</math> é dada pelo potencial | ||
| Linha 11: | Linha 12: | ||
Este modelo é tido como uma generalização natural do [https://fiscomp.if.ufrgs.br/index.php/Ising_2D Modelo de Ising] e para o caso <math>Q = 2</math> ambos modelos são equivalentes a menos de uma constante: | Este modelo é tido como uma generalização natural do [https://fiscomp.if.ufrgs.br/index.php/Ising_2D Modelo de Ising] e para o caso <math>Q = 2</math> ambos modelos são equivalentes a menos de uma constante: | ||
<math>\mathcal{H}_{ising} = \mathcal{H}_{potts} + \sum_{\langle i,j \rangle}\frac{J}{2} = -\frac{J}{2}\sum_{\langle i,j \rangle} | <math>\mathcal{H}_{ising} = \mathcal{H}_{potts} + \sum_{\langle i,j \rangle}\frac{J}{2} = -\frac{J}{2}\sum_{\langle i,j \rangle}[2\delta(s_i,s_j) - 1] </math> | ||
Nesse caso, a interação entre dois spins <math>s_i</math> e <math>s_j</math> assume a mesma dinâmica do modelo de Ising a contribuição para a energia do sistema será | Nesse caso, a interação entre dois spins <math>s_i</math> e <math>s_j</math> assume a mesma dinâmica do modelo de Ising a contribuição para a energia do sistema será | ||
<math> V(s_i,s_j) = \begin{cases} | <math> V(s_i,s_j) = \begin{cases} | ||
-\frac{J}{2}, \ | -\frac{J}{2}, \qquad \text{se } s_i = s_j \\ | ||
\frac{J}{2}, \qquad \text{se } s_i \neq s_j | |||
\end{cases}</math> | \end{cases}</math> | ||
Neste trabalho o modelo de Potts foi estudado em uma rede quadrada 2D com vizinhança de von Neumann para primeiros vizinhos. A quantidade de spins no modelo é <math>N = L\times L</math> com interações ferromagnéticas com <math>J = 1</math>. | === Motivações === | ||
Por muitos anos o modelo de Potts foi considerado um sistema que exibe transição de ordem e desordem de interesse apenas teórico, mas atualmente se sabe que as propriedades do modelo de Potts podem ser encontradas em sistemas reais e podem ser medidos através da realização de experimentos. | |||
O princípio básico na experimentação de sistemas de spin é o princípio da universalidade, onde busca-se identificar sistemas reais que pertencem a mesma classe de universalidade do modelo de spin em questão. Ou seja, medindo os expoentes críticos do experimento, encontramos sua classe. | |||
Para <math> Q = 2 </math> sabemos que o modelo de Potts possui as propriedades do modelo de Ising. Em duas dimensões, foi provado <ref name = WU>F. Y. Wu, The Potts Model, Rev. Mod. Phys. 54, 235, 1982</ref> que um sistema absorvido de átomos de <math>He^{4}</math> cobrindo <math>\frac{1}{2}</math> de uma rede honeycomb de grafite exibe o mesmo expoente crítico do calor específico que o modelo de Ising. Esse mesmo sistema, mas agora cobrindo <math>\frac{1}{3}</math> da rede exibe o comportamento do modelo de Potts para <math> Q = 3 </math>. Outros estudos de sistemas absorvidos, como <math>N_{2}</math> em uma rede 2D de grafite, mostram mostram comportamento da classe <math>Q = 4</math>. Também foi provado que polímeros que interagem em soluções, como processos de vulcanização <ref name = WU></ref> de polímeros ramificados tem a classe de universalidade para o modelo de Potts com <math> 0 \leq Q \leq 1</math>. Uma breve observação: o modelo de Potts de <math>q</math>-estados generalizado não exige que <math>q</math> seja um valor inteiro, mas neste trabalho só tratamos desse caso. | |||
=== Modelo celular de Potts === | |||
Além da física de materiais, o modelo de Potts também é aplicado em biologia computacional para a simulação de células através do modelo celular de Potts. Esse modelo trata células como objetos deformáveis que podem mover, crescer ou até se dividir e pode simular o comportamento coletivo de células, estudando o surgimento de células cancerígenas e morfogênese. | |||
A energia do sistema é descrita por | |||
<math> | |||
\mathcal{H} = -\sum_{\langle i,j \rangle}J_{\sigma_i,\sigma_j}\left(1-\delta_{\sigma_i,\sigma_j}\right) + \lambda\sum_{\sigma_i}\left(v(\sigma_i)-V(\sigma_i)\right)^2 | |||
</math> | |||
onde <math>i</math>, <math>j</math> são posições da rede, <math>\sigma_{i}</math> é a célula na posição <math>i</math>, <math>J</math> é o coeficiente determinando a adesão de dois tipos diferentes de células, <math>v(\sigma)</math> é o volume da célula <math>\sigma</math>, <math>V(\sigma)</math> é o volume padrão de <math>\sigma</math> e <math>\lambda</math> determina a força da elasticidade volumétrica da célula. O modelo pode considerar ainda elasticidade de área e perímetro de cada célula. | |||
== Método de Monte Carlo == | |||
O método de Monte Carlo é aplicado ao modelo de Potts com o objetivo de gerar estados de equilíbrio para medir os observáveis do sistema. Os <math>N</math> spins são iniciados com valores aleatórios de Q na rede e o método de Monte Carlo escolhe arbitrariamente um spin <math>s_i</math> e gera um novo valor de <math>q\in Q | q \neq s_i</math> para o spin. A partir disso, através de algum algoritmo específico, se escolhe como os estados serão gerados e quais serão aceitos ou não para o sistema transicionar, respeitando as condições de balanço detalhado e ergodicidade das cadeias markovianas. Para este trabalho, foram estudados os algoritmos de Metropolis-Hasting e o algoritmo de banho térmico. | |||
=== Algorítmo de Metropolis-Hasting === | |||
O primeiro algoritmo utilizado para gerar as configurações do sistema foi o algoritmo de Metropolis-Hasting. O algoritmo escolhe repetidamente um novo estado para o sistema <math>\nu</math> e aceitando ou rejeitando ele de acordo com uma probabilidade de aceitação <math>A(\mu \rightarrow \nu)</math> de transitar de um estado antigo <math>\mu</math> para o novo estado <math>\nu</math>. O algoritmo que iremos descrever utiliza a dinâmica de inversão única de spins. | |||
Temos que a condição de balanceamento detalhado é dada por <ref>M. E. J. Newman, G. T. Barkema, "Monte Carlo Methods in Statistical Physics". Oxford University Press Inc., New York, 1999.</ref>: | |||
<math>\frac{A(\mu \rightarrow \nu)}{A(\nu \rightarrow \mu)} = e^{-\beta \Delta E}, \qquad (3)</math> | |||
onde <math>\Delta E = E_\nu - E_\mu</math> é a diferença de energia entre o novo e o antigo estado. | |||
Vamos supor que tenhamos os estados <math>\mu</math> e <math>\nu</math> e que temos a relação de energias: <math>E_\mu < E_\nu</math>. Então, a maior das duas chances de aceitação é <math>A(\nu \rightarrow \mu)</math>, portanto iremos igualar essa probabilidade a 1. | |||
Para que <math>(3)</math> seja respeitada, iremos definir o valor de <math>A(\mu \rightarrow \nu)</math> como <math>e^{-\beta \Delta E}</math>. Temos, assim, o algoritmo de Metropolis-Hasting: | |||
<math>A(\mu \rightarrow \nu) = \begin{cases} | |||
e^{-\beta \Delta E}, \qquad \text{se } \Delta E > 0\\\\ | |||
1, \qquad \qquad \text{caso contrario}. | |||
\end{cases}</math> | |||
Dessa forma, sempre que tivermos um estado cuja energia seja menor do que a do estado atual, iremos aceitar a transição, mas se a energia for maior, teremos uma pequena probabilidade de trocarmos de estado. | |||
=== Algoritmo de Banho Térmico === | |||
O algoritmo de Metropolis-Hasting para inversão única de spins é eficaz para o modelo de Potts em baixos valores de <math>Q</math> ou temperaturas acima da temperatura crítica, entretanto para valores altos de <math>Q</math> ou baixas temperaturas o algoritmo falha em convergir o sistema rapidamente para o estado estacionário. | |||
Considerando um caso onde <math>Q = 100</math> e um spin que possui 4 vizinhos, se todos os vizinhos do spin possuem valores diferentes uns do outro e do próprio spin, poderá levar em média <math>100/4 = 25</math> passos de Monte Carlo para sortear um novo valor de <math>q</math> que tem a transição aceita, e dessa forma o algoritmo irá demorar mais tempo para alcançar a configuração de equilíbrio do sistema. A dificuldade de aceitar transições é maior ainda para baixas temperaturas, onde a probabilidade de transicionar para um novo estado tem um peso maior para qualquer <math>q</math> diferente dos spins da vizinhança, dessa maneira poderá demorar 96 passos para gerar um spin que seja igual a algum spin da vizinhança e realizar a transição. Para contornar este problema podemos utilizar o algoritmo de banho térmico. | |||
O algoritmo de banho térmico, assim como o metropolis, é um algoritmo em que mudamos um spin por vez. O algoritmo segue as seguintes etapas: primeiro escolhemos um spin na rede (<math>i</math>), e independente do seu valor atual, escolhemos um novo valor para <math>s_i</math>. Esse novo valor será aceito, ou não, de acordo com os pesos de Boltzmann. Temos que no algoritmo de Banho Térmico nós atribuímos um valor <math>n</math>, entre 1 e <math>q</math>, ao spin com uma probabilidade | |||
<math>A(\mu \rightarrow \nu) = \frac{e^{-\beta E_{\nu}}}{\sum_{m=1}^q e^{-\beta E_m}} ,</math> | |||
onde <math>E_n</math> é a energia do sistema quando <math>s_i = n</math> e o somatório é dado em todas energias possíveis. Pelo fato desse algoritmo permitir que o spin assuma qualquer valor ele satisfaz a condição de ergodicidade. Temos que <math>A(\mu \rightarrow \nu) = a_{\nu}</math> e <math>A(\nu \rightarrow \mu) = a_{\mu}</math>, assim, pela descrição do algoritmo temos | |||
<math>\frac{A(\mu \rightarrow \nu)}{A(\nu \rightarrow \mu)} = \frac{a_{\nu}}{a_{\mu}} = \frac{e^{-\beta E_{\nu}}}{\sum_{m=1}^q e^{-\beta E_m}} \times \frac{\sum_{m=1}^q e^{-\beta E_m}}{e^{-\beta E_{\mu}}} = e^{-\beta \Delta E}.</math> | |||
Ou seja, o algoritmo de banho térmico respeita a condição de balanço detalhado. | |||
Veremos que para valores pequenos de <math>q</math> (como <math>q = 2</math>, que é o modelo de Ising), o algoritmo de Metropolis é mais eficiente. Porém, para valores altos de <math>q</math> ou altas temperaturas o algoritmo de banho térmico é mais eficiente. | |||
=== Implementação === | |||
Neste trabalho, o modelo de Potts foi estudado em uma rede quadrada 2D com vizinhança de von Neumann para primeiros vizinhos e condições de contorno periódicas. A quantidade de spins no modelo é <math>N = L\times L</math> com interações ferromagnéticas e <math>J = 1</math>, favorecendo vizinhanças de spins que compartilham o mesmo valor de <math>q</math> para minimizar a energia do sistema e <math>\beta = 1</math>. Em cada passo temporal, são realizadas <math>L^2</math> iterações do algoritmo de aceitação do Metropolis ou do Banho Térmico. Definimos Passo de Monte Carlo (MCS) como cada um desses passos temporais. Em cada passo de Monte Carlo, todos os sítios tem a probabilidade de realizar uma troca. | |||
== Resultados == | |||
Foram executadas simulações do modelo de Potts com <math>L = 64</math> e com <math>Q \in [2, 10]|Q\in\mathbb{Z}</math>. Foram feitas medidas das "magnetizações" do sistema e da energia total. A ideia de magnetização só tem sentido direto quando <math>Q = 2</math> (mesmo caso do modelo de Ising), mas para <math>Q > 2</math> a magnetização indica apenas para qual direção o sistema está mais alinhado. Contudo, a medida de relevância para os casos em que <math>Q > 2</math> é na verdade a susceptibilidade magnética, que ainda indica com qual facilidade o sistema muda seu alinhamento e também pode indicar a transição de fase. Abaixo seguem gráficos das energias totais do sistema com o algoritmo de banho térmico e o algoritmo de Metropolis. | |||
=== Casos para Q < 5 === | |||
==== Correspondência com o modelo de Ising ==== | |||
{| class="wikitable" style="text-align: center;" | |||
!colspan="2"|Medidas de energia, calor específico e susceptibilidade magnética para Q = 2 e L = 64 utilizando algoritmo de Metropolis | |||
|- | |||
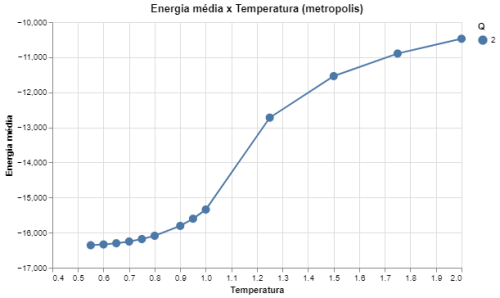
|[[Arquivo: energia_metropolis_q2.png|thumb|upright=4|none|alt=Alt text|Energia média em função da temperatura para Q = 2 e L = 64.|500px]] | |||
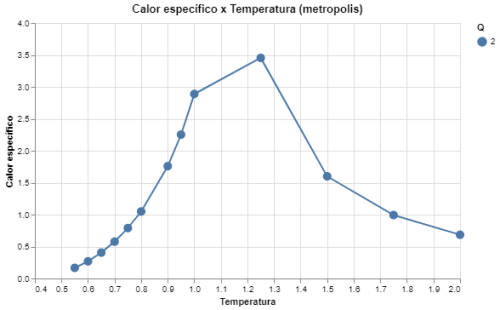
|[[Arquivo: desvio_energia_q2_.png|thumb|upright=4|none|alt=Alt text|Calor específico em função da temperatura para Q = 2 e L = 64|500px]] | |||
|- | |||
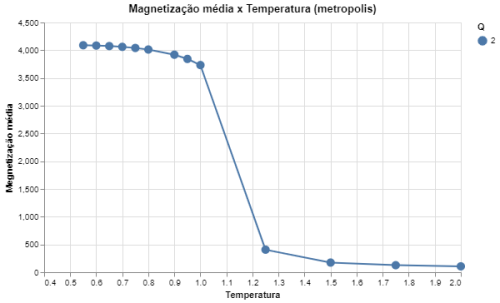
|[[Arquivo: mag_metropolis_q2.png|thumb|upright=4|none|alt=Alt text|Média do valor absoluto da magnetização em função da temperatura para Q = 2 e L = 64|500px]] | |||
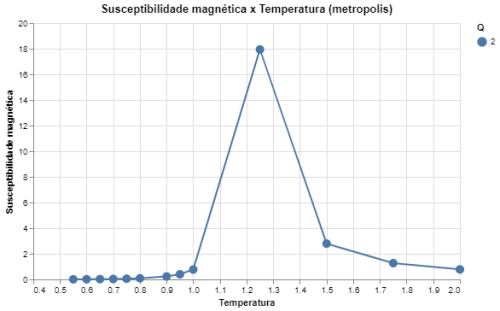
|[[Arquivo: desvio_mag_metropolis_q2.png|thumb|center|upright=4|none|alt=Alt text|Susceptibilidade magnética em função da temperatura para Q = 2 e L = 64|500px]] | |||
|- | |||
|} | |||
Podemos ver que os dados resultantes das simulações para o modelo de Potts com <math>Q = 2</math> de fato recriam o comportamento esperado pelo modelo de Ising. Observamos que tanto o calor específico como a susceptibilidade magnética aumentam drásticamente conforme se aproximam de <math>T = 1,1</math>. Como foi elaborado acima, o modelo de Ising tem a hamiltoniana igual a hamiltoniana do modelo de Potts a menos de uma constante, que é equivalente a <math>\sum_{\langle i, j\rangle}\frac{J}{2}</math>, o que corrobora que a temperatura crítica para o modelo de Potts, com <math>Q = 2</math> seja aproximadamente <math>T_c \approx 1,1</math>. | |||
==== Demais casos ==== | |||
{| class="wikitable" style="text-align: center;" | |||
!colspan="2"|Medidas de energia e magnetização para Q = {2,3,4} e L = 64 utilizando o algoritmo de Metropolis | |||
|- | |||
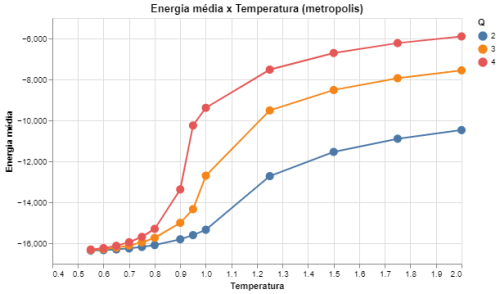
|[[Arquivo: energia_metropolis_q234.png|thumb|upright=4|none|alt=Alt text|Energia média em função da temperatura para Q = {2,3,4} e L = 64.|500px]] | |||
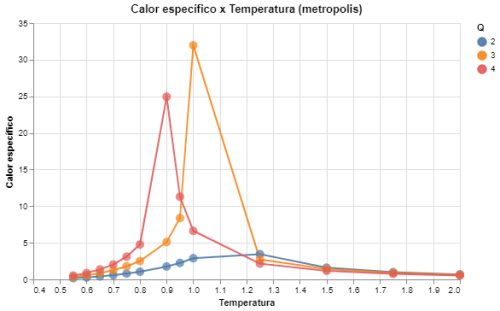
|[[Arquivo: desvio_energia_metropolis_q234.png|thumb|upright=4|none|alt=Alt text|Calor específico em função da temperatura para Q = {2,3,4} e L = 64|500px]] | |||
|- | |||
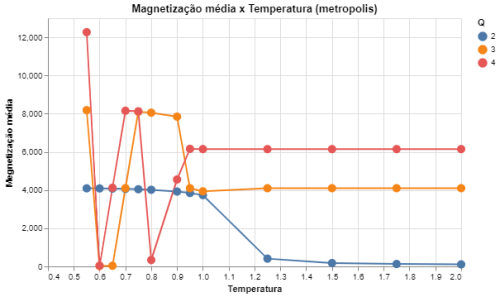
|[[Arquivo: mag_metropolis_q234.png|thumb|upright=4|none|alt=Alt text|Média do valor absoluto da magnetização em função da temperatura para Q = {2,3,4} e L = 64|500px]] | |||
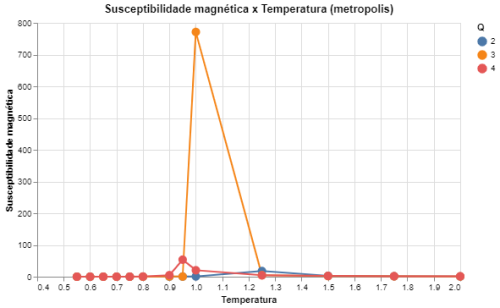
|[[Arquivo: desvio_mag_metropolis_q234.png|thumb|upright=4|none|alt=Alt text|Susceptibilidade magnética em função da temperatura para Q = {2,3,4} e L = 64|500px]] | |||
|- | |||
|} | |||
{| class="wikitable" style="text-align: center;" | |||
!colspan="2"|Medidas de energia e magnetização para Q = {2,3,4} e L = 64 utilizando o algoritmo de banho térmico | |||
|- | |||
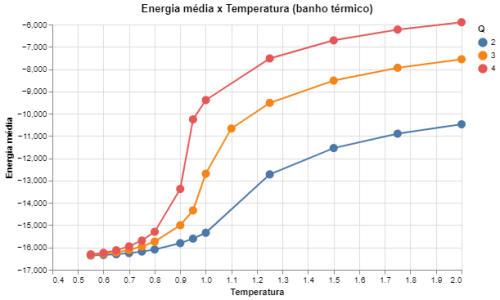
|[[Arquivo: energia_heatbath_q234.png|thumb|upright=4|none|alt=Alt text|Energia média em função da temperatura para Q = {2,3,4} e L = 64.|500px]] | |||
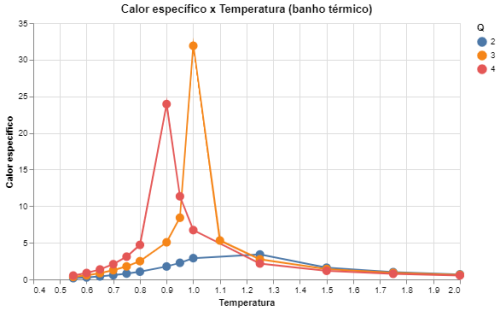
|[[Arquivo: desvio_energia_heatbath_q234.png|thumb|upright=4|none|alt=Alt text|Calor específico em função da temperatura para Q = {2,3,4} e L = 64|500px]] | |||
|- | |||
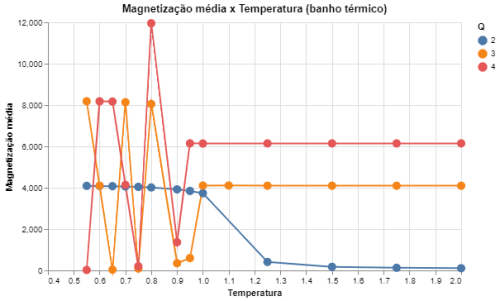
|[[Arquivo: mag_heatbath_q234.png|thumb|upright=4|none|alt=Alt text|Média do valor absoluto da magnetização em função da temperatura para Q = {2,3,4} e L = 64|500px]] | |||
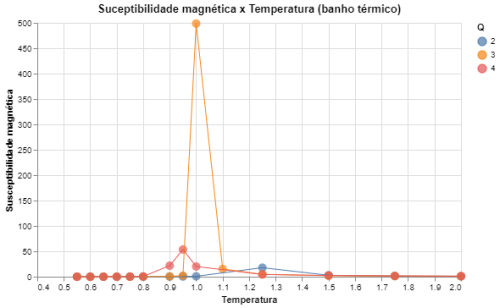
|[[Arquivo: desvio_mag_heatbath_q234.png|thumb|upright=4|none|alt=Alt text|Susceptibilidade magnética em função da temperatura para Q = {2,3,4} e L = 64|500px]] | |||
|- | |||
|} | |||
Agrupamos aqui os resultados obtidos para <math>Q \leq 4</math> porque se descobriu que para o caso bidimensional o modelo de Potts muda de tipo de transição de fase para <math>Q > 4</math>, passando a apresentar uma transição de primeira ordem<ref name = ARTIGO_BARKEMA>Gerard Barkema, Jan de Boer, Numerical Study of Phase Transitions in Potts Models, 1991</ref>. Como mostrado por Barkema <ref name = ARTIGO_BARKEMA></ref>, a transição de fase ocorre em temperaturas críticas que variam para cada <math>Q</math>, e aqui encontramos que são aproximadamente <math>1,0</math> para <math>Q=3</math>, <math>0,9</math> para <math>Q = 4</math>, e <math>1,1</math> para <math>Q = 2</math> como dito acima. | |||
=== Casos para Q > 4 === | |||
{| class="wikitable" style="text-align: center;" | |||
!colspan="2"|Medidas de energia e magnetização para Q = {5,6,7,8,9,10} e L = 64 utilizando o algoritmo de Metropolis | |||
|- | |||
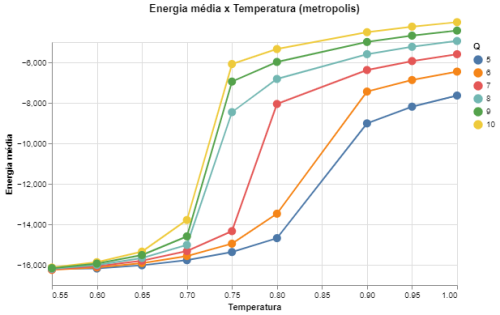
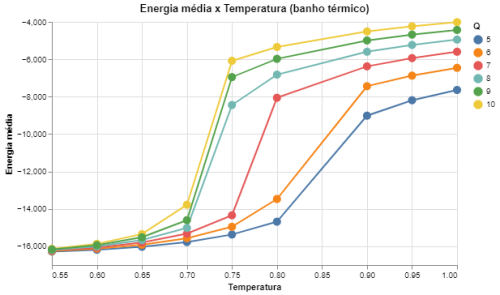
|[[Arquivo: energia_metropolis_q5678910.png|thumb|upright=4|none|alt=Alt text|Energia média em função da temperatura para Q = {5,6,7,8,9,10} e L = 64.|500px]] | |||
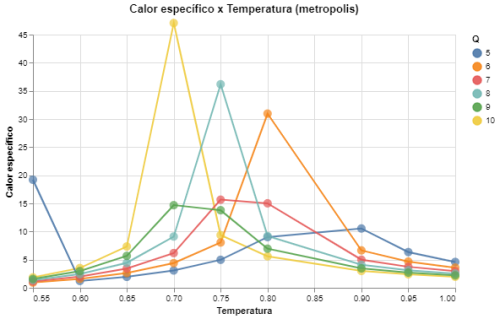
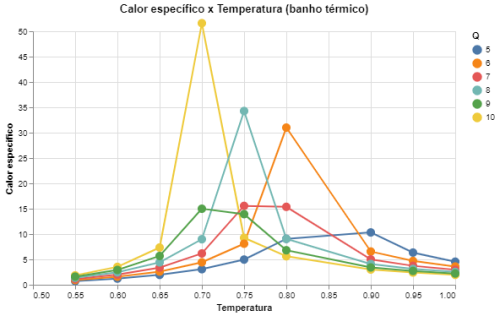
|[[Arquivo: desvio_energia_metropolis_q5678910.png|thumb|upright=4|none|alt=Alt text|Calor específico em função da temperatura para Q = {5,6,7,8,9,10} e L = 64|500px]] | |||
|- | |||
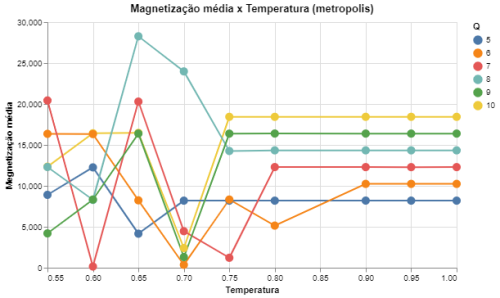
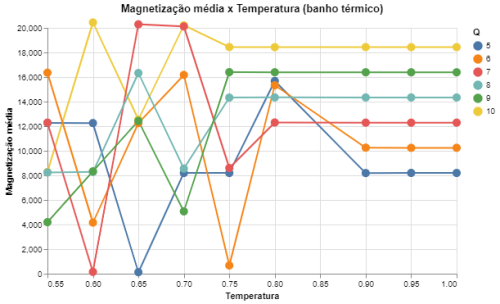
|[[Arquivo: mag_metropolis_q5678910.png|thumb|upright=4|none|alt=Alt text|Média do valor absoluto da magnetização em função da temperatura para Q = {5,6,7,8,9,10} e L = 64|500px]] | |||
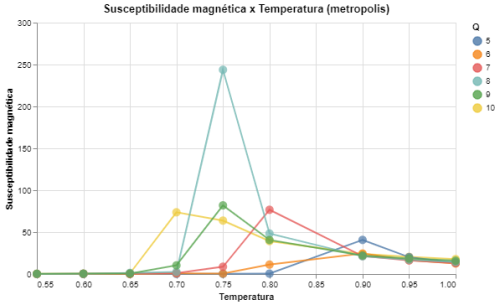
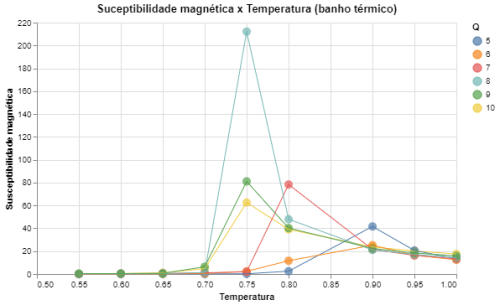
|[[Arquivo: desvio_mag_metropolis_q5678910.png|thumb|upright=4|none|alt=Alt text|Susceptibilidade magnética em função da temperatura para Q = {5,6,7,8,9,10} e L = 64|500px]] | |||
|- | |||
|} | |||
{| class="wikitable" style="text-align: center;" | |||
!colspan="2"|Medidas de energia e magnetização para Q = {5,6,7,8,9,10} e L = 64 utilizando o algoritmo de banho térmico | |||
|- | |||
|[[Arquivo: energia_heatbath_q5678910.png|thumb|upright=4|none|alt=Alt text|Energia média em função da temperatura para Q = {5,6,7,8,9,10} e L = 64.|500px]] | |||
|[[Arquivo: desvio_energia_heatbath_q5678910.png|thumb|upright=4|none|alt=Alt text|Calor específico em função da temperatura para Q = {5,6,7,8,9,10} e L = 64|500px]] | |||
|- | |||
|[[Arquivo: mag_heatbath_q5678910.png|thumb|upright=4|none|alt=Alt text|Média do valor absoluto da magnetização em função da temperatura para Q = {5,6,7,8,9,10} e L = 64|500px]] | |||
|[[Arquivo: desvio_mag_heatbath_q5678910.png|thumb|upright=4|none|alt=Alt text|Susceptibilidade magnética em função da temperatura para Q = {5,6,7,8,9,10} e L = 64|500px]] | |||
|- | |||
|} | |||
De acordo com a previsão de Barkema<ref name = ARTIGO_BARKEMA></ref> a transição de fase para <math>Q > 4</math> passa a ser de primeira ordem, e nossos resultados estão de acordo com isso, pois há uma variação muito mais brusca nas curvas das energias médias do sistema em comparação às variações para <math>Q \leq 4</math>, que por sua vez tem uma curva muito mais suave. Além disso, podemos ver que o comportamento dos desvios se torna muito mais único para cada <math>Q</math>, isso porque a transição ocorre de maneira contínua e assim há apenas um pico nos valores das energias, que por sua vez se torna fortemente dependente de <math>Q</math>. | |||
Outro comentário importante é que os resultados obtidos utilizando o algoritmo de Metropolis e o algoritmo de banho térmico são extremamente similares, apenas havendo uma diferença nos desvios das medidas, que são menores para o algoritmo de banho térmico já que este tem uma aceitação das trocas de spins muito mais alta que a do Metropolis. Isso se observa em todos os <math>Q</math>. | |||
=== Comparação entre algoritmo de Metropolis-Hasting e banho térmico para baixas temperaturas === | |||
{| class="wikitable" style="text-align: center;" | |||
!colspan="2"|Algoritmo de Metropolis (azul) X Algoritmo de banho térmico (vermelho) para Q = 2 e T = 0.25 e T = 0.3 | |||
|- | |||
|[[Arquivo: energia_metropolis_x_heathbath_Q2_T0.25.png|thumb|upright=4|none|alt=Alt text|Energia função dos passos de Monte Carlo para Q = 2, L = 64 e T = 0.25|500px]] | |||
|[[Arquivo: energia_metropolis_x_heathbath_Q2_T0.3.png|thumb|upright=4|none|alt=Alt text|Energia função dos passos de Monte Carlo para Q = 2, L = 64 e T = 0.3|500px]] | |||
|- | |||
|} | |||
{| class="wikitable" style="text-align: center;" | |||
!colspan="2"|Algoritmo de Metropolis (azul) X Algoritmo de banho térmico (vermelho) para Q = 3 e T = 0.25 e T = 0.3 | |||
|- | |||
|[[Arquivo: energia_metropolis_x_heathbath_Q3_T0.25.png|thumb|upright=4|none|alt=Alt text|Energia função dos passos de Monte Carlo para Q = 3, L = 64 e T = 0.25|500px]] | |||
|[[Arquivo: energia_metropolis_x_heathbath_Q3_T0.3.png|thumb|upright=4|none|alt=Alt text|Energia função dos passos de Monte Carlo para Q = 3, L = 64 e T = 0.3|500px]] | |||
|- | |||
|} | |||
{| class="wikitable" style="text-align: center;" | |||
!colspan="2"|Algoritmo de Metropolis (azul) X Algoritmo de banho térmico para Q = 4 e T = 0.3 e T = 0.4 | |||
|- | |||
|[[Arquivo: energia_metropolis_x_heathbath_Q4_T0.3.png|thumb|upright=4|none|alt=Alt text|Energia função dos passos de Monte Carlo para Q = 4, L = 64 e T = 0.3|500px]] | |||
|[[Arquivo: energia_metropolis_x_heathbath_Q4_T0.4.png|thumb|upright=4|none|alt=Alt text|Energia função dos passos de Monte Carlo para Q = 4, L = 64 e T = 0.4|500px]] | |||
|- | |||
|} | |||
Podemos observar que no caso do algoritmo de Metropolis o sistema tem extrema dificuldade de trocar de estado, ficando quase constantemente no mesmo valor de energia. O algoritmo de banho térmico porém apresenta uma flutuação muito mais coerente com a distribuição de Boltzmann para o sistema nessa temperatura. Isso mostra que para baixas temperaturas o algoritmo do banho térmico é muito mais eficiente que o de Metropolis, que por sua vez é impraticável para temperaturas muito baixas. | |||
É importante ressaltar que tivemos que mudar a quantidade de passos de Monte Carlo para algumas das simulações para que o sistema alcançasse o estado estcionário com o algoritmo de banho térmico. Isso porque o algoritmo de banho térmico favorece a formação de faixas dominadas por dois ou mais <math>q</math>, o que faz com que o sistema demore muito até que uma dessas faixas consiga alinhar a(s) outra(s) e então levar o sistema para o estado estacionário. | |||
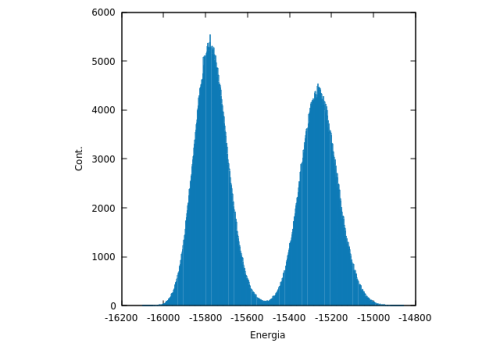
Quando as simulações passam por esses casos, observamos uma distribuição de energia com duas curvas normais: uma para o estado transiente do sistema em que as faixas causam um equilíbrio instável para o sistema e outra de menor energia que representa o estado de equilíbrio do sistema após uma das faixas alinhar a outra. Veja: | |||
[[Arquivo: histograma_HB_Q5_T07.png|thumb|center|upright=4|none|alt=Alt text| Histograma para <math> Q = 5</math> e <math>T = 0.7</math> executado com o algoritmo de banho térmico mostrando a formação de duas curvas normais.|500px]] | |||
{| class="wikitable" style="text-align: center;" | |||
!colspan="2"|Animações comparando a evolução do sistema usando o algoritmo de Metropolis (esquerda) e o algoritmo de banho térmico (direita). | |||
|- | |||
|[[Arquivo: Q10_T025_MT.gif|thumb|upright=4|none|alt=Alt text|Evolução do sistema com o algoritmo de Metropolis com <math>Q = 10</math> e <math>T = 0.25</math>.|500px]] | |||
|[[Arquivo: Q10_T025_HB.gif|thumb|upright=4|none|alt=Alt text|Evolução do sistema com o algoritmo de banho térmico com <math>Q = 10</math> e <math>T = 0.25</math>.|500px]] | |||
|- | |||
|} | |||
Note que o sistema com o algoritmo de Metropolis fica "preso" em um estado com uma faixa de <math>q = 2</math> no meio de um mar de spins <math>q = 1</math>, mas não consegue se alinhar até o final da animação. Isso representa um estado de equilíbrio instável para o modelo, mas o sistema fica preso nessa condição por limitação do algoritmo de Metropolis, que tem baixíssima eficiência para baixas temperaturas. O sistema com o algoritmo de banho térmico por outro lado consegue "dissolver" os aglomerados de spins diferentes que mostra haviam no começo da animação e no fim da animação todos os spins estão alinhados, demonstrando a melhor eficiência desse algoritmo nessas condições. | |||
== Otimizações Computacionais == | |||
Essa seção é focada em algumas otimizações computacionais que podemos fazer ao simular sistemas de rede. Os "snippets" de códigos estão em C, mas a ideia pode ser adaptada para qualquer linguagem de programação. | |||
=== Redes === | |||
Uma boa sugestão ao criar a topologia do sistema é utilizar um "array" unidimensional ao invés de bidimensional. Como estamos falando de uma rede quadrada de tamanho <math>L \times L = L^2</math> podemos fazer | |||
<source lang=C> | |||
int sitio[L*L]; | |||
</source> | |||
no lugar de | |||
<source lang=C> | |||
int sitio[L][L]; | |||
</source> | |||
Uma praticidade que ganhamos com isso é que diminuímos as componentes que precisamos utilizar para diferenciar cada sítio na rede, sendo necessário apenas um número aleatório para identificar o sítio. Outra sugestão é criar uma matriz de vizinhos, pois nas simulações desses sistemas geralmente precisamos saber a configuração deles. Nos vizinhos criaremos um "array" bidimensional, uma coordenada indicará o sitio que queremos e a outra indicará qual dos quatro vizinhos estamos lidando: | |||
<source lang=C> | |||
int viz[L*L][4]; | |||
</source> | |||
Então por lidarmos com os nossos sítios em um "array" unidimensional e condições periódicas utilizamos as seguintes relações que determinam a posição de cada vizinho nessa matriz. | |||
<source lang=C> | |||
for(i=0; i<L*L; i++) | |||
{ | |||
viz[i][0] = (i-L+(L*L))%(L*L); | |||
viz[i][1] = (i+1)%L + (i/L)*L; | |||
viz[i][2] = (i+L)%(L*L); | |||
viz[i][3] = (i-1+L)%L + (i/L)*L; | |||
} | |||
</source> | |||
Assim, se necessitarmos comparar com apenas um vizinho utilizamos o numero correspondente a ele, e se precisarmos comparar com todos podemos fazer um "loop". Lembrando que esse "array" guarda a posição dos vizinhos, se quisermos, por exemplo, associar um valor <math>q</math> ao vizinho 3 do sítio <math>i</math> fazemos da forma | |||
<source lang=C> | |||
sitio[viz[i][3]] = q; | |||
</source> | |||
=== Redução de "if"s === | |||
No Modelo de Potts nós possuímos uma delta de Kronecker. Iremos subtrair <math>J</math> da nossa energia se o valor do sítio for igual ao de um vizinho. A maneira mais direta de se pensar em simular essa parte do sistema é utilizando condicionais "if/else", da forma | |||
<source lang=C> | |||
for(int j=0; j<_Q; j++) | |||
{ | |||
for(int k=0; k<4; k++) | |||
{ | |||
E1 = 0; | |||
if(j==spin[neigh[site][k]]) | |||
{ | |||
E1-=J; | |||
} | |||
} | |||
E2 += exp(-E1/(KB*_TEMP)); | |||
} | |||
</source> | |||
Entretanto, Para valores grandes de <math>q</math> esses condicionais "if"s resultarão em um alto custo computacional. Como temos uma delta de Kronecker no sistema podemos utilizar dela dentro do programa. Primeiro definimos o array bidimensional como a delta de kronecker da forma | |||
<source lang=C> | |||
for(i=0; i<_Q; i++) | |||
{ | |||
for(j=0; j<_Q; j++) | |||
{ | |||
if(i==j) | |||
{ | |||
kronecker[i][j] = 1; | |||
} | |||
else | |||
{ | |||
kronecker[i][j] = 0; | |||
} | |||
} | |||
} | |||
</source> | |||
Note que utilizamos "if/else", porém essa parte do código executa apenas uma vez. E então usamos esse "array" para otimizar as comparações: | |||
<source lang=C> | |||
for(j=0; j<_Q; j++) | |||
{ | |||
E1 = 0; | |||
for(k=0; k<4; k++) | |||
{ | |||
E1-=J*kronecker[j][spin[neigh[site][k]]]; | |||
} | |||
E2 += exp(-E1/(KB*_TEMP)); | |||
} | |||
</source> | |||
Assim obtemos um melhor desempenho computacional, já que não temos uma grande quantidade de "if"" no código. Também utilizamos de forma mais clara a delta de kronecker do nosso hamiltoniano. | |||
=== Função de Visualização === | |||
Podemos estar interessados em ver a evolução do nosso sistema. Podemos plotar diretamente do programa sem gerar os dados e plotar depois. Definimos essa função da forma | |||
<source lang=C> | |||
void visualize(int *spin) | |||
{ | |||
int i; | |||
printf("unset xtics\nunset ytics\n"); | |||
printf("set size square\n"); | |||
printf("set xrange [0:%d]\nset yrange [0:%d]\n",L-1,L-1); | |||
printf("pl '-' matrix w image\n"); | |||
for(i=L2-1; i>=0; i--) | |||
{ | |||
printf("%d ", spin[i]); | |||
if(i%L == 0) | |||
{ | |||
printf("\n"); | |||
} | |||
} | |||
printf("e\n\n"); | |||
} | |||
</source> | |||
onde a função recebe o sitio. Utilizando um "pipe" redirecionamos a saida diretamente para a o gnuplot. Podemos também não querer plotar sempre, assim definimos uma diretiva que responde a compilação do programa | |||
<source lang=C> | |||
#ifdef VIEW | |||
if(mcs % 10 == 0) | |||
{ | |||
printf("set title 'T = %d MCS'\n", mcs); | |||
visualize(spin); | |||
} | |||
#endif | |||
</source> | |||
Assim, se na linha de compilação tiver a opção <source lang=sh> -DVIEW </source> o programa irá, a cada <math>10 mcs</math>, plotar a configuração do sistema. Essa opção as vezes se torna importante para visualizar se nosso sistema esta evoluindo da forma que estamos esperando. | |||
== Programas Utilizados == | |||
Programas na linguagem C. Para utilizar os programas, abra o terminal e compile da forma | |||
<source lang=sh> | |||
$ gcc prog.c -lm | |||
</source> | |||
Onde ''prog.c'' é o programa que deseja utilizar. É necessário que o programa e a biblioteca com funções para simulações de Monte Carlo estejam no mesmo diretório no momento da compilação. Execute da seguinte maneira | |||
<source lang=sh> | |||
$ ./a.out Q TEMP | |||
</source> | |||
onde o segundo termo é o estado Q do sistema e o terceiro é a temperatura do sistema. Os programas possuem uma diretiva de compilação para visualização do sistema ao decorrer da execução. Para utilizar é necessário ter o gnuplot <ref name=GNUPLOT>https://fiscomp.if.ufrgs.br/index.php/Gnuplot</ref> instalado e compilar da forma | |||
<source lang=sh> | |||
$ gcc -DVIEW prog.c -lm | |||
</source> | |||
e então executar da maneira | |||
<source lang=sh> | |||
$ ./a.out Q TEMP | gnuplot | |||
</source> | |||
Entretanto com a visualização no gnuplot o programa demora mais para executar, então é recomendado diminuir os tempos de transiente (''TRAN'') e medidas (''TMAX'') caso se queira observar a simulação inteira. | |||
O script possui alguns exemplos de execução através de diferentes estados e temperaturas do sistema. Copie o conteudo em um arquivo e então o deixar executável: | |||
<source lang=sh> | |||
$ chmod +x script.sh | |||
</source> | |||
e então com o programa compilado pode executar da forma | |||
<source lang=sh> | |||
$ ./script.sh | |||
</source> | |||
[[Potts Metropolis]] | |||
[[Potts Banho Térmico]] | |||
[[Biblioteca com funções em C para simulações de Monte Carlo]] | |||
[[Script em bash para gerar os dados]] | |||
== Referências == | |||
<references/> | |||
Edição atual tal como às 10h43min de 25 de maio de 2021
Modelo de Potts
O Modelo
O "modelo de Potts de Q-estados" trata de um sistema de rede com N spins interagentes , onde um spin pode assumir valores discretos . Cada spin do sistema está limitado a interagir com outros spins em sua vizinhança e a energia da interação entre dois spins e é dada pelo potencial
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta{(s_i,s_j)}} é a função delta de Kronecker e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J} é a constante de interação entre os spins. Dessa maneira, a interação entre dois spins vizinhos contabiliza um valor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -J} de energia ao sistema apenas se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_i = s_j} . A hamiltoniana do sistema é dada pela soma entre todas as interações entre spins vizinhos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} = -J\sum_{\langle i,j \rangle}{\delta{(s_i,s_j)}}}
Este modelo é tido como uma generalização natural do Modelo de Ising e para o caso Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q = 2} ambos modelos são equivalentes a menos de uma constante:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{ising} = \mathcal{H}_{potts} + \sum_{\langle i,j \rangle}\frac{J}{2} = -\frac{J}{2}\sum_{\langle i,j \rangle}[2\delta(s_i,s_j) - 1] }
Nesse caso, a interação entre dois spins Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_i} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_j} assume a mesma dinâmica do modelo de Ising a contribuição para a energia do sistema será
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(s_i,s_j) = \begin{cases} -\frac{J}{2}, \qquad \text{se } s_i = s_j \\ \frac{J}{2}, \qquad \text{se } s_i \neq s_j \end{cases}}
Motivações
Por muitos anos o modelo de Potts foi considerado um sistema que exibe transição de ordem e desordem de interesse apenas teórico, mas atualmente se sabe que as propriedades do modelo de Potts podem ser encontradas em sistemas reais e podem ser medidos através da realização de experimentos. O princípio básico na experimentação de sistemas de spin é o princípio da universalidade, onde busca-se identificar sistemas reais que pertencem a mesma classe de universalidade do modelo de spin em questão. Ou seja, medindo os expoentes críticos do experimento, encontramos sua classe.
Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q = 2 } sabemos que o modelo de Potts possui as propriedades do modelo de Ising. Em duas dimensões, foi provado [1] que um sistema absorvido de átomos de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle He^{4}} cobrindo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} de uma rede honeycomb de grafite exibe o mesmo expoente crítico do calor específico que o modelo de Ising. Esse mesmo sistema, mas agora cobrindo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} da rede exibe o comportamento do modelo de Potts para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q = 3 } . Outros estudos de sistemas absorvidos, como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_{2}} em uma rede 2D de grafite, mostram mostram comportamento da classe Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q = 4} . Também foi provado que polímeros que interagem em soluções, como processos de vulcanização [1] de polímeros ramificados tem a classe de universalidade para o modelo de Potts com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 \leq Q \leq 1} . Uma breve observação: o modelo de Potts de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} -estados generalizado não exige que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} seja um valor inteiro, mas neste trabalho só tratamos desse caso.
Modelo celular de Potts
Além da física de materiais, o modelo de Potts também é aplicado em biologia computacional para a simulação de células através do modelo celular de Potts. Esse modelo trata células como objetos deformáveis que podem mover, crescer ou até se dividir e pode simular o comportamento coletivo de células, estudando o surgimento de células cancerígenas e morfogênese.
A energia do sistema é descrita por
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} = -\sum_{\langle i,j \rangle}J_{\sigma_i,\sigma_j}\left(1-\delta_{\sigma_i,\sigma_j}\right) + \lambda\sum_{\sigma_i}\left(v(\sigma_i)-V(\sigma_i)\right)^2 }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} são posições da rede, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_{i}} é a célula na posição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J} é o coeficiente determinando a adesão de dois tipos diferentes de células, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v(\sigma)} é o volume da célula Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(\sigma)} é o volume padrão de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} determina a força da elasticidade volumétrica da célula. O modelo pode considerar ainda elasticidade de área e perímetro de cada célula.
Método de Monte Carlo
O método de Monte Carlo é aplicado ao modelo de Potts com o objetivo de gerar estados de equilíbrio para medir os observáveis do sistema. Os Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} spins são iniciados com valores aleatórios de Q na rede e o método de Monte Carlo escolhe arbitrariamente um spin Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_i} e gera um novo valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q\in Q | q \neq s_i} para o spin. A partir disso, através de algum algoritmo específico, se escolhe como os estados serão gerados e quais serão aceitos ou não para o sistema transicionar, respeitando as condições de balanço detalhado e ergodicidade das cadeias markovianas. Para este trabalho, foram estudados os algoritmos de Metropolis-Hasting e o algoritmo de banho térmico.
Algorítmo de Metropolis-Hasting
O primeiro algoritmo utilizado para gerar as configurações do sistema foi o algoritmo de Metropolis-Hasting. O algoritmo escolhe repetidamente um novo estado para o sistema Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} e aceitando ou rejeitando ele de acordo com uma probabilidade de aceitação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(\mu \rightarrow \nu)} de transitar de um estado antigo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} para o novo estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} . O algoritmo que iremos descrever utiliza a dinâmica de inversão única de spins.
Temos que a condição de balanceamento detalhado é dada por [2]:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{A(\mu \rightarrow \nu)}{A(\nu \rightarrow \mu)} = e^{-\beta \Delta E}, \qquad (3)}
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta E = E_\nu - E_\mu} é a diferença de energia entre o novo e o antigo estado.
Vamos supor que tenhamos os estados Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} e que temos a relação de energias: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_\mu < E_\nu} . Então, a maior das duas chances de aceitação é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(\nu \rightarrow \mu)} , portanto iremos igualar essa probabilidade a 1. Para que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (3)} seja respeitada, iremos definir o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(\mu \rightarrow \nu)} como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-\beta \Delta E}} . Temos, assim, o algoritmo de Metropolis-Hasting:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(\mu \rightarrow \nu) = \begin{cases} e^{-\beta \Delta E}, \qquad \text{se } \Delta E > 0\\\\ 1, \qquad \qquad \text{caso contrario}. \end{cases}}
Dessa forma, sempre que tivermos um estado cuja energia seja menor do que a do estado atual, iremos aceitar a transição, mas se a energia for maior, teremos uma pequena probabilidade de trocarmos de estado.
Algoritmo de Banho Térmico
O algoritmo de Metropolis-Hasting para inversão única de spins é eficaz para o modelo de Potts em baixos valores de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} ou temperaturas acima da temperatura crítica, entretanto para valores altos de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} ou baixas temperaturas o algoritmo falha em convergir o sistema rapidamente para o estado estacionário.
Considerando um caso onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q = 100} e um spin que possui 4 vizinhos, se todos os vizinhos do spin possuem valores diferentes uns do outro e do próprio spin, poderá levar em média Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100/4 = 25} passos de Monte Carlo para sortear um novo valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} que tem a transição aceita, e dessa forma o algoritmo irá demorar mais tempo para alcançar a configuração de equilíbrio do sistema. A dificuldade de aceitar transições é maior ainda para baixas temperaturas, onde a probabilidade de transicionar para um novo estado tem um peso maior para qualquer Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} diferente dos spins da vizinhança, dessa maneira poderá demorar 96 passos para gerar um spin que seja igual a algum spin da vizinhança e realizar a transição. Para contornar este problema podemos utilizar o algoritmo de banho térmico.
O algoritmo de banho térmico, assim como o metropolis, é um algoritmo em que mudamos um spin por vez. O algoritmo segue as seguintes etapas: primeiro escolhemos um spin na rede (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} ), e independente do seu valor atual, escolhemos um novo valor para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_i} . Esse novo valor será aceito, ou não, de acordo com os pesos de Boltzmann. Temos que no algoritmo de Banho Térmico nós atribuímos um valor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} , entre 1 e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} , ao spin com uma probabilidade
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(\mu \rightarrow \nu) = \frac{e^{-\beta E_{\nu}}}{\sum_{m=1}^q e^{-\beta E_m}} ,}
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n} é a energia do sistema quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_i = n} e o somatório é dado em todas energias possíveis. Pelo fato desse algoritmo permitir que o spin assuma qualquer valor ele satisfaz a condição de ergodicidade. Temos que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(\mu \rightarrow \nu) = a_{\nu}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(\nu \rightarrow \mu) = a_{\mu}} , assim, pela descrição do algoritmo temos
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{A(\mu \rightarrow \nu)}{A(\nu \rightarrow \mu)} = \frac{a_{\nu}}{a_{\mu}} = \frac{e^{-\beta E_{\nu}}}{\sum_{m=1}^q e^{-\beta E_m}} \times \frac{\sum_{m=1}^q e^{-\beta E_m}}{e^{-\beta E_{\mu}}} = e^{-\beta \Delta E}.}
Ou seja, o algoritmo de banho térmico respeita a condição de balanço detalhado.
Veremos que para valores pequenos de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} (como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q = 2} , que é o modelo de Ising), o algoritmo de Metropolis é mais eficiente. Porém, para valores altos de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} ou altas temperaturas o algoritmo de banho térmico é mais eficiente.
Implementação
Neste trabalho, o modelo de Potts foi estudado em uma rede quadrada 2D com vizinhança de von Neumann para primeiros vizinhos e condições de contorno periódicas. A quantidade de spins no modelo é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = L\times L} com interações ferromagnéticas e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J = 1} , favorecendo vizinhanças de spins que compartilham o mesmo valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} para minimizar a energia do sistema e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = 1} . Em cada passo temporal, são realizadas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2} iterações do algoritmo de aceitação do Metropolis ou do Banho Térmico. Definimos Passo de Monte Carlo (MCS) como cada um desses passos temporais. Em cada passo de Monte Carlo, todos os sítios tem a probabilidade de realizar uma troca.
Resultados
Foram executadas simulações do modelo de Potts com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = 64} e com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q \in [2, 10]|Q\in\mathbb{Z}} . Foram feitas medidas das "magnetizações" do sistema e da energia total. A ideia de magnetização só tem sentido direto quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q = 2} (mesmo caso do modelo de Ising), mas para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q > 2} a magnetização indica apenas para qual direção o sistema está mais alinhado. Contudo, a medida de relevância para os casos em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q > 2} é na verdade a susceptibilidade magnética, que ainda indica com qual facilidade o sistema muda seu alinhamento e também pode indicar a transição de fase. Abaixo seguem gráficos das energias totais do sistema com o algoritmo de banho térmico e o algoritmo de Metropolis.
Casos para Q < 5
Correspondência com o modelo de Ising
| Medidas de energia, calor específico e susceptibilidade magnética para Q = 2 e L = 64 utilizando algoritmo de Metropolis | |
|---|---|
Podemos ver que os dados resultantes das simulações para o modelo de Potts com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q = 2} de fato recriam o comportamento esperado pelo modelo de Ising. Observamos que tanto o calor específico como a susceptibilidade magnética aumentam drásticamente conforme se aproximam de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 1,1} . Como foi elaborado acima, o modelo de Ising tem a hamiltoniana igual a hamiltoniana do modelo de Potts a menos de uma constante, que é equivalente a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\langle i, j\rangle}\frac{J}{2}} , o que corrobora que a temperatura crítica para o modelo de Potts, com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q = 2} seja aproximadamente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c \approx 1,1} .
Demais casos
| Medidas de energia e magnetização para Q = {2,3,4} e L = 64 utilizando o algoritmo de Metropolis | |
|---|---|
| Medidas de energia e magnetização para Q = {2,3,4} e L = 64 utilizando o algoritmo de banho térmico | |
|---|---|
Agrupamos aqui os resultados obtidos para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q \leq 4} porque se descobriu que para o caso bidimensional o modelo de Potts muda de tipo de transição de fase para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q > 4} , passando a apresentar uma transição de primeira ordem[3]. Como mostrado por Barkema [3], a transição de fase ocorre em temperaturas críticas que variam para cada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} , e aqui encontramos que são aproximadamente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1,0} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q=3} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0,9} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q = 4} , e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1,1} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q = 2} como dito acima.
Casos para Q > 4
| Medidas de energia e magnetização para Q = {5,6,7,8,9,10} e L = 64 utilizando o algoritmo de Metropolis | |
|---|---|
| Medidas de energia e magnetização para Q = {5,6,7,8,9,10} e L = 64 utilizando o algoritmo de banho térmico | |
|---|---|
De acordo com a previsão de Barkema[3] a transição de fase para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q > 4} passa a ser de primeira ordem, e nossos resultados estão de acordo com isso, pois há uma variação muito mais brusca nas curvas das energias médias do sistema em comparação às variações para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q \leq 4} , que por sua vez tem uma curva muito mais suave. Além disso, podemos ver que o comportamento dos desvios se torna muito mais único para cada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} , isso porque a transição ocorre de maneira contínua e assim há apenas um pico nos valores das energias, que por sua vez se torna fortemente dependente de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} .
Outro comentário importante é que os resultados obtidos utilizando o algoritmo de Metropolis e o algoritmo de banho térmico são extremamente similares, apenas havendo uma diferença nos desvios das medidas, que são menores para o algoritmo de banho térmico já que este tem uma aceitação das trocas de spins muito mais alta que a do Metropolis. Isso se observa em todos os Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} .
Comparação entre algoritmo de Metropolis-Hasting e banho térmico para baixas temperaturas
| Algoritmo de Metropolis (azul) X Algoritmo de banho térmico (vermelho) para Q = 2 e T = 0.25 e T = 0.3 | |
|---|---|
| Algoritmo de Metropolis (azul) X Algoritmo de banho térmico (vermelho) para Q = 3 e T = 0.25 e T = 0.3 | |
|---|---|
| Algoritmo de Metropolis (azul) X Algoritmo de banho térmico para Q = 4 e T = 0.3 e T = 0.4 | |
|---|---|
Podemos observar que no caso do algoritmo de Metropolis o sistema tem extrema dificuldade de trocar de estado, ficando quase constantemente no mesmo valor de energia. O algoritmo de banho térmico porém apresenta uma flutuação muito mais coerente com a distribuição de Boltzmann para o sistema nessa temperatura. Isso mostra que para baixas temperaturas o algoritmo do banho térmico é muito mais eficiente que o de Metropolis, que por sua vez é impraticável para temperaturas muito baixas.
É importante ressaltar que tivemos que mudar a quantidade de passos de Monte Carlo para algumas das simulações para que o sistema alcançasse o estado estcionário com o algoritmo de banho térmico. Isso porque o algoritmo de banho térmico favorece a formação de faixas dominadas por dois ou mais Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} , o que faz com que o sistema demore muito até que uma dessas faixas consiga alinhar a(s) outra(s) e então levar o sistema para o estado estacionário. Quando as simulações passam por esses casos, observamos uma distribuição de energia com duas curvas normais: uma para o estado transiente do sistema em que as faixas causam um equilíbrio instável para o sistema e outra de menor energia que representa o estado de equilíbrio do sistema após uma das faixas alinhar a outra. Veja:
Note que o sistema com o algoritmo de Metropolis fica "preso" em um estado com uma faixa de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q = 2} no meio de um mar de spins Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q = 1} , mas não consegue se alinhar até o final da animação. Isso representa um estado de equilíbrio instável para o modelo, mas o sistema fica preso nessa condição por limitação do algoritmo de Metropolis, que tem baixíssima eficiência para baixas temperaturas. O sistema com o algoritmo de banho térmico por outro lado consegue "dissolver" os aglomerados de spins diferentes que mostra haviam no começo da animação e no fim da animação todos os spins estão alinhados, demonstrando a melhor eficiência desse algoritmo nessas condições.
Otimizações Computacionais
Essa seção é focada em algumas otimizações computacionais que podemos fazer ao simular sistemas de rede. Os "snippets" de códigos estão em C, mas a ideia pode ser adaptada para qualquer linguagem de programação.
Redes
Uma boa sugestão ao criar a topologia do sistema é utilizar um "array" unidimensional ao invés de bidimensional. Como estamos falando de uma rede quadrada de tamanho Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L \times L = L^2} podemos fazer
int sitio[L*L];
no lugar de
int sitio[L][L];
Uma praticidade que ganhamos com isso é que diminuímos as componentes que precisamos utilizar para diferenciar cada sítio na rede, sendo necessário apenas um número aleatório para identificar o sítio. Outra sugestão é criar uma matriz de vizinhos, pois nas simulações desses sistemas geralmente precisamos saber a configuração deles. Nos vizinhos criaremos um "array" bidimensional, uma coordenada indicará o sitio que queremos e a outra indicará qual dos quatro vizinhos estamos lidando:
int viz[L*L][4];
Então por lidarmos com os nossos sítios em um "array" unidimensional e condições periódicas utilizamos as seguintes relações que determinam a posição de cada vizinho nessa matriz.
for(i=0; i<L*L; i++)
{
viz[i][0] = (i-L+(L*L))%(L*L);
viz[i][1] = (i+1)%L + (i/L)*L;
viz[i][2] = (i+L)%(L*L);
viz[i][3] = (i-1+L)%L + (i/L)*L;
}
Assim, se necessitarmos comparar com apenas um vizinho utilizamos o numero correspondente a ele, e se precisarmos comparar com todos podemos fazer um "loop". Lembrando que esse "array" guarda a posição dos vizinhos, se quisermos, por exemplo, associar um valor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} ao vizinho 3 do sítio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} fazemos da forma
sitio[viz[i][3]] = q;
Redução de "if"s
No Modelo de Potts nós possuímos uma delta de Kronecker. Iremos subtrair Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J} da nossa energia se o valor do sítio for igual ao de um vizinho. A maneira mais direta de se pensar em simular essa parte do sistema é utilizando condicionais "if/else", da forma
for(int j=0; j<_Q; j++)
{
for(int k=0; k<4; k++)
{
E1 = 0;
if(j==spin[neigh[site][k]])
{
E1-=J;
}
}
E2 += exp(-E1/(KB*_TEMP));
}
Entretanto, Para valores grandes de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} esses condicionais "if"s resultarão em um alto custo computacional. Como temos uma delta de Kronecker no sistema podemos utilizar dela dentro do programa. Primeiro definimos o array bidimensional como a delta de kronecker da forma
for(i=0; i<_Q; i++)
{
for(j=0; j<_Q; j++)
{
if(i==j)
{
kronecker[i][j] = 1;
}
else
{
kronecker[i][j] = 0;
}
}
}
Note que utilizamos "if/else", porém essa parte do código executa apenas uma vez. E então usamos esse "array" para otimizar as comparações:
for(j=0; j<_Q; j++)
{
E1 = 0;
for(k=0; k<4; k++)
{
E1-=J*kronecker[j][spin[neigh[site][k]]];
}
E2 += exp(-E1/(KB*_TEMP));
}
Assim obtemos um melhor desempenho computacional, já que não temos uma grande quantidade de "if"" no código. Também utilizamos de forma mais clara a delta de kronecker do nosso hamiltoniano.
Função de Visualização
Podemos estar interessados em ver a evolução do nosso sistema. Podemos plotar diretamente do programa sem gerar os dados e plotar depois. Definimos essa função da forma
void visualize(int *spin)
{
int i;
printf("unset xtics\nunset ytics\n");
printf("set size square\n");
printf("set xrange [0:%d]\nset yrange [0:%d]\n",L-1,L-1);
printf("pl '-' matrix w image\n");
for(i=L2-1; i>=0; i--)
{
printf("%d ", spin[i]);
if(i%L == 0)
{
printf("\n");
}
}
printf("e\n\n");
}
onde a função recebe o sitio. Utilizando um "pipe" redirecionamos a saida diretamente para a o gnuplot. Podemos também não querer plotar sempre, assim definimos uma diretiva que responde a compilação do programa
#ifdef VIEW
if(mcs % 10 == 0)
{
printf("set title 'T = %d MCS'\n", mcs);
visualize(spin);
}
#endif
Assim, se na linha de compilação tiver a opção
-DVIEW
o programa irá, a cada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10 mcs} , plotar a configuração do sistema. Essa opção as vezes se torna importante para visualizar se nosso sistema esta evoluindo da forma que estamos esperando.
Programas Utilizados
Programas na linguagem C. Para utilizar os programas, abra o terminal e compile da forma
$ gcc prog.c -lm
Onde prog.c é o programa que deseja utilizar. É necessário que o programa e a biblioteca com funções para simulações de Monte Carlo estejam no mesmo diretório no momento da compilação. Execute da seguinte maneira
$ ./a.out Q TEMP
onde o segundo termo é o estado Q do sistema e o terceiro é a temperatura do sistema. Os programas possuem uma diretiva de compilação para visualização do sistema ao decorrer da execução. Para utilizar é necessário ter o gnuplot [4] instalado e compilar da forma
$ gcc -DVIEW prog.c -lm
e então executar da maneira
$ ./a.out Q TEMP | gnuplot
Entretanto com a visualização no gnuplot o programa demora mais para executar, então é recomendado diminuir os tempos de transiente (TRAN) e medidas (TMAX) caso se queira observar a simulação inteira.
O script possui alguns exemplos de execução através de diferentes estados e temperaturas do sistema. Copie o conteudo em um arquivo e então o deixar executável:
$ chmod +x script.sh
e então com o programa compilado pode executar da forma
$ ./script.sh
Biblioteca com funções em C para simulações de Monte Carlo
Script em bash para gerar os dados
Referências
- ↑ 1,0 1,1 F. Y. Wu, The Potts Model, Rev. Mod. Phys. 54, 235, 1982
- ↑ M. E. J. Newman, G. T. Barkema, "Monte Carlo Methods in Statistical Physics". Oxford University Press Inc., New York, 1999.
- ↑ 3,0 3,1 3,2 Gerard Barkema, Jan de Boer, Numerical Study of Phase Transitions in Potts Models, 1991
- ↑ https://fiscomp.if.ufrgs.br/index.php/Gnuplot