DM: um primeiro programa: mudanças entre as edições
Sem resumo de edição |
|||
| (7 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 204: | Linha 204: | ||
</pre> | </pre> | ||
Como a aceleração resultante sobre uma partícula é a soma de todas as forças que agem sobre ela, para cada | Como a aceleração resultante sobre uma partícula é a soma de todas as forças que agem sobre ela, para cada uma delas teríamos que fazer um loop sobre todas as outras, porém, pela Terceira Lei de Newton <math> F_{ij}=-F_{ji} </math>, ou seja, apenas temos que somar sobre todas as combinações de pares de partículas. No primeiro loop abaixo varremos <math> i </math> para todas partículas, no segundo, a varredura começa em <math> i+1 </math> e segue até <math> N-1 </math>. Desse modo, asseguramos que todos os pares de partículas entrem no cálculo, no caso, temos <math> N(N-1)/2 </math> pares. <math> x_1 </math> e <math> x_2 </math> são, respectivamente, as posições das partículas <math> i </math> e <math> j </math>, enquanto <math> dx </math> e <math> dy </math> as distâncias entre elas. Porém, como nosso sistema possui condições periódicas de contorno, nenhum par de partículas poderá ter um distância maior que <math> L/2 </math> em uma dada direção, além disso, elas não precisam necessariamente estar limitadas aos contornos da caixa as quais foram inseridas, mas o cálculo da força sim. Desse modo, a função resto fmod(dx,Lx) nos assegura que nenhuma distância estará fora da caixa. No próximo passo, a função rint(dx/Lx) arredondará o valor da divisão para o inteiro mais próximo, assim, se <math> dx/L_x > 0.5 </math> descontaremos <math> L_x </math> de <math> dx </math> e se <math> dx/L_x \le 0.5 </math> já teremos o <math> dx </math> correto. O mesmo procedimento também é aplicado sobre a componente <math> y </math>. No ''if'' testamos se a distância ao quadrado entre um par de partículas é menor que o raio crítico de interação, ou seja, a distância máxima acima da qual desconsideramos a força entre duas partículas, lembrando que isso é feito devido ao fato do potencial Lennard-Jones ser de curto alcance. | ||
<pre> | <pre> | ||
Edição atual tal como às 18h36min de 16 de setembro de 2015
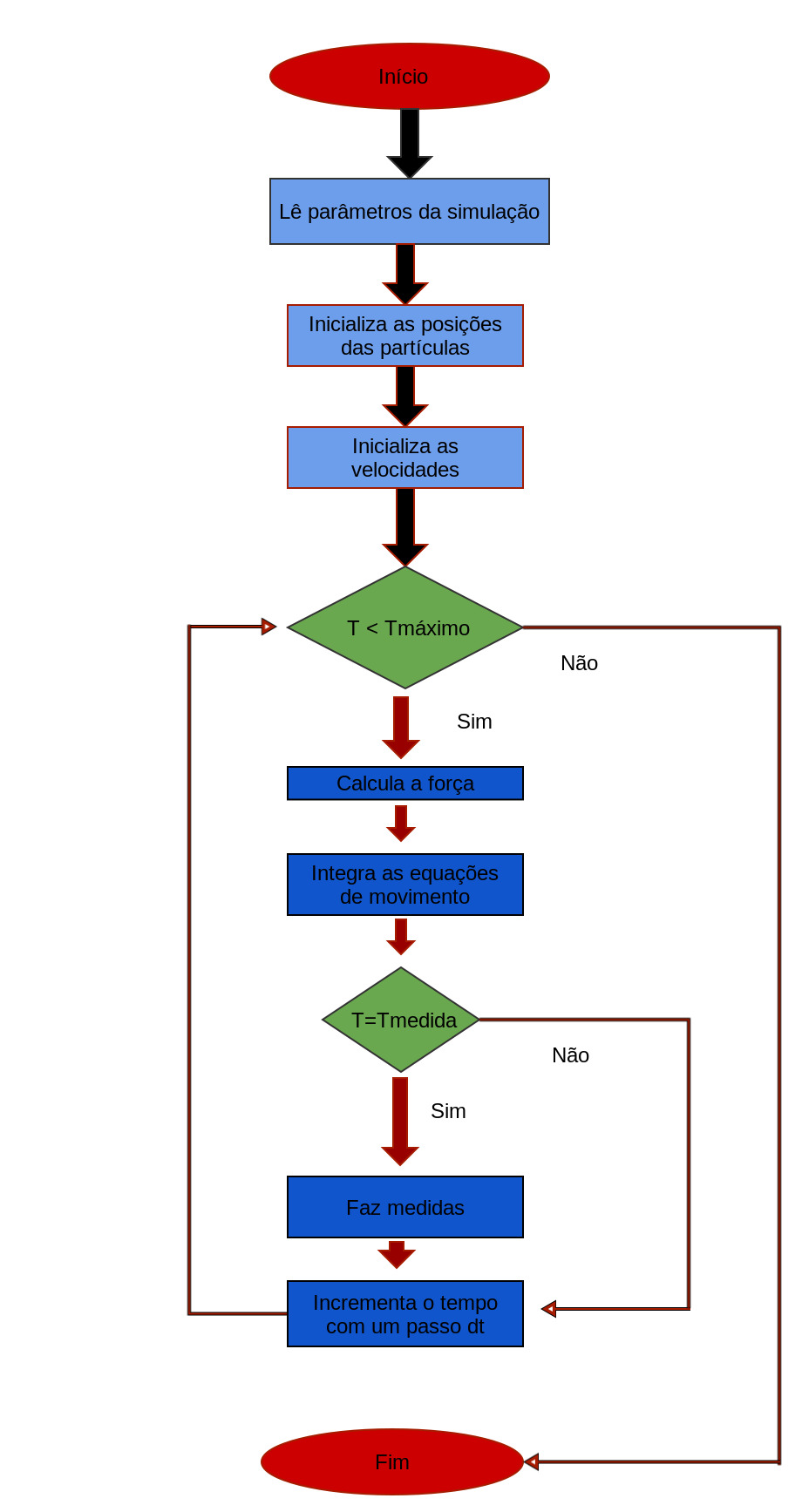
[EM CONSTRUÇÃO] Aqui mostraremos o passo a passo de como montar o primeiro programa para simulação de dinâmica molecular. A linguagem de programação utilizada será o C. Como um primeiro esboço, o programa pode ser organizado como mostra o fluxograma abaixo. Posteriormente, introduziremos partes do código comentando cada etapa. Para o leitor mais familiarizado com DM, ao final da página há o programa completo sem comentários.
A ideia básica da simulação pode ser entendida como: Leitura dos parâmetros da simulação, inicialização das posições das partículas, inicialização das velocidades das partículas, laço temporal onde se calcula a força, integra-se as equações de movimento e, de tempos em tempos, medidas são realizadas.
Abaixo introduzimos partes do código onde começamos declarando as bibliotecas standard utilizadas do C
#include<stdio.h> #include<stdlib.h> #include<math.h>
Está parte é reservada para declarações de constantes que definem os parâmetros da simulação. As constantes podem ser definidas utilizando-se das diretivas de compilação do C através do comando "#define" ou podem ser lidas a partir de um arquivo externo chamado pelo programa. A vantagem do segundo método é que o programa só precisará ser compilado uma única vez para diferentes condições iniciais. Porém, por simplicidade e clareza, optaremos pelo primeiro caso.
#define Nx 16 #define Ny 16 #define Np (Nx*Ny) #define Lx 16 #define Ly 16 #define Rc 4 #define Rc2 (Rc*Rc) #define T 1. #define dt 0.01 #define transient 5. #define total_time 10. #define measure 0.1 #define samples ((total_time-transient)/measure)
representam, respectivamente, o número de partículas nas direções .
representam, respectivamente, o tamanho da rede nas direções .
número total de partículas
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dt } define o intervalo de tempo de integração na simulação.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_c } é o raio de corte acima do qual o cálculo da força é desconsiderado.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle total\_time } é o tempo absoluto da simulação.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle transient } é o tempo que esperamos até o sistema supostamente equilibrar e, então, começarmos a fazer medidas.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle measure } define o intervalo de tempo entre as medições.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle samples } nos dá o número total de medidas que serão realizadas
Conforme o programa é construído, novas constantes podem eventualmente aparecer à medida que novas funções são implementadas. Abaixo declaramos as funções essenciais ao programa, onde cada uma delas será detalhadamente explicada no decorrer da implementação.
void initialize_positions(double *xx, double *yy ) ; void initialize_velocities(double *vx, double *vy ) ; void compute_forces( double *ffx, double *ffy, double *xx, double *yy, double *eenergia ) ; void integrate_EqMotion( double *fx, double *fy, double *xx, double *yy, double *xxp, double *yyp, double eenergia, double *energy_pp, double *vxm ) ;
A seguir introduzimos a função principal
void main(void)
{
FILE *file1,*file2;
file1=fopen("energy.dat","w");
file2=fopen("trajectories.dat","w");
unsigned i;
double *x,*y,*xo,*yo,*vx,*vy,*Fx,*Fy,Ep,Ec,Vxm=0.,t;
size_t size=N*sizeof(double);
x= (double*)malloc(size);
y= (double*)malloc(size);
xo=(double*)malloc(size);
yo=(double*)malloc(size);
vx=(double*)malloc(size);
vy=(double*)malloc(size);
Fx=(double*)malloc(size);
Fy=(double*)malloc(size);
Acima são declaradas todas as variáveis essenciais ao programa, assim como a alocação de memória para os vetores como posição, velocidade, força, etc. Com os vetores alocados, podemos agora inicializar as velocidades e posições das partículas na rede
initialize_velocities(vx,vy); initialize_positions(x,y,xo,yo,vx,vy);
Abaixo é mostrada a parte principal do programa, o loop sobre o tempo. A cada passo de tempo, a rotina Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle compute\_forces } calcula a força e a energia potencial das partículas a partir de suas posições, na sequência, a rotina Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle integrate\_EqMotion } atualiza as posições das partículas. O Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle for } em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } imprime no arquivo "trajectories.dat" as posições e velocidades de todas as partículas no instante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t } . No Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle if } testamos se o tempo total é maior que o tempo de equilíbrio e se a medida deve ser feita, caso seja, no arquivo "energy.dat" imprimiremos, respectivamente, o tempo, energia cinética, energia potencial e a energia total.
for(t=0.;t<total_time;t+=dt)
{
compute_forces(Fx,Fy,x,y,&Ep);
integrate_EqMotion(Fx,Fy,x,y,xo,yo,&Ec,&Vxm);
for(i=0;i<N;i++)fprintf(file2,"%lf %lf %lf %lf\n",x[i],y[i],vx[i],vy[i]);
fflush(file2);
rewind(file2);
if( t>transient && (1.-fmod(t/measure,1.) )<0.00001 )
{
fprintf(file1,"%lf %lf %lf %lf\n",t,Ec,Ep,Ec+Ep);
fflush(file1);
}
}
fclose(file1);
fclose(file2);
free(x);
free(y);
free(xo);
free(yo);
free(vx);
free(vy);
free(Fx);
free(Fy);
}
Agora descrevemos detalhadamente todas as rotinas que aparecem na parte principal. Começamos com a inicialização das velocidades, a rotina recebe os ponteiros das velocidades nas direções Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y } . Como condição inicial, todas as partículas recebem uma velocidade aleatória dada por rand()/RAND_MAX que gera um número entre zero e um. Vcx e Vcy são, respectivamente, as componentes da velocidade do centro de massa do sistema nas direções Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y } , enquanto V2 é a energia cinética. Para o caso em que as partículas estejam transladando em uma direção preferencial, descontamos suas velocidades pela do centro de massa, além disso, as renormalizamos por um fator de escala que depende da temperatura inicial dada, lembrando que a mesma pode variar no ensamble microcanônico.
void initialize_velocities(double *vx,double *vy)
{
unsigned i;
double Vcx=0.,Vcy=0.,V2=0.,fs;
for(i=0;i<N;i++)
{
vx[i]=1.*rand()/RAND_MAX;
vy[i]=1.*rand()/RAND_MAX;
Vcx+=vx[i];
Vcy+=vy[i];
V2 +=vx[i]*vx[i] + vy[i]*vy[i];
}
Vcx/=N;
Vcy/=N;
V2 /=N;
fs=sqrt(2.*T/V2);
for(i=0;i<N;i++)
{
vx[i]=(vx[i]-Vcx)*fs;
vy[i]=(vy[i]-Vcy)*fs;
}
}
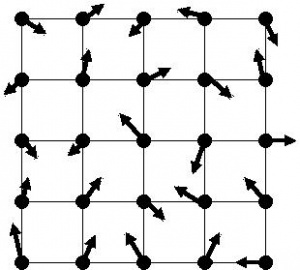
A rotina da inicialização das posições recebe os ponteiros das coordenadas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y } das partículas, as coordenadas no tempo anterior Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0 } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_0 } , além das velocidades inicias Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_x } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_y } . Podemos imaginar a disposição inicial das partículas como uma rede quadrada representada na Figura 2, onde em cada vértice se encontra uma partícula, a distância entre elas é dada por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dx=L_x/N_x } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dy=L_y/N_y } . Como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } é o índice global das partículas, o resto (%) da divisão inteira entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_x } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Nx } nos dará a coordenada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x } , enquanto o resultado da divisão inteira entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_y } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ny } definirá a coordenada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y } .
void initialize_positions(double *x,double *y,double *xo,double *yo,double *vx,double *vy)
{
unsigned i;
double dx,dy;
dx=(double)Lx/Nx;
dy=(double)Ly/Ny;
for(i=0;i<N;i++)
{
x[i]=(i%Nx)*dx;
y[i]=(i/Ny)*dy;
xo[i]=x[i]-vx[i]*dt;
yo[i]=y[i]-vy[i]*dt;
}
}
O cálculo da força é a parte mais crucial do programa, pois é a que mais consome recursos e pode ser drasticamente melhorada com otimizações. Abaixo introduzimos a rotina mais simples possível para o cálculo da força. Ela recebe os ponteiros das forças nas direções Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y } , as coordenadas (o potencial Lennard-Jones só depende da posição) e a energia potencial. No primeiro loop zeramos as duas componentes da força para todas as partículas.
void compute_forces(double *fx,double *fy,double *x,double *y,double *Ep)
{
unsigned i,j;
double x1,y1,x2,y2,dx,dy,r2,r2i,r6,ff,Energy=0.;
for(i=0;i<N;i++)
{
fx[i] = 0.;
fy[i] = 0.;
}
Como a aceleração resultante sobre uma partícula é a soma de todas as forças que agem sobre ela, para cada uma delas teríamos que fazer um loop sobre todas as outras, porém, pela Terceira Lei de Newton Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_{ij}=-F_{ji} } , ou seja, apenas temos que somar sobre todas as combinações de pares de partículas. No primeiro loop abaixo varremos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } para todas partículas, no segundo, a varredura começa em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i+1 } e segue até Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N-1 } . Desse modo, asseguramos que todos os pares de partículas entrem no cálculo, no caso, temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N(N-1)/2 } pares. Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1 } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2 } são, respectivamente, as posições das partículas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j } , enquanto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dx } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dy } as distâncias entre elas. Porém, como nosso sistema possui condições periódicas de contorno, nenhum par de partículas poderá ter um distância maior que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L/2 } em uma dada direção, além disso, elas não precisam necessariamente estar limitadas aos contornos da caixa as quais foram inseridas, mas o cálculo da força sim. Desse modo, a função resto fmod(dx,Lx) nos assegura que nenhuma distância estará fora da caixa. No próximo passo, a função rint(dx/Lx) arredondará o valor da divisão para o inteiro mais próximo, assim, se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dx/L_x > 0.5 } descontaremos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_x } de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dx } e se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dx/L_x \le 0.5 } já teremos o Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dx } correto. O mesmo procedimento também é aplicado sobre a componente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y } . No if testamos se a distância ao quadrado entre um par de partículas é menor que o raio crítico de interação, ou seja, a distância máxima acima da qual desconsideramos a força entre duas partículas, lembrando que isso é feito devido ao fato do potencial Lennard-Jones ser de curto alcance.
for(i=0;i<N;i++)
{
x1=x[i]; y1=y[i];
for(j=i+1;j<N;j++)
{
x2=x[j];
dx=x1 - x2;
dx=fmod(dx,Lx);
dx=dx-rint(dx/Lx)*Lx;
y2=y[j];
dy=y1 - y2;
dy=fmod(dy,Ly);
dy=dy-rint(dy/Ly)*Ly;
r2=dx*dx + dy*dy;
if(r2<Rc2)
{
r2i=1/r2 ;
r6=r2i*r2i*r2i;
ff=48*r2i*r6*(r6-0.5);
fx[i] += ff*dx; fy[i] += ff*dy;
fx[j] -= ff*dx; fy[j] -= ff*dy;
Energy += 4*r6*(r6-1);
}
}
}
*Ep=Energy;
}