Gás de Rede 2D: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| (69 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
Este trabalho tem o intuito de apresentar uma descrição do modelo do Gás de Rede bidimensional e traçar paralelos com o modelo de Ising, discutindo a relação entre seus Hamiltonianos. | |||
== Gás de Rede == | == Gás de Rede == | ||
| Linha 5: | Linha 6: | ||
O Modelo do Gás de Rede 2D consiste em um sistema de <math>N</math> partículas da forma <math>\sigma = {\sigma_1, \sigma_1, \dotsc, \sigma_N}</math> onde cada sítio da rede pode assumir o valor <math>1</math>, ocupado por uma partícula, ou <math>0</math>, não ocupado por uma partícula. A energia total do sistema é dada pelo Hamiltoniano do Gás de Rede, descrito pela equação | O Modelo do Gás de Rede 2D consiste em um sistema de <math>N</math> partículas da forma <math>\sigma = {\sigma_1, \sigma_1, \dotsc, \sigma_N}</math> onde cada sítio da rede pode assumir o valor <math>1</math>, ocupado por uma partícula, ou <math>0</math>, não ocupado por uma partícula. A energia total do sistema é dada pelo Hamiltoniano do Gás de Rede, descrito pela equação | ||
<math>\mathcal{H} = - \epsilon \sum_{\langle i,j \rangle} \sigma_i \sigma_j</math> | <math>\mathcal{H} = - \epsilon \sum_{\langle i,j \rangle} \sigma_i \sigma_j \qquad (1)</math>, | ||
onde o somatório é dado entre os quatro vizinhos mais próximos e <math>\epsilon</math> é a constante de interação entre as partículas, para <math>\epsilon \geq 0</math> a interação é atrativa. Por se tratar de uma rede quadrada com <math>L^2 = L \times L</math> sítios, apenas uma parcela da rede é ocupada por partículas, ou seja, possuímos uma densidade constante <math>\rho</math> de partículas. Podemos expressar a condição da densidade constante da forma | |||
<math>\ | <math>\sum_{i} \sigma_i = \rho L^2</math> | ||
Fazendo uma mudança de variáveis da forma <math>s_i = 2 \ | Fazendo uma mudança de variáveis da forma <math>s_i = 2 \sigma_i - 1</math> saímos da situação de ocupação e não ocupação de sítios e obtemos variáveis do Modelo de Ising <ref name=ISING> https://fiscomp.if.ufrgs.br/index.php/Ising_2D</ref>, spins Up e Down. A variável <math>s_i</math> assume valor <math>+1</math> (up) quando o sítio esta ocupado por uma partícula e <math>-1</math> quando não está. Aplicando a mudança de variáveis no Hamiltoniano do Gás de Rede obtemos | ||
<math>\mathcal{H} = - \frac{1}{4} \epsilon \sum_{\langle i,j \rangle} (s_i + 1)(s_j + 1)</math> | <math>\mathcal{H} = - \frac{1}{4} \epsilon \sum_{\langle i,j \rangle} (s_i + 1)(s_j + 1)</math> | ||
<math> | <math> = - \frac{1}{4} \epsilon \sum_{\langle i,j \rangle}[s_i s_j + s_i + s_j + 1]</math> | ||
<math> = - \frac{1}{4} \epsilon \sum_{\langle i,j \rangle}s_i s_j - \frac{1}{4} \epsilon \sum_{\langle i,j \rangle}s_i - \frac{1}{4} \epsilon \sum_{\langle i,j \rangle}s_j - \frac{1}{4} \epsilon \sum_{\langle i,j \rangle}1</math>. | |||
== | Abrindo os termos dos três últimos somatórios se encontra que | ||
<math> \sum_{\langle i,j \rangle}s_i = \sum_{\langle i,j \rangle}s_j = z \sum_{i}s_i</math>, e | |||
<math> \sum_{\langle i,j \rangle} 1 = z L^2</math>, | |||
o que simplifica a expressão para | |||
<math>\mathcal{H} = - \frac{1}{4} \epsilon \sum_{\langle i,j \rangle}s_i s_j - \frac{1}{2} \epsilon z \sum_{i} s_i - \frac{1}{4} \epsilon z L^2 \qquad (2)</math>, | |||
onde <math>z</math> é o número de coordenação, isto é, o número de vizinhos de cada sítio, que para a rede quadrada é 4. Note a mudança no índice do somatório de <math>s_i</math>. Vemos que este Hamiltoniano possui a forma do Hamiltoniano do modelo de Ising com aplicação de um campo magnético externo, a menos de uma constante. Entretanto, com a densidade constante, fazendo a mesma mudança de variáveis, obtemos | |||
<math>\sum_{i} s_i = (2\rho - 1) L^2 \qquad (3)</math>. | |||
Aplicando essa relação no Hamiltoniano obtemos | |||
<math>\mathcal{H} = - \frac{1}{4} \epsilon \sum_{\langle i,j \rangle} s_i s_j - z \epsilon L^2 \rho </math>. | |||
Como <math>z</math>, <math>\rho</math> e <math>L^2</math> são constantes, o segundo termo é constante. Definindo <math>J = \epsilon / 4</math> o Hamiltoniano se torna | |||
<math>\mathcal{H} = - J \sum_{\langle i,j \rangle} s_i s_j + \text{constante}</math>. | |||
A constante não influencia nos valores da medida, pois ela se cancela na equação de mudança de estado <ref name=BARKEMA>M. E. J. Newman, G. T. Barkema, "Monte Carlo Methods in Statistical Physics". Oxford University Press Inc., New York, 1999.</ref>. Vemos que, ao assumir a densidade constante, o modelo do Gás de Rede se torna o modelo de Ising sem a presença de um campo magnético. A condição da densidade constante é a magnetização total do modelo. | |||
É interessante notar que podemos tratar o modelo do gás de rede de duas formas: '''(a)''' assumir a densidade constante e utilizar o primeiro Hamiltoniano apresentado, ou '''(b)''' não assumir a densidade constante, aplicar a mudança de variáveis discutida e utilizar o Hamiltoniano que possuí a forma de Ising com campo magnético. | |||
==Método de Monte Carlo== | |||
===Princípios gerais=== | |||
Para desenvolver a dinâmica do gás de rede, isto é, fazer com que ocorram alterações na posição das partículas, recorre-se ao método de Monte Carlo. Trata-se, em linhas gerais, de um método estatístico baseado em amostragem aleatória. É comum, ao introduzir-se o assunto, utilizar problemas de cálculo de áreas, como, por exemplo, a clássica história das crianças que desenharam, na areia, um círculo contido em um quadrado, de modo que o diâmetro do círculo seja igual ao lado do quadrado. Jogam, aleatoriamente, pedras no quadrado. Após uma grande quantidade de arremessos, compara-se o valor de pedras que estão dentro do círculo com o número total dentro do quadrado, fazendo a razão entre esses dois valores, encontra-se uma aproximação para a razão entre a área do círculo e a do quadrado, que equivale a <math>\pi/4</math>. Desse modo, pode ser encontrada uma aproximação do valor de <math>\pi</math> através do método de Monte Carlo, que simula uma aproximação experimental<ref name=KRAUTH>Krauth ,W. ,"Statistical Mechanics: Algorithms and Computations". Oxford Master Series in Physics, Oxford University Press, 2006.</ref>. É possível propor um novo modelo, no qual o quadrado é grande e as pedras são atiradas aleatoriamente de dentro do quadrado, de modo que a posição de arremesso é atualizada para a posição da última pedra jogada. A principal alteração nesse método é a possibilidade de que uma pedra seja atirada para fora do quadrado. Nesse caso, a posição para o próximo arremesso não muda e as pedras que foram parar fora das bordas do quadrado são empilhadas naquela posição. Essas mudanças no método caracterizam a aplicação de Monte Carlo em uma cadeia de Markov, definida de modo que a configuração do próximo estado depende somente da configuração atual. Até aqui, vimos o método de Monte Carlo aplicado em situações nas quais a probabilidade de um evento ocorrer na configuração subsequente do sistema é zero ou um. Para novas distribuições de probabilidade, utiliza-se o algoritmo de Metrópolis. | |||
===Algoritmo de Metrópolis=== | |||
Como mencionado, o método de Monte Carlo funciona através de atualizações em um sistema, fazendo com que ele passe de um estado para outro. Consideremos <math>\mu</math> como sendo o estado atual do sistema. O próximo estado será chamado <math>\nu</math>. Chamamos a probabilidade do sistema passar do estado <math>\mu</math> para o estado <math>\nu</math> de <math>p(\mu\to\nu)</math>. A ideia do algoritmo de Metrópolis é aplicar essa probabilidade no método de Monte Carlo. Para isso, um método muito utilizado é calcular a probabilidade <math>p(\mu\to\nu)</math> e compará-la a um número aleatório <math>r</math>, de modo que <math>0<r<1</math>. Se <math> p(\mu\to\nu)>r</math>, então o estado <math>\nu</math> é adotado pelo sistema. Para aplicar essas ideias ao problema do gás de rede, o método mais simples é utilizando o algoritmo de Kawasaki, que faz com que dois sítios, selecionados aleatoriamente, tenham seus valores trocados. Isso implica que a magnetização do sistema será constante<ref name = BARKEMA></ref>. Para calcular a probabilidade de aceitação dessa mudança, calcula-se a variação de energia entre os estados,<math>\Delta E= E_{\nu}-E_{\mu}</math>, e aplica-se o valor obtido na equação de probabilidade de aceitação de Metrópolis: | |||
<math>p(\mu\to\nu)=\left\{\begin{array}{rc} e^{\frac{-\Delta E}{k_BT}}, \quad \text{se}\quad \Delta E>0\\ | |||
1, \quad \text{caso contrario}\end{array}\right.</math> | |||
Para este trabalho, inicialmente foram feitas algumas alterações no algoritmo de Kawasaki. Limita-se a troca de valores somente entre um sítio e seus quatro vizinhos principais (isto é, acima, abaixo, à direita e à esquerda). Isso porque se tinha a intenção de recriar o comportamento difusivo de um gás no modelo do gás de rede em duas dimensões, porém, essa escolha para a dinâmica das simulações limita em muito a facilidade do sistema equilibrar, como será mostrado na parte de resultados. O algoritmo inicial consiste na seguinte ideia: No estado <math>\mu</math>, seleciona-se aleatoriamente um sítio <math>i</math>. A partir dele, é sorteado um de seus vizinhos, digamos, <math>j</math>, com o qual haverá a troca de valor. Antes que ocorra a troca, são calculados os valores de dois Hamiltonianos: o que relaciona o sítio <math>i</math> com seus vizinhos e o que relaciona <math>j</math> com seus vizinhos. Somados, eles representam o valor de <math>E_{\mu}</math>. Após a troca, esses valores são recalculados, formando o valor de <math>E_{\nu}</math>. Com esses valores, segue-se o cálculo da probabilidade da forma usual. | |||
Após verificar que a dinâmica inicialmente escolhida não era apropriada, optou-se por usar o algoritmo de Kawasaki tradicional, fazendo uso de uma listagem de quais eram os estados dos sítios e escolhendo os pares a serem trocados sempre como sítios de estados diferentes. Isso faz com que a aceitação do algoritmo de Monte Carlo seja muito mais elevada que ao do nosso algoritmo inicial, pois no caso em que grandes clusters são formados as trocas eram sempre rejeitadas de acordo com a dinâmica inicial. | |||
===Considerações práticas=== | |||
Já consideramos os aspectos iniciais do método de Monte Carlo, mostrando suas aplicações. Vimos, do mesmo modo, a utilização do algoritmo de Metrópolis, dentro do qual aplicamos o algoritmo de Kawasaki (modificado) para desenvolver o sistema do gás de rede. Resta elucidar a função do parâmetro temporal, isto é, como as iterações desses algoritmos influenciam o sistema. Primeiramente, deve-se fixar um valor para o número de passos temporais que serão realizados. Em cada passo temporal, são realizadas <math>L^2</math> iterações do algoritmo de Metrópolis, abordado acima, sendo <math>L</math> o lado da rede quadrada. Chamamos de Passo de Monte Carlo (MCS) cada um desses passos temporais. Em outras palavras: em cada passo de Monte Carlo, todos os sítios tem a possibilidade de realizar uma troca. | |||
== Resultados == | == Resultados == | ||
=== Eficiência da dinâmica local === | |||
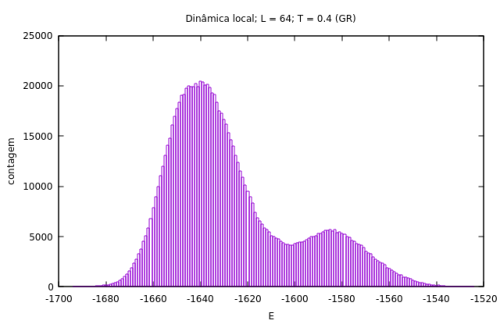
Como mencionado acima, a primeira dinâmica escolhida foi a que restringe os sítios a trocarem de estado para apenas aqueles que são vizinhos próximos (os 4 acima, abaixo, a direita e a esquerda). Se verificou ao analisar os dados das simulações que na verdade essa dinâmica não era apropriada, pois a aceitação do algoritmo é muito baixa e com a amostragem escolhida (<math>10^6</math> MCS) o sistema ainda não estaria equilibrado. Isso pode ser percebido mais facilmente observando os histogramas das simulações. Sabe-se que a distribuição das grandezas macroscópicas de um sistema termodinâmico é a distribuição de Boltzmann <ref name = BARKEMA></ref>, então se espera para o sistema analisado que a energia tenha uma distribuição normal de frequências. Observe a diferença entre as distribuições para a energia do sistema no caso da dinâmica local inicialmente escolhida e no caso do algoritmo tradicional de Kawasaki: | |||
{| class="wikitable" style="text-align: center;" | |||
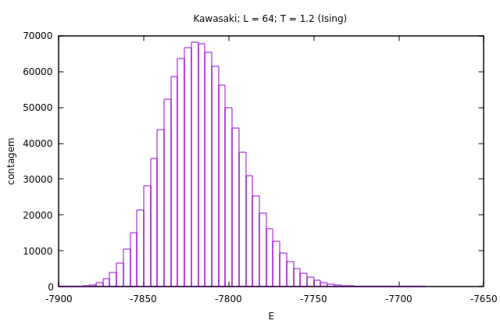
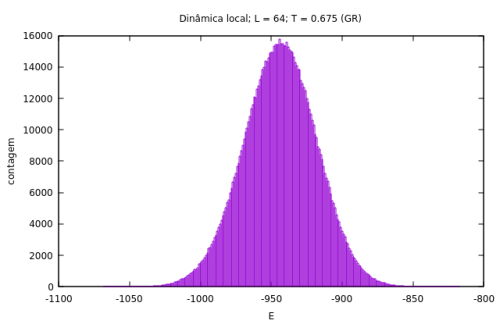
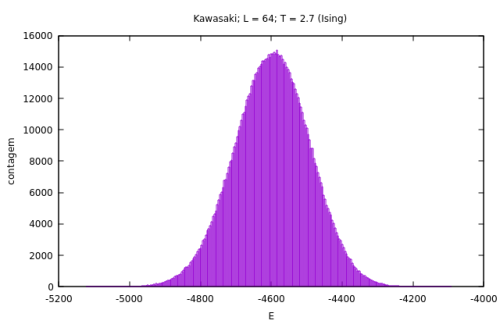
!colspan="2"|Diferença entre distribuições para a energia do sistema por dinâmica escolhida. | |||
|- | |||
|[[Arquivo:hist_dinamica_local.png|thumb|upright=4|none|alt=Alt text|Distribuição da energia para a dinâmica local após <math>10^6</math> MCS.|500px]] | |||
|[[Arquivo:hist_kawasaki.png|thumb|upright=4|none|alt=Alt text|Distribuição da energia para a dinâmica do algoritmo de Kawasaki após <math>10^6</math> MCS.|500px]] | |||
|- | |||
|[[Arquivo:hist_dinamica_local_alta_temp.png|thumb|upright=4|none|alt=Alt text|Distribuição da energia para a dinâmica local em alta temperatura (acima da temperatura crítica) após <math>10^6</math> MCS.|500px]] | |||
|[[Arquivo:hist_kawasaki_alta_temp.png|thumb|upright=4|none|alt=Alt text|Distribuição da energia para a dinâmica do algoritmo de Kawasaki em alta temperatura (acima da temperatura crítica) após <math>10^6</math> MCS.|500px]] | |||
|- | |||
|} | |||
Assim podemos notar que o sistema não está equilibrado após a amostragem com a dinâmica local. No caso do algoritmo tradicional o sistema se encontra em equilíbrio. Para temperaturas mais altas, acima da temperatura crítica para cada modelo onde não há mais separação de fase, a dinâmica tem eficiência satisfatória, pois a aceitação do algoritmo de Monte Carlo é maior já que sem a formação de grandes clusters a probabilidade de uma partícula ser selecionada e poder trocar para um sítio vazio que seja seu vizinho é muito maior. Contudo, ainda assim é mais vantajoso executar as simulações na linguagem de Ising, já que a aceitação do algoritmo ainda é maior do que para a dinâmica local proposta, então a quantidade de dados descorrelacionados para a mesma amostragem de <math>10^6</math> MCS é maior. Dessa maneira, para uma amostragem de mesmo tamanho, o valor estimado para uma grandeza <math>\langle Q \rangle</math> é mais preciso no caso da dinâmica proposta pelo algoritmo de Kawasaki, e para uma mesma precisão no valor estimado seria necessária uma amostragem menor do que a da dinâmica local. | |||
A referência na qual esse trabalho mais se inspira, Monte Carlo Methods in Statistical Physics, de Newman e Barkema, não dá a devida ênfase para quão interessante computacionalmente é se manter na linguagem do modelo de Ising e adotar o algoritmo de Kawasaki. | |||
É importante notar que as simulações da dinâmica de Kawasaki foram feitas na linguagem do modelo de Ising, com spins <math>+1</math> e <math>-1</math>, ao invés de sítios ocupados por partículas <math>1</math> e sítios desocupados <math>0</math>. Essa mudança é importante para entender a mudança na escala das grandezas entre as simulações. Como a constante de interação <math>J</math> do modelo de Ising é um quarto da constante <math>\epsilon</math>, a temperatura e a energia no modelo de Ising valem <math>\frac{1}{4}</math> da temperatura e da energia nas simulações com a dinâmica local na linguagem do gás de rede. | |||
=== Separação de fases === | |||
{| class="wikitable" style="text-align: center;" | |||
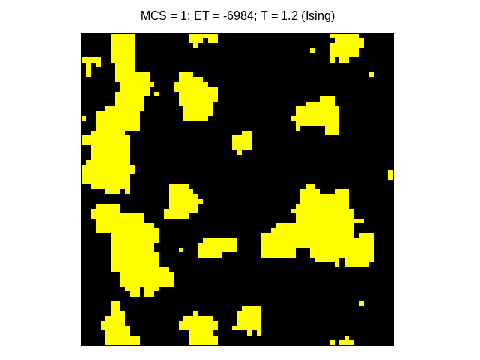
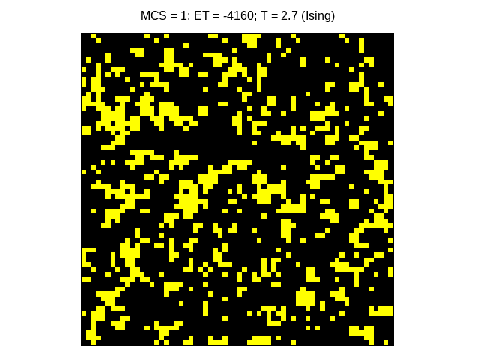
!colspan="2"|Animações ilustrando as duas fases acima e abaixo de <math>T_c = 0.56725</math>. | |||
|- | |||
|[[Arquivo:sep_fases.gif|thumb|center|none|alt=Alt text|Separação de fases do sistema do gás de rede em fases de densidade alta e baixa. Note como ocorre a formação de clusters e estes tendem a se agrupar formando clusters ainda maiores.|480px]] | |||
|[[Arquivo:gas.gif|thumb|center|none|alt=Alt text|Fase gasosa do modelo do gás de rede com densidade constante. Note como os clusters se agrupam e se desfazem rapidamente.|480px]] | |||
|- | |||
|} | |||
Um dos aspectos interessantes do modelo do gás de rede é o fato de ser um modelo chamado de COP-Ising, ou Ising com parâmetro de ordem conservado. O fato de a densidade ser constante no modelo do gás de rede implica que o modelo de Ising análogo tem a magnetização constante (chamado de parâmetro de ordem). Abaixo da temperatura crítica <math>T_c = 0.56725</math> o sistema se separa em duas fases com densidades diferentes, se acomodando na forma de clusters cada vez maiores conforme a temperatura diminui. Acima de <math>T_c</math> o sistema assume uma forma "gasosa", em que a formação de pequenos clusters é apenas momentânea e a densidade sobre a rede é aproximadamente homogênea. | |||
=== Energia e efeito do tamanho da rede === | |||
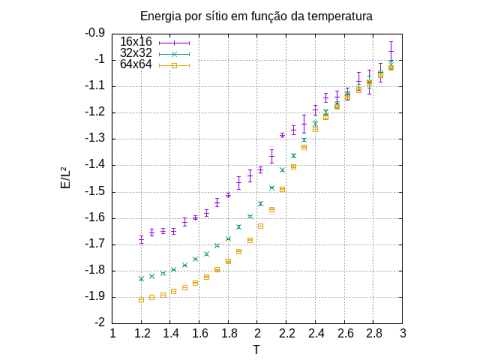
A grandeza que foi medida nas simulações é a energia total do sistema. Para analisar os efeitos do tamanho da rede devemos comparar os valores das energias por número de sítios, já que quanto maior a rede maior o número de partículas e portanto maior o valor absoluto da energia. Abaixo temos um gráfico com os valores da energia total do sistema por número de sítios em função da temperatura, com os dados das três redes simuladas (L = 16, 32, 64). | |||
[[Arquivo:energia.png|thumb|center|none|alt=Alt text|Energia total do sistema dividida pelo número de sítios em função da temperatura para redes de tamanhos diferentes. Cada ponto no gráfico é a média de 5 amostragens com seu desvio padrão.|480px]] | |||
Aqui o comportamento da energia é como esperado para o modelo. Há uma queda no valor da energia conforme a temperatura do reservatório diminui abaixo da temperatura crítica, e conforme a temperatura aumenta acima da temperatura crítica, a energia aumenta mais devagar dado que é o estado em que o sistema está na sua fase amorfa. | |||
Algo que se nota no gráfico acima é a diferença nos valores da energia das redes <math>L = 32</math> e <math>L = 64</math> e a rede de <math>L = 16</math>. É perceptível que as duas redes maiores apresentam valores de energia muito mais próximos. Isso se dá justamente pelo tamanho da rede e o fato da densidade ser a mesma. | |||
{| class="wikitable" style="text-align: center;" | |||
!colspan="2"|Ilustração dos estados de menor energia | |||
|- | |||
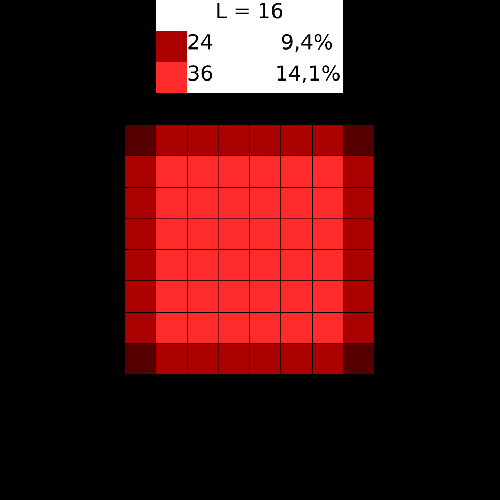
|[[Arquivo:rede16.png|thumb|center|upright=4|none|alt= Alt text|Diagrama ilustrando o estado de menor energia para a rede de <math>L = 16</math>. As cores indicam o número de sítios vizinhos ocupados.|480px]] | |||
|[[Arquivo:diagrama.gif|thumb|upright=4|none|alt=Alt text|Animação ilustrando o número de partículas internas ao cluster se tornando mais relevante que o número de partículas nas bordas conforme a rede aumenta.|500px]] | |||
|- | |||
|} | |||
Para entender como o valor da energia total do sistema por número de sítios varia com o tamanho da rede é interessante calcular essa grandeza no estado de menor energia. No caso da rede quadrada, o estado de menor energia é um cluster quadrado. Como ilustrado no diagrama acima, existem sítios com 3 vizinhos ocupados e sítios com 2 vizinhos ocupados. Estes são os da borda do cluster. Todos os outros internos ao cluster tem 4 vizinhos ocupados e portanto contribuem com <math>-4\epsilon</math> para o Hamiltoniano. | |||
Nesse trabalho adotamos <math>\rho = 0.25</math>, o que facilita o cálculo da energia total, pois o tamanho do lado do cluster é <math> l = \sqrt{\frac{L^2}{4}}</math>. Temos <math>(l - 2)^2</math> partículas internas ao cluster e portanto com 4 vizinhos e <math>4(l - 2)</math> partículas nas bordas com 3 vizinhos. O Hamiltoniano é portanto | |||
<math>\mathcal{H}_{GR} = (-2\epsilon)4 + (-3\epsilon)4(l - 2) + (-4\epsilon)(l - 2)^2</math>. | |||
O primeiro termo é a referente às interações dos 4 cantos do cluster, que tem apenas 2 vizinhos ocupados. Abrindo os termos e simplificando a equação chegamos ao valor do Hamiltoniano do estado de menor energia do gás de rede: | |||
<math>\mathcal{H}_{GR} = -(L^2 - 2L)\epsilon</math>. | |||
Dividindo por 2 para encontrar o valor da energia total e então por <math>L^2</math> chegamos em | |||
<math>e = \frac{E}{L^2} = - \frac{\epsilon}{2} + \frac{\epsilon}{L}</math>, | |||
que é a grandeza apresentada no gráfico anterior. Essa elaboração foi feita para o modelo do gás de rede, porém as simulações foram feitas com o modelo de Ising, com a restrição de que a magnetização era constante (a quantidade de spins <math>+1</math> e <math>-1</math> é constante). | |||
Usando a equação <math>(2)</math> e <math>J = \frac{\epsilon}{4}</math> chegamos em | |||
<math>\mathcal{H}_{ising} = -J\sum_{\langle i, j \rangle}s_i s_j - 8J\sum{i}s_i - 4JL^2</math>. | |||
Utilizamos então a equação <math>(3)</math> e <math>\rho = 0.25</math> e percebemos que os termos do meio e da direita se cancelam, deixando somente o primeiro termo para avaliarmos em termos do estado de menor energia. | |||
<math>\mathcal{H}_{ising} = -J\sum_{\langle i, j \rangle}s_i s_j - 8J(2\rho - 1)L^2 - 4JL^2 </math> | |||
<math> = -J\sum_{\langle i, j \rangle}s_i s_j </math> | |||
Agora podemos avaliar o Hamiltoniano do estado de menor energia do modelo de Ising nessas condições. Para isso podemos nos basear no diagrama usado anteriormente, com a ressalva de que os sítios imediatamente fora do cluster também interagem com ele, já que temos agora spins <math>-1</math> ao invés de sítios vazios. Temos o mesmo número de spins internos ao cluster que de pariculas anteriormente, assim como para as bordas do cluster e os mesmos quatro cantos. Além disso, os sítios fora do cluster também tem contribuição para o Hamiltoniano. O número de spins fora do cluster com 4 vizinhos <math>-1</math> é <math>L^2 - \frac{L^2}{4} - 2L</math> e o número de spins fora do cluster com 1 vizinho <math>+1</math> é <math>2L</math>. Agora podemos somar todas essas contribuições. | |||
<math>\mathcal{H}_{ising} = (-4J)(L^2 - \frac{L^2}{4} - 2L) + (-2J)(2L) + (-2J)4(\frac{L}{2} - 2) + (-4J)(\frac{L}{2} - 2)^2 </math> | |||
Da esquerda para a direita os termos são a contribuição dos spins fora do cluster com 4 vizinhos <math>-1</math>, dos spins fora do cluster mas com um vizinho no cluster, dos spins na borda do cluster e dos spins interiores ao cluster. Abrindo os termos e simplificando a equação chegamos finalmente em | |||
<math>\mathcal{H}_{ising} = -(4L^2 - 8L)J</math> | |||
E como nas simulações foram utilizadas que <math>\epsilon = 1</math> para o caso do gás de rede e <math>J = 1</math> para o modelo de Ising, temos portanto que as energias medidas com o modelo de Ising são equivalentes a 4 vezes as energias no modelo do gás de rede, como se verificou ao implementar a mesma função de medida para a linguagem de spins e de sítios vazios e ocupados. E com essa equação para o Hamiltoniano do estado de menor energia do modelo de Ising nessas condições podemos perceber que o efeito do tamanho de rede é praticamente o mesmo, com a ressalva de que a energia por sítio deve ser também 4 vezes a energia por sítio do modelo do gás de rede. | |||
== Conclusão == | |||
Passamos pelo que vem a ser o modelo do gás de rede na rede quadrada e apresentamos sua relação com o modelo de Ising. O Hamiltoniano do modelo do gás de rede nos mostra que ele é idêntico ao modelo de Ising com um termo de campo magnético externo. Ao fixarmos a densidade do modelo do gás de rede, impomos a restrição de que o modelo de Ising deve ter a magnetização constante para mantermos a equivalência. Também se discutiu o efeito do tamanho das redes simuladas e vimos que quanto maior o tamanho da rede mais próximo será o valor das energias por sítio em comparação com redes de tamanhos similares e vimos que isso se deve pelo fato do número de sítios no cluster do estado de menor energia crescer mais rápido no interior do cluster do que em seu perímetro. | |||
== Programas Utilizados == | == Programas Utilizados == | ||
Programas na linguagem C. Para utilizar os programas, abra o terminal e compile da forma | |||
<source lang=sh> | |||
$ gcc prog.c -lm | |||
</source> | |||
Onde ''prog.c'' é o programa que deseja utilizar. E execute da seguinte maneira | |||
<source lang=sh> | |||
$ ./a.out TEMP SEED | |||
</source> | |||
onde o segundo termo é a temperatura do banho térmico e o terceiro é a semente utilizada pelo gerador de números pseudo-aleatórios. Os programas possuem uma diretiva de compilação para visualização do sistema ao decorrer da execução. Para utilizar é necessário ter o gnuplot <ref name=GNUPLOT>https://fiscomp.if.ufrgs.br/index.php/Gnuplot</ref> instalado e compilar da forma | |||
<source lang=sh> | |||
$ gcc -DGNU prog.c -lm | |||
</source> | |||
e então executar da maneira | |||
<source lang=sh> | |||
$ ./a.out TEMP SEED | gnuplot | |||
</source> | |||
Entretanto com a visualização no gnuplot o programa pode demorar mais para executar, então é recomendado diminuir os tempos de transiente (''TRAN'') e medidas (''TMAX''). | |||
[[Gás de Rede com Densidade Constante e dinâmica local]] | |||
[[Modelo de ising com magnetização constante e algoritmo de Kawasaki]] | |||
[[Biblioteca com funções em C para simulações de Monte Carlo]] | |||
== Referências == | == Referências == | ||
<references/> | <references/> | ||
Edição atual tal como às 05h42min de 27 de novembro de 2020
Este trabalho tem o intuito de apresentar uma descrição do modelo do Gás de Rede bidimensional e traçar paralelos com o modelo de Ising, discutindo a relação entre seus Hamiltonianos.
Gás de Rede
O Modelo do Gás de Rede 2D consiste em um sistema de partículas da forma onde cada sítio da rede pode assumir o valor , ocupado por uma partícula, ou , não ocupado por uma partícula. A energia total do sistema é dada pelo Hamiltoniano do Gás de Rede, descrito pela equação
,
onde o somatório é dado entre os quatro vizinhos mais próximos e é a constante de interação entre as partículas, para a interação é atrativa. Por se tratar de uma rede quadrada com sítios, apenas uma parcela da rede é ocupada por partículas, ou seja, possuímos uma densidade constante de partículas. Podemos expressar a condição da densidade constante da forma
Fazendo uma mudança de variáveis da forma saímos da situação de ocupação e não ocupação de sítios e obtemos variáveis do Modelo de Ising [1], spins Up e Down. A variável assume valor (up) quando o sítio esta ocupado por uma partícula e quando não está. Aplicando a mudança de variáveis no Hamiltoniano do Gás de Rede obtemos
.
Abrindo os termos dos três últimos somatórios se encontra que
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\langle i,j \rangle}s_i = \sum_{\langle i,j \rangle}s_j = z \sum_{i}s_i} , e
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\langle i,j \rangle} 1 = z L^2} ,
o que simplifica a expressão para
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} = - \frac{1}{4} \epsilon \sum_{\langle i,j \rangle}s_i s_j - \frac{1}{2} \epsilon z \sum_{i} s_i - \frac{1}{4} \epsilon z L^2 \qquad (2)} ,
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} é o número de coordenação, isto é, o número de vizinhos de cada sítio, que para a rede quadrada é 4. Note a mudança no índice do somatório de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_i} . Vemos que este Hamiltoniano possui a forma do Hamiltoniano do modelo de Ising com aplicação de um campo magnético externo, a menos de uma constante. Entretanto, com a densidade constante, fazendo a mesma mudança de variáveis, obtemos
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i} s_i = (2\rho - 1) L^2 \qquad (3)} .
Aplicando essa relação no Hamiltoniano obtemos
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} = - \frac{1}{4} \epsilon \sum_{\langle i,j \rangle} s_i s_j - z \epsilon L^2 \rho } .
Como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2} são constantes, o segundo termo é constante. Definindo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J = \epsilon / 4} o Hamiltoniano se torna
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} = - J \sum_{\langle i,j \rangle} s_i s_j + \text{constante}} .
A constante não influencia nos valores da medida, pois ela se cancela na equação de mudança de estado [2]. Vemos que, ao assumir a densidade constante, o modelo do Gás de Rede se torna o modelo de Ising sem a presença de um campo magnético. A condição da densidade constante é a magnetização total do modelo.
É interessante notar que podemos tratar o modelo do gás de rede de duas formas: (a) assumir a densidade constante e utilizar o primeiro Hamiltoniano apresentado, ou (b) não assumir a densidade constante, aplicar a mudança de variáveis discutida e utilizar o Hamiltoniano que possuí a forma de Ising com campo magnético.
Método de Monte Carlo
Princípios gerais
Para desenvolver a dinâmica do gás de rede, isto é, fazer com que ocorram alterações na posição das partículas, recorre-se ao método de Monte Carlo. Trata-se, em linhas gerais, de um método estatístico baseado em amostragem aleatória. É comum, ao introduzir-se o assunto, utilizar problemas de cálculo de áreas, como, por exemplo, a clássica história das crianças que desenharam, na areia, um círculo contido em um quadrado, de modo que o diâmetro do círculo seja igual ao lado do quadrado. Jogam, aleatoriamente, pedras no quadrado. Após uma grande quantidade de arremessos, compara-se o valor de pedras que estão dentro do círculo com o número total dentro do quadrado, fazendo a razão entre esses dois valores, encontra-se uma aproximação para a razão entre a área do círculo e a do quadrado, que equivale a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi/4} . Desse modo, pode ser encontrada uma aproximação do valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} através do método de Monte Carlo, que simula uma aproximação experimental[3]. É possível propor um novo modelo, no qual o quadrado é grande e as pedras são atiradas aleatoriamente de dentro do quadrado, de modo que a posição de arremesso é atualizada para a posição da última pedra jogada. A principal alteração nesse método é a possibilidade de que uma pedra seja atirada para fora do quadrado. Nesse caso, a posição para o próximo arremesso não muda e as pedras que foram parar fora das bordas do quadrado são empilhadas naquela posição. Essas mudanças no método caracterizam a aplicação de Monte Carlo em uma cadeia de Markov, definida de modo que a configuração do próximo estado depende somente da configuração atual. Até aqui, vimos o método de Monte Carlo aplicado em situações nas quais a probabilidade de um evento ocorrer na configuração subsequente do sistema é zero ou um. Para novas distribuições de probabilidade, utiliza-se o algoritmo de Metrópolis.
Algoritmo de Metrópolis
Como mencionado, o método de Monte Carlo funciona através de atualizações em um sistema, fazendo com que ele passe de um estado para outro. Consideremos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} como sendo o estado atual do sistema. O próximo estado será chamado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} . Chamamos a probabilidade do sistema passar do estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} para o estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(\mu\to\nu)} . A ideia do algoritmo de Metrópolis é aplicar essa probabilidade no método de Monte Carlo. Para isso, um método muito utilizado é calcular a probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(\mu\to\nu)} e compará-la a um número aleatório Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} , de modo que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0<r<1} . Se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(\mu\to\nu)>r} , então o estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} é adotado pelo sistema. Para aplicar essas ideias ao problema do gás de rede, o método mais simples é utilizando o algoritmo de Kawasaki, que faz com que dois sítios, selecionados aleatoriamente, tenham seus valores trocados. Isso implica que a magnetização do sistema será constante[2]. Para calcular a probabilidade de aceitação dessa mudança, calcula-se a variação de energia entre os estados,Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta E= E_{\nu}-E_{\mu}} , e aplica-se o valor obtido na equação de probabilidade de aceitação de Metrópolis:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(\mu\to\nu)=\left\{\begin{array}{rc} e^{\frac{-\Delta E}{k_BT}}, \quad \text{se}\quad \Delta E>0\\ 1, \quad \text{caso contrario}\end{array}\right.}
Para este trabalho, inicialmente foram feitas algumas alterações no algoritmo de Kawasaki. Limita-se a troca de valores somente entre um sítio e seus quatro vizinhos principais (isto é, acima, abaixo, à direita e à esquerda). Isso porque se tinha a intenção de recriar o comportamento difusivo de um gás no modelo do gás de rede em duas dimensões, porém, essa escolha para a dinâmica das simulações limita em muito a facilidade do sistema equilibrar, como será mostrado na parte de resultados. O algoritmo inicial consiste na seguinte ideia: No estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} , seleciona-se aleatoriamente um sítio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} . A partir dele, é sorteado um de seus vizinhos, digamos, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} , com o qual haverá a troca de valor. Antes que ocorra a troca, são calculados os valores de dois Hamiltonianos: o que relaciona o sítio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} com seus vizinhos e o que relaciona Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} com seus vizinhos. Somados, eles representam o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\mu}} . Após a troca, esses valores são recalculados, formando o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\nu}} . Com esses valores, segue-se o cálculo da probabilidade da forma usual.
Após verificar que a dinâmica inicialmente escolhida não era apropriada, optou-se por usar o algoritmo de Kawasaki tradicional, fazendo uso de uma listagem de quais eram os estados dos sítios e escolhendo os pares a serem trocados sempre como sítios de estados diferentes. Isso faz com que a aceitação do algoritmo de Monte Carlo seja muito mais elevada que ao do nosso algoritmo inicial, pois no caso em que grandes clusters são formados as trocas eram sempre rejeitadas de acordo com a dinâmica inicial.
Considerações práticas
Já consideramos os aspectos iniciais do método de Monte Carlo, mostrando suas aplicações. Vimos, do mesmo modo, a utilização do algoritmo de Metrópolis, dentro do qual aplicamos o algoritmo de Kawasaki (modificado) para desenvolver o sistema do gás de rede. Resta elucidar a função do parâmetro temporal, isto é, como as iterações desses algoritmos influenciam o sistema. Primeiramente, deve-se fixar um valor para o número de passos temporais que serão realizados. Em cada passo temporal, são realizadas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2} iterações do algoritmo de Metrópolis, abordado acima, sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} o lado da rede quadrada. Chamamos de Passo de Monte Carlo (MCS) cada um desses passos temporais. Em outras palavras: em cada passo de Monte Carlo, todos os sítios tem a possibilidade de realizar uma troca.
Resultados
Eficiência da dinâmica local
Como mencionado acima, a primeira dinâmica escolhida foi a que restringe os sítios a trocarem de estado para apenas aqueles que são vizinhos próximos (os 4 acima, abaixo, a direita e a esquerda). Se verificou ao analisar os dados das simulações que na verdade essa dinâmica não era apropriada, pois a aceitação do algoritmo é muito baixa e com a amostragem escolhida (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^6} MCS) o sistema ainda não estaria equilibrado. Isso pode ser percebido mais facilmente observando os histogramas das simulações. Sabe-se que a distribuição das grandezas macroscópicas de um sistema termodinâmico é a distribuição de Boltzmann [2], então se espera para o sistema analisado que a energia tenha uma distribuição normal de frequências. Observe a diferença entre as distribuições para a energia do sistema no caso da dinâmica local inicialmente escolhida e no caso do algoritmo tradicional de Kawasaki:
Assim podemos notar que o sistema não está equilibrado após a amostragem com a dinâmica local. No caso do algoritmo tradicional o sistema se encontra em equilíbrio. Para temperaturas mais altas, acima da temperatura crítica para cada modelo onde não há mais separação de fase, a dinâmica tem eficiência satisfatória, pois a aceitação do algoritmo de Monte Carlo é maior já que sem a formação de grandes clusters a probabilidade de uma partícula ser selecionada e poder trocar para um sítio vazio que seja seu vizinho é muito maior. Contudo, ainda assim é mais vantajoso executar as simulações na linguagem de Ising, já que a aceitação do algoritmo ainda é maior do que para a dinâmica local proposta, então a quantidade de dados descorrelacionados para a mesma amostragem de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^6} MCS é maior. Dessa maneira, para uma amostragem de mesmo tamanho, o valor estimado para uma grandeza Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle Q \rangle} é mais preciso no caso da dinâmica proposta pelo algoritmo de Kawasaki, e para uma mesma precisão no valor estimado seria necessária uma amostragem menor do que a da dinâmica local. A referência na qual esse trabalho mais se inspira, Monte Carlo Methods in Statistical Physics, de Newman e Barkema, não dá a devida ênfase para quão interessante computacionalmente é se manter na linguagem do modelo de Ising e adotar o algoritmo de Kawasaki. É importante notar que as simulações da dinâmica de Kawasaki foram feitas na linguagem do modelo de Ising, com spins Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle +1} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1} , ao invés de sítios ocupados por partículas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} e sítios desocupados Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} . Essa mudança é importante para entender a mudança na escala das grandezas entre as simulações. Como a constante de interação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J} do modelo de Ising é um quarto da constante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} , a temperatura e a energia no modelo de Ising valem Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} da temperatura e da energia nas simulações com a dinâmica local na linguagem do gás de rede.
Separação de fases
| Animações ilustrando as duas fases acima e abaixo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c = 0.56725} . | |
|---|---|
Um dos aspectos interessantes do modelo do gás de rede é o fato de ser um modelo chamado de COP-Ising, ou Ising com parâmetro de ordem conservado. O fato de a densidade ser constante no modelo do gás de rede implica que o modelo de Ising análogo tem a magnetização constante (chamado de parâmetro de ordem). Abaixo da temperatura crítica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c = 0.56725} o sistema se separa em duas fases com densidades diferentes, se acomodando na forma de clusters cada vez maiores conforme a temperatura diminui. Acima de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} o sistema assume uma forma "gasosa", em que a formação de pequenos clusters é apenas momentânea e a densidade sobre a rede é aproximadamente homogênea.
Energia e efeito do tamanho da rede
A grandeza que foi medida nas simulações é a energia total do sistema. Para analisar os efeitos do tamanho da rede devemos comparar os valores das energias por número de sítios, já que quanto maior a rede maior o número de partículas e portanto maior o valor absoluto da energia. Abaixo temos um gráfico com os valores da energia total do sistema por número de sítios em função da temperatura, com os dados das três redes simuladas (L = 16, 32, 64).
Aqui o comportamento da energia é como esperado para o modelo. Há uma queda no valor da energia conforme a temperatura do reservatório diminui abaixo da temperatura crítica, e conforme a temperatura aumenta acima da temperatura crítica, a energia aumenta mais devagar dado que é o estado em que o sistema está na sua fase amorfa.
Algo que se nota no gráfico acima é a diferença nos valores da energia das redes Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = 32} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = 64} e a rede de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = 16} . É perceptível que as duas redes maiores apresentam valores de energia muito mais próximos. Isso se dá justamente pelo tamanho da rede e o fato da densidade ser a mesma.
Para entender como o valor da energia total do sistema por número de sítios varia com o tamanho da rede é interessante calcular essa grandeza no estado de menor energia. No caso da rede quadrada, o estado de menor energia é um cluster quadrado. Como ilustrado no diagrama acima, existem sítios com 3 vizinhos ocupados e sítios com 2 vizinhos ocupados. Estes são os da borda do cluster. Todos os outros internos ao cluster tem 4 vizinhos ocupados e portanto contribuem com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -4\epsilon} para o Hamiltoniano.
Nesse trabalho adotamos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = 0.25} , o que facilita o cálculo da energia total, pois o tamanho do lado do cluster é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle l = \sqrt{\frac{L^2}{4}}} . Temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (l - 2)^2} partículas internas ao cluster e portanto com 4 vizinhos e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4(l - 2)} partículas nas bordas com 3 vizinhos. O Hamiltoniano é portanto
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{GR} = (-2\epsilon)4 + (-3\epsilon)4(l - 2) + (-4\epsilon)(l - 2)^2} .
O primeiro termo é a referente às interações dos 4 cantos do cluster, que tem apenas 2 vizinhos ocupados. Abrindo os termos e simplificando a equação chegamos ao valor do Hamiltoniano do estado de menor energia do gás de rede:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{GR} = -(L^2 - 2L)\epsilon} .
Dividindo por 2 para encontrar o valor da energia total e então por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2} chegamos em
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle e = \frac{E}{L^2} = - \frac{\epsilon}{2} + \frac{\epsilon}{L}} ,
que é a grandeza apresentada no gráfico anterior. Essa elaboração foi feita para o modelo do gás de rede, porém as simulações foram feitas com o modelo de Ising, com a restrição de que a magnetização era constante (a quantidade de spins Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle +1} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1} é constante).
Usando a equação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (2)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J = \frac{\epsilon}{4}} chegamos em
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{ising} = -J\sum_{\langle i, j \rangle}s_i s_j - 8J\sum{i}s_i - 4JL^2} .
Utilizamos então a equação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (3)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = 0.25} e percebemos que os termos do meio e da direita se cancelam, deixando somente o primeiro termo para avaliarmos em termos do estado de menor energia.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{ising} = -J\sum_{\langle i, j \rangle}s_i s_j - 8J(2\rho - 1)L^2 - 4JL^2 } Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle = -J\sum_{\langle i, j \rangle}s_i s_j }
Agora podemos avaliar o Hamiltoniano do estado de menor energia do modelo de Ising nessas condições. Para isso podemos nos basear no diagrama usado anteriormente, com a ressalva de que os sítios imediatamente fora do cluster também interagem com ele, já que temos agora spins Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1} ao invés de sítios vazios. Temos o mesmo número de spins internos ao cluster que de pariculas anteriormente, assim como para as bordas do cluster e os mesmos quatro cantos. Além disso, os sítios fora do cluster também tem contribuição para o Hamiltoniano. O número de spins fora do cluster com 4 vizinhos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1} é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2 - \frac{L^2}{4} - 2L} e o número de spins fora do cluster com 1 vizinho Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle +1} é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2L} . Agora podemos somar todas essas contribuições.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{ising} = (-4J)(L^2 - \frac{L^2}{4} - 2L) + (-2J)(2L) + (-2J)4(\frac{L}{2} - 2) + (-4J)(\frac{L}{2} - 2)^2 }
Da esquerda para a direita os termos são a contribuição dos spins fora do cluster com 4 vizinhos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1} , dos spins fora do cluster mas com um vizinho no cluster, dos spins na borda do cluster e dos spins interiores ao cluster. Abrindo os termos e simplificando a equação chegamos finalmente em
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{ising} = -(4L^2 - 8L)J}
E como nas simulações foram utilizadas que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon = 1} para o caso do gás de rede e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J = 1} para o modelo de Ising, temos portanto que as energias medidas com o modelo de Ising são equivalentes a 4 vezes as energias no modelo do gás de rede, como se verificou ao implementar a mesma função de medida para a linguagem de spins e de sítios vazios e ocupados. E com essa equação para o Hamiltoniano do estado de menor energia do modelo de Ising nessas condições podemos perceber que o efeito do tamanho de rede é praticamente o mesmo, com a ressalva de que a energia por sítio deve ser também 4 vezes a energia por sítio do modelo do gás de rede.
Conclusão
Passamos pelo que vem a ser o modelo do gás de rede na rede quadrada e apresentamos sua relação com o modelo de Ising. O Hamiltoniano do modelo do gás de rede nos mostra que ele é idêntico ao modelo de Ising com um termo de campo magnético externo. Ao fixarmos a densidade do modelo do gás de rede, impomos a restrição de que o modelo de Ising deve ter a magnetização constante para mantermos a equivalência. Também se discutiu o efeito do tamanho das redes simuladas e vimos que quanto maior o tamanho da rede mais próximo será o valor das energias por sítio em comparação com redes de tamanhos similares e vimos que isso se deve pelo fato do número de sítios no cluster do estado de menor energia crescer mais rápido no interior do cluster do que em seu perímetro.
Programas Utilizados
Programas na linguagem C. Para utilizar os programas, abra o terminal e compile da forma
$ gcc prog.c -lm
Onde prog.c é o programa que deseja utilizar. E execute da seguinte maneira
$ ./a.out TEMP SEED
onde o segundo termo é a temperatura do banho térmico e o terceiro é a semente utilizada pelo gerador de números pseudo-aleatórios. Os programas possuem uma diretiva de compilação para visualização do sistema ao decorrer da execução. Para utilizar é necessário ter o gnuplot [4] instalado e compilar da forma
$ gcc -DGNU prog.c -lm
e então executar da maneira
$ ./a.out TEMP SEED | gnuplot
Entretanto com a visualização no gnuplot o programa pode demorar mais para executar, então é recomendado diminuir os tempos de transiente (TRAN) e medidas (TMAX).
Gás de Rede com Densidade Constante e dinâmica local
Modelo de ising com magnetização constante e algoritmo de Kawasaki
Biblioteca com funções em C para simulações de Monte Carlo
Referências
- ↑ https://fiscomp.if.ufrgs.br/index.php/Ising_2D
- ↑ 2,0 2,1 2,2 M. E. J. Newman, G. T. Barkema, "Monte Carlo Methods in Statistical Physics". Oxford University Press Inc., New York, 1999.
- ↑ Krauth ,W. ,"Statistical Mechanics: Algorithms and Computations". Oxford Master Series in Physics, Oxford University Press, 2006.
- ↑ https://fiscomp.if.ufrgs.br/index.php/Gnuplot















![{\displaystyle =-{\frac {1}{4}}\epsilon \sum _{\langle i,j\rangle }[s_{i}s_{j}+s_{i}+s_{j}+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14d9c1fb0c677fde12c35be55882892e2bb6662b)