BOIDS: mudanças entre as edições

De Física Computacional
Ir para navegação Ir para pesquisar
(Criou página com 'Alunos: Ben-Hur Cardoso e Vinícius Garcia O potencial devido a interação entre duas partículas separadas por uma distância <math>r'</math> pode ser modelado pelo potenc...')
 
Sem resumo de edição
 
Linha 1: Linha 1:
Alunos: Ben-Hur Cardoso e Vinícius Garcia
Alunos: Álvaro Essinger, Pedro Widniczck.
=Contexto Histórico=
Desenvolvido por Craig Reynolds, engenheiro de software, em 1986, é um algoritmo que busca, por meio de regras básicas, reproduzir o comportamento sincronizado de grupos de animais. Por exemplo manadas de animais terrestres, cardumes de peixes, bando de pássaros e etc. O nome BOID corresponde ao encurtamento da expressão em inglês ''“bird-oid object”'', que se refere a um objeto “tipo pássaro”. Seu trabalho foi publicado em 87 sob o título original, em inglês, ''"Flocks, herds and schools: A distributed behavioral model"''.
O modelo base de Craig já fora utilizado para diversas implementações e estudos. Como estudo comportamental de medo, interação entre animais via olfato modelando feromônios, mudança de liderança de um bando, dentre muitas outras aplicações interessantes.


Posteriormente, em 1995, Tamás Vicsek, cientista húngaro, apresentou um modelo simplificado de BOID para o estudo de transições de fase de um sistema desordenado para um estado ordenado de larga escala. Esse tipo de transição espontânea é um exemplo de movimento coletivo. Esse modelo é bastante popular atualmente na área da física.


O potencial devido a interação entre duas partículas separadas por uma distância <math>r'</math> pode ser modelado pelo potencial de Lennard-Jones <ref>Lennard-Jones, J. E. (1924), "On the Determination of Molecular Fields", Proc. R. Soc. Lond. A, 106 (738): 463–477</ref>:
=Motivação=
O movimento de animais em sincronia é extremamente complexo e é chave para sua sobrevivência em bando. Peixes, pássaros e mamíferos terrestres tem esse tipo de comportamento principalmente no que diz respeito a defesa em momentos em que sentem em perigo. A concentração intimida e o movimento confunde seus predadores. Além de ser extremamente prazeroso assistir um bando de pássaros ou um cardume de peixes em sua dança sincronizada.


<math>U'(r') = 4 \epsilon \left [ \left ( \frac{\sigma}{r'} \right )^{12} - \left ( \frac{\sigma}{r'} \right )^{6} \right ]</math>
Este trabalho busca, em suas etapas, reproduzir um cardume de peixes em seu padrão síncrono de movimento e, posteriormente, na presença de um ou mais predadores.


Posto em unidades reduzidas (<math>r \equiv r'/ \sigma</math> e <math>U \equiv U' / \epsilon</math>), o potencial reduz-se a: 


<math>U(r) = 4  \left [ \left ( \frac{1}{r} \right )^{12} - \left ( \frac{1}{r} \right )^{6} \right ]</math>
= O Algoritmo Para BOIDS =
Inicialmente são sorteadas posições e velocidades aleatórias para os objetos. As regras são então calculadas a cada de passo temporal. Embora cada boid tenha liberdade sobre todo o espaço descrito, o seu comportamento é influenciado apenas por outros dentro de uma região circular centrada no objeto dita ''raio de interação'' (R). Após o cálculo das novas posições e velocidades é somado um incremento de tempo e o algoritmo recomeça.


[[Arquivo:LennardJones.png|500px|center]]
== Separação ==
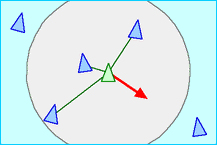
Interação de repulsão entre os indivíduos para evitar superconcentração local (ou no caso extremo uma superposição). Uma força central, dependente apenas da distância entre o boid e a origem da força:


As quantidades físicas de interesse (como pressão, tempo e temperatura) possuem ordens de grandeza muito diferentes entre si quando se usa unidades do Sistema Internacional, o que faz com que fique difícil de identificar erros. Por causa disso, é computacionalmente viável trabalhar com o seguintes sistema de unidades básicas, que mantém os valores em baixas ordens de grandeza:
<math>\vec{V}_j = \frac{S (\vec{r}_j - \vec{r}_k)}{||\vec{r}||^2}</math>, onde <math>\vec{r} = (x_j-x_k)\hat{i} + (y_j-y_k)\hat{j}</math> e <math>S</math> é o coeficiente de separação.


{| class="wikitable"
[[Arquivo:Rule_separation.gif|thumb|none|300px|Fig1. link:https://en.wikipedia.org/wiki/Boids#/media/File:Rule_separation.gif]]
|-
! '''Grandeza'''
! '''Comprimento'''
! '''Tempo'''
! '''Massa'''
! '''Temperatura'''
! '''Energia'''
! '''Pressão'''
! '''Densidade'''
|-
| '''Unidade'''
| <math>\sigma</math>
| <math>\sigma \sqrt{m_p / \epsilon}</math>
| <math>m_p</math>
| <math>\epsilon/k_B</math>
| <math>\epsilon</math>
| <math>\epsilon / \sigma^3</math>
| <math>1 / \sigma^{3}</math>
|}
onde <math>m_p</math> é a massa da partícula e <math>k_B</math> é a constante de Boltzmann.


Note que as novas unidades são adimensionais. Assim, para comparar o modelo com um sistema físico real, deve-se converter para as unidades desejadas. É interessante notar que a simulação feita utilizando as unidades reduzidas permite visualizar que sistemas distintos serão equivalentes, já que há infinitas combinações de densidade, temperatura, <math>\epsilon </math> e <math>\sigma </math> com mesmas unidades reduzidas.
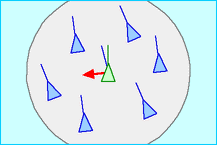
== Alinhamento (vetor velocidade) ==
A velocidade média dos parceiros próximos influencia o vetor velocidade do objeto, fazendo-o ter um comportamento parecido com sua vizinhança.


== Método Monte Carlo ==
<math>\vec{V}^{n+1}_{j} = \frac{1}{k} \Sigma^{k}_{i=1} \vec{V}_{i}</math>, com <math>k</math> sendo o número de vizinhos dentro do raio de interação.


Denomina-se método de Monte Carlo métodos estatísticos que se baseiam em amostragem aleatória massiva para cálculo numérico.
[[Arquivo:Rule_alignment.gif|thumb|none|300px|Fig2. link:https://en.wikipedia.org/wiki/Boids#/media/File:Rule_alignment.gif]]


=== Amostragem simples ===
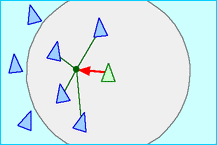
== Coesão ==  
Os BOIDs interagentes tem um potencial de mola entre si, fazendo com que tenham a tendência de mover-se em direção ao centro de massa do grupo. Calculando primeiramente o centro de massa (CM) das partículas vizinhas utiliza-se da força elástica para simular uma mola entre o objeto e o CM da vizinhança.


O cálculo numérico de uma integral utilizando Monte Carlo parte da ideia de que uma integral pode ser reescrita como:
<math>\vec{r}_{CM} = \frac{1}{N}\Sigma^N_{i=1} \vec{r}_i</math>,  com <math>N</math> sendo o número de partículas dentro do raio de interação.


<math> F = \int_a^b{f(x) dx} = (b - a)\langle f(x) \rangle </math>
<math>\vec{V}_j = C (\vec{r}_j - \vec{r}_{CM})</math>, e <math>C</math> sendo o coeficiente elástico.


Dessa forma, utiliza-se amostragem aleatória massiva para estimar <math> \langle f(x) \rangle </math>, que é a média da função no intervalo de interesse. O estimador para a média real é a média amostral, que por ser uma medida estatística terá sempre um erro inerente associado.


=== Amostragem por importância ===
[[Arquivo:Rule_cohesion.gif|thumb|none|300px|Fig3. link:https://en.wikipedia.org/wiki/Boids#/media/File:Rule_cohesion.gif]]


Um problema da amostragem simples é que ela utiliza uma distribuição uniforme, que pode, para uma função que tenha regiões onde seu valor é próximo de zero por exemplo, custar a estimar corretamente o valor médio da função. A fim de contornar isso, podemos utilizar uma distribuição <math> w(x) </math> tal que a razão <math> \frac{f(x)}{w(x)} </math> seja o mais constante possível. Reescrevendo a integral:
== Ruído ==
Para reproduzir melhor um ser vivo, um pequeno ruído compõe a velocidade. Isso faz com que tenhamos uma maior flutuação no caminho que os boids traçam.


<math> F = \int_a^b{\frac{f(x)}{w(x)} w(x) dx} = (b - a)\left \langle \frac{f(x)}{w(x)} \right \rangle </math>
sendo <math>\zeta</math> um número real aleatório,


<math>V_x = \cos{(\zeta)} V_x - \sin{(\zeta)} V_y</math>, na componente x


Basicamente, é a média dos valores da função razão <math> \frac{f(x)}{w(x)} </math> com distribuição <math> w(x) </math> para sorteio dos pontos. Esse método diminui a variância amostral e faz com que seja muito mais eficiente a convergência do estimador média amostral para a média real da função.
e


=== Algoritmo de Metropolis–Hastings ===
<math>V_y = \sin{(\zeta)} V_x + \cos{(\zeta)} V_y</math>, na componente y.


Dado uma amostra com <math>N</math> partículas, a abordagem introduzida por Metropolis (em 1953, algoritmo para distribuições simétricas) e Hastings (em 1970, algoritmo generalizado) segue o seguinte esquema:
==BOIDS Adaptados Para Cardume de Peixes==


(1) Selecionar uma partícula aleatóriamente, e calcular sua energia <math>U(r)</math>;
Para a realização da adaptação, utiliza-se outra regra de alinhamento, fazendo uma média ponderada entre a velocidade do boid no tempo t com a velocidade dos vizinhos, da forma:
(2) Dado o deslocamento <math>\mathbf{r_n} = \mathbf{r} + \mathbf{\Delta}</math>, calcular <math>U(r_n)</math>;
(3) Aceitar o movimento <math>\mathbf{r} \rightarrow \mathbf{r_n}</math> com probabilidade <math>p = min\{1; \exp[-\beta (U(r_n) - U(r))]\}</math>


Devido ao fato das componentes de <math>\mathbf{\Delta}</math> poderem assumir valores postivos e negativos (com a nova posição limitada por alguma condição de contorno), após ser aceito a mudança de posição de uma dada partícula, elá poderá ser selecionada (no próximo passo) com a mesma probabilidade e voltar a sua posição original. Isso garante a condição de balanço detalhado. <ref> Daan Frenkel, Berend Smit, "Understanding molecular simulation: from algorithms to applications"</ref>
<math>\vec{V}^{n+1}_{j} =  (1-M) v_{j} +  \frac{M}{k} \Sigma^{k}_{i=1} \vec{V}_{i}</math>, M sendo o termo da média.


=== Estimadores no Equilíbrio ===
as outras relaçoes, separação e coesão continuam idênticas. Porém também serão acrescentadas uma barreira repulsiva que dificulte a chegada dos boids na fronteira, sendo a constante de proporcionalidade e E o raio de interação da barreira, da seguinte forma:
Em todos os exemplos tratados aqui, será usado o ensemble NVT (com o número de partículas, volume e temperatura constantes) com <math>d</math> dimensões. Dado isso, os sistemas são caracterizados com um densidade e uma temperatura. Com tais sistemas no equilíbrio, são estimadas (média de sucessivas medidas) a energia total e a pressão, dadas respectivamente por:
<math>U_T = \sum_i \sum_{j>i}U(r_{ij}) </math>


<math>P = \frac{\rho}{\beta} + \frac{2\rho}{Nd}\sum_i \sum_{j>i}\mathbf{f(\mathbf{r_{ij}})} \cdot \mathbf{r_{ij}} </math>
<math> v_{j} = a exp(-(\frac{x_{j} - L}{E})^2) </math>,  para quando o boid se aproxima da extremidade superior do dominio, idem para componente x,


onde <math>\mathbf{r_{ij}} = \mathbf{r_{j}} - \mathbf{r_{i}}</math>. Além disso, é interessante a análise da capacidade térmica
<math> v_{j} = a exp(-(\frac{x_{j}}{E})^2) </math>, para quando o boid se aproxima da parte inferior do dominio. Idem para componente x,


<math>C_v = \frac{\langle U_T^2 \rangle - \langle U_T \rangle ^2}{k_BT^2}</math>
para todos os programas se L = 100, então E = 10 e para L = 1000 então E = 50.


A função radial de distribuição de pares, é uma função que estima o quão provável é encontrar duas partículas a uma distância <math>r</math> dentro de um sistema de várias partículas. Em um sistema de <math>N</math> partículas, o <math>g(r)</math> é definido como a média do número de partículas a uma distância <math>r</math>:
Também é feito que, para todos os boids que possuem mais de <math>0.2N</math> vizinhos, sejam freiados, pois foi observado que peixes quando na presença de vizinhos (semelhantes) diminuem suas velocidades.


<math> g(r)=\frac{1}{N\rho}\langle\sum_{i=1}^N\sum_{j\neq i}^N\delta(r-|r_i-r_j|)  \rangle</math>
== Predador ==
A partícula que representa o predador é uma barreira repulsiva. Obedecendo a


A distribuição de densidades é calculada dividindo espacialmente o sistema, no nosso caso de lado <math> L </math>, em <math> M </math> células de lado <math> \frac{L}{M} </math> e acumular em um histograma as densidades das células. Essa medida é relevante para identificação de fases no sistema.
<math> F_{b} = B \frac{r_{j} - b_{k}}{ ||r_{j} - b_{k}||^{1.5} }  </math>, onde B é o coeficiente da barreira e b é a posição do k-ésimo predador.


== Detalhes Técnicos==
No presente trabalho o predador não persegue os BOIDs, apenas se desloca em linha reta no plano com velocidade constante.


=== Condições de Contorno ===
Aqui[https://youtu.be/mgg6HhKRwY0?t=41] é possível ver o comportamento de um cardume de peixes na presença de algumas arraias.


Qualquer sistema possível de ser feito hoje com método Monte Carlo, apesar do grande poder computacional disponível, fica distante do limite termodinâmico. As condições de contorno podem ser estabelecidas de forma a tentar contornar isso. As condições utilizadas neste trabalho foram condições de contorno periódicas, que possibilitam que o sistema se comporte como se fosse muito maior do que é, desde que ele seja isotrópico.
=Resultados e Discussão=
Nosso modelo foi simulado com condições de contorno periódicas em áreas quadradas de lados <math>L = 1000</math> e <math>L = 100</math>. Abaixo apresentamos os resultados para cada regra isoladamente e ao final todas funcionando simultaneamente com e sem a presença do predador.


=== Convenção da imagem mínima ===
== Separação ==
Aqui temos, como esperado, um comportamento semelhante ao de um gás ideal. Que busca um estado de menor energia ocupando todo o espaço disponível. Note que poucas regiões tem mais de 3 objetos próximos.


Construindo um sistema cúbico de lado L, com um número N de partículas fixo, as condições de contorno periódicas fazem com a simulação não se limite ao cubo. Ao calcular a interação entre duas partículas, portanto, a distância entre elas não é unívoca, já que há incontáveis cópias de cada uma, repetindo-se periodicamente. Resolve-se esse problema utilizando-se da convenção da imagem mínima, em que é calculada a interação com a imagem mais próxima das outras.
[[Arquivo:Separacao.gif‎ |thumb|none|500px| Simulação apenas da regra de separação entre BOIDS. ]]


=== Truncamento nas interações ===
A animação abaixo busca ilustrar a dependência do parâmetro <math>S</math> no sistema, aumentando-o progressivamente.


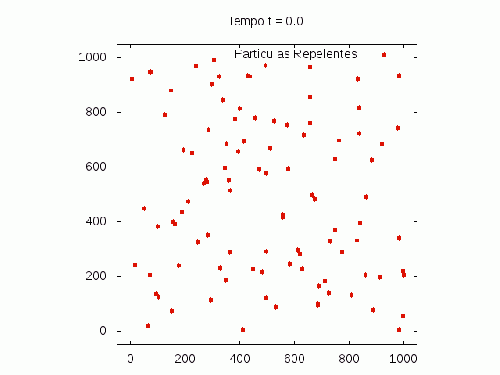
Um problema da condição de contorno periódica é que, a princípio, cada partícula interagiria com todas as outras do sistema, que devido ao fato de ser periodicamente repetido, seriam infinitas. Como o potencial utilizado é de curto alcance, deve ser possível, de alguma forma, limitar as interações entre as partículas sem perda dos significados numéricos da simulação. Pode-se, então, truncar as interações de uma partícula <math> i </math> a partir de uma distância de corte <math> r_c </math> de forma que há uma descontinuidade no potencial dessa partícula na esfera de raio <math> r_c </math>.  
[[Arquivo:Repelentes.gif‎ |thumb|none|500px| Simulação apenas da regra de separação entre BOIDS. ]]


== Coesão ==
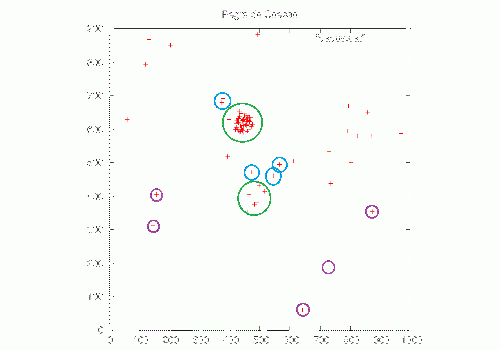
Para a coesão temos um comportamento semelhante ao condensamento de um gás em gotas ou gotículas. As regiões mais concentradas (círculo verde) perdem um pouco de sua capacidade de mobilidade e se tornam atrativas para partículas vizinhas (círculos azuis). Ao passo que objetos isolados (círculos roxos) se comportam independentemente até encontrarem um, ou mais, vizinhos ou regiões de alta concentração.


[[Arquivo: mic.png|300px|center]]
[[Arquivo:Coesao edit.gif |thumb|none|500px| Simulação apenas da regra de coesão entre BOIDS.]]


Na animação abaixo temos o comportamento dinâmico do sistema para o parâmetro <math>C</math> crescente. Note que, de fato, a medida que <math>C</math> aumenta, também ocorre o aumento da concentração dos BOIDs.


Assim o potencial simulado é:
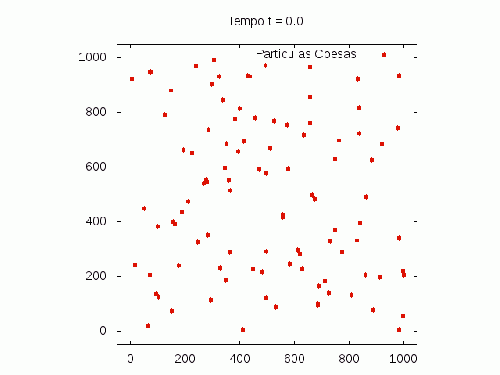
[[Arquivo:Coesas.gif|thumb|none|500px| Simulação apenas da regra de coesão entre BOIDS. ]]


<math> U_{trunc}(r) = \begin{cases}U_{LJ}(r) & , r \leq r_c\\0 & , r > r_c \end{cases}  </math>
== Alinhamento (vetor velocidade) ==
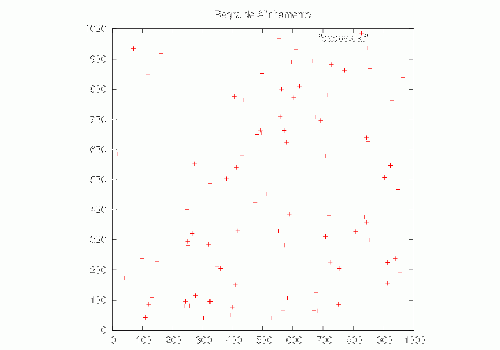
Na regra de alinhamento temos o comportamento do vetor velocidade do objeto sendo influenciado pela velocidade das partículas na vizinhança. Na imagem estática fica difícil de diferenciar da regra de separação, porém, note como aqui há mais regiões com 3 ou mais BOIDs bem próximos. Em alguns casos pode-se notar que quase ocorre uma superposição.


Esse é o chamado truncamento simples. O subíndice LJ se refere ao potencial de Lennard-Jones. O problema é que isso cria uma contribuição indesejada à pressão, já que há uma força de impulso por conta dessa descontinuidade do potencial.
[[Arquivo:Alinhamento 1.gif |thumb|none|500px| Simulação apenas da regra de alinhamento entre BOIDS. ]]


Pode-se, então, usar o truncamento com deslocamento, que evita essa descontinuidade fazendo uma subtração em todo ponto do módulo do potencial de Lennard-Jones à distância <math> r_c </math>. Assim, o potencial simulado é:
A animação abaixo ilustra a influência da regra mostrando o sistema inicialmente com o alinhamento desligado e ligando-o logo após.


<math> U_{deslocado}(r) = \begin{cases}U_{LJ}(r) - U_{LJ}(r_c) & , r \leq r_c\\0 & , r > r_c \end{cases}  </math>
[[Arquivo:Alinhamento.gif‎ |thumb|none|500px| Animação da regra de alinhamento entre BOIDS. ]]


Com esse potencial, que é contínuo, as forças serão sempre finitas, o que retira a força de impulso que alteraria medidas de pressão.
== BOIDS (3 regras ligadas) ==
Aqui temos a implementação das 3 regras básicas ligadas.


=== Translação ===
Os parâmetros usados nessa simulação foram:
<math>C = 0,1 ; S = 0,4</math>, nesse caso não temos o parâmetro <math>M</math> pois só é utilizada a media aritmética das componentes.


A possível nova posição de uma partícula será <math>(x_n, y_n, z_n)</math> tal que
[[Arquivo:BOIDS.gif |thumb|none|500px| Animação BOIDS sem adaptação de cardume. Código:[https://fiscomp.if.ufrgs.br/index.php/Grupo_-_BOIDS/codigo_BOIDS] ]]


  <math> x_n = x + \Delta (\alpha - 0.5)</math>
== BOIDS Adaptados Para Cardume de Peixes ==
  <math> y_n = y + \Delta (\alpha - 0.5)</math>
Implementação das 2 regras básicas de coesão e separação com a modificação da regra de alinhamento buscando um comportamento de grupo mais real. Note que aqui, ao se juntarem, a velocidade diminui. Pois a velocidade está dependo da quantidade de vizinhos.
  <math> z_n = z + \Delta (\alpha - 0.5)</math>


sendo <math>\alpha</math> números aleatórios uniformemente distribuídos e <math> \Delta </math> o deslocamento máximo permitido. Se a nova posição for aceita seguindo o algorítmo de Metropolis, a partícula assumirá essa posição. Caso contrário, a antiga configuração contribuirá novamente na média.  <ref> David P. Landau, Kurt Binder, "A Guide to Monte Carlo Simulations in Statistical Physics"</ref>
Os parâmetros utilizados foram:
<math>C = 0,2; S = 0,3</math>


O tamanho de <math> \Delta </math> não pode ser grande ao ponto de nunca ser aceito nem pequeno ao ponto de sempre ser aceito. Dado isso, buscando uma taxa de aceitação <math> \eta </math> entre <math> 30 \%</math> e <math> 50 \% </math>, define-se um <math> \Delta_0 </math> inicial que vai se ajustando no decorrer da simulação, executando - a cada passo Monte Carlo (<math>N</math> passos de simulação) - o seguinte algorítimo:


  Se (<math> \eta < 0.3 </math>): <math> \Delta \leftarrow \Delta \times (\eta / 0.3)</math> 
[[Arquivo:BoidsMOD.gif |thumb|none|500px| Simulação BOIDS com otimização de velocidade do cardume. Código: [https://fiscomp.if.ufrgs.br/index.php/Grupo_-_BOIDS/codigo_BOIDS_cardume]]]
  Se (<math> \eta > 0.5 </math>): <math> \Delta \leftarrow \Delta \times (\eta / 0.5)</math>


== Sistema bidimensional ==
Para melhorar o comportamento do cardume, fora implementada uma barreira fraca nas bordas da região. Isso fará muita diferença na visualização da situação com predadores.


Dado um sistema com densidade <math> \rho = N / L^2 </math> e temperatura <math>T</math>, os sistemas foram feitos com:
Na situação abaixo foram usados os seguintes parâmetros:
<math>C = 0.05; S =0.3; M=0.15 e B = 0.6</math>


(A) <math> N = 256 </math> partículas
[[Arquivo:Barreiranaborda.gif |thumb|none|500px| Simulação BOIDS com otimização de velocidade do cardume e barreira fraca nas bordas. Código[https://fiscomp.if.ufrgs.br/index.php/Grupo_-_BOIDS/codigo_barreira_fronteira]]]
(B) Quadrado de lado <math> L =  (N / \rho)^{1/2} </math>, utilizando a convenção da imagem mínima
(C) Incialização aleatória
(D) Distância de corte <math>r_c = 2.5 \sigma</math>
(E) Deslocamento máximo inicial <math>\Delta_0 = L/2 </math>
=== Transição de fase líquido-gás ===
A partir do artigo de M Rovere et al <ref> M Rovere et al (1990) "The gas-liquid transition of the two-dimensional Lennard-Jones fluid".  J. Phys.: Condens. Matter 2 7009 </ref>, que modelou o sistema apresentado, obtemos a informação da temperatura e da densidade críticas. Os valores encontrados pelos autores do artigo são <math> T = 0.5</math> e <math> \rho = 0.3 </math>, que determinam qual intervalo de valores de temperatura e densidade apresentam coexistência de fases distintas.


=== Transição de fase com densidade fixa ===
== Predador ==
Resultado obtido com as regras de coesão, separação e alinhamento adaptado para cardume de peixes implementadas. Aqui buscamos colocar os predadores em cena depois de algum tempo dos objetos criados para que o cardume se organize.


Fixada a densidade <math> \rho = 0.3 </math>, foram realizadas simulações para as diferentes temperaturas <math> T \in \{0.45, 0.50, 0.70\}</math>.
Os parâmetros melhores ajustados que encontramos para essa situação foram:


Evolução temporal da Energia Total:
<math>C = 0,05; S= 0,3; M = 0,15; B = 0,6</math>


[[Arquivo:time_evolution_U_d_03.png|500px|center]]
[[Arquivo:Predador.jpg |thumb|none|500px| BOIDs na presença de dois predadores.]]


Observa-se que o sistema se encontra em equilíbrio a <math>10^5</math> passos  Monte Carlo. Isso é corroborado pelos resultados do artigo de M Rovere et al. A partir do sistema equilibrado, são analisadas a distribuição de densidade e a função distribuição de pares para verificar a presença de uma (líquida) ou duas fases (líquida, gasosa), usando uma média de <math>10^5</math> medidas sucessivas.
[[Arquivo:PREDADOR.gif |thumb|none|500px| Animação dos BOIDs na presença de dois predadores. Código[https://fiscomp.if.ufrgs.br/index.php/Grupo_-_BOIDS/codigo_BOIDS_predador]]]


Para <math> T = 0.70</math> temos  que:
= Conclusão =
O comportamento coletivo sincronizado de animais é muito complexo. O estudo do cardume de peixes num sistema 2D é uma simplificação mas que nos dá ideias boas das regras básicas de comportamento e otimizações posteriores sobre o objeto de estudo. A regra modificada de alinhamento nos trás um comportamento mais real do cardume de peixes. Outras otimizações poderiam inserir diversas outras regras, como por exemplo um sentimento de nervosismo no bando pela presença de muitos predadores pode fazer o grupo se mover mais rápido e etc. Além disso o algoritmo BOID se torna muito intuitivo de ser trabalhado, podendo ser tratado com regras distintas, ligando e desligando como quisermos.


[[Arquivo: snapshot_t70_d_03.png|300px]] [[Arquivo: P_t70_d_03.png|300px]] [[Arquivo: g_t70_d_03.png|300px]]
=Desenvolvimento em C=
Abaixo verá trechos do código em linguagem de programação C utilizados no trabalho para as regras e etapas.


Nesse caso observa-se apenas uma fase, com a densidade média sendo a densidade global do sistema, que é diferente do centro do pico (<math> \rho \approx 1.0 </math>). Isso caracteriza a fase gasosa, que ocupa todo o espaço disponível. A função distribuição de pares rapidamente converge para 1 com pequenas oscilações, caracterizando um gás de alta densidade.
Link para o código completo[https://fiscomp.if.ufrgs.br/index.php/Grupo_-_BOIDS/codigo].


Para <math> T = 0.50</math> temos  que:
== Coesão ==
<br />


[[Arquivo: snapshot_t50_d_03.png|300px]] [[Arquivo: P_t50_d_03.png|300px]] [[Arquivo: g_t50_d_03.png|300px]]
<source lang="c">


Nesse caso observa-se a coexistência das fases gasosa e líquida. Além disso, pode-se observar a densidade característica aproximada de cada fase a essa temperatura centrada nos respectivos picos (<math> \rho_g \approx 0.2 </math> e <math> \rho_l \approx 2.0 </math>). A função distribuição de pares representa a de uma fase líquida.
      //**********Coesao Entre Particulas e CM**********//
     
     
      for(m=0;m<N;m++){ // laço das particulas
if(norm(r[j][1]-r[m][1],r[j][0]-r[m][0])<R){// se as particulas tiverem a uma distancia menor q "R"
  cont++;          // acrescenta no contador
  x = x + r[m][0]; // acrescenta na posicao das particulas na comp. x
  y = y + r[m][1]; // acrescenta na posicao das particulas na comp. y
}
      }
     
      if(cont>1){ // se contador for cont > 1
x = x/cont;    // media aritmetica na componente x     
y = y/cont;    // media aritmetica a componente y
v[j][0] = v[j][0] - C*(r[j][0] - x)/L; // atualiza velocidade c potencial de mola na componente x
v[j][1] = v[j][1] - C*(r[j][1] - y)/L; // atualiza velocidade c potencial de mola na componente y
      } 
     


Para <math> T = 0.45</math> temos  que:
</source><br />


[[Arquivo: snapshot_t45_d_03.png|300px]] [[Arquivo: P_t45_d_03.png|300px]] [[Arquivo: g_t45_d_03.png|300px]]


Nesse gráfico a primeira impressão é de coexistência de fases. Apesar disso, densidade zero não corresponde a uma fase real, e sim aos espaços vazios. Dessa forma, a fase aqui é a líquida. O ''snapshot'' permite visualizar isso, já que há aglomerados de densidade aparentemente constante separados por espaços praticamente sem partículas. A densidade da fase líquida a essa temperatura é aproximadamente o centro do pico da direita (<math> \rho \approx 2.3 </math>).
== Separação ==
<br />


Para <math> T = 0.30</math> temos  que:
<source lang="c">


[[Arquivo: snapshot_t30_d_03.png|300px]] [[Arquivo: P_t30_d_03.png|300px]] [[Arquivo: g_t30_d_03.png|300px]]  
      //**********Separacao Entre Particulas**********//
     
      for(l=0;l<N;l++){ //laço para particulas
if(l==j){  // se a particula for ela mesma nao faz nada
 
}else{    // se nao é ela entao
 
  if(norm(r[j][0]-r[l][0],r[j][1]-r[l][1])<rmin){ // se as particulas estao a uma distancia menor que  "rmin"
    v[j][0] = v[j][0] + S*(r[j][0] - r[l][0])/pow(norm(r[l][0]-r[j][0],r[l][1]-r[j][1]),2); // Atualiza velocidade c potencial analogo a lei de Coulomb na componente x
           
    v[j][1] = v[j][1] + S*(r[j][1] - r[l][1])/pow(norm(r[l][0]-r[j][0],r[l][1]-r[j][1]),2); // Atualiza velocidade c potencial analogo a lei de Coulomb na componente y
           
  }
}
      }
     


Assim como no gráfico anterior, há dois picos mas apenas um representa uma fase. A principal diferença é que o pico em zero é bem maior e mais agudo que no caso <math> T = 0.45</math>, o que ilustra que há mais espaço vazio. A densidade do líquido aqui é <math> \rho \approx 2.8 </math>. Nota-se que o sistema parece estar se organizando numa fase hexagonal, apesar de ainda ser amorfa, e a densidade já é bem mais alta. A distribuição de pares tem mínimos bem menores do que para os parâmetros acima tratados, caracterizando um sistema que parece estar próximo da transição para a fase hexagonal de baixa energia.


De maneira geral, é possível estimar o intervalo de parâmetros para o qual ocorre a transição de fase líquido-gás. É possível, também, visualizar, a partir da distribuição de densidades, a coexistência de fases, já que cada estado tem uma densidade média característica a dada temperatura.
</source><br />


=== Transição de fase com temperatura fixa ===
== Alinhamento (vetor Velocidade) ==
<br />


Dado a temperatura fixa <math> T = 0.45 </math>, é observado o sistema para as diferentes densidades <math> \rho \in \{0.10, 0.30, 0.40\}</math>.
<source lang="c">


Evolução temporal da Energia Total:
    //**********Media da Velocidade dos Vizinhos**********//
     
     
      for(k=0;k<N;k++){ // laço para todas as particulas
if(k == j){  // se eh a mesma particula nao faz nada
}else if(norm(r[j][1]-r[k][1],r[j][0]-r[k][0])<erre){
  kont++;              // se eh outra particula acrescenta no contador
  vmx = vmx + v[k][0]; // acrescenta a velocidade na componente x
  vmy = vmy + v[k][1]; // acrescenta a velocidade na componente y
}
      }
     
      if(kont > 1){
v[j][0] = (1-M)*v[j][0] + M*(vmx/kont); // media com peso M para a vel.
v[j][1] = (1-M)*v[j][1] + M*(vmy/kont); // dos vizinhos e a propria
      }
       
     


</source><br />


[[Arquivo:time_evolution_U_T_45.png|500px|center]]
== Ruído ==


<br />


Observa-se que o sistema se encontra em equilíbrio a <math>10^5</math> passos  Monte Carlo. Isso é corroborado pelos resultados do artigo de M Rovere et al. A partir do sistema equilibrado, são analisadas a distribuição de densidade e a função distribuição de pares para verificar a presença de uma (líquida) ou duas fases (líquida, gasosa), usando uma média de <math>10^5</math> medidas sucessivas.
<source lang="c">


Para <math> \rho = 0.10</math> temos que:
      //**********Ruido**********//
      if(rand()%2 == 0){ // criterio para decidir a fase
randomi = - rand()/RAND_MAX; // fase
      }else{
randomi = rand()/RAND_MAX; // fase
      }
      v[j][0] = cos(randomi)*v[j][0] + sin(randomi)*v[j][1]; // rotaçao
      v[j][1] = - sin(randomi)*v[j][0] + cos(randomi)*v[j][1]; // rotaçao


[[Arquivo: snapshot_t45_d_10.png|300px]] [[Arquivo: P_t45_d_10.png|300px]] [[Arquivo: g_t45_d_10.png|300px]]
</source><br />


Observa-se no ''snapshot'' que o sistema parece ter fase líquida e fase gasosa coexistindo. O resultado da distribuição de densidades pode ter sido afetado pelo aumento da área (consequentemente  também das células usadas para realização do histograma) já que o sistema ficou maior a fim de diminuir a densidade mantendo o número de partículas. Apesar disso, o resultado da função distribuição de pares parece razoável com a hipótese da fase líquida estar presente.
== Predador ==


Para <math> \rho = 0.30</math> temos  que:
<br />


[[Arquivo: snapshot_t45_d_03.png|300px]] [[Arquivo: P_t45_d_03.png|300px]] [[Arquivo: g_t45_d_03.png|300px]]
<source lang="c">


Esse gráfico foi tratado anteriormente (para temperatura fixa) e está reproduzido novamente a fim de comparação.
      //Barreira puntual no centro
      if(norm(r[j][0] -bx, r[j][1] - by) < ERRE){ // se a particula ta a menos
                                          //  de "ERRE" entao
if(r[j][0] < bx && r[j][1] < by){ // se estiver atras e abaixo
  v[j][0] = v[j][0] - B*norm(r[j][0] - bx, r[j][0] - bx)/pow(norm(r[j][0] - bx, r[j][1]- by),1.5); // atualiza velocidade com potencial analogo "gravitac"
  v[j][1] = v[j][1] - B*norm(r[j][1] - by, r[j][1] - by)/pow(norm(r[j][0] - bx, r[j][1]- by),1.5); // atualiza velocidade com potencial analogo "gravitac"
 
}else if(r[j][0] > bx && r[j][1] < by){ // se estiver a frente e abaixo
  v[j][0] = v[j][0] + B*norm(r[j][0] - bx, r[j][0] - bx)/pow(norm(r[j][0] - bx, r[j][1]- by),1.5); // atualiza velocidade com potencial analogo "gravitac"
  v[j][1] = v[j][1] - B*norm(r[j][1] - by, r[j][1] - by)/pow(norm(r[j][0] - bx, r[j][1]- by),1.5); // atualiza velocidade com potencial analogo "gravitac"
 
}else if(r[j][0] < bx && r[j][1] > by){ // se estiver abaixo e acima
  v[j][0] = v[j][0] - B*norm(r[j][0] - bx, r[j][0] - bx)/pow(norm(r[j][0] - bx, r[j][1]- by),1.5);// atualiza velocidade com potencial analogo "gravitac"
  v[j][1] = v[j][1] + B*norm(r[j][1] - by, r[j][1] - by)/pow(norm(r[j][0] - bx, r[j][1]- by),1.5);// atualiza velocidade com potencial analogo "gravitac"
 
}else if(r[j][0] > bx && r[j][1] > by){// se estiver a frente e acima
  v[j][0] = v[j][0] + B*norm(r[j][0] - bx, r[j][0] - bx)/pow(norm(r[j][0] - bx, r[j][1]- by),1.5); // atualiza velocidade com potencial analogo "gravitac"
  v[j][1] = v[j][1] + B*norm(r[j][1] - by, r[j][1] - by)/pow(norm(r[j][0] - bx, r[j][1]- by),1.5); // atualiza velocidade com potencial analogo "gravitac"
}


Para <math> \rho = 0.40</math> temos  que:
      }


[[Arquivo: snapshot_t45_d_40.png|300px]] [[Arquivo: P_t45_d_40.png|300px]] [[Arquivo: g_t45_d_40.png|300px]]
</source><br />


Nesse sistema há a presença de fase líquida com menos espaços vazios. O pico de densidade da fase líquida situa-se em <math> \rho \approx 1.5 </math>. Essa queda da densidade do líquido com aumento da densidade do sistema indica que uma transição de fase para gás pode estar próxima para esses parâmetros.
=Referências=
 
*https://en.wikipedia.org/wiki/Boids
Para <math> \rho = 0.70</math> temos  que:
*Reynolds, C. W. (1987) Flocks, Herds, and Schools: A Distributed Behavioral Model, in Computer Graphics, 21(4) (SIGGRAPH '87 Conference Proceedings) pages 25-34.
 
*Vicsek, T.; Czirok, A.; Ben-Jacob, E.;; Cohen, I.; Shochet, O. (1995). "Novel type of phase transition in a system of self-driven particles". Physical Review Letters. 75: 1226–1229. [https://arxiv.org/abs/cond-mat/0611743 arXiv:cond-mat/0611743]
[[Arquivo: snapshot_t45_d_70.png|300px]] [[Arquivo: P_t45_d_70.png|300px]] [[Arquivo: g_t45_d_70.png|300px]]
 
Observa-se que o sistema tem relativa homogeneidade e ocupa toda a área. Isso se caracteriza como um gás, como pode ser verificado na distribuição de densidade, que tem apenas um pico em  <math> \rho \approx 1.0 </math> (que não é a média global). Apesar disso, o sistema parece relativamente organizado, o que sugere uma possível transição de fase. Também sugere isso a distribuição de pares, que tem mínimos baixos que remetem à fase sólida.
 
== Sistema tridimensional ==
 
Dado um sistema tridimensional com densidade <math> \rho = N / L^3</math> e temperatura <math>T</math>, os diagramas foram feitos com:
 
(A) <math> N = 500 </math> partículas
(B) Cubo de lado <math> L =  (N / \rho)^{1/3} </math> com convenção da imagem mínima
(C) Incialização aleatória
(D) Distância de corte <math>r_c \in \{2.5 \sigma, 3.0 \sigma, 3.5 \sigma \} </math>
(E) Deslocamento máximo inicial <math>\Delta_0 = L/2 </math>
 
=== Transição de fase líquido-gás ===
Conforme o trabalho desenvolvido por Nicholas et al <ref>J.J. Nicolas, K.E. Gubbins, W.B. Streett, and D.J. Tildesley (1979). "Equation of state for
the Lennard-Jones fluid". Mol. Phys., 37</ref>, os valores críticos na transição de fase líquido-gás para um fluido de Lennard-Jones tridimensional são <math>T_{cr} =  1.35</math> e <math>\rho_{cr} = 0.35</math>.
 
=== T = 2.0 (acima do valor crítico)===
 
Tendo em vista que a análise no equilíbrio do sistema bidimensional foi feita após <math> 10^5 </math> passos Monte Carlo, é bastante possível que os sistemas tridimensionais aqui tratados não tenham alcançado o equilíbrio. Para  <math>r_c  = 2.5\sigma</math>, temos a evolução temporal da energia total e da pressão:
 
[[Arquivo: t_t20_r25_U.png|500px]] [[Arquivo: t_t20_r25_P.png|500px]]
 
Estimando seus valores a partir do equilíbrio, determina-se o diagrama de fase:
 
[[Arquivo:t20_r25_Pd.png|500px|center]]
 
Além disso, tem-se as diferentes configurações espaciais para as densidades <math>\rho = 0.2</math> e <math>\rho = 0.6</math>, respectivamente:
 
[[Arquivo:g_t20_d02_r25.png|500px]] [[Arquivo:g_t20_d06_r25.png|500px]]
 
Executando o mesmo esquema, o diagrama é comparado para diferentes valores de  <math>r_c</math>:
 
[[Arquivo:t20_Pd.png|500px|center]]
 
Nessa situação (acima do valor crítico de temperatura), o gráfico pressão - densidade mostra sua injetividade, e portanto, a não coexistência de fases (como esperado).
 
==Referências==
<references />

Edição atual tal como às 10h51min de 19 de janeiro de 2020

Alunos: Álvaro Essinger, Pedro Widniczck.

Contexto Histórico

Desenvolvido por Craig Reynolds, engenheiro de software, em 1986, é um algoritmo que busca, por meio de regras básicas, reproduzir o comportamento sincronizado de grupos de animais. Por exemplo manadas de animais terrestres, cardumes de peixes, bando de pássaros e etc. O nome BOID corresponde ao encurtamento da expressão em inglês “bird-oid object”, que se refere a um objeto “tipo pássaro”. Seu trabalho foi publicado em 87 sob o título original, em inglês, "Flocks, herds and schools: A distributed behavioral model". O modelo base de Craig já fora utilizado para diversas implementações e estudos. Como estudo comportamental de medo, interação entre animais via olfato modelando feromônios, mudança de liderança de um bando, dentre muitas outras aplicações interessantes.

Posteriormente, em 1995, Tamás Vicsek, cientista húngaro, apresentou um modelo simplificado de BOID para o estudo de transições de fase de um sistema desordenado para um estado ordenado de larga escala. Esse tipo de transição espontânea é um exemplo de movimento coletivo. Esse modelo é bastante popular atualmente na área da física.

Motivação

O movimento de animais em sincronia é extremamente complexo e é chave para sua sobrevivência em bando. Peixes, pássaros e mamíferos terrestres tem esse tipo de comportamento principalmente no que diz respeito a defesa em momentos em que sentem em perigo. A concentração intimida e o movimento confunde seus predadores. Além de ser extremamente prazeroso assistir um bando de pássaros ou um cardume de peixes em sua dança sincronizada.

Este trabalho busca, em suas etapas, reproduzir um cardume de peixes em seu padrão síncrono de movimento e, posteriormente, na presença de um ou mais predadores.


O Algoritmo Para BOIDS

Inicialmente são sorteadas posições e velocidades aleatórias para os objetos. As regras são então calculadas a cada de passo temporal. Embora cada boid tenha liberdade sobre todo o espaço descrito, o seu comportamento é influenciado apenas por outros dentro de uma região circular centrada no objeto dita raio de interação (R). Após o cálculo das novas posições e velocidades é somado um incremento de tempo e o algoritmo recomeça.

Separação

Interação de repulsão entre os indivíduos para evitar superconcentração local (ou no caso extremo uma superposição). Uma força central, dependente apenas da distância entre o boid e a origem da força:

, onde e é o coeficiente de separação.

Fig1. link:https://en.wikipedia.org/wiki/Boids#/media/File:Rule_separation.gif

Alinhamento (vetor velocidade)

A velocidade média dos parceiros próximos influencia o vetor velocidade do objeto, fazendo-o ter um comportamento parecido com sua vizinhança.

, com sendo o número de vizinhos dentro do raio de interação.

Fig2. link:https://en.wikipedia.org/wiki/Boids#/media/File:Rule_alignment.gif

Coesão

Os BOIDs interagentes tem um potencial de mola entre si, fazendo com que tenham a tendência de mover-se em direção ao centro de massa do grupo. Calculando primeiramente o centro de massa (CM) das partículas vizinhas utiliza-se da força elástica para simular uma mola entre o objeto e o CM da vizinhança.

, com sendo o número de partículas dentro do raio de interação.

, e sendo o coeficiente elástico.


Fig3. link:https://en.wikipedia.org/wiki/Boids#/media/File:Rule_cohesion.gif

Ruído

Para reproduzir melhor um ser vivo, um pequeno ruído compõe a velocidade. Isso faz com que tenhamos uma maior flutuação no caminho que os boids traçam.

sendo um número real aleatório,

, na componente x

e

, na componente y.

BOIDS Adaptados Para Cardume de Peixes

Para a realização da adaptação, utiliza-se outra regra de alinhamento, fazendo uma média ponderada entre a velocidade do boid no tempo t com a velocidade dos vizinhos, da forma:

, M sendo o termo da média.

as outras relaçoes, separação e coesão continuam idênticas. Porém também serão acrescentadas uma barreira repulsiva que dificulte a chegada dos boids na fronteira, sendo a constante de proporcionalidade e E o raio de interação da barreira, da seguinte forma:

, para quando o boid se aproxima da extremidade superior do dominio, idem para componente x,

, para quando o boid se aproxima da parte inferior do dominio. Idem para componente x,

para todos os programas se L = 100, então E = 10 e para L = 1000 então E = 50.

Também é feito que, para todos os boids que possuem mais de vizinhos, sejam freiados, pois foi observado que peixes quando na presença de vizinhos (semelhantes) diminuem suas velocidades.

Predador

A partícula que representa o predador é uma barreira repulsiva. Obedecendo a

, onde B é o coeficiente da barreira e b é a posição do k-ésimo predador.

No presente trabalho o predador não persegue os BOIDs, apenas se desloca em linha reta no plano com velocidade constante.

Aqui[5] é possível ver o comportamento de um cardume de peixes na presença de algumas arraias.

Resultados e Discussão

Nosso modelo foi simulado com condições de contorno periódicas em áreas quadradas de lados e . Abaixo apresentamos os resultados para cada regra isoladamente e ao final todas funcionando simultaneamente com e sem a presença do predador.

Separação

Aqui temos, como esperado, um comportamento semelhante ao de um gás ideal. Que busca um estado de menor energia ocupando todo o espaço disponível. Note que poucas regiões tem mais de 3 objetos próximos.

Simulação apenas da regra de separação entre BOIDS.

A animação abaixo busca ilustrar a dependência do parâmetro no sistema, aumentando-o progressivamente.

Simulação apenas da regra de separação entre BOIDS.

Coesão

Para a coesão temos um comportamento semelhante ao condensamento de um gás em gotas ou gotículas. As regiões mais concentradas (círculo verde) perdem um pouco de sua capacidade de mobilidade e se tornam atrativas para partículas vizinhas (círculos azuis). Ao passo que objetos isolados (círculos roxos) se comportam independentemente até encontrarem um, ou mais, vizinhos ou regiões de alta concentração.

Simulação apenas da regra de coesão entre BOIDS.

Na animação abaixo temos o comportamento dinâmico do sistema para o parâmetro crescente. Note que, de fato, a medida que aumenta, também ocorre o aumento da concentração dos BOIDs.

Simulação apenas da regra de coesão entre BOIDS.

Alinhamento (vetor velocidade)

Na regra de alinhamento temos o comportamento do vetor velocidade do objeto sendo influenciado pela velocidade das partículas na vizinhança. Na imagem estática fica difícil de diferenciar da regra de separação, porém, note como aqui há mais regiões com 3 ou mais BOIDs bem próximos. Em alguns casos pode-se notar que quase ocorre uma superposição.

Simulação apenas da regra de alinhamento entre BOIDS.

A animação abaixo ilustra a influência da regra mostrando o sistema inicialmente com o alinhamento desligado e ligando-o logo após.

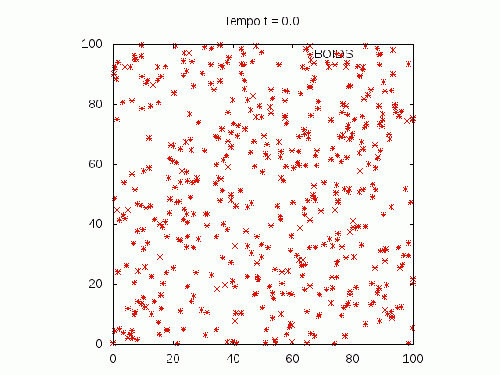
Animação da regra de alinhamento entre BOIDS.

BOIDS (3 regras ligadas)

Aqui temos a implementação das 3 regras básicas ligadas.

Os parâmetros usados nessa simulação foram: , nesse caso não temos o parâmetro pois só é utilizada a media aritmética das componentes.

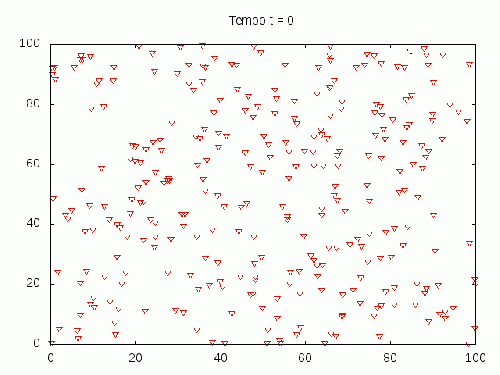
Animação BOIDS sem adaptação de cardume. Código:[1]

BOIDS Adaptados Para Cardume de Peixes

Implementação das 2 regras básicas de coesão e separação com a modificação da regra de alinhamento buscando um comportamento de grupo mais real. Note que aqui, ao se juntarem, a velocidade diminui. Pois a velocidade está dependo da quantidade de vizinhos.

Os parâmetros utilizados foram:


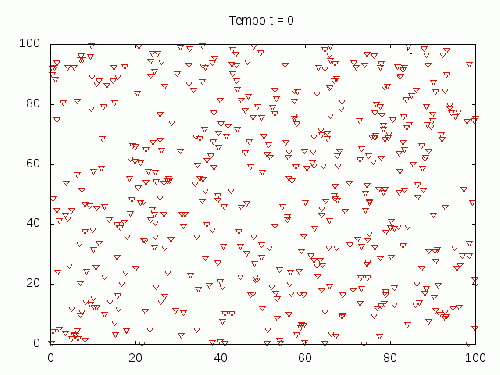
Simulação BOIDS com otimização de velocidade do cardume. Código: [2]

Para melhorar o comportamento do cardume, fora implementada uma barreira fraca nas bordas da região. Isso fará muita diferença na visualização da situação com predadores.

Na situação abaixo foram usados os seguintes parâmetros:

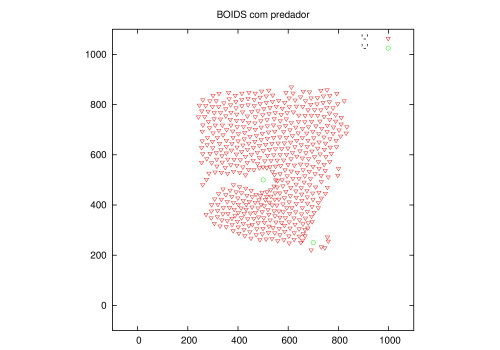
Simulação BOIDS com otimização de velocidade do cardume e barreira fraca nas bordas. Código[3]

Predador

Resultado obtido com as regras de coesão, separação e alinhamento adaptado para cardume de peixes implementadas. Aqui buscamos colocar os predadores em cena depois de algum tempo dos objetos criados para que o cardume se organize.

Os parâmetros melhores ajustados que encontramos para essa situação foram:

BOIDs na presença de dois predadores.
Animação dos BOIDs na presença de dois predadores. Código[4]

Conclusão

O comportamento coletivo sincronizado de animais é muito complexo. O estudo do cardume de peixes num sistema 2D é uma simplificação mas que nos dá ideias boas das regras básicas de comportamento e otimizações posteriores sobre o objeto de estudo. A regra modificada de alinhamento nos trás um comportamento mais real do cardume de peixes. Outras otimizações poderiam inserir diversas outras regras, como por exemplo um sentimento de nervosismo no bando pela presença de muitos predadores pode fazer o grupo se mover mais rápido e etc. Além disso o algoritmo BOID se torna muito intuitivo de ser trabalhado, podendo ser tratado com regras distintas, ligando e desligando como quisermos.

Desenvolvimento em C

Abaixo verá trechos do código em linguagem de programação C utilizados no trabalho para as regras e etapas.

Link para o código completo[6].

Coesão


      //**********Coesao Entre Particulas e CM**********//
      
      
      for(m=0;m<N;m++){ // laço das particulas 
	if(norm(r[j][1]-r[m][1],r[j][0]-r[m][0])<R){// se as particulas tiverem a uma distancia menor q "R"
	  cont++;          // acrescenta no contador 
	  x = x + r[m][0]; // acrescenta na posicao das particulas na comp. x
	  y = y + r[m][1]; // acrescenta na posicao das particulas na comp. y
	}	 
      }
      
      if(cont>1){ // se contador for cont > 1
	x = x/cont;     // media aritmetica na componente x       
	y = y/cont;     // media aritmetica a componente y
	
	v[j][0] = v[j][0] - C*(r[j][0] - x)/L; // atualiza velocidade c potencial de mola na componente x
	v[j][1] = v[j][1] - C*(r[j][1] - y)/L; // atualiza velocidade c potencial de mola na componente y 
      }



Separação


      //**********Separacao Entre Particulas**********//
      
      for(l=0;l<N;l++){ //laço para particulas
	if(l==j){  // se a particula for ela mesma nao faz nada 
	  
	}else{     // se nao é ela entao
	  
	  if(norm(r[j][0]-r[l][0],r[j][1]-r[l][1])<rmin){ // se as particulas estao a uma distancia menor que  "rmin"
	    v[j][0] = v[j][0] + S*(r[j][0] - r[l][0])/pow(norm(r[l][0]-r[j][0],r[l][1]-r[j][1]),2); // Atualiza velocidade c potencial analogo a lei de Coulomb na componente x
	            
	    v[j][1] = v[j][1] + S*(r[j][1] - r[l][1])/pow(norm(r[l][0]-r[j][0],r[l][1]-r[j][1]),2); // Atualiza velocidade c potencial analogo a lei de Coulomb na componente y
	            
	  }
	}
      }


Alinhamento (vetor Velocidade)


    //**********Media da Velocidade dos Vizinhos**********//
      
      
      for(k=0;k<N;k++){ // laço para todas as particulas
	if(k == j){  // se eh a mesma particula nao faz nada
	}else if(norm(r[j][1]-r[k][1],r[j][0]-r[k][0])<erre){ 
	  kont++;              // se eh outra particula acrescenta no contador
	  vmx = vmx + v[k][0]; // acrescenta a velocidade na componente x
	  vmy = vmy + v[k][1]; // acrescenta a velocidade na componente y
	}
      }
      
      if(kont > 1){
	v[j][0] = (1-M)*v[j][0] + M*(vmx/kont); // media com peso M para a vel.
	v[j][1] = (1-M)*v[j][1] + M*(vmy/kont); // dos vizinhos e a propria
      }


Ruído


      //**********Ruido**********//
      if(rand()%2 == 0){ // criterio para decidir a fase
	randomi = - rand()/RAND_MAX; // fase
      }else{
	randomi = rand()/RAND_MAX; // fase
      }
      v[j][0] = cos(randomi)*v[j][0] + sin(randomi)*v[j][1];  // rotaçao
      v[j][1] = - sin(randomi)*v[j][0] + cos(randomi)*v[j][1]; // rotaçao


Predador


      //Barreira puntual no centro
      if(norm(r[j][0] -bx, r[j][1] - by) < ERRE){ // se a particula ta a menos
	                                          //  de "ERRE" entao
	
	if(r[j][0] < bx && r[j][1] < by){ // se estiver atras e abaixo
	  v[j][0] = v[j][0] - B*norm(r[j][0] - bx, r[j][0] - bx)/pow(norm(r[j][0] - bx, r[j][1]- by),1.5); // atualiza velocidade com potencial analogo "gravitac"
	  v[j][1] = v[j][1] - B*norm(r[j][1] - by, r[j][1] - by)/pow(norm(r[j][0] - bx, r[j][1]- by),1.5); // atualiza velocidade com potencial analogo "gravitac"
	  
	}else if(r[j][0] > bx && r[j][1] < by){ // se estiver a frente e abaixo
	  v[j][0] = v[j][0] + B*norm(r[j][0] - bx, r[j][0] - bx)/pow(norm(r[j][0] - bx, r[j][1]- by),1.5); // atualiza velocidade com potencial analogo "gravitac"
	  v[j][1] = v[j][1] - B*norm(r[j][1] - by, r[j][1] - by)/pow(norm(r[j][0] - bx, r[j][1]- by),1.5); // atualiza velocidade com potencial analogo "gravitac"
	  
	}else if(r[j][0] < bx && r[j][1] > by){ // se estiver abaixo e acima
	  v[j][0] = v[j][0] - B*norm(r[j][0] - bx, r[j][0] - bx)/pow(norm(r[j][0] - bx, r[j][1]- by),1.5);// atualiza velocidade com potencial analogo "gravitac"
	  v[j][1] = v[j][1] + B*norm(r[j][1] - by, r[j][1] - by)/pow(norm(r[j][0] - bx, r[j][1]- by),1.5);// atualiza velocidade com potencial analogo "gravitac"
	  
	}else if(r[j][0] > bx && r[j][1] > by){// se estiver a frente e acima
	  v[j][0] = v[j][0] + B*norm(r[j][0] - bx, r[j][0] - bx)/pow(norm(r[j][0] - bx, r[j][1]- by),1.5); // atualiza velocidade com potencial analogo "gravitac"
	  v[j][1] = v[j][1] + B*norm(r[j][1] - by, r[j][1] - by)/pow(norm(r[j][0] - bx, r[j][1]- by),1.5); // atualiza velocidade com potencial analogo "gravitac"
	}

      }


Referências

  • https://en.wikipedia.org/wiki/Boids
  • Reynolds, C. W. (1987) Flocks, Herds, and Schools: A Distributed Behavioral Model, in Computer Graphics, 21(4) (SIGGRAPH '87 Conference Proceedings) pages 25-34.
  • Vicsek, T.; Czirok, A.; Ben-Jacob, E.;; Cohen, I.; Shochet, O. (1995). "Novel type of phase transition in a system of self-driven particles". Physical Review Letters. 75: 1226–1229. arXiv:cond-mat/0611743
Disponível em “http://fiscomp.if.ufrgs.br/index.php?title=BOIDS&oldid=2741”