Ressonância Estocástica: mudanças entre as edições
| (87 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 2: | Linha 2: | ||
== Introdução == | == Introdução == | ||
A ressonância estocástica é o fenômeno em sistemas não-lineares em que sinais fracos podem ser amplificados e otimizados por um ruído branco, sendo o efeito encontrado em função do nível de ruído e de características do sistema e do sinal. | A ressonância estocástica (RE) é o fenômeno em sistemas não-lineares em que sinais fracos podem ser amplificados e otimizados por um ruído branco, sendo o efeito encontrado em função do nível de ruído e de características do sistema e do sinal. <ref name=stc_res> Reviews of Modern Physics, Vol. 70, No. 1, January 1998 - Stochastic resonance - Luca Gammaitoni, Sezione di Perugia, Peter Hänggi, Peter Jung, and Fabio Marchesoni</ref> | ||
=== Linear vs não linear | === Linear vs não linear === | ||
A concepção convencional é de que ruídos deterioram um sinal, oposto do que acontece na Ressonância Estocástica (RE). Um ponto chave para essa discrepância é a distinção entre sistemas lineares e não-lineares. | A concepção convencional é de que ruídos deterioram um sinal, oposto do que acontece na Ressonância Estocástica (RE). Um ponto chave para essa discrepância é a distinção entre sistemas lineares e não-lineares. | ||
Em termos gerais, em sistemas lineares, a combinação de duas entradas resulta em uma saída equivalente à combinação das saídas que o sistema daria para cada entrada | |||
Sistemas não-lineares, por outro lado, são todos aqueles que não são lineares. | Em termos gerais, em sistemas lineares, a combinação de duas entradas resulta em uma saída equivalente à combinação das saídas que o sistema daria para cada entrada separada. <ref name=lin_mod> MIT News, February 26, 2010 - “Explained: Linear and Nonlinear Systems” - Larry Hardesty - https://news.mit.edu/2010/explained-linear-0226</ref> Ou seja, para uma função <math>f</math> linear, se <math>f(x) = y</math> e <math>f(a) = b</math>, então <math>f(x+a) = y+b</math>. | ||
É de se esperar que em sistemas lineares a adição de ruído possa apenas degradar ou mascarar um sinal inicial (o exemplo mais simples é a soma direta do ruído ao sinal). A RE é portanto um processo próprio de sistemas não-lineares. A não-linearidade, contudo, não é condição suficiente para que o fenômeno ocorra. | |||
Sistemas não-lineares, por outro lado, são todos aqueles que não são lineares. <ref name=lin_mod/> | |||
É de se esperar que em sistemas lineares a adição de ruído possa apenas degradar ou mascarar um sinal inicial (o exemplo mais simples é a soma direta do ruído ao sinal). A RE é, portanto, um processo próprio de sistemas não-lineares. A não-linearidade, contudo, não é condição suficiente para que o fenômeno ocorra. | |||
'''Condições para RE:''' | '''Condições para RE:''' | ||
Em geral, são condições necessárias para RE [1]: | Em geral, são condições necessárias para RE: <ref name=stc_res/> | ||
- ''Barreira/limiar'': um “obstáculo” à percepção de um sinal ou ao acontecimento de um evento. Um exemplo simples seria o efeito de “delta” em: | |||
<math>f(x) = x</math>, se <math>x > \delta</math>; <math>f(x) = 0</math>, se <math>x <= \delta</math> | |||
- ''Sinal fraco coerente'': um sinal (entrada) que obedeça certo padrão e não seja, em geral, capaz de “superar” a barreira ou limiar associado ao sistema. O sentido físico dessa “superação” depende do sistema. Seguindo o exemplo anterior, essa condição seria satisfeita se <math>x <= \delta</math> fosse verdade para todo <math>x</math>, por exemplo. | |||
- ''Fonte de ruído não correlacionado (ou “ruído branco”)'': um sinal estocástico não-autocorrelacionado, de média zero, que não carrega informação senão por sua intensidade, que é a mesma para todas as frequências (no caso de um ruído branco gaussiano, está ligada ao desvio padrão). | |||
== Breve apanhado histórico == | |||
'''- Primeiras verificações eperimentais:''' | |||
Em tradução livre de <ref name=stc_res/>: | |||
”Uma primeira verificação experimental do fenômeno de ressonância estocástica foi obtida por Fauve e Heslot (1983), que estudaram como a linha espectral de um gatilho de Schmitt dependia do ruído. O campo permaneceu então meio adormecido até a era moderna da ressonância estocástica até ser introduzida por um experimento chave em um ring laser biestável (McNamara, Wiesenfeld, e Roy, 1988).” | |||
'''- Proposta Inicial:''' | |||
A primeira proposta para o fenômeno da RE foi elaborada pouco antes, a partir de 1981, no contexto do estudo sobre eras do gelo [Benzi et al., 1981, 1982, 1983] <ref name=stc_res/>. | |||
Foi observado que as eras glaciais aconteciam com um período da ordem de <math>10^5</math> anos, sendo a variação da excentricidade orbital da Terra o único fenômeno cosmológico relevante com período em ordem comparável. Essas variações, contudo, representam uma diferença de no máximo 0,1% no fluxo de entrada de energia solar na superfície da Terra, o que a princípio não seria suficiente para explicar o fenômeno das eras glaciais. | |||
A solução proposta modelava o sistema como tendo dois locos de estabilidade para temperaturas da Terra (essencialmente os estados “em era do gelo” ou “não em era do gelo”, com uma “barreira” entre eles), uma pequena variação periódica da insolação devido à excentricidade (“sinal”) e variações “aleatórias” anuais de temperatura (“ruído”). A existência das eras do gelo, com sua periodicidade, seria então explicada pelo fenômeno de RE. <ref name=stc_res/> Sistemas assim são chamados biestáveis. | |||
Essa proposta de modelagem acabou por se mostrar limitada <ref name=eras1> P.D. Ditlevsen, Chem. Phys. (2010), doi:10.1016/j.chemphys.2010.05.022 - Extension of stochastic resonance in the dynamics of ice ages - Peter D. Ditlevsen</ref><ref name=eras2> Stochastic Resonance in Glacial Climate - Stefan Rahmstorf and Richard Alley - Revised Version, 17 December 2001</ref>, mas o fenômeno, além das confirmações experimentais já citadas, foi aplicado com sucesso numa grande diversidade de áreas, inclusive no estudo das eras glaciais. | |||
'''- Outros tipos de RE:''' | |||
Após a proposta do primeiro modelo, classificado como biestável por ter dois locos de estabilidade, mais dois tipos importantes de processos de RE começaram a ser estudados: os detectores de limiar e os excitáveis. | |||
Os excitáveis estão relacionados a sistemas com um único estado estável, mas que contam também com um estado excitado de decaimento lento (se comparado à taxa de relaxamento de pequenas perturbações em torno do estado estável). | |||
O exemplo dado na introdução, adicionado de um filtro 1 ou 0, pode ser usado para visualizar a RE de limiar. Em particular, de forma direta, pode ser usado para exemplificar o efeito da RE na percepção humana de sinais visuais com certas características, como veremos em detalhes a seguir. Sistemas excitáveis e de detecção de limiar acabaram por encontrar aplicação em outros campos, como na neurofisiologia de lagostins. <ref name=stc_res/> | |||
== Ressonância estocástica em detectores de limiar == | |||
=== Primeiras noções === | |||
Tomemos inicialmente um sinal com uma intensidade <math>S</math> dada em função de uma posição <math>x</math>, ou seja, <math>S = f(x)</math>, sujeito, para todo <math>x</math>, a um limiar de detecção <math>\delta</math>. A saída do nosso sistema será, para cada <math>x</math>, 1 ou 0 (representados por “branco” ou “preto”) , correspondendo apenas à informação de se o sinal cruzou ou não o limiar - a diferença exata não importa. | |||
Podemos imaginar três casos: | |||
<math>1) F(x) < \delta</math> para todo <math>x</math>, em que o sinal “some”. | |||
<math>2) F(x) > \delta</math> para todo <math>x</math>, em que observa-se que o sinal existe e ultrapassa o limiar em todos pontos, mas não temos ideia de sua estrutura interna para além disso. | |||
<math>3) F(x)</math> com algumas regiões acima de <math>\delta</math> e outras abaixo, onde temos um pouco de informação sobre parte dessa estrutura, mas não de forma geral. | |||
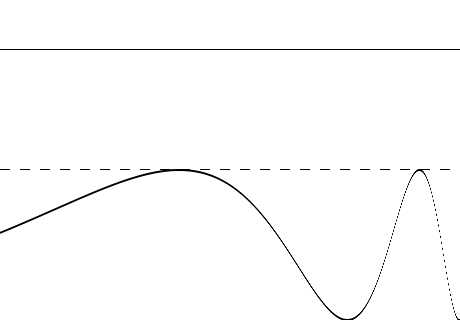
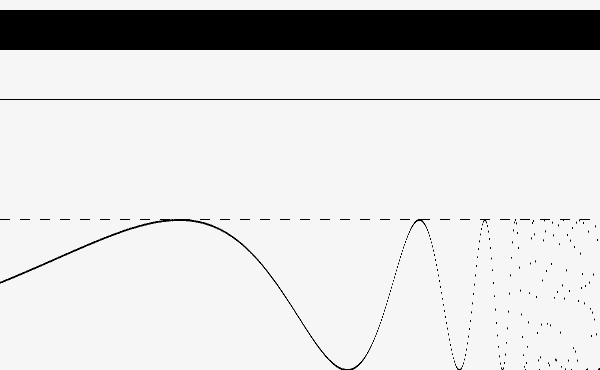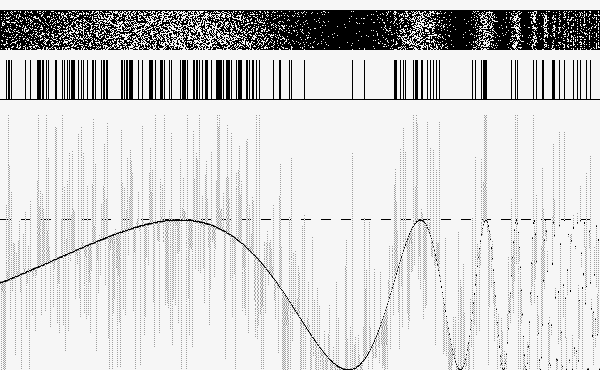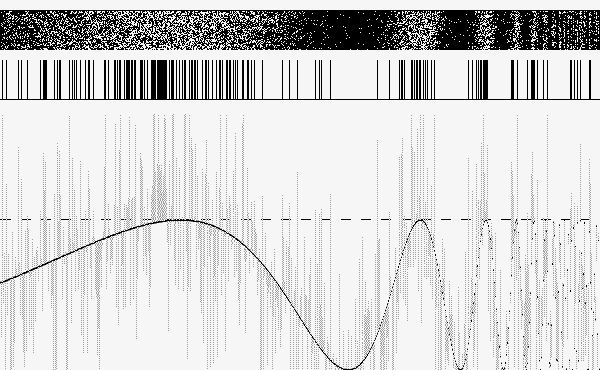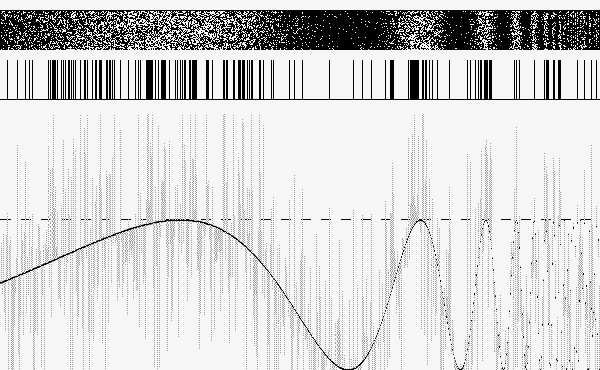
A RE pode ajudar a reconstruir a informação do sinal nos três casos, mas nos exemplos a seguir nos focaremos inicialmente no primeiro, representado na figura 1. | |||
[[Arquivo:Exemplo1_RE.png|frame|400x400px|center|Figura 1: Sinal abaixo do limiar de detecção.]] | |||
O sinal (curva na parte inferior da imagem) não cruza o limiar (linha horizontal tracejada) e, portanto, não há nenhuma ativação. | |||
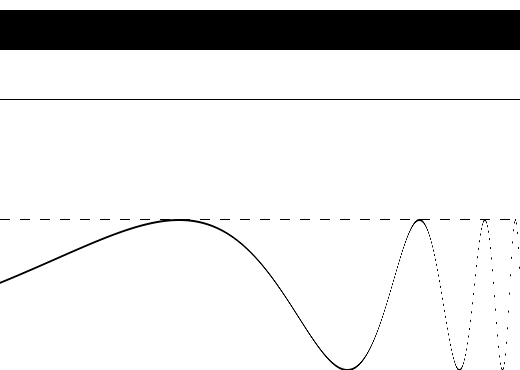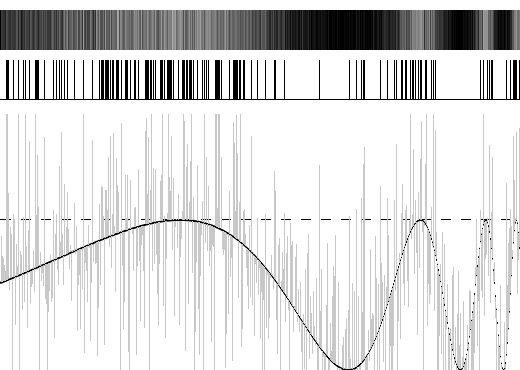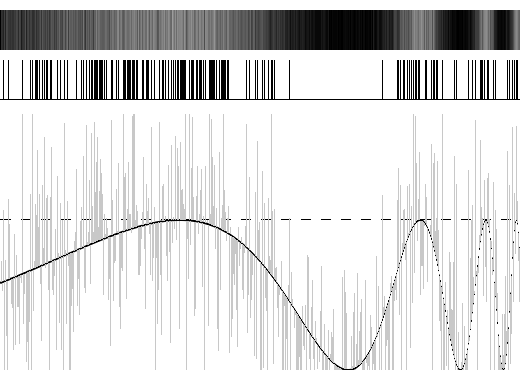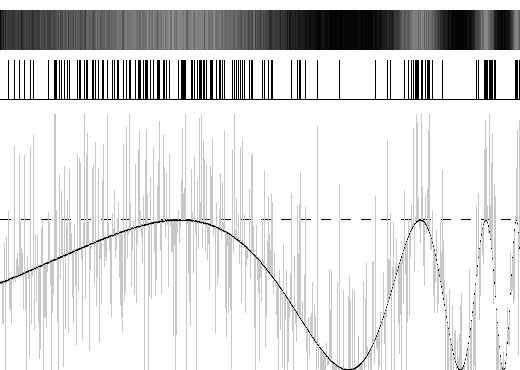
A adição de uma constante ao sinal essencialmente nos leva para o caso 3, ainda não satisfatório, representado na figura 2. | |||
[[Arquivo:Exemplo2_RE.png|frame|400x400px|center|Figura 2: Sinal elevado homogeneamente.]] | |||
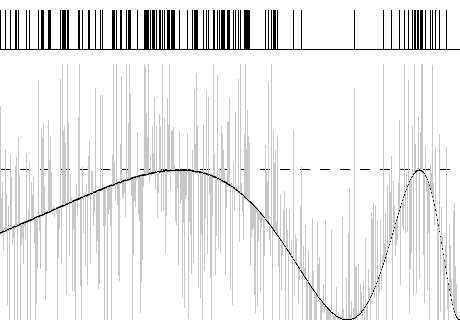
A região cinza representa a “elevação” do sinal, enquanto a região escura localizada na parte superior indica que houve passagem naquelas posições. Finalmente, na figura 3, adicionamos uma realização de “ruído branco” gaussiano, de média zero, ao sinal original: | |||
[[Arquivo:Exemplo3_RE.png|frame|400x400px|center|Figura 3: Sinal com adição de ruído branco gaussiano.]] | |||
Nota-se que a densidade de barras verticais parece ter alguma relação com a forma do sinal original. | |||
=== Percepção visual === | |||
'''- Reconstruindo o sinal original:''' | |||
Realizando o ruído diversas vezes e guardando a informação da quantidade de passagens para cada posição, pode-se estudar a proporção entre o número de passagens e o de realizações. A faixa superior da animação 1 mostra esse comportamento para <math>S = 75(1-\sen(\pi(1-x))</math>, com 100% = branco e 0% = preto: | |||
[[Arquivo:GIF1_RE.gif|frame|400x400px|center|Animação 1: Várias realizações do ruído, com visualização da proporção de detecções.]] | |||
O que acontece é que a natureza da distribuição gaussiana faz com que mesmo pontos muito distantes do limiar possam superá-lo, mas com uma probabilidade menor, a cada realização, em relação à de que outros pontos mais próximos o façam. Como o ruído não guarda autocorrelação, o que acontece com cada ponto em cada realização é independente dos outros, mas a relação entre as probabilidades de cruzamento para cada ponto são constantes e definidas, dependendo apenas do desvio padrão do ruído e da intensidade do sinal em cada ponto. | |||
Ao tomar a média, contudo, o resultado é trazido de volta a um espaço de <math>(256 = 2^8)</math> tons de cinza, em vez do espaço binário preto e branco. Uma alternativa ao cálculo dessa proporção seria simplesmente guardar os diferentes resultados de cada realização, codificados da mesma forma anterior, nas diferentes linhas da faixa superior. A animação 2 mostra o resultado desse processo. | |||
[[Arquivo:GIF2_RE.gif|frame|400x400px|center|Animação 2: Várias realizações do ruído, cada uma usada como uma linha acima.]] | |||
Nota-se que o efeito se mantém: com algumas poucas realizações já é possível, pela percepção visual, estimar detalhes do original. Além da economia de operações, esse sinal reconstruído se mantém binário: representa mais diretamente o que acontece com o sistema e pode, sem compressão, ser codificado em um arquivo de computador usando 1bit por pixel, em vez dos 8 bits por pixel normalmente usados em imagens em tons de cinza (também sem compressão). | |||
Imaginando um sinal 2D, pode-se encontrar uma ligação entre o efeito visto e o processo de dithering <ref name=dither> Physical Review E, vol 61, number 1, jannuary 2000 - Stochastic resonance as dithering - Robert A. Wannamaker, Stanley P. Lipshitz, and John Vanderkooy </ref>, que em uma imagem visa justamente diminuir sua paleta de cores mantendo o máximo da percepção de sua informação original. | |||
'''- O efeito da ressonância estocástica na percepção visual:''' | |||
Em 1997 foi publicado um artigo de Enrico Simonotto, Massimo Riani, Charles Seife, Mark Roberts, Jennifer Twitty, e Frank Moss <ref name=visual_percp> Physical Review Letters, Volume 78, numero 6, fevereiro de 1997 - Visual Perception of Stochastic Resonance - Enrico Simonotto, Massimo Riani, Charles Seife, Mark Roberts, Jennifer Twitty, and Frank Moss</ref> que discute os efeitos da RE na percepção visual. Em busca de um critério quantitativo objetivo, optaram por usar, em vez de imagens naturais, sinais 1D com regiões de frequência definível. | |||
Aos participantes do estudo foram mostradas imagens contendo faixas de “reconstituição” do sinal a partir de linhas construídas por diferentes realizações do ruído, como se vê na faixa da animação 2. A diferença principal é que em vez de atualizar uma linha por vez, toda a faixa era atualizada 60 vezes por segundo. Cada imagem continha sete faixas, cada faixa sendo elaborada a partir de um sinal da forma <math>A\sen(1/x) + 128</math> , com <math>\delta = 150</math> e diferentes amplitudes de A, como 28 ou 128. Além disso, todas as faixas eram submetidas a um ruído de mesma intensidade (mesmo desvio padrão), que variava a cada aplicação do teste. | |||
O teste consistia em pedir para o participante contar até que faixa (ou seja, para qual amplitude mínima) era capaz de discernir uma dada estrutura, efetivamente permitindo a construção de um gráfico de amplitude mínima vs intensidade do ruído. | |||
A animação 3 foi construída baseada nesse princípio, para efeito ilustrativo. A faixa mais acima seria uma representação ideal (em tons de cinza, 8 bits) do sinal com amplitude de 256. As demais têm amplitudes que vão diminuindo de baixo para cima. O limiar de corte e a intensidade do ruído são os mesmos para todas as faixas, sendo que o desvio padrão do ruído vai aumentando com o tempo: | |||
[[Arquivo:GIF3_RE.gif|frame|400x400px|center|Animação 3: Várias realizações de ruídos com diferentes desvios padrão, sobre uma sequência de faixas de um sinal com diferença apenas de amplitude e sob o mesmo limiar. A faixa do topo representa um sinal “idealmente representado” em tons de cinza e com amplitude de 256.]] | |||
O estudo encontrou, de fato, para cada participante, uma curva que aponta um nível ideal de ruído: quanto menos aparecem algumas estruturas, mais o ruído começa a dominar a imagem. Esse efeito, que é perceptível na animação 3, ajuda a justificar o termo ressonância estocástica. Curiosamente, a diferença entre as curvas encontradas para cada participante pôde ser justificada por uma simples constante multiplicativa. Essa constante variou muito pouco mediante repetições do teste pelo mesmo participante, mesmo com o espaçamento de semanas entre as repetições, sugerindo uma possível medida objetiva da capacidade de percepção desse tipo de estímulo visual. | |||
Outro ponto levantado pelo estudo, que pode ser conferido por uma comparação entre as animações 2 e 3, é que o efeito temporal acentuou a capacidade de percepção em relação às imagens estáticas das realizações do ruído. | |||
== Sistema biestável == | |||
O sistema biestável é um sistema em que uma partícula livre de movimento browniano está confinada em um potencial de duplo poço (figura 4). As regiões de estabilidade do sistema são dentro dos poços que são separados por uma barreira de potencial <math>(\Delta V)</math>. A partícula está sujeita a forças flutuantes que são induzidas, por exemplo, por um banho térmico. Tais forças flutuantes podem induzir a transição da partícula entre os dois estados a uma taxa conhecida como taxa de Kramer <math>(r_{k})</math>. A intensidade do ruído <math>(D)</math>, neste caso, está diretamente relacionado a temperatura <math>D = k_{b}T</math>. | |||
[[Arquivo:Potencial_biestavel.png|frame|297x232px|center|Figura 4: Potencial biestável. <ref name=stc_res/>]] | |||
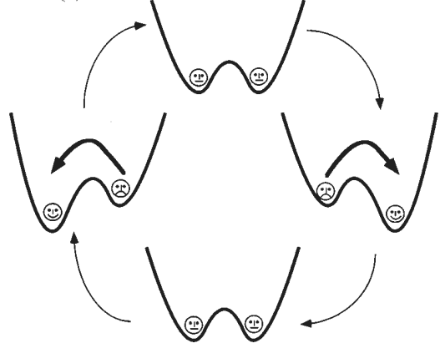
Caso haja uma força periódica no sistema, o potencial de poço duplo é influenciado pela força e, então, é alterado conforme o período da mesma. A aplicação da força inclina as barreiras de potencial dos poços da direita e esquerda de forma assimétrica, alterando a energia dos poços periodicamente (figura 5). | |||
[[Arquivo:Potencial_biestavel_inclinado.png|frame|297x232px|center|Figura 5: Inclinação do potencial biestável pela força periódica. <ref name=stc_res/>]] | |||
=== Modelo genérico === | |||
Considerando uma partícula browniana em um potencial biestável na presença de ruído e uma força periódica, tem-se a seguinte equação que rege a posição da partícula: | |||
<math> \frac{dx}{dt} = -V'(x) + A_{0} \cos(\Omega t + \phi) + \xi (x) </math> | |||
Em que <math>V(x)</math> é o potencial biestável da figura 4 que possui os mínimos em <math> \pm x_m </math> e centrado em <math> x_b. </math> | |||
<math> V(x) = -\frac{a}{2}x^2 + \frac{b}{4}x^4 </math> | |||
De forma que <math> \xi (x) </math> é um ruído branco gaussiano, centrado em zero e com função de autocorrelação | |||
<math> <\xi (t) \xi (0)> = 2D\delta (t) </math> | |||
e intensidade D. | |||
==== Sistema sem ruído e sem força periódica ==== | |||
Resolvendo a equação diferencial estocástica para um sistema sem ruído <math>(D = 0)</math> e sem força periódica <math>(A_0 = 0)</math>, obtém-se (figura 6): | |||
[[Arquivo:Sem_nada.png|frame|450x350px|center|Figura 6: Posição da partícula no poço sem ruído e sem força periódica.]] | |||
Nesta caso, como não há nenhum tipo de força aplicada na partícula, ela se mantém constante na posição de mínimo do poço <math>(x_m = 2)</math> e sem oscilação dentro do poço. | |||
==== Sistema sem ruído e com força periódica ==== | |||
Para o sistema sem ruído <math>(D = 0)</math> e com força periódica <math>(A_0 \neq 0)</math>, obtém-se (figura 7): | |||
[[Arquivo:Sem_ruido_com_forca1.png|frame|450x350px|center|Figura 7: Posição da partícula no poço sem ruído e com força periódica.]] | |||
Com a adição da força periódica, o sistema ganha energia para oscilar em torno da posição de menor energia do poço, entretanto a partícula não transita entre os estados do poço. | |||
==== Sistema com ruído e com força periódica ==== | |||
Para o sistema com ruído <math>(D \neq 0)</math> e com força periódica <math>(A_0 \neq 0)</math>, obtém-se (Figura 8): | |||
[[Arquivo:Com_ruido_forca.png|frame|450x350px|center|Figura 8: Posição da partícula no poço com ruído e com força periódica.]] | |||
Com a adição do ruído, o sistema transita entre os dois estados de menor energia do poço <math>(x_m = \pm 2)</math>, assim o ruído desempenha um papel fundamental na taxa de transição entre os estados (taxa de Kramer), como pode ser visto a seguir. | |||
=== Taxa de Kramer <math>(r_{k})</math> === | |||
A taxa de Kramer é a taxa de transição da partícula entre os estados de mínima energia do poço. Para um sistema sem força periódica, a taxa é dada por: | |||
<math>r_{k} = \frac{1}{\sqrt(2)\pi} \exp \left(\frac{-\Delta V}{D}\right)</math> | |||
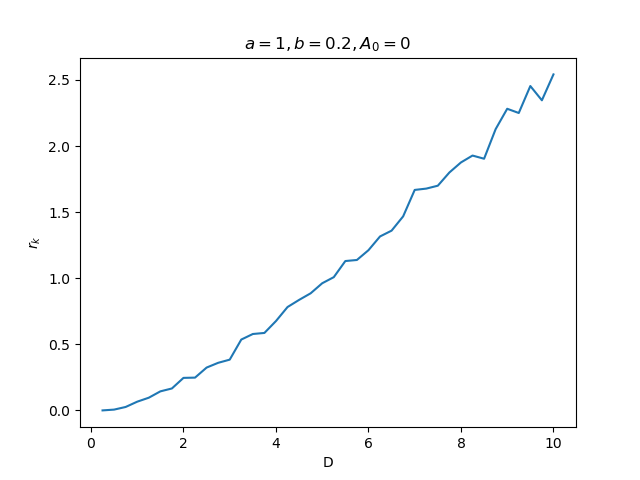
Como mencionado anteriormente, a taxa de Kramer depende da intensidade do ruído (Figura 9). | |||
[[Arquivo:Taxa_Kramer1.png|frame|450x350px|center|Figura 9: Dependência da taxa de Kramer com a intensidade do ruído.]] | |||
Quanto maior o ruído inserido no sistema, mais energia é fornecida para a partícula e, então, a taxa de Kramer é maior, como esperado pela equação acima. | |||
=== Outras medidas relevantes === | |||
O fenômeno de ressonância estocástica pode ser observado de outras formas além das médias sobre as realizações dos ruídos, como, por exemplo, pode ser quantificado através de observáveis facilmente mensuráveis e de alta relevância técnica. Os quais serão abordados nos próximos tópicos. | |||
==== Relação Sinal-Ruído ==== | |||
Entre elas existe a razão sinal-ruído, utilizada aqui sobre a seguinte definição: | |||
<math> SNR = 2 \left[\lim_{\Delta \omega \to 0}\int_{\Omega - \Delta \omega}^{\Omega + \Delta \omega} S(\omega)d\omega\right] / {S_N (\Omega)} </math> | |||
Onde <math>S(\omega)</math> é a densidade espectral em relação a posição <math>x(t)</math> da partícula. Sendo composta pela superposição da densidade espectral de fundo (background) e de uma estrutura de deltas centrados nos harmônicos ímpares <math> (\omega = (2n + 1)\Omega) </math> da frequência periódica do sistema <math>(\Omega).</math> | |||
Na figura 10 há um espectro de SNR padrão para um sistema biestável. <ref name=stc_res/> | |||
[[Arquivo:SNR.png|frame|450x350px|center|Figura 10: SNR padrão de um sistema biestável. <ref name=stc_res/>]] | |||
Onde <math>\nu</math> pode ser calculado de <math> \omega = 2\pi\nu. </math>. Percebe-se, na figura 10, os picos centrados nos harmônicos ímpares da frequência periódica do sistema. | |||
==== Distribuição do tempo de residência ==== | |||
O tempo de residência é o tempo entre duas transições subsequentes entre os dois estados do poço de potencial. Exemplo: Se a partícula transita para o estado positivo no tempo <math> t_i </math> e, depois, transita novamente para o estado negativo no tempo <math> t_j </math>, o tempo de residência é dado por: <math> T(s) = t_j - t_i.</math> | |||
Como as partículas podem transitar em diferentes tempos com probabilidades distintas, para uma realização tem-se uma distribuição de tempos de residência. | |||
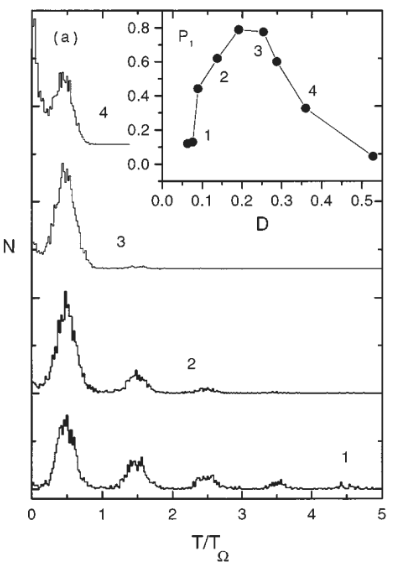
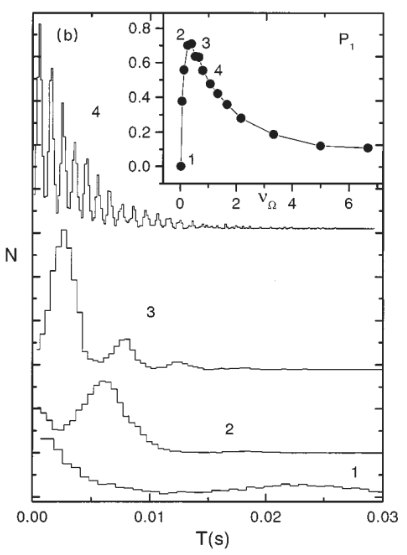
Em um sistema com uma força periódica, a distribuição é composta de uma série de picos centrados nos seguintes multiplos do período da força periódica <math>(T_{\Omega} = 2\pi/\Omega)</math>, que são: <math>T_n = (n-\frac{1}{2})T_\Omega</math> para <math>n</math> natural (figura 11). | |||
[[Arquivo:time_dist1.png|frame|450x350px|center|]] | |||
[[Arquivo:time_dist2.png|frame|450x350px|center|Figura 11: Distribuição do tempo de residência e anexo da variação de P1 com D. <ref name=stc_res/>]] | |||
A altura dos picos decai conforme <math>n</math> aumenta. Isso pode ser entendido em função da inclinação do potencial, pois é mais provável que ocorra uma mudança do estado 1 para o estado 2 quando o estado 2, através da influência da força periódica, for um mínimo global do sistema. Caso haja uma transição nesse momento, a partícula demorará, em média, metade do período da força periódica <math>(T_\Omega/2)</math> para transitar novamente, no momento de tempo em que a barreira assume um mínimo de potencial. Caso a partícula não transite nesse tempo, deverá esperar, no mínimo, outro período para a nova transição, ou seja, <math>3/2T_\Omega.</math> Desta maneira, forma-se o padrão da figura 11. | |||
Esse espectro pode ser utilizado para encontrar o nível de sincronismo entre a força periódica e a transição entre os mínimos. Por exemplo, se o tempo de residência for muito maior do que o período da força, provavelmente não haverá tempo para ocorrerem muitas transições primeiro período de mínimo, obtendo-se uma distribuição com mais picos. Por outro lado, se o tempo de residência for muito curto em comparação ao período, haverá tempo suficiente para a maioria das transições acontecerem no primeiro período, ou seja, a altura desse pico será maior e terá uma quantidade menor de picos totais. Esse comportamento pode ser observado nos gráficos anexos (internos) da figura 11, onde <math>P1</math> é a intensidade do primeiro pico. | |||
A máxima sincronização, maximização de <math>P1</math>, pode ser encontrada com a variação tanto de <math>D</math> como <math>\Omega</math>, o que possibilita outra forma de analisar a ressonância estocástica do sistema. | |||
==== Distribuição do tempo de residência - simulação ==== | |||
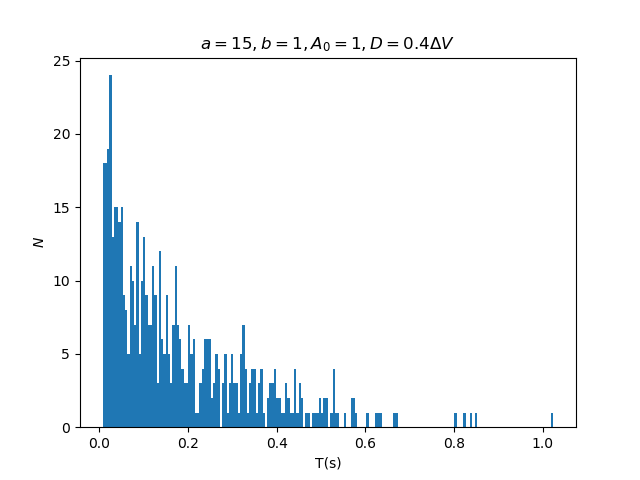
Para o modelo genérico apresentado anteriormente, a distribuição do tempo de residência pode ser visto na figura 12: | |||
[[Arquivo:time_dist_simulado.png|frame|450x350px|center|Figura 12: Distribuição do tempo de residência do modelo genérico de duplo poço.]] | |||
Percebe-se a semelhança entre o modelo genérico simulado com a distribuição da literatura <ref name=stc_res/>, em que há picos espaçados e decaindo em intensidade conforme o aumento do tempo de residência. | |||
== Aplicações == | |||
=== Era do gelo === | |||
Apesar do campo de pesquisa em RE ter surgido no contexto do estudo do período entre as eras glaciais e ter crescido bastante em muitas direções, as aplicações na climatologia se desenvolveram inicialmente de forma lenta <ref name=eras2/>. E “há várias falhas na descrição dos ciclos glaciais como uma simples ressonância estocástica”. <ref name=eras1/> | |||
Ainda assim, resultados interessantes foram encontrados na área ao longo do tempo. | |||
Há aproximadamente 1 milhão de anos, o período do ciclo glacial passou de 41 mil anos, alinhado ao ciclo de obliquidade da Terra, para 100 mil anos, alinhado ao ciclo de excentricidade da órbita da Terra, muito mais fraco. Um modelo foi encontrado usando RE que é consistente com essas transições. <ref name=eras1/> | |||
Outro efeito interessante são os eventos de calor de Dansgaard-Oeschger, que dizem respeito a picos bastante abruptos de calor (relativo) observados durante a última era glacial. Esses eventos também parecem poder ser explicados com ressonância estocástica, com eras do gelo tendo acesso a estados excitados mais quentes e o oceano atlântico agindo como sistema não linear amplificador: segundo <ref name=eras3> RGANOPOLSKI, Andrey; RAHMSTORF, Stefan. Rapid changes of glacial climate simulated in a coupled climate model. Nature, v. 409, n. 6817, p. 153, 2001.</ref>, “de fato, quando esse modelo climático é realizado com ruído aleatório de amplitude realista, combinado com um ciclo climático bastante fraco de 1500 anos, resultam eventos de Dansgaard-Oeschger que são muito similares àqueles gravados no gelo da Groenlândia e em outros arquivos paleo-climáticos.” <ref name=eras2/> | |||
=== Outras aplicações === | |||
A RE, em seus diferentes tipos, recebeu aplicações em uma vasta gama de áreas de estudo. Além da climatologia, do tratamento de sinais e dos lasers biestáveis, já citados, de semi-condutores e reações químicas, alguns outros exemplos são: | |||
- Há uma espécie de peixe de água doce (o “paddle fish”) que detecta plâncktons através de suas fracas emissões elétricas neurológicas. Esse efeito é acentuado por níveis apropriados de ruído elétrico. <ref name=fish> Russell, D.F., Wilkens, L.A. and Moss, F., 1999. Use of behavioural stochastic resonance by paddle fish for feeding. Nature, 402(6759), p.291.</ref> <ref name=eras2/> | |||
- Lagostins (“crayfish”) são crustáceos que lembram pequena lagostas. Eles têm um fotoreceptor caudal que exibe RE. <ref name=crayfish> Bahar, S. and Moss, F., 2004. Stochastic resonance and synchronization in the crayfish caudal photoreceptor. Mathematical biosciences, 188(1-2), pp.81-97.</ref> | |||
- Humanos detectam pequenos contatos táteis periódicos em seus dedos (do pé e da mão) melhor quando um nível apropriado de toques aleatórios é adicionado. <ref name=tactile> COLLINS, James J.; IMHOFF, Thomas T.; GRIGG, Peter. Noise-enhanced tactile sensation. Nature, 1996.</ref> <ref name=eras2/> | |||
- Sinais neurais são estocásticos. Em um experimento de 2013 foi adicionado um “ruído” periódico a sinais neurais estocásticos, o que resultou em melhoria na detecção dos sinais. Esse fenômeno foi chamado de um processo “reverso” de RE, já que um sinal coerente fraco foi adicionado para possibilitar a detecção de um sinal estocástico preexistente. A frequência ideal a ser adicionada foi encontrada em aproximadamente 190 hz: a mesma utilizada em tratamentos de Parkinson por altas frequências (2013, IEEE). <ref name=hippo> Durand, D.M., Kawaguchi, M. and Mino, H., 2013, July. Reverse stochastic resonance in a hippocampal CA1 neuron model. In 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) (pp. 5242-5245). IEEE.</ref> | |||
== Códigos == | |||
[https://github.com/deomar/metcompC/blob/master/RE_limiar.c Percepção visual - Ressonância estocástica em limiar] | |||
- | [https://github.com/deomar/metcompC/blob/master/RE_faixas.c Percepção visual - Ressonância estocástica em faixas com variação de ruído e amplitude] | ||
[https://github.com/deomar/metcompC/blob/master/Programa_posicao.py Modelo genérico - Simulação da posição da partícula dentro do poço] | |||
[https://github.com/deomar/metcompC/blob/master/taxa_kramer.py Modelo genérico - Cálculo da taxa de Kramer] | |||
[https://github.com/deomar/metcompC/blob/master/distribuicao_residencia.py Modelo genérico - Cálculo da distribuição dos tempos de residência] | |||
== Bibliografia == | |||
<references/> | |||
Edição atual tal como às 09h18min de 9 de janeiro de 2020
Introdução
A ressonância estocástica (RE) é o fenômeno em sistemas não-lineares em que sinais fracos podem ser amplificados e otimizados por um ruído branco, sendo o efeito encontrado em função do nível de ruído e de características do sistema e do sinal. [1]
Linear vs não linear
A concepção convencional é de que ruídos deterioram um sinal, oposto do que acontece na Ressonância Estocástica (RE). Um ponto chave para essa discrepância é a distinção entre sistemas lineares e não-lineares.
Em termos gerais, em sistemas lineares, a combinação de duas entradas resulta em uma saída equivalente à combinação das saídas que o sistema daria para cada entrada separada. [2] Ou seja, para uma função linear, se e , então .
Sistemas não-lineares, por outro lado, são todos aqueles que não são lineares. [2] É de se esperar que em sistemas lineares a adição de ruído possa apenas degradar ou mascarar um sinal inicial (o exemplo mais simples é a soma direta do ruído ao sinal). A RE é, portanto, um processo próprio de sistemas não-lineares. A não-linearidade, contudo, não é condição suficiente para que o fenômeno ocorra.
Condições para RE: Em geral, são condições necessárias para RE: [1]
- Barreira/limiar: um “obstáculo” à percepção de um sinal ou ao acontecimento de um evento. Um exemplo simples seria o efeito de “delta” em: , se ; , se
- Sinal fraco coerente: um sinal (entrada) que obedeça certo padrão e não seja, em geral, capaz de “superar” a barreira ou limiar associado ao sistema. O sentido físico dessa “superação” depende do sistema. Seguindo o exemplo anterior, essa condição seria satisfeita se fosse verdade para todo , por exemplo.
- Fonte de ruído não correlacionado (ou “ruído branco”): um sinal estocástico não-autocorrelacionado, de média zero, que não carrega informação senão por sua intensidade, que é a mesma para todas as frequências (no caso de um ruído branco gaussiano, está ligada ao desvio padrão).
Breve apanhado histórico
- Primeiras verificações eperimentais: Em tradução livre de [1]: ”Uma primeira verificação experimental do fenômeno de ressonância estocástica foi obtida por Fauve e Heslot (1983), que estudaram como a linha espectral de um gatilho de Schmitt dependia do ruído. O campo permaneceu então meio adormecido até a era moderna da ressonância estocástica até ser introduzida por um experimento chave em um ring laser biestável (McNamara, Wiesenfeld, e Roy, 1988).”
- Proposta Inicial: A primeira proposta para o fenômeno da RE foi elaborada pouco antes, a partir de 1981, no contexto do estudo sobre eras do gelo [Benzi et al., 1981, 1982, 1983] [1].
Foi observado que as eras glaciais aconteciam com um período da ordem de anos, sendo a variação da excentricidade orbital da Terra o único fenômeno cosmológico relevante com período em ordem comparável. Essas variações, contudo, representam uma diferença de no máximo 0,1% no fluxo de entrada de energia solar na superfície da Terra, o que a princípio não seria suficiente para explicar o fenômeno das eras glaciais.
A solução proposta modelava o sistema como tendo dois locos de estabilidade para temperaturas da Terra (essencialmente os estados “em era do gelo” ou “não em era do gelo”, com uma “barreira” entre eles), uma pequena variação periódica da insolação devido à excentricidade (“sinal”) e variações “aleatórias” anuais de temperatura (“ruído”). A existência das eras do gelo, com sua periodicidade, seria então explicada pelo fenômeno de RE. [1] Sistemas assim são chamados biestáveis.
Essa proposta de modelagem acabou por se mostrar limitada [3][4], mas o fenômeno, além das confirmações experimentais já citadas, foi aplicado com sucesso numa grande diversidade de áreas, inclusive no estudo das eras glaciais.
- Outros tipos de RE: Após a proposta do primeiro modelo, classificado como biestável por ter dois locos de estabilidade, mais dois tipos importantes de processos de RE começaram a ser estudados: os detectores de limiar e os excitáveis.
Os excitáveis estão relacionados a sistemas com um único estado estável, mas que contam também com um estado excitado de decaimento lento (se comparado à taxa de relaxamento de pequenas perturbações em torno do estado estável).
O exemplo dado na introdução, adicionado de um filtro 1 ou 0, pode ser usado para visualizar a RE de limiar. Em particular, de forma direta, pode ser usado para exemplificar o efeito da RE na percepção humana de sinais visuais com certas características, como veremos em detalhes a seguir. Sistemas excitáveis e de detecção de limiar acabaram por encontrar aplicação em outros campos, como na neurofisiologia de lagostins. [1]
Ressonância estocástica em detectores de limiar
Primeiras noções
Tomemos inicialmente um sinal com uma intensidade dada em função de uma posição , ou seja, , sujeito, para todo , a um limiar de detecção . A saída do nosso sistema será, para cada , 1 ou 0 (representados por “branco” ou “preto”) , correspondendo apenas à informação de se o sinal cruzou ou não o limiar - a diferença exata não importa.
Podemos imaginar três casos:
para todo , em que o sinal “some”.
para todo , em que observa-se que o sinal existe e ultrapassa o limiar em todos pontos, mas não temos ideia de sua estrutura interna para além disso.
com algumas regiões acima de e outras abaixo, onde temos um pouco de informação sobre parte dessa estrutura, mas não de forma geral.
A RE pode ajudar a reconstruir a informação do sinal nos três casos, mas nos exemplos a seguir nos focaremos inicialmente no primeiro, representado na figura 1.
O sinal (curva na parte inferior da imagem) não cruza o limiar (linha horizontal tracejada) e, portanto, não há nenhuma ativação.
A adição de uma constante ao sinal essencialmente nos leva para o caso 3, ainda não satisfatório, representado na figura 2.
A região cinza representa a “elevação” do sinal, enquanto a região escura localizada na parte superior indica que houve passagem naquelas posições. Finalmente, na figura 3, adicionamos uma realização de “ruído branco” gaussiano, de média zero, ao sinal original:
Nota-se que a densidade de barras verticais parece ter alguma relação com a forma do sinal original.
Percepção visual
- Reconstruindo o sinal original: Realizando o ruído diversas vezes e guardando a informação da quantidade de passagens para cada posição, pode-se estudar a proporção entre o número de passagens e o de realizações. A faixa superior da animação 1 mostra esse comportamento para , com 100% = branco e 0% = preto:
O que acontece é que a natureza da distribuição gaussiana faz com que mesmo pontos muito distantes do limiar possam superá-lo, mas com uma probabilidade menor, a cada realização, em relação à de que outros pontos mais próximos o façam. Como o ruído não guarda autocorrelação, o que acontece com cada ponto em cada realização é independente dos outros, mas a relação entre as probabilidades de cruzamento para cada ponto são constantes e definidas, dependendo apenas do desvio padrão do ruído e da intensidade do sinal em cada ponto.
Ao tomar a média, contudo, o resultado é trazido de volta a um espaço de tons de cinza, em vez do espaço binário preto e branco. Uma alternativa ao cálculo dessa proporção seria simplesmente guardar os diferentes resultados de cada realização, codificados da mesma forma anterior, nas diferentes linhas da faixa superior. A animação 2 mostra o resultado desse processo.
Nota-se que o efeito se mantém: com algumas poucas realizações já é possível, pela percepção visual, estimar detalhes do original. Além da economia de operações, esse sinal reconstruído se mantém binário: representa mais diretamente o que acontece com o sistema e pode, sem compressão, ser codificado em um arquivo de computador usando 1bit por pixel, em vez dos 8 bits por pixel normalmente usados em imagens em tons de cinza (também sem compressão).
Imaginando um sinal 2D, pode-se encontrar uma ligação entre o efeito visto e o processo de dithering [5], que em uma imagem visa justamente diminuir sua paleta de cores mantendo o máximo da percepção de sua informação original.
- O efeito da ressonância estocástica na percepção visual: Em 1997 foi publicado um artigo de Enrico Simonotto, Massimo Riani, Charles Seife, Mark Roberts, Jennifer Twitty, e Frank Moss [6] que discute os efeitos da RE na percepção visual. Em busca de um critério quantitativo objetivo, optaram por usar, em vez de imagens naturais, sinais 1D com regiões de frequência definível.
Aos participantes do estudo foram mostradas imagens contendo faixas de “reconstituição” do sinal a partir de linhas construídas por diferentes realizações do ruído, como se vê na faixa da animação 2. A diferença principal é que em vez de atualizar uma linha por vez, toda a faixa era atualizada 60 vezes por segundo. Cada imagem continha sete faixas, cada faixa sendo elaborada a partir de um sinal da forma , com e diferentes amplitudes de A, como 28 ou 128. Além disso, todas as faixas eram submetidas a um ruído de mesma intensidade (mesmo desvio padrão), que variava a cada aplicação do teste.
O teste consistia em pedir para o participante contar até que faixa (ou seja, para qual amplitude mínima) era capaz de discernir uma dada estrutura, efetivamente permitindo a construção de um gráfico de amplitude mínima vs intensidade do ruído. A animação 3 foi construída baseada nesse princípio, para efeito ilustrativo. A faixa mais acima seria uma representação ideal (em tons de cinza, 8 bits) do sinal com amplitude de 256. As demais têm amplitudes que vão diminuindo de baixo para cima. O limiar de corte e a intensidade do ruído são os mesmos para todas as faixas, sendo que o desvio padrão do ruído vai aumentando com o tempo:
O estudo encontrou, de fato, para cada participante, uma curva que aponta um nível ideal de ruído: quanto menos aparecem algumas estruturas, mais o ruído começa a dominar a imagem. Esse efeito, que é perceptível na animação 3, ajuda a justificar o termo ressonância estocástica. Curiosamente, a diferença entre as curvas encontradas para cada participante pôde ser justificada por uma simples constante multiplicativa. Essa constante variou muito pouco mediante repetições do teste pelo mesmo participante, mesmo com o espaçamento de semanas entre as repetições, sugerindo uma possível medida objetiva da capacidade de percepção desse tipo de estímulo visual.
Outro ponto levantado pelo estudo, que pode ser conferido por uma comparação entre as animações 2 e 3, é que o efeito temporal acentuou a capacidade de percepção em relação às imagens estáticas das realizações do ruído.
Sistema biestável
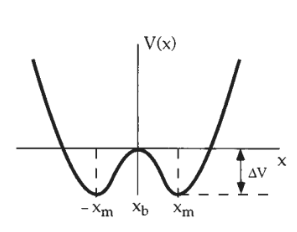
O sistema biestável é um sistema em que uma partícula livre de movimento browniano está confinada em um potencial de duplo poço (figura 4). As regiões de estabilidade do sistema são dentro dos poços que são separados por uma barreira de potencial . A partícula está sujeita a forças flutuantes que são induzidas, por exemplo, por um banho térmico. Tais forças flutuantes podem induzir a transição da partícula entre os dois estados a uma taxa conhecida como taxa de Kramer . A intensidade do ruído , neste caso, está diretamente relacionado a temperatura .
Caso haja uma força periódica no sistema, o potencial de poço duplo é influenciado pela força e, então, é alterado conforme o período da mesma. A aplicação da força inclina as barreiras de potencial dos poços da direita e esquerda de forma assimétrica, alterando a energia dos poços periodicamente (figura 5).
Modelo genérico
Considerando uma partícula browniana em um potencial biestável na presença de ruído e uma força periódica, tem-se a seguinte equação que rege a posição da partícula:
Em que é o potencial biestável da figura 4 que possui os mínimos em e centrado em
De forma que é um ruído branco gaussiano, centrado em zero e com função de autocorrelação
e intensidade D.
Sistema sem ruído e sem força periódica
Resolvendo a equação diferencial estocástica para um sistema sem ruído e sem força periódica , obtém-se (figura 6):
Nesta caso, como não há nenhum tipo de força aplicada na partícula, ela se mantém constante na posição de mínimo do poço e sem oscilação dentro do poço.
Sistema sem ruído e com força periódica
Para o sistema sem ruído e com força periódica , obtém-se (figura 7):
Com a adição da força periódica, o sistema ganha energia para oscilar em torno da posição de menor energia do poço, entretanto a partícula não transita entre os estados do poço.
Sistema com ruído e com força periódica
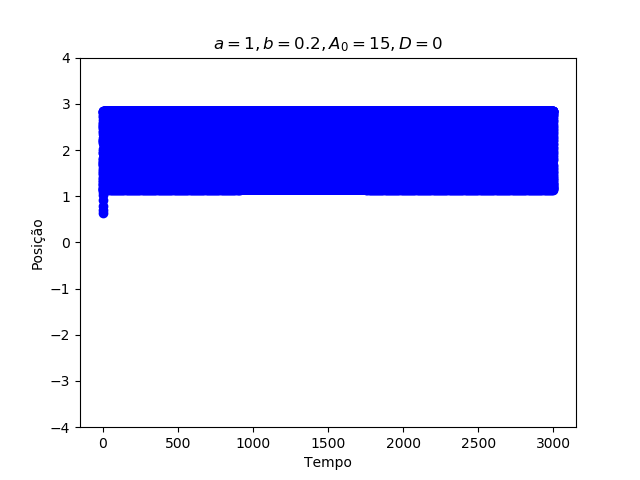
Para o sistema com ruído e com força periódica , obtém-se (Figura 8):
Com a adição do ruído, o sistema transita entre os dois estados de menor energia do poço , assim o ruído desempenha um papel fundamental na taxa de transição entre os estados (taxa de Kramer), como pode ser visto a seguir.
Taxa de Kramer
A taxa de Kramer é a taxa de transição da partícula entre os estados de mínima energia do poço. Para um sistema sem força periódica, a taxa é dada por:
Como mencionado anteriormente, a taxa de Kramer depende da intensidade do ruído (Figura 9).
Quanto maior o ruído inserido no sistema, mais energia é fornecida para a partícula e, então, a taxa de Kramer é maior, como esperado pela equação acima.
Outras medidas relevantes
O fenômeno de ressonância estocástica pode ser observado de outras formas além das médias sobre as realizações dos ruídos, como, por exemplo, pode ser quantificado através de observáveis facilmente mensuráveis e de alta relevância técnica. Os quais serão abordados nos próximos tópicos.
Relação Sinal-Ruído
Entre elas existe a razão sinal-ruído, utilizada aqui sobre a seguinte definição:
Onde é a densidade espectral em relação a posição da partícula. Sendo composta pela superposição da densidade espectral de fundo (background) e de uma estrutura de deltas centrados nos harmônicos ímpares da frequência periódica do sistema Na figura 10 há um espectro de SNR padrão para um sistema biestável. [1]

Onde pode ser calculado de . Percebe-se, na figura 10, os picos centrados nos harmônicos ímpares da frequência periódica do sistema.
Distribuição do tempo de residência
O tempo de residência é o tempo entre duas transições subsequentes entre os dois estados do poço de potencial. Exemplo: Se a partícula transita para o estado positivo no tempo e, depois, transita novamente para o estado negativo no tempo , o tempo de residência é dado por:
Como as partículas podem transitar em diferentes tempos com probabilidades distintas, para uma realização tem-se uma distribuição de tempos de residência. Em um sistema com uma força periódica, a distribuição é composta de uma série de picos centrados nos seguintes multiplos do período da força periódica , que são: para natural (figura 11).
A altura dos picos decai conforme aumenta. Isso pode ser entendido em função da inclinação do potencial, pois é mais provável que ocorra uma mudança do estado 1 para o estado 2 quando o estado 2, através da influência da força periódica, for um mínimo global do sistema. Caso haja uma transição nesse momento, a partícula demorará, em média, metade do período da força periódica para transitar novamente, no momento de tempo em que a barreira assume um mínimo de potencial. Caso a partícula não transite nesse tempo, deverá esperar, no mínimo, outro período para a nova transição, ou seja, Desta maneira, forma-se o padrão da figura 11.
Esse espectro pode ser utilizado para encontrar o nível de sincronismo entre a força periódica e a transição entre os mínimos. Por exemplo, se o tempo de residência for muito maior do que o período da força, provavelmente não haverá tempo para ocorrerem muitas transições primeiro período de mínimo, obtendo-se uma distribuição com mais picos. Por outro lado, se o tempo de residência for muito curto em comparação ao período, haverá tempo suficiente para a maioria das transições acontecerem no primeiro período, ou seja, a altura desse pico será maior e terá uma quantidade menor de picos totais. Esse comportamento pode ser observado nos gráficos anexos (internos) da figura 11, onde é a intensidade do primeiro pico.
A máxima sincronização, maximização de , pode ser encontrada com a variação tanto de como , o que possibilita outra forma de analisar a ressonância estocástica do sistema.
Distribuição do tempo de residência - simulação
Para o modelo genérico apresentado anteriormente, a distribuição do tempo de residência pode ser visto na figura 12:
Percebe-se a semelhança entre o modelo genérico simulado com a distribuição da literatura [1], em que há picos espaçados e decaindo em intensidade conforme o aumento do tempo de residência.
Aplicações
Era do gelo
Apesar do campo de pesquisa em RE ter surgido no contexto do estudo do período entre as eras glaciais e ter crescido bastante em muitas direções, as aplicações na climatologia se desenvolveram inicialmente de forma lenta [4]. E “há várias falhas na descrição dos ciclos glaciais como uma simples ressonância estocástica”. [3]
Ainda assim, resultados interessantes foram encontrados na área ao longo do tempo. Há aproximadamente 1 milhão de anos, o período do ciclo glacial passou de 41 mil anos, alinhado ao ciclo de obliquidade da Terra, para 100 mil anos, alinhado ao ciclo de excentricidade da órbita da Terra, muito mais fraco. Um modelo foi encontrado usando RE que é consistente com essas transições. [3]
Outro efeito interessante são os eventos de calor de Dansgaard-Oeschger, que dizem respeito a picos bastante abruptos de calor (relativo) observados durante a última era glacial. Esses eventos também parecem poder ser explicados com ressonância estocástica, com eras do gelo tendo acesso a estados excitados mais quentes e o oceano atlântico agindo como sistema não linear amplificador: segundo [7], “de fato, quando esse modelo climático é realizado com ruído aleatório de amplitude realista, combinado com um ciclo climático bastante fraco de 1500 anos, resultam eventos de Dansgaard-Oeschger que são muito similares àqueles gravados no gelo da Groenlândia e em outros arquivos paleo-climáticos.” [4]
Outras aplicações
A RE, em seus diferentes tipos, recebeu aplicações em uma vasta gama de áreas de estudo. Além da climatologia, do tratamento de sinais e dos lasers biestáveis, já citados, de semi-condutores e reações químicas, alguns outros exemplos são:
- Há uma espécie de peixe de água doce (o “paddle fish”) que detecta plâncktons através de suas fracas emissões elétricas neurológicas. Esse efeito é acentuado por níveis apropriados de ruído elétrico. [8] [4]
- Lagostins (“crayfish”) são crustáceos que lembram pequena lagostas. Eles têm um fotoreceptor caudal que exibe RE. [9]
- Humanos detectam pequenos contatos táteis periódicos em seus dedos (do pé e da mão) melhor quando um nível apropriado de toques aleatórios é adicionado. [10] [4]
- Sinais neurais são estocásticos. Em um experimento de 2013 foi adicionado um “ruído” periódico a sinais neurais estocásticos, o que resultou em melhoria na detecção dos sinais. Esse fenômeno foi chamado de um processo “reverso” de RE, já que um sinal coerente fraco foi adicionado para possibilitar a detecção de um sinal estocástico preexistente. A frequência ideal a ser adicionada foi encontrada em aproximadamente 190 hz: a mesma utilizada em tratamentos de Parkinson por altas frequências (2013, IEEE). [11]
Códigos
Percepção visual - Ressonância estocástica em limiar
Percepção visual - Ressonância estocástica em faixas com variação de ruído e amplitude
Modelo genérico - Simulação da posição da partícula dentro do poço
Modelo genérico - Cálculo da taxa de Kramer
Modelo genérico - Cálculo da distribuição dos tempos de residência
Bibliografia
- ↑ 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 Reviews of Modern Physics, Vol. 70, No. 1, January 1998 - Stochastic resonance - Luca Gammaitoni, Sezione di Perugia, Peter Hänggi, Peter Jung, and Fabio Marchesoni
- ↑ 2,0 2,1 MIT News, February 26, 2010 - “Explained: Linear and Nonlinear Systems” - Larry Hardesty - https://news.mit.edu/2010/explained-linear-0226
- ↑ 3,0 3,1 3,2 P.D. Ditlevsen, Chem. Phys. (2010), doi:10.1016/j.chemphys.2010.05.022 - Extension of stochastic resonance in the dynamics of ice ages - Peter D. Ditlevsen
- ↑ 4,0 4,1 4,2 4,3 4,4 Stochastic Resonance in Glacial Climate - Stefan Rahmstorf and Richard Alley - Revised Version, 17 December 2001
- ↑ Physical Review E, vol 61, number 1, jannuary 2000 - Stochastic resonance as dithering - Robert A. Wannamaker, Stanley P. Lipshitz, and John Vanderkooy
- ↑ Physical Review Letters, Volume 78, numero 6, fevereiro de 1997 - Visual Perception of Stochastic Resonance - Enrico Simonotto, Massimo Riani, Charles Seife, Mark Roberts, Jennifer Twitty, and Frank Moss
- ↑ RGANOPOLSKI, Andrey; RAHMSTORF, Stefan. Rapid changes of glacial climate simulated in a coupled climate model. Nature, v. 409, n. 6817, p. 153, 2001.
- ↑ Russell, D.F., Wilkens, L.A. and Moss, F., 1999. Use of behavioural stochastic resonance by paddle fish for feeding. Nature, 402(6759), p.291.
- ↑ Bahar, S. and Moss, F., 2004. Stochastic resonance and synchronization in the crayfish caudal photoreceptor. Mathematical biosciences, 188(1-2), pp.81-97.
- ↑ COLLINS, James J.; IMHOFF, Thomas T.; GRIGG, Peter. Noise-enhanced tactile sensation. Nature, 1996.
- ↑ Durand, D.M., Kawaguchi, M. and Mino, H., 2013, July. Reverse stochastic resonance in a hippocampal CA1 neuron model. In 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) (pp. 5242-5245). IEEE.










































![{\displaystyle SNR=2\left[\lim _{\Delta \omega \to 0}\int _{\Omega -\Delta \omega }^{\Omega +\Delta \omega }S(\omega )d\omega \right]/{S_{N}(\Omega )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85f2c2ed3e0de50d384b100de2967a9d994ec655)