Zeros de Funções: mudanças entre as edições
(Criou página com 'O problema aqui é encontrar os valores da variável independente <math>x_i</math> que fazem com a função <math>f(x_i)</math> tenha o valor zero.<br> Matematicamente pode ser f...') |
|||
| (5 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
tenha o valor zero. | |||
<!--- | |||
---> | |||
Calcular o zero de uma função significa encontrar os valores da variável independente <math>x_i</math> que fazem com que a função <math>f(x_i)</math> | |||
tenha o valor zero. | |||
Matematicamente pode ser formalizado assim: | Matematicamente pode ser formalizado assim: | ||
| Linha 19: | Linha 27: | ||
:<math>x = (-b +- \sqrt{b^2 - 4ac})/2a</math> | :<math>x = (-b +- \sqrt{b^2 - 4ac})/2a</math> | ||
Porém, quando a função é mais complicada, o problema de achar os zeros pode não ter (é o mais comum) | |||
solução analítica. | solução analítica. | ||
Vale notar que ao tratar dos ''zeros'' podemos generalizar o conceito para qualquer outro valor. | Vale notar que ao tratar dos ''zeros'' podemos generalizar o conceito para qualquer outro valor. | ||
Por exemplo, achar ''x'' tal que <math>f(x) = d</math> é equivalente a achar os zeros de <math>f(x)-d</math>. | Por exemplo, achar ''x'' tal que <math>f(x) = d</math> é equivalente a achar os zeros de <math>f(x)-d</math>. | ||
De outra forma podemos dizer que trata-se do problema '''inverso:''' dado o valor da função queremos saber | De outra forma podemos dizer que trata-se do problema '''inverso:''' dado o valor da função queremos saber a qual valor da variável independente ele corresponde. | ||
Numericamente, temos três métodos usuais que serão descritos aqui, os métodos da Iteração Simples, Newton-Raphson e Método da Bisecção. | |||
== Iteração Simples == | |||
Para o método da iteração simples, utiliza-se uma nova função <math>F(x)</math> para encontrar o zero da função original <math>f(x)</math>, de modo que se define | |||
O método de Newton-Raphson é um procedimento para encontrar zeros de funções de maneira iterativa. | :<math> F(x) = f(x) + x,</math> | ||
Partindo de um ponto qualquer da função vamos ao próximo ponto com deslocamento dado pela derivada no ponto inicial: | assim | ||
:<math> F(x) = x \,\; para \,\; f(x) = 0.</math> | |||
Utilizamos a própria função para definir o valor de <math>x</math> nas iterações, tendo que existir um "chute" inicial para o valor <math>x_0</math>. Assim, a iteração pode ser definida como | |||
:<math> x_{n+1} = F(x_n) </math>. | |||
Itera-se a equação até atingir-se um valor fixo, ou seja, <math>x_{n+1} = x_n </math>. | |||
As duas principais destavantagens deste método devem-se ao fato de ele ser mais lento que demais métodos e por existir funções que apresentam raízes "instáveis" de iteração. Ou seja, são raízes que este método não é capaz de encontrar. | |||
Para descobrir se haverá raízes instáveis de convergência, utilizamos a condição de convergência do método, perturbando a solução <math>x_{n+1} = x_n = x^*</math> e expandindo em série de Taylor: | |||
:<math>x^*+\delta = F(x^*+\delta) = F(x^*) + \frac{dF(x^*)}{dx}\delta+ ...</math> | |||
Note que para | |||
:<math>\|\frac{dF(x^*)}{dx}\| \leqslant 1</math> | |||
o efeito da perturbação decai, indicando que a raíz <math>x^*</math> é estável por este método. Ao contrário, se expressão acima for maior do 1, isto implica que uma pequena perturbação faria com que os valores da função se afastassem do valor de <math> F(x^*) </math> mesmo se estivéssemos calculando um valor da função em | |||
<math>x^*+\delta</math> com <math>\delta</math> muito pequeno. Se este for o caso, então o método de iteração simples não consegue encontrar a raiz | |||
<math>x^*</math>. | |||
[[Image:iterasimp.png|650px]] | |||
== Newton-Raphson == | |||
O método de '''Newton-Raphson''' é um procedimento para encontrar zeros de funções de maneira iterativa, assim como o método da iteração simples. Partindo de um ponto qualquer da função vamos ao próximo ponto com deslocamento dado pela derivada no ponto inicial: | |||
[[Image:newton.png|right|frame|Método de Newton-Raphson com <math>x_0</math> e <math>x_1</math>.]] | |||
:<math>f'(x_{n}) = \frac{ f( x_{n} ) - 0 }{ x_{n} - x_{n+1} } = \frac{0 - f(x_{n})}{(x_{n+1} - x_{n})}\,\!</math> | :<math>f'(x_{n}) = \frac{ f( x_{n} ) - 0 }{ x_{n} - x_{n+1} } = \frac{0 - f(x_{n})}{(x_{n+1} - x_{n})}\,\!</math> | ||
| Linha 36: | Linha 79: | ||
e o processo é repetido até a precisão desejada. | e o processo é repetido até a precisão desejada. | ||
Note que numericamente não temos garantia de achar exatamente a raiz. Devemos fixar um <math>\epsilon</math> | |||
que determina a tolerância com que vamos a aceitar o zero. Ou seja quando | que determina a tolerância com que vamos a aceitar o zero. Ou seja quando <math>|f(x)| < \epsilon</math> paramos a procura. | ||
<math>|f(x)| < \epsilon</math> paramos a procura. | |||
Por outra parte o método não garante a convergência, isto é, pode acontecer que o processo entre num ciclo infinito | Por outra parte o método não garante a convergência, isto é, pode acontecer que o processo entre num ciclo infinito | ||
pipocando de uma lado para outro da raiz, sem poder encontrar uma solução. | pipocando de uma lado para outro da raiz, sem poder encontrar uma solução. | ||
Geometricamente, como mostrado na figura ao lado, tendo sido escolhido o ponto <math>x_0</math>, queremos que o ponto <math>x_1</math> seja o encontro da reta tangente (ou da derivada) da função no ponto <math>x_0</math> com a reta das abcissas. Sendo | |||
:<math>f'(x_0)=tan(\theta)</math>, | |||
temos que | |||
:<math>x_0 - x_1 = \frac{f(x_0)}{f'(x_0)}</math>. | |||
A figura abaixo mostra as iterações do método de Newton-Raphson (retirado da Wikipedia [http://en.wikipedia.org/wiki/Newton's_method]) | |||
[[Imagem:newtoniteration.gif|500px|]] | |||
== Bissecção == | |||
O método da bissecção consiste em utilizar um intervalo de valores de <math>x</math> que é sabido que contenha uma raíz. Note que temos que ter uma noção prévia da função para utilizar este método. Definindo um intervalo | |||
:<math> a \leqslant x \leqslant b </math>, | |||
temos a condição <math>f(a)f(b) < 0 </math>, indicando que há pelo menos um zero contido neste intervalo, ou seja, que a função "corta" o eixo das abcissas, de modo que um valor da função seja maior que zero e outro menor. | |||
Definindo o intervalo inicial <math>[a,b]</math>, dividimos este por dois, encontrando o valor médio <math>x_m</math>, dado por | |||
:<math> x_m = a + \frac{b-a}{2} = \frac{a+b}{2}.</math> | |||
Note que estamos com dois intervalos de <math>x</math>, primeiro <math>[a,x_m]</math> e segundo <math>[x_m,b]</math>. Agora precisamos descobrir em qual desses dois intervalos há uma raíz. Para isso calculamos o produto das funções nos pontos específicos. Se <math>f(a)f(x_m)<0</math> e <math>f(x_m)f(b)>0</math>, continuamos com o primeiro intervalo (que contém um raíz), caso contrário com o segundo. Prosseguindo com o algoritmo, dividimos o novo intervalo que contém a raiz novamente | |||
:<math> x_{m2} = \frac{x_m+a}{2}.</math> | |||
Repetimos o processo anterior, verificando em qual dos dois novos intervalos, <math>[a,x_{m2}]</math> ou <math>[x_{m2},x_m]</math> está a raiz. | |||
O algoritmo é repetido até encontrarmos a raíz, com a precisão <math>\eta</math> ou seja, até que <math>-\eta^2 \leqslant f(a)f(b) \leqslant 0</math>. O ideal é ao final ficar com o valor intermediário das funções. | |||
Abaixo há uma figura com duas iterações do método da bissecção, assim como descrito acima. | |||
[[Imagem:bisseccao.png|800px|]] | |||
== Programação == | == Programação == | ||
| Linha 55: | Linha 134: | ||
else | else | ||
x = x - f(x)/g(x) | x = x - f(x)/g(x) | ||
if (f(x) < eps) then | if (abs(f(x)) < eps) then | ||
print*, " | print*, "raiz em x=", x, "f(x)=", f(x) | ||
exit | exit | ||
endif | endif | ||
Edição atual tal como às 07h35min de 9 de novembro de 2011
Calcular o zero de uma função significa encontrar os valores da variável independente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_i}
que fazem com que a função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_i)}
tenha o valor zero.
Matematicamente pode ser formalizado assim:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x : f(x) = 0\,}
Os zeros da função f são também chamados de raízes.
Um exemplo simples é achar as raízes da função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/(x + 1) - 2} . A simplicidade vem do fato dessa função ter inversa, com o qual a solução pode ser encontrada isolando o x: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = -1/2} que é o zero dessa função ou equação.
Outro exemplo clássico são as raízes de uma parábola:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)=ax^2+bx+c \,}
da qual existe uma expressão para as raízes (cuja programação é um dos exercícios):
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = (-b +- \sqrt{b^2 - 4ac})/2a}
Porém, quando a função é mais complicada, o problema de achar os zeros pode não ter (é o mais comum) solução analítica.
Vale notar que ao tratar dos zeros podemos generalizar o conceito para qualquer outro valor.
Por exemplo, achar x tal que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) = d}
é equivalente a achar os zeros de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)-d}
.
De outra forma podemos dizer que trata-se do problema inverso: dado o valor da função queremos saber a qual valor da variável independente ele corresponde.
Numericamente, temos três métodos usuais que serão descritos aqui, os métodos da Iteração Simples, Newton-Raphson e Método da Bisecção.
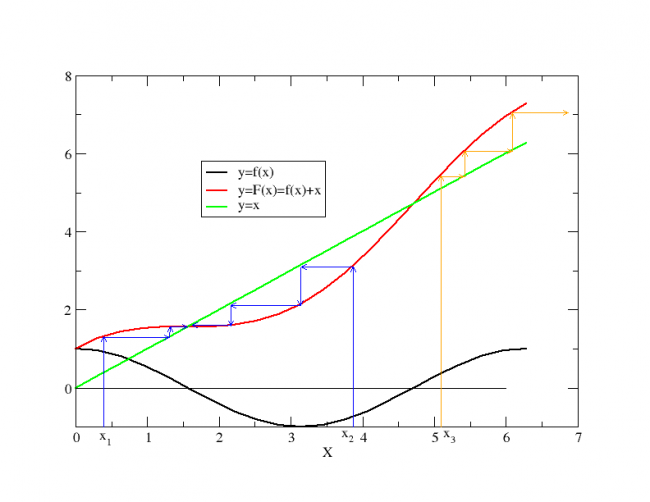
Iteração Simples
Para o método da iteração simples, utiliza-se uma nova função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x)} para encontrar o zero da função original Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} , de modo que se define
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x) = f(x) + x,}
assim
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x) = x \,\; para \,\; f(x) = 0.}
Utilizamos a própria função para definir o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} nas iterações, tendo que existir um "chute" inicial para o valor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} . Assim, a iteração pode ser definida como
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{n+1} = F(x_n) } .
Itera-se a equação até atingir-se um valor fixo, ou seja, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{n+1} = x_n } .
As duas principais destavantagens deste método devem-se ao fato de ele ser mais lento que demais métodos e por existir funções que apresentam raízes "instáveis" de iteração. Ou seja, são raízes que este método não é capaz de encontrar. Para descobrir se haverá raízes instáveis de convergência, utilizamos a condição de convergência do método, perturbando a solução Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{n+1} = x_n = x^*} e expandindo em série de Taylor:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^*+\delta = F(x^*+\delta) = F(x^*) + \frac{dF(x^*)}{dx}\delta+ ...}
Note que para
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \|\frac{dF(x^*)}{dx}\| \leqslant 1}
o efeito da perturbação decai, indicando que a raíz Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^*} é estável por este método. Ao contrário, se expressão acima for maior do 1, isto implica que uma pequena perturbação faria com que os valores da função se afastassem do valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x^*) } mesmo se estivéssemos calculando um valor da função em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^*+\delta} com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} muito pequeno. Se este for o caso, então o método de iteração simples não consegue encontrar a raiz Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^*} .
Newton-Raphson
O método de Newton-Raphson é um procedimento para encontrar zeros de funções de maneira iterativa, assim como o método da iteração simples. Partindo de um ponto qualquer da função vamos ao próximo ponto com deslocamento dado pela derivada no ponto inicial:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(x_{n}) = \frac{ f( x_{n} ) - 0 }{ x_{n} - x_{n+1} } = \frac{0 - f(x_{n})}{(x_{n+1} - x_{n})}\,\!}
Desta forma o próximo ponto está dado por:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\,\!} .
e o processo é repetido até a precisão desejada. Note que numericamente não temos garantia de achar exatamente a raiz. Devemos fixar um Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} que determina a tolerância com que vamos a aceitar o zero. Ou seja quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle |f(x)| < \epsilon} paramos a procura.
Por outra parte o método não garante a convergência, isto é, pode acontecer que o processo entre num ciclo infinito pipocando de uma lado para outro da raiz, sem poder encontrar uma solução.
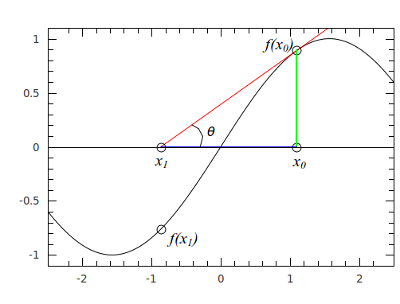
Geometricamente, como mostrado na figura ao lado, tendo sido escolhido o ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} , queremos que o ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1} seja o encontro da reta tangente (ou da derivada) da função no ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} com a reta das abcissas. Sendo
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(x_0)=tan(\theta)} ,
temos que
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0 - x_1 = \frac{f(x_0)}{f'(x_0)}} .
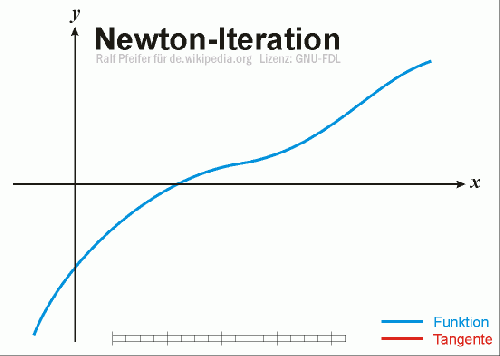
A figura abaixo mostra as iterações do método de Newton-Raphson (retirado da Wikipedia [1])
Bissecção
O método da bissecção consiste em utilizar um intervalo de valores de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} que é sabido que contenha uma raíz. Note que temos que ter uma noção prévia da função para utilizar este método. Definindo um intervalo
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a \leqslant x \leqslant b } ,
temos a condição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(a)f(b) < 0 } , indicando que há pelo menos um zero contido neste intervalo, ou seja, que a função "corta" o eixo das abcissas, de modo que um valor da função seja maior que zero e outro menor.
Definindo o intervalo inicial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a,b]} , dividimos este por dois, encontrando o valor médio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_m} , dado por
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_m = a + \frac{b-a}{2} = \frac{a+b}{2}.}
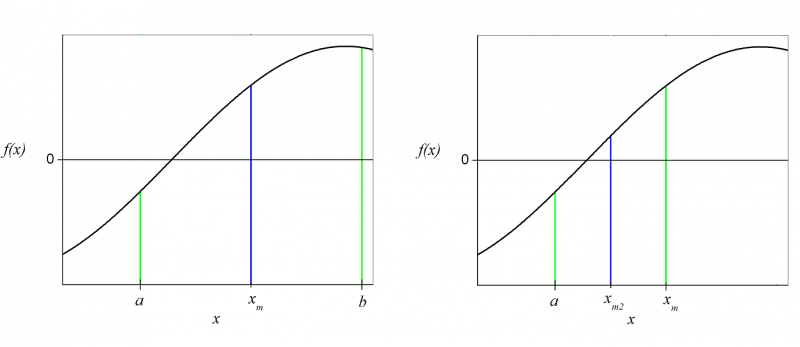
Note que estamos com dois intervalos de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} , primeiro Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a,x_m]} e segundo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [x_m,b]} . Agora precisamos descobrir em qual desses dois intervalos há uma raíz. Para isso calculamos o produto das funções nos pontos específicos. Se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(a)f(x_m)<0} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_m)f(b)>0} , continuamos com o primeiro intervalo (que contém um raíz), caso contrário com o segundo. Prosseguindo com o algoritmo, dividimos o novo intervalo que contém a raiz novamente
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{m2} = \frac{x_m+a}{2}.}
Repetimos o processo anterior, verificando em qual dos dois novos intervalos, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a,x_{m2}]} ou Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [x_{m2},x_m]} está a raiz.
O algoritmo é repetido até encontrarmos a raíz, com a precisão ou seja, até que . O ideal é ao final ficar com o valor intermediário das funções.
Abaixo há uma figura com duas iterações do método da bissecção, assim como descrito acima.
Programação
Para programá-lo em FORTRAN o mais prático é definir como funções tanto a própria função como a sua derivada. Sejam elas f(x) e g(x) respectivamente, o trecho de código com a implementação do método fica:
...
x = x0
Do
if (g(x)==0) then
print*, "em x=", x, "a derivada é zero"
else
x = x - f(x)/g(x)
if (abs(f(x)) < eps) then
print*, "raiz em x=", x, "f(x)=", f(x)
exit
endif
endif
endo
...
Plano Complexo
O método pode ser estendido a funções f(z) onde z, e f(z) pertencem a C (domínio dos números complexos). Dessa forma todas as raízes de um polinômio podem em princípio ser encontradas. O método tem a mesma formulação teórica. Só muda o programa pois precisamos usar complexos.
Complex f, z Real x,y Read*, x,y z = CMPLX(x,y) ! função FORTRAN intrínseca para converter un par x,y de variáveis reais numa variável complexa ... if (abs(f(z)<eps) print*, z ...