Mínimos Quadrados: mudanças entre as edições
(pequeno erro de grafia mas com significado) |
|||
| (2 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 181: | Linha 181: | ||
</pre> | </pre> | ||
=Ajuste ponderado= | =Ajuste ponderado= | ||
Dependendo da situação, convém fazer um ajuste levando em conta o erro associado a cada ponto, i.e., atribuindo maior peso para pontos com um erro baixo e menor peso para os pontos onde o erro é sabidamente maior. Ou seja, se definirmos <math>w_i</math> como o peso associado ao ponto <math>( | Dependendo da situação, convém fazer um ajuste levando em conta o erro associado a cada ponto, i.e., atribuindo maior peso para pontos com um erro baixo e menor peso para os pontos onde o erro é sabidamente maior. Ou seja, se definirmos <math>w_i</math> como o peso associado ao ponto <math>(x_i,y_i)</math>, gostaríamos que ele seja maior quanto menor for o erro associado a este ponto. | ||
Se <math>S_{y_i}</math> é o erro associado a este ponto, e considerando que o ajuste proposto é tal que minimiza a distância quadrática, podemos definir então <math>w_i</math> como: | Se <math>S_{y_i}</math> é o erro associado a este ponto, e considerando que o ajuste proposto é tal que minimiza a distância quadrática, podemos definir então <math>w_i</math> como: | ||
| Linha 218: | Linha 218: | ||
fonte de erro. Assim para ver como o erro neles propaga-se para os coeficientes, escrevemos: | fonte de erro. Assim para ver como o erro neles propaga-se para os coeficientes, escrevemos: | ||
<math>a = a(y_i) \Rightarrow \frac{\partial a}{\partial y_i} = \frac{1}{\Delta} \frac{\partial }{\partial y_i} \left\{[ | <math>a = a(y_i) \Rightarrow \frac{\partial a}{\partial y_i} = \frac{1}{\Delta} \frac{\partial }{\partial y_i} \left\{[yw][x^2w] - [xyw][xw]\right\}</math> | ||
<math>\frac{\partial a}{\partial y_i} = \frac{1}{\Delta}\left\{ w_i[ | <math>\frac{\partial a}{\partial y_i} = \frac{1}{\Delta}\left\{ w_i[x^2w] - x_i w_i [xw]\right\}</math> | ||
Só os termos com y contribuem para a derivada. Como os <math>y_i</math> aparecem somados, ao derivar respeito do ''i''-esimo | |||
sobra apenas o que multiplica ele | sobra apenas o que multiplica ele | ||
Para incluir o efeito do erro de cada y_i deveriamos somar i de 1 a N, mas como o erro pode ser para mais o menos | Para incluir o efeito do erro de cada <math>y_i</math> deveriamos somar i de 1 a N, mas como o erro pode ser para mais o menos | ||
fazemos uma media quadrática deles: | fazemos uma media quadrática deles: | ||
| Linha 231: | Linha 231: | ||
onde: | onde: | ||
<math>\left(\frac{\partial a}{\partial y_i}\Delta y_i \right)^2 = \frac{1}{\Delta^2} \left\{ w_i^2[ | <math>\left(\frac{\partial a}{\partial y_i}\Delta y_i \right)^2 = \frac{1}{\Delta^2} \left\{ w_i^2[x^2w]^2 + x_i^2 w_i^2 [xw]^2 - 2w_i[x^2w] x_i w_i [xw]\right\}w_i^{-1}</math> | ||
o somatório fica: | o somatório fica: | ||
<math>\frac{1}{\Delta^2} \sum_{i=1}^N \left(w_i[ | <math>\frac{1}{\Delta^2} \sum_{i=1}^N \left(w_i[x^2w]^2 + x_i^2 w_i [xw]^2 - 2 [x^2w] x_i w_i [xw]\right) = | ||
\frac{1}{\Delta^2} \left([w][ | \frac{1}{\Delta^2} \left([w][x^2w]^2 + [x^2w][xw]^2 - 2 [x^2w][xw][xw]\right)</math> | ||
e com mais algumas simplificações chegamos a simples relação: | e com mais algumas simplificações chegamos a simples relação: | ||
<math>\Delta a = \sqrt{\frac{[ | <math>\Delta a = \sqrt{\frac{[x^2w]}{\Delta}}</math> | ||
Analogamente para o b (que resulta ser mais fácil), se chega a: | Analogamente para o b (que resulta ser mais fácil), se chega a: | ||
| Linha 252: | Linha 252: | ||
<math>w=1/(\Delta y)^2</math> | <math>w=1/(\Delta y)^2</math> | ||
:<math>\Rightarrow \Delta = w^2 (N[ | :<math>\Rightarrow \Delta = w^2 (N[x^2] - [x]^2)= (w N \sigma)^2</math> | ||
onde <math>\sigma^2 = <x^2> - <x>^2</math> | onde <math>\sigma^2 = <x^2> - <x>^2</math> | ||
| Linha 266: | Linha 266: | ||
* E erro das medidas (<math>\Delta y</math>) que deve ser minimizado, porem está geralmente limitado pelo instrumento utililizado | * E erro das medidas (<math>\Delta y</math>) que deve ser minimizado, porem está geralmente limitado pelo instrumento utililizado | ||
* O número de medidas <math>N</math>, quanto maior, melhor, porem vemos que o erro dos coeficientes diminui com a raiz dele | * O número de medidas <math>N</math>, quanto maior, melhor, porem vemos que o erro dos coeficientes diminui com a raiz dele | ||
* Por último, a dispersão da viariável | * Por último, a dispersão da viariável independente x (<math>\sigma</math>) também, quanto maior, melhor | ||
Por último, consideremos o caso mais simples, ajuste sem ponderar e sem informação sobre <math>\Delta y</math>, apenas <math>N</math> pares de dados {<math>{x_i, y_i}</math>}. | Por último, consideremos o caso mais simples, ajuste sem ponderar e sem informação sobre <math>\Delta y</math>, apenas <math>N</math> pares de dados {<math>{x_i, y_i}</math>}. | ||
Edição atual tal como às 11h22min de 27 de julho de 2021
Este o nome que se da ao ajuste ou fitting de uma função (polinômio) a um conjunto de dados.
Se com representam o conjunto de dados (N) obtidos de um experimento (instrumento) ou
de uma observação (por exemplo, em pesquisa de opinião ou censo) ou de uma simulação numérica.
E se suspeitamos que existe uma correlação entre os X (variável independente ou de entrada, controlada pelo experimento)
e os Y (cuja dependência com X queremos testar), primeiro colocamos os pontos num gráfico para ver se o conjunto forma
uma nuvem dispersa (quando não existe correlação aparente, isto é X e Y não conformam uma função), ou se existe
correlação (os pontos parecem estar sobre alguma curva).
Equação linear
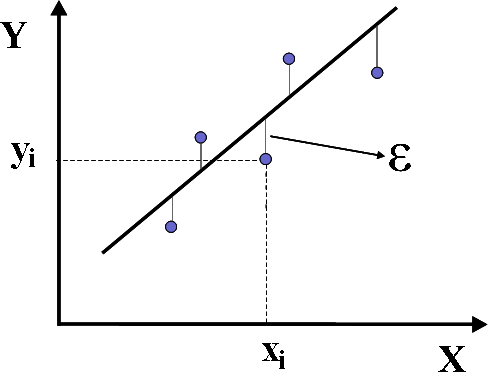
Sendo que um experimento foi realizado e temos pontos, como descrito acima, e consideramos que um ajuste linear é coerente, uma reta deve ser construída para melhor representar estes pontos. Como mostrado na figura a baixo, para cada ponto, teremos um erro , que é definido como a distância entre o ponto experimental e a curva (reta neste caso) teórica que desejamos ajustar, ou seja,
- ,
onde
é a função que representa a curva de melhor ajuste.
Para encontrar a reta que melhor se ajusta aos dados experimentais, desejamos minimizar o erro . Como o erro pode ter tanto valores negativos quanto positivos, o que importa é minimizar o valor absoluto de . Isto poderia ser feito minimizando módulo de , mas como a função módulo tem uma descontinuidade, é mais fácil minimizar o quadrado do erro. Para isto, definimos:
- ,
assim
- .
Para obter a melhor reta que se ajusta aos dados experimentais, temos que minimizar em relação às constantes da função :
- .
Como a reta possui apenas dois coeficientes, para o ajuste linear temos duas equações:
e
- .
Derivando as equações acima, temos que
e
- .
Assim,
e
- .
Lembre-se de que os valores e são conhecidos (são dados do problema). Desse modo, terminamos com um sistema linear para resolver, que na notação matricial fica
- .
Cuidado com o fato que e . Após construir a matriz, resolva com o método que mais lhe agrade (ha diversos métodos de solução de sistemas lineares, tais como a Regra de Cramer ou a eliminação Gaussiana).
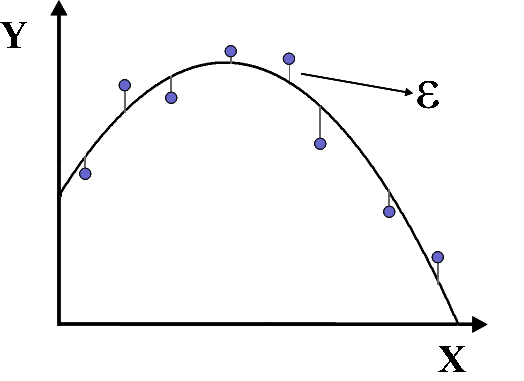
Equação quadrática
Utilizando o mesmo método descrito para um ajuste linear, considerando que o melhor ajuste para um conjunto de pontos seja uma curva proveniente de função quadrática, temos que a função é dada por
- .
Desse modo, a soma do quadrado do erro fica
- .
Após algumas contas, como feito na seção anterior, temos o sistema linear de 3 equações e 3 incógnitas para resolver:
- .
Fique atento ao fato de que
- .
Polinômio de grau n
Generalizando o procedimento acima, apresentado para polinômios de grau 1 e 2, podemos ajustar um conjunto de pontos com um polinômio de um grau específico . Assim, a função será descrita por
e a soma dos quadrados do erro é dada por
- .
Ao final do procedimento, teremos um sistema linear de equações e incógnitas para resolver. O resultado deste sistema são os coeficientes : que compõem o polinômio que melhor se ajusta aos dados experimentais.
Outros tipos de funções
Dependendo do tipo de experimento, podem haver outras relações entre os pontos, como funções exponenciais.
Exponencial 1
Se os dados de um experimento se ajustarem bem a uma função exponencial do tipo:
- ,
definimos uma nova função :
- .
Assim, recaímos no problema do ajuste linear recém visto:
- , com e .
Exponencial 2
Se a função exponencial for do tipo:
- ,
supondo , definimos:
- .
Assim, como no caso anterior, voltamos para o problema de ajuste linear:
- ,
com e .
Algébrica
Se a função for do tipo:
- ,
com e , definimos:
- .
e assim
- ,
onde e . Note também que os valores de x devem ser transformados em para ajustar os pontos.
Código FORTRAN
A seguir vemos uma possível implementação do método em linguagem F90.
Observem a simplicidade do mesmo:
! programa fortran para ajuste linear de conjunto de dados
Implicit none
Real :: xi,yi, x,y,xy,x2
Real :: det,a,b
n = 0; x = 0; y = 0; xy = 0; x2 = 0
Do
Read(*,*,end=100) xi,yi
n = n + 1 ! soma do numero de pontosd
x = x + xi; y = y + yi ! somatorio dos x e y
x2 = x2 + xi**2; xy = xy + xi*y ! somatorio dos x**2 e x*y <- cuidado ha um erro aqui (compila mas ...
End Do
100 det = n*x2 - x**2
a = y*x2 - xy*x / det ! <- outro erro aqui
b = ... / det ! fica como exercicio
print*, 'a=', a, 'b=', b
end
Ajuste ponderado
Dependendo da situação, convém fazer um ajuste levando em conta o erro associado a cada ponto, i.e., atribuindo maior peso para pontos com um erro baixo e menor peso para os pontos onde o erro é sabidamente maior. Ou seja, se definirmos como o peso associado ao ponto , gostaríamos que ele seja maior quanto menor for o erro associado a este ponto. Se é o erro associado a este ponto, e considerando que o ajuste proposto é tal que minimiza a distância quadrática, podemos definir então como:
E o resíduo , para o cálculo do ajuste ponderado, será dada por:
Aplicando o mesmo procedimento anterior para minimizar , obtemos as equações
E, portanto, os valores de e são:
com :
Erro dos coeficientes
Vimos como obter os coeficientes (a e b para uma reta) do ajuste de um conjunto de dados.
Também como fazer esse ajuste quando os erros na variável dependente y não são todos iguais.
Mas como saber se esses coeficientes são "bons". Ou seja, que margem de erro eles tem.
Intuitivamente sabemos que quanto maior seja a dispersão dos em volta
da curva do ajuste, maior será nossa incerteza sobre os coeficientes.
Vamos ver como traduzir isso de forma quantitativa. Voltando as expressões dos coeficientes a e b, eles são funções de e , onde só os segundos são considerados como fonte de erro. Assim para ver como o erro neles propaga-se para os coeficientes, escrevemos:
Só os termos com y contribuem para a derivada. Como os aparecem somados, ao derivar respeito do i-esimo sobra apenas o que multiplica ele
Para incluir o efeito do erro de cada deveriamos somar i de 1 a N, mas como o erro pode ser para mais o menos fazemos uma media quadrática deles:
onde:
o somatório fica:
e com mais algumas simplificações chegamos a simples relação:
Analogamente para o b (que resulta ser mais fácil), se chega a:
Podemos interpretar essa expressões no caso sem ponderar, ou seja quando todos os erros são iguais:
onde
resultando:
Por tanto, três fatores determinam a qualidade do ajuste:
- E erro das medidas () que deve ser minimizado, porem está geralmente limitado pelo instrumento utililizado
- O número de medidas , quanto maior, melhor, porem vemos que o erro dos coeficientes diminui com a raiz dele
- Por último, a dispersão da viariável independente x () também, quanto maior, melhor
Por último, consideremos o caso mais simples, ajuste sem ponderar e sem informação sobre , apenas pares de dados {}. Nesse caso podemos estimar o valor de pelo assim:
Pois o resíduo pode ser interpretado como o somatório dos erros de cada ponto, tomados como a distancia entre a medida e o ajuste. O em lugar de , é pelo fato de que o ajuste já contem dois parâmetros ( e obtidos dos dados, então os erros individuais não são todos independentes.








![{\displaystyle S=\sum _{i=1}^{N}[y_{i}-f(x_{i})]^{2}=\sum _{i=1}^{N}[y_{i}-f(x_{i};\alpha _{0},\alpha _{1})]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1245b058d6989407abd78201c87c153148fa83d)



![{\displaystyle {\frac {\partial S}{\partial \alpha _{0}}}={\frac {\partial }{\partial \alpha _{0}}}\sum _{i=1}^{N}[y_{i}-(\alpha _{0}+\alpha _{1}x_{i})]^{2}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/453107e85595c84d4a5a13b39af579b6aedf4da9)
![{\displaystyle {\frac {\partial S}{\partial \alpha _{1}}}={\frac {\partial }{\partial \alpha _{1}}}\sum _{i=1}^{N}[y_{i}-(\alpha _{0}+\alpha _{1}x_{i})]^{2}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e114fd860bec8e9aaa0e5c9f73d817e338cb1e9e)










![{\displaystyle S=\sum _{i=1}^{N}\epsilon _{i}^{2}=\sum _{i=1}^{N}[Y_{i}-(\alpha _{0}+\alpha _{1}X_{i}+\alpha _{2}X_{i}^{2})]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e02aef60d147a7470972e92366180c2e00d1358d)




![{\displaystyle S=\sum _{i=1}^{N}\epsilon _{i}^{2}=\sum _{i=1}^{N}[Y_{i}-f(X_{i};\alpha _{0},\alpha _{1},...,\alpha _{n})]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a0d65cee2817a4d962b85c81d8a40c178eb03f5)























![{\displaystyle {\begin{bmatrix}a[w]+b[xw]&=&[yw]\\a[xw]+b[x^{2}w]&=&[xyw]\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e642c191100dd64c2e4c26eace838a5839b016a8)


![{\displaystyle a=([yw][x^{2}w]-[xyw][xw])/\Delta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/863017a59ffb2027ade2b82f528d357be95ffea2)
![{\displaystyle b=([w][xyw]-[xw][yw])/\Delta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/94b63442ae2c04205232deaae39a1420254e592b)

![{\displaystyle \Delta =[w][x^{2}w]-[xw]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7b930326b63a48be11cc3db523f1ccca29ef715)
![{\displaystyle a=a(y_{i})\Rightarrow {\frac {\partial a}{\partial y_{i}}}={\frac {1}{\Delta }}{\frac {\partial }{\partial y_{i}}}\left\{[yw][x^{2}w]-[xyw][xw]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51b99add5917011f2d4ea64929ad645b7f2e7616)
![{\displaystyle {\frac {\partial a}{\partial y_{i}}}={\frac {1}{\Delta }}\left\{w_{i}[x^{2}w]-x_{i}w_{i}[xw]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab0a62807c7fe5a9bc51de45bb8ab696e85e3963)

![{\displaystyle \left({\frac {\partial a}{\partial y_{i}}}\Delta y_{i}\right)^{2}={\frac {1}{\Delta ^{2}}}\left\{w_{i}^{2}[x^{2}w]^{2}+x_{i}^{2}w_{i}^{2}[xw]^{2}-2w_{i}[x^{2}w]x_{i}w_{i}[xw]\right\}w_{i}^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0545ae90c649c5cf426294181069e7f21a549a13)
![{\displaystyle {\frac {1}{\Delta ^{2}}}\sum _{i=1}^{N}\left(w_{i}[x^{2}w]^{2}+x_{i}^{2}w_{i}[xw]^{2}-2[x^{2}w]x_{i}w_{i}[xw]\right)={\frac {1}{\Delta ^{2}}}\left([w][x^{2}w]^{2}+[x^{2}w][xw]^{2}-2[x^{2}w][xw][xw]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/100d027f491b7f46464f9126249987aa489b8de3)
![{\displaystyle \Delta a={\sqrt {\frac {[x^{2}w]}{\Delta }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f1db2967a05725ad2ad9bf74e8e6f14d3a2edd8)
![{\displaystyle \Delta b={\sqrt {\frac {[w]}{\Delta }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03aad5e8f06c46ad5345376b466216026aefdf31)

![{\displaystyle \Rightarrow \Delta =w^{2}(N[x^{2}]-[x]^{2})=(wN\sigma )^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ae9da2606653331e686c8a9bbdd5bbc8071eb19)







