Grupo - Modelo Sznajd: mudanças entre as edições
Sem resumo de edição |
|||
| (7 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 22: | Linha 22: | ||
# Se <math> S_{i} = -S_{i+1}</math>, então <math> S_{i-1} = S_{i}</math> e <math> S_{i+2} = S_{i}</math> | # Se <math> S_{i} = -S_{i+1}</math>, então <math> S_{i-1} = S_{i}</math> e <math> S_{i+2} = S_{i}</math> | ||
Estas regras ficaram conhecidas como algo do tipo: "Se você não sabe o que fazer, ou faz nada ou faz qualquer coisa." É um tanto quanto óbvio que o modelo unidimensional não representa bem um sistema social e que modelos bidimensionais são bem mais realistas. Algo interessante mencionar é a atualização simultânea para sistemas de duas dimensões: uma atualização simultânea leva a uma muito maior dificuldade de atingir o estado de consenso total. Isso foi mostrado por Stauffer<ref>D. Stauffer D, J Math Sociol 28 25 (2004)</ref> e a | Estas regras ficaram conhecidas como algo do tipo: "Se você não sabe o que fazer, ou faz nada ou faz qualquer coisa." É um tanto quanto óbvio que o modelo unidimensional não representa bem um sistema social e que modelos bidimensionais são bem mais realistas. Algo interessante mencionar é a atualização simultânea para sistemas de duas dimensões: uma atualização simultânea leva a uma muito maior dificuldade de atingir o estado de consenso total. Isso foi mostrado por Stauffer<ref>D. Stauffer D, J Math Sociol 28 25 (2004)</ref> e a razão para isso é que alguns recebem simultaneamente distintas informações de diferentes vizinhos, o que leva a não aceitar a opinião. | ||
Regras para rede quadrada <math> | Regras para rede quadrada <math>L</math>x<math>L</math>: | ||
# Se conjunto 2x2 de 4 vizinhos não tiverem todos os seus spins paralelos, deixam os seus oito vizinhos sem | # Se conjunto 2x2 de 4 vizinhos não tiverem todos os seus spins paralelos, deixam os seus oito vizinhos sem .# Um par de vizinhos convence seus seis vizinhos a seguirem a sua orientação se o par de spins for paralelo. | ||
# Um par de vizinhos convence seus seis vizinhos a seguirem a sua orientação se o par de spins for paralelo. | |||
A regra de atualização para duas dimensões pode ser obtida pela regra em uma dimensão: A regra e 1D é aplicada para cada uma das 4 cadeias de spins, como mostra a próxima figura: | A regra de atualização para duas dimensões pode ser obtida pela regra em uma dimensão: A regra e 1D é aplicada para cada uma das 4 cadeias de spins, como mostra a próxima figura: | ||
[[Arquivo:1.jpg]] | [[Arquivo:1.jpg]] | ||
Isto foi mostrado por | Isto foi mostrado por Galam<ref>S. Galam, J. Stat. Phys. 61, 943 (1990)</ref> | ||
== Generalização == | == Generalização == | ||
| Linha 43: | Linha 42: | ||
<math>II.</math> Um par vizinho tenta convencer seus seis vizinhos a seguir a orientação do par apenas se o par tiver spins paralelos. Caso contrário, seguem três regras horizontais mas com regras verticais completamente análogas: | <math>II.</math> Um par vizinho tenta convencer seus seis vizinhos a seguir a orientação do par apenas se o par tiver spins paralelos. Caso contrário, seguem três regras horizontais mas com regras verticais completamente análogas: | ||
#<math>II_a</math> Os vizinhos não mudam | #<math>II_a</math> Os vizinhos não mudam. | ||
#<math>II_b</math> Os três vizinhos da esquerda seguem a orientação do spin da esquerda do par e os três da direita seguem o spin da direita | #<math>II_b</math> Os três vizinhos da esquerda seguem a orientação do spin da esquerda do par e os três da direita seguem o spin da direita. | ||
#<math>II_c</math> Os três vizinhos da esquerda seguem a orientação do spin da direita do par e os três da direita seguem o spin da esquerda (oposto a anterior) | #<math>II_c</math> Os três vizinhos da esquerda seguem a orientação do spin da direita do par e os três da direita seguem o spin da esquerda (oposto a anterior). | ||
<math>III.</math> A regra de 1D é aplicada para cada uma das quatro linhas de quatro spins cada. | <math>III.</math> A regra de 1D é aplicada para cada uma das quatro linhas de quatro spins cada. | ||
Regra <math>I_a:</math> pontos fixos com spins todos para cima ou para baixo | Regra <math>I_a:</math> pontos fixos com spins todos para cima ou para baixo. | ||
Regra <math>I_b:</math> sem pontos fixos | Regra <math>I_b:</math> sem pontos fixos. | ||
Regra <math>II_a</math> e <math>II_b:</math> pontos fixos com spins todos para cima ou para baixo | Regra <math>II_a</math> e <math>II_b:</math> pontos fixos com spins todos para cima ou para baixo. | ||
Regra <math>II_c:</math> Para L par ten-se ou tudo para cima ou para baixo. Para L ímpar também a o ponto antiferromagnético | Regra <math>II_c:</math> Para L par ten-se ou tudo para cima ou para baixo. Para L ímpar também a o ponto antiferromagnético | ||
Regra <math>III:</math> pontos fixos com spins todos para cima ou para baixo com L ímpar | Regra <math>III:</math> pontos fixos com spins todos para cima ou para baixo com L ímpar. | ||
== Aplicações == | == Aplicações == | ||
O modelo de Sznajd pode ser utilizado em política, marketing e finanças. Um caso especial está em <ref>A. T. BERNARDES et al, Int. J. Mod. Phys. C 12, 159 (2001)</ref> | O modelo de Sznajd pode ser utilizado em política, marketing e finanças. Um caso especial está em <ref>A. T. BERNARDES et al, Int. J. Mod. Phys. C 12, 159 (2001)</ref>. | ||
Reproduzimos o modelo mostrado no paper, usando uma rede quadrada <math> | Reproduzimos o modelo mostrado no paper, usando uma rede quadrada <math>N</math>x<math>N</math> com <math>N = 1000</math>. Ao invés de usar um modelo de spin (-1 ou 1), o modelo simula eleições brasileiras, usando um número de políticos escolhido como <math>N_p = 600</math>. Usando a condição de seleção <math>II_a</math>, cada vez que dois vizinhos tem a mesma opinião, todos os seus 6 vizinhos adquirem a mesma opinião. | ||
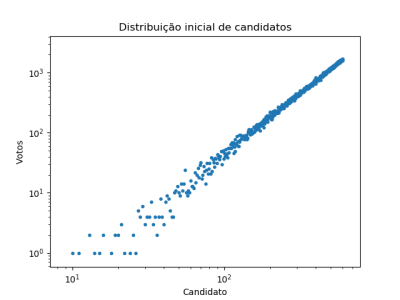
Nossa condição inicial é montada selecionando todos os eleitores aleatoriamente, dando-os uma probabilidade <math>P = \frac{n^2}{N^2}</math> de escolher um candidato <math>n</math>. Ao escolher um candidado, ele tem uma mesma probabilidade <math>P</math> de tentar convencer seus vizinhos (<math>P</math> nesse caso age como o poder de convencimento de um candidato). Na imagem podemos ver | Nossa condição inicial é montada selecionando todos os eleitores aleatoriamente, dando-os uma probabilidade <math>P = \frac{n^2}{N^2}</math> de escolher um candidato <math>n</math>. Ao escolher um candidado, ele tem uma mesma probabilidade <math>P</math> de tentar convencer seus vizinhos (<math>P</math> nesse caso age como o poder de convencimento de um candidato). Na imagem podemos ver a distribuição de votos por politico, que segue uma lei de potências. | ||
[[Arquivo:init.png|x300px]] | |||
Em seguida, realizamos passos de Monte Carlo, selecionando aleatóriamente <math>N^2</math> eleitores (que podem se repetir) e os fazemos tentar convencer um de seus 4 vizinhos, seguindo a mesma regra. | Em seguida, realizamos passos de Monte Carlo, selecionando aleatóriamente <math>N^2</math> eleitores (que podem se repetir) e os fazemos tentar convencer um de seus 4 vizinhos, seguindo a mesma regra. | ||
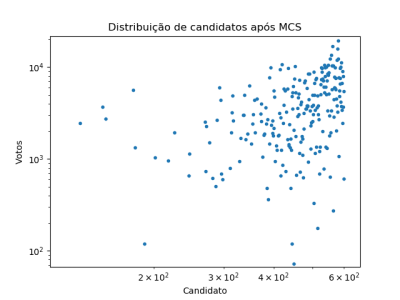
Nosso modelo tenta estudar a fase de transição do modelo (passos de Monte Carlo <math>1 << t << 10^5</math>), dado que num processo eleitoral os votos não atingem um equilíbrio. A imagem mostra a distribuição desses votos [ | Nosso modelo tenta estudar a fase de transição do modelo (passos de Monte Carlo <math>1 << t << 10^5</math>), dado que num processo eleitoral os votos não atingem um equilíbrio. A imagem mostra a distribuição desses votos. | ||
[[Arquivo:anferparty.png|x300px]] | |||
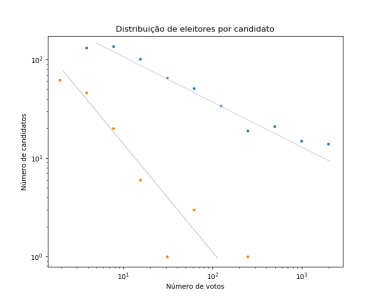
Após essa distribuição, podemos estudar como se dividem os votos. A imagem mostra a distribuição acumulada dos votos, em azul logo após a distribuição inicial (lei de potência com inclinação -1/2), e após os passos de Monte Carlo (com inclinação -1). Vemos que muitos poucos candidatos recebem a maioria dos votos, fato que concorda com o caso real.<ref>R. N. Costa-Filho, M. P. Almeida, J. S. Andrade Jr., and J. E. Moreira, Phys. Rev. E 60, 1067 (1999)</ref> | |||
[[Arquivo:final.png|x300px]] | |||
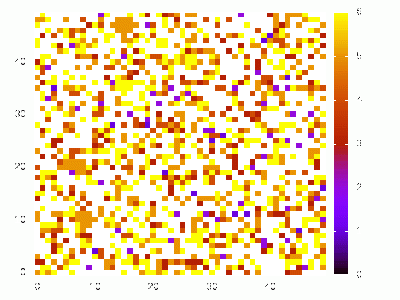
Uma maneira de visualizar o processo é vendo o que acontece em uma rede quadrada 50x50 com 6 candidatos. O sistema converge para um candidato dominando devido ao tamanho da rede. Para uma rede maior, há uma competição entre vários candidatos dentro do limite de transição. | |||
[[Arquivo:foobar.gif|x300px]] | |||
==Bibliografia== | ==Bibliografia== | ||
<references/> | <references/> | ||
Edição atual tal como às 07h42min de 25 de janeiro de 2018
Introdução
O Modelo de Sznajd ou United we stand, divided we fall (USDF) é um modelo recente, proposto em 2000 para entender a dinâmica de opiniões através da física estatística. No ponto de vista de um físico, o comportamento de indivíduos a as interações entre eles constituem um nível microscópico de um sistema social. O modelo introduz o fenômeno chamado validação social:
Validação Social: Se duas pessoas compartilham da mesma opinião, os seus vizinhos começarão a concordar com elas.
Discordância Destrutiva: Se as pessoas discordam, os vizinhos começarão a argumentar com elas.
O método e Formulação Matemática
Opinião social é vinda de opiniões individuais, representadas neste modelo por spins de Ising de forma "yes" e "no". A dinâmica segue a relação da validação social:
- A cada timestep um par de sping são escolhidos para tentar mudar os seus vizinhos mais próximos
- Se , então e (validação social)
- Se , então e
No modelo, dois tipos de estados estacionários são alcançáveis: consenso completo(ferromagnético) e impasse(antiferromagnético). A principal diferença para o Ising é que a informação flui para fora. O modelo de Sznajd ou USDF tem sido modificado e utilizado em marketing, política e finanças.
Modificações
Fala-se que o estado antes mencionado, o antiferromagnetismo, pode ser considerado não realístico para representar o comportamento de indivíduos em uma sociedade. Para tentar evitar este caso, propõe-se o seguinte:
- A cada timestep um par de sping são escolhidos para tentar mudar os seus vizinhos mais próximos igual anteriomente
- Se , então e (validação social)
- Se , então e
Estas regras ficaram conhecidas como algo do tipo: "Se você não sabe o que fazer, ou faz nada ou faz qualquer coisa." É um tanto quanto óbvio que o modelo unidimensional não representa bem um sistema social e que modelos bidimensionais são bem mais realistas. Algo interessante mencionar é a atualização simultânea para sistemas de duas dimensões: uma atualização simultânea leva a uma muito maior dificuldade de atingir o estado de consenso total. Isso foi mostrado por Stauffer[1] e a razão para isso é que alguns recebem simultaneamente distintas informações de diferentes vizinhos, o que leva a não aceitar a opinião.
Regras para rede quadrada x:
- Se conjunto 2x2 de 4 vizinhos não tiverem todos os seus spins paralelos, deixam os seus oito vizinhos sem .# Um par de vizinhos convence seus seis vizinhos a seguirem a sua orientação se o par de spins for paralelo.
A regra de atualização para duas dimensões pode ser obtida pela regra em uma dimensão: A regra e 1D é aplicada para cada uma das 4 cadeias de spins, como mostra a próxima figura:
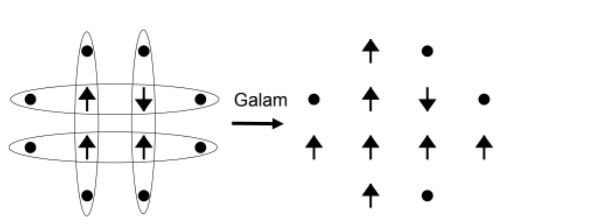
Isto foi mostrado por Galam[2]
Generalização
Para a generalização desse método para a rede quadrada x onde cada spin pode estar para cima ou para baixo e utiliza-se condições periódicas de contorno. As regras [3] esquematizadas:
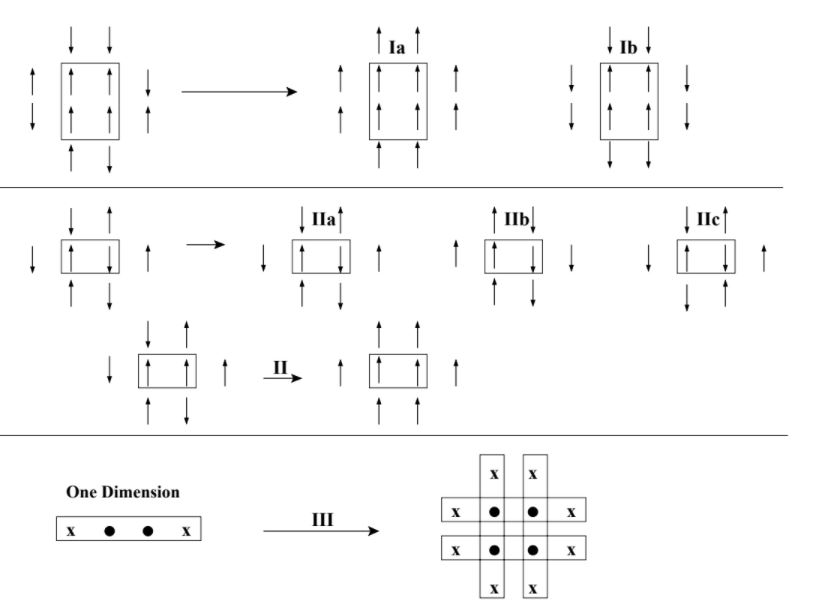
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle I.} Um conjunto 2x2 de quatro vizinhos é escolhido e se todos não forem paralelos, deixa os seus oito vizinhos sem mudanças. Se não, seguem duas regras:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_a} Os vizinhos seguem a orientação do conjunto.
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_b} Os vizinhos seguem a orientação oposta ao conjunto.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle II.} Um par vizinho tenta convencer seus seis vizinhos a seguir a orientação do par apenas se o par tiver spins paralelos. Caso contrário, seguem três regras horizontais mas com regras verticais completamente análogas:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle II_a} Os vizinhos não mudam.
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle II_b} Os três vizinhos da esquerda seguem a orientação do spin da esquerda do par e os três da direita seguem o spin da direita.
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle II_c} Os três vizinhos da esquerda seguem a orientação do spin da direita do par e os três da direita seguem o spin da esquerda (oposto a anterior).
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle III.} A regra de 1D é aplicada para cada uma das quatro linhas de quatro spins cada.
Regra Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_a:} pontos fixos com spins todos para cima ou para baixo.
Regra Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_b:} sem pontos fixos.
Regra Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle II_a} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle II_b:} pontos fixos com spins todos para cima ou para baixo.
Regra Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle II_c:} Para L par ten-se ou tudo para cima ou para baixo. Para L ímpar também a o ponto antiferromagnético
Regra Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle III:} pontos fixos com spins todos para cima ou para baixo com L ímpar.
Aplicações
O modelo de Sznajd pode ser utilizado em política, marketing e finanças. Um caso especial está em [4].
Reproduzimos o modelo mostrado no paper, usando uma rede quadrada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} xFalhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = 1000} . Ao invés de usar um modelo de spin (-1 ou 1), o modelo simula eleições brasileiras, usando um número de políticos escolhido como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_p = 600} . Usando a condição de seleção Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle II_a} , cada vez que dois vizinhos tem a mesma opinião, todos os seus 6 vizinhos adquirem a mesma opinião.
Nossa condição inicial é montada selecionando todos os eleitores aleatoriamente, dando-os uma probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \frac{n^2}{N^2}} de escolher um candidato Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} . Ao escolher um candidado, ele tem uma mesma probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} de tentar convencer seus vizinhos (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} nesse caso age como o poder de convencimento de um candidato). Na imagem podemos ver a distribuição de votos por politico, que segue uma lei de potências.
Em seguida, realizamos passos de Monte Carlo, selecionando aleatóriamente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N^2} eleitores (que podem se repetir) e os fazemos tentar convencer um de seus 4 vizinhos, seguindo a mesma regra.
Nosso modelo tenta estudar a fase de transição do modelo (passos de Monte Carlo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 << t << 10^5} ), dado que num processo eleitoral os votos não atingem um equilíbrio. A imagem mostra a distribuição desses votos.
Após essa distribuição, podemos estudar como se dividem os votos. A imagem mostra a distribuição acumulada dos votos, em azul logo após a distribuição inicial (lei de potência com inclinação -1/2), e após os passos de Monte Carlo (com inclinação -1). Vemos que muitos poucos candidatos recebem a maioria dos votos, fato que concorda com o caso real.[5]
Uma maneira de visualizar o processo é vendo o que acontece em uma rede quadrada 50x50 com 6 candidatos. O sistema converge para um candidato dominando devido ao tamanho da rede. Para uma rede maior, há uma competição entre vários candidatos dentro do limite de transição.
Bibliografia
- ↑ D. Stauffer D, J Math Sociol 28 25 (2004)
- ↑ S. Galam, J. Stat. Phys. 61, 943 (1990)
- ↑ D. Stauffer,A.O. Sousa,M. De Oliveira, Int. J. Mod. Phys. C 11 1239
- ↑ A. T. BERNARDES et al, Int. J. Mod. Phys. C 12, 159 (2001)
- ↑ R. N. Costa-Filho, M. P. Almeida, J. S. Andrade Jr., and J. E. Moreira, Phys. Rev. E 60, 1067 (1999)