Grupo - Conservação do Parâmetro de Ordem: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| Linha 65: | Linha 65: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>H = -\frac{1}{4}\epsilon\sum_{<ij>}s_is_j-\frac{1}{4}\epsilon\sum_{<ij>}s_i-\frac{1}{4}\epsilon\sum_{<ij>}s_j-\frac{1}{4}\epsilon\sum_{<ij>}1</math> </div> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>H = -\frac{1}{4}\epsilon\sum_{<ij>}s_is_j-\frac{1}{4}\epsilon\sum_{<ij>}s_i-\frac{1}{4}\epsilon\sum_{<ij>}s_j-\frac{1}{4}\epsilon\sum_{<ij>}1</math> </div> | ||
Seja <math>z</math> o número de coordenação da rede, ou seja, o número de primeiros vizinhos (<math>z=4</math> para rede quadrada e <math>z=6</math> para rede cúbica simples). Para uma dada rede existem <math | Seja <math>z</math> o número de coordenação da rede, ou seja, o número de primeiros vizinhos (<math>z=4</math> para rede quadrada e <math>z=6</math> para rede cúbica simples). Para uma dada rede existem <math\frac{1}{2}z N</math> possíveis pares distintos de primeiros vizinhos | ||
Pode-se simplificar esssa expressão com base nas seguintes observações: | Pode-se simplificar esssa expressão com base nas seguintes observações: | ||
| Linha 107: | Linha 107: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>M = \sum_i s_i = N(2\rho - 1)</math></div> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>M = \sum_i s_i = N(2\rho - 1)</math></div> | ||
No entanto, <math>\rho</math> e <math>N</math> devem permanecer constantes durante toda a simução, isso implica que a magnetização também é sempre constante, ou seja, a | No entanto, <math>\rho</math> e <math>N</math> devem permanecer constantes durante toda a simução, isso implica que a magnetização também é sempre constante, ou seja, a magnetização é o '''parâmetro de ordem conservado''' nesse sistema fato que dá nome ao método. | ||
É vantajoso tratar o modelo de gás de rede sob a perspectiva de um modelo de Ising pois todo o arcabouço de técnicas amplamente conhecidas e extensivamente estudadas para o modelo de Ising podem ser aplicadas. | É vantajoso tratar o modelo de gás de rede sob a perspectiva de um modelo de Ising pois todo o arcabouço de técnicas amplamente conhecidas e extensivamente estudadas para o modelo de Ising podem ser aplicadas. | ||
Apesar das similaridades, o gás de rede, como definido, possui muito menos estados válidos pois não é permitido alterar a magnetização do sistema enquanto no modelo de Ising qualquer spin individual pode ser invertido sem restrições pois a magnetização não precisa se manter constante. | Apesar das similaridades, o gás de rede, como definido, possui muito menos estados válidos (<math>\frac{1}{2}z N</math>) pois não é permitido alterar a magnetização do sistema enquanto no modelo de Ising qualquer spin individual pode ser invertido sem restrições pois a magnetização não precisa se manter constante (<math>2^N</math> estados possíveis). | ||
==Transição de fase== | ==Transição de fase== | ||
Aproveitando a equivalência estabelecida entre gás de rede e o modelo de Ising sabe-se que o sistema possui uma transição de fase que ocorre a uma temperatura crítica <math>T_c</math>. Rearranjando a densidade de pontos (equivalente agora | Aproveitando a equivalência estabelecida entre gás de rede e o modelo de Ising sabe-se que o sistema possui uma transição de fase que ocorre a uma temperatura crítica <math>T_c</math>. Rearranjando a densidade de pontos (equivalente agora à densidade de spins up) tem-se: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>2\rho - 1 = \frac{M}{N}</math></div> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>2\rho - 1 = \frac{M}{N}</math></div> | ||
| Linha 130: | Linha 130: | ||
* E outra em que <math>\rho\not\in[\rho_-,\rho_+]</math> tendo densidade homogênea | * E outra em que <math>\rho\not\in[\rho_-,\rho_+]</math> tendo densidade homogênea | ||
Com <math>\rho</math> sujeito ao intervalo <math>\frac{1}{2}(1-|m|) \le \rho \le \frac{1}{2}(1+|m|)</math> conclui-se que <math> | |||
Com <math>\rho</math> sujeito ao intervalo <math>\frac{1}{2}(1-|m|) \le \rho \le \frac{1}{2}(1+|m|)</math> conclui-se que <math>\rho</math> pode assumir um intervalo menor de valores a medida que <math>|m|</math> diminui. A magnetização diminui sob o aumento da temperatura. Acima da temperatura crítica a <math>|m|=0</math> e portanto o intervalo <math>\frac{1}{2}(1-|m|) \le \rho \le \frac{1}{2}(1+|m|)</math> reduz-se a zero evidenciando que não existe mais um valor de <math>\rho</math> que evite a homogeinização da rede. | |||
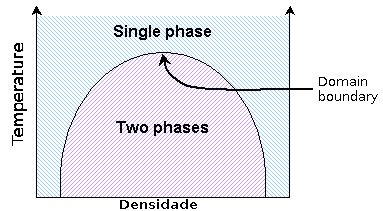
A discussão acima pode ser apresentada resumidamente pelo diagrama de fases: | A discussão acima pode ser apresentada resumidamente pelo diagrama de fases: | ||
| Linha 138: | Linha 139: | ||
Esse comportamento é observado quando se diminui a temperatura de vapor d'agua que passa a formar gotas líquidas que coexistem com o vapor para um intervalo de temperaturas. A fase condensada do gás de rede, no entanto, é mais adequadamente interpretada como um sólido devido a posição fixa das partículas (análogas a moléculas ou átomos) na rede, dessa forma, falamos de interface vapor/sólido ao invés de vapor/líquido. | Esse comportamento é observado quando se diminui a temperatura de vapor d'agua que passa a formar gotas líquidas que coexistem com o vapor para um intervalo de temperaturas. A fase condensada do gás de rede, no entanto, é mais adequadamente interpretada como um sólido devido a posição fixa das partículas (análogas a moléculas ou átomos) na rede, dessa forma, falamos de interface vapor/sólido ao invés de vapor/líquido. | ||
== | ==Teoria<ref name=newman>Newman, M. E. J.; Barkema, G. T. (1999). "Monte Carlo Methods in Statistical Physics" New York: Oxford University Press. ISBN 019-851796-3.</ref><ref name=krauth>Krauth, Werner (2006). "Statiscal Mechanics: Algorithms and Computations" New York: Oxford University Press. ISBN 978-0-19-851535-7.</ref>== | ||
Sistemas físicos em equilíbrio com muitos graus de liberdade e no limite termodinâmico comportam-se de tal forma que ao flutuarem de um estado <math>\mu</math> para um estado <math>\nu</math> tem-se que <math>\nu</math> difere pouco de <math>\mu</math>. Outra maneira de dizer isso é que as flutuações dessa tipo de sistema físico são muito pequenas em relação ao número de configurações possíveis e que portanto o sistema passa a maior parte do tempo alternando entre um pequeno conjunto de configurações. A consequência disso é que pode-se escolher uma estratégia de visitar com maior probabilidade apenas a fração de estados do sistema, as quais mais contribuem para atingir o equilíbrio ao invés de se visitar todos os estados indistintamente. No modelo de ferromagneto, por exemplo, com uma rede <math>10\times 10\times 10</math>, há <math>2^{1000} \simeq 10^{300}</math> configurações possíveis sendo que mesmo com um supercomputador seria impraticável realizar essa simulação. O método de Monte Carlo consiste em visitar eficientemente uma pequena fração desses estados e atingir rapidamente o equilíbrio em poucos passos e o peso que define como visitar o estado seguinte é dado pela distribuição de Boltzmann <math>e^{\beta(E_\nu-E_\mu)}</math> onde fica claro que quanto mais diferente <math>\nu</math> for de <math>\mu</math> menor a change de fazer a transição <math>\mu\to\mu</math> | Sistemas físicos em equilíbrio com muitos graus de liberdade e no limite termodinâmico comportam-se de tal forma que ao flutuarem de um estado <math>\mu</math> para um estado <math>\nu</math> tem-se que <math>\nu</math> difere pouco de <math>\mu</math>. Outra maneira de dizer isso é que as flutuações dessa tipo de sistema físico são muito pequenas em relação ao número de configurações possíveis e que portanto o sistema passa a maior parte do tempo alternando entre um pequeno conjunto de configurações. A consequência disso é que pode-se escolher uma estratégia de visitar com maior probabilidade apenas a fração de estados do sistema, as quais mais contribuem para atingir o equilíbrio ao invés de se visitar todos os estados indistintamente. No modelo de ferromagneto, por exemplo, com uma rede <math>10\times 10\times 10</math>, há <math>2^{1000} \simeq 10^{300}</math> configurações possíveis sendo que mesmo com um supercomputador seria impraticável realizar essa simulação. O método de Monte Carlo consiste em visitar eficientemente uma pequena fração desses estados e atingir rapidamente o equilíbrio em poucos passos e o peso que define como visitar o estado seguinte é dado pela distribuição de Boltzmann <math>e^{\beta(E_\nu-E_\mu)}</math> onde fica claro que quanto mais diferente <math>\nu</math> for de <math>\mu</math> menor a change de fazer a transição <math>\mu\to\mu</math> | ||
| Linha 150: | Linha 151: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>A(\mu\to\nu)=A_0e^{-\frac{1}{2}\beta(E_\nu-E_\mu)}</math></div> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>A(\mu\to\nu)=A_0e^{-\frac{1}{2}\beta(E_\nu-E_\mu)}</math></div> | ||
Tomando <math>g(\mu) = g(\nu)</math> e como <math>A_0</math> é cancelada na razão entre probabilidades de aceitação temos a liberdade na sua escolha desde que mantenha a probabilidade menor ou igual a um. No modelo de ferromagneto, por exemplo, a maior diferença de energia que se pode obter entre estados é <math>\Delta E = E_\nu-E_\mu = \pm 2zJ</math> o que significa que o maior valor de <math>e^{-\frac{1}{2}\beta(E_\nu-E_\mu)}</math> é justamente <math>e^{\beta zJ}</math>. Assim, para garantir que a probabilidade seja menor ou igual a 1 deve-se escolher <math>A_0 \le e^{-\beta zJ}</math> | |||
Para que o algoritmo seja eficiente deseja-se que a probabilidade de aceitação seja a maior possível, pois do contrário estaríamos utilizando tempo computacional apenas para rejeitar trocas de estado. Portanto queremos que <math>A_0</math> assuma o maior valor possível <math>A_0 = e^{-\beta zJ}</math>, maximizando <math>A(\mu\to\nu)</math>: | Para que o algoritmo seja eficiente deseja-se que a probabilidade de aceitação seja a maior possível, pois do contrário estaríamos utilizando tempo computacional apenas para rejeitar trocas de estado. Portanto queremos que <math>A_0</math> assuma o maior valor possível <math>A_0 = e^{-\beta zJ}</math>, maximizando <math>A(\mu\to\nu)</math>: | ||
| Linha 168: | Linha 169: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>A(\mu\to\nu)=e^{-\beta(E_\nu-E_\mu)}</math></div> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>A(\mu\to\nu)=e^{-\beta(E_\nu-E_\mu)}</math></div> | ||
Dessa forma a transição de estados sempre ocorre se <math>E_\nu < E_\mu</math> ou seja <math>\Delta E < | Dessa forma a transição de estados sempre ocorre se <math>E_\nu < E_\mu</math> ou seja <math>\Delta E < 0</math> mas pode ou não ocorrer caso seja <math>\Delta E > 0</math> com uma probabilidade dada por <math>e^{-\beta(E_\nu-E_\mu)}</math>. Em suma: | ||
<math> | <math> | ||
| Linha 177: | Linha 178: | ||
</math> | </math> | ||
== | ==Implementação<ref name=newman/>== | ||
Para obedecer a condição de conservação da magnetização não é permitido alterar um spin individualmente (ou um número ímpar de spins). Uma maneira de tratar a dinâmica desse sistema foi proposta por Kawasaki <ref name=kawasaki>[https://link.aps.org/doi/10.1103/PhysRevLett.49.1223 T. Ohta, D. Jasnow and K. Kawasaki, Phys. Rev. Lett. 49 1223 (1982). "Universal Scaling in the Motion of Random Interfaces". American Physical Society]</ref> e consiste em simplesmente alternar o estado de spin de um par de | Para obedecer a condição de conservação da magnetização não é permitido alterar um spin individualmente (ou um número ímpar de spins). Uma maneira de tratar a dinâmica desse sistema foi proposta por Kawasaki <ref name=kawasaki>[https://link.aps.org/doi/10.1103/PhysRevLett.49.1223 T. Ohta, D. Jasnow and K. Kawasaki, Phys. Rev. Lett. 49 1223 (1982). "Universal Scaling in the Motion of Random Interfaces". American Physical Society]</ref> e consiste em simplesmente alternar o estado de spin de um par de | ||
| Linha 192: | Linha 191: | ||
</math> | </math> | ||
É evidente que nesse caso a mudança | É evidente que nesse caso a mudança conserva a magnetização, pois a troca de spins resulta em variação de magnetização nula. | ||
Cada ponto da rede possui <math>z</math> vizinhos e portanto a cada passo de iteração deve-se sortear com qual dos vizinhos será feita uma tentativa de troca de spins. Essa escolha é feita aleatoriamente (uniforme). Uma vez escolhido um vizinho deve-se decidir se a troca deve ser feita ou não. Essa decisão é tomada com base no método de Monte Carlo, em particular, com a probabilidade de aceitação de Metropolis exatamente como exposto na seção acima. | Cada ponto da rede possui <math>z</math> vizinhos e portanto a cada passo de iteração deve-se sortear com qual dos vizinhos será feita uma tentativa de troca de spins. Essa escolha é feita aleatoriamente (uniforme). Uma vez escolhido um vizinho deve-se decidir se a troca deve ser feita ou não. Essa decisão é tomada com base no método de Monte Carlo, em particular, com a probabilidade de aceitação de Metropolis exatamente como exposto na seção acima. | ||
| Linha 209: | Linha 208: | ||
Seja um ponto da rede <math>k</math> e <math>k'</math> primeiro vizinho de <math>k</math>. Deseja-se calcular a energia de interação entre esse par. A expressão acima apenas diz que deve-somar os produtos do spin de <math>k</math>, <math>(s_k)</math>, com seus primeiros vizinhos <math>s_i</math> excluindo-se da soma tanto <math>k</math> quanto <math>k'</math>. Faz-se o mesmo procedimento para <math>k'</math>, ou seja, soma-se os produtos do spin <math>k'</math>, <math>(s_{k'})</math>, com todos os seus primeiros vizinhos <math>s_j</math> exceto ele mesmo e <math>k</math>. A soma dessas duas quantidades multiplicadas por <math>2J</math> é igual a diferença de energia entre a configuração <math>\mu</math> e a <math>\nu</math> | Seja um ponto da rede <math>k</math> e <math>k'</math> primeiro vizinho de <math>k</math>. Deseja-se calcular a energia de interação entre esse par. A expressão acima apenas diz que deve-somar os produtos do spin de <math>k</math>, <math>(s_k)</math>, com seus primeiros vizinhos <math>s_i</math> excluindo-se da soma tanto <math>k</math> quanto <math>k'</math>. Faz-se o mesmo procedimento para <math>k'</math>, ou seja, soma-se os produtos do spin <math>k'</math>, <math>(s_{k'})</math>, com todos os seus primeiros vizinhos <math>s_j</math> exceto ele mesmo e <math>k</math>. A soma dessas duas quantidades multiplicadas por <math>2J</math> é igual a diferença de energia entre a configuração <math>\mu</math> e a <math>\nu</math> | ||
A simulação é extremamente simplificada pelo fato de o estado final não figurar na expressão para o cálculo da diferença de energia da transição, pois pode-se verificar de antemão se a transição deve ser feita sem que seja necessário efetivamente colocar o sistema no estado final <math>\nu</math>. | |||
==Simulação== | ==Simulação== | ||
Foram simulados três sistemas diferentes os quais são discutidos a seguir. O objetivo das simulações em determinar a tendência do formato de cada interface após vários passos de monte carlo sem verificar rigorosamente se o equilíbrio foi atingido. Uma análise das condições de equilíbrio é discutida na última seção. | Foram simulados três sistemas diferentes os quais são discutidos a seguir. O objetivo das simulações em determinar a tendência do formato de cada interface após vários passos de monte carlo sem verificar rigorosamente se o equilíbrio foi atingido. Uma análise das condições de equilíbrio é discutida na última seção. | ||
Todas as simulações demandam a geração de muitos números aleatórios por isso optou-se por usar Mersenne Twister | Todas as simulações demandam a geração de muitos números aleatórios por isso optou-se por usar Mersenne Twister - um algoritmo veloz para geração de números aleatórios. | ||
===Interface linear=== | ===Interface linear=== | ||
Esse sistema consiste rede quadrada de aresta <math>l</math>. A rede tem inicialmente sua metade inferior completamente populada por partículas. | Esse sistema consiste de uma rede quadrada de aresta <math>l</math>. A rede tem inicialmente sua metade inferior completamente populada por partículas (spins up) e o restante da rede possui vacâncias (spins down). | ||
Cada ponto da rede é visitado sequencialmente e um dos seus 4 vizinhos é sorteado para que se faça uma tentativa de troca de posição entre o par. Caso a energia do sistema diminua, a troca é feita com probabilidade 1. Caso contrário a troca ocorre com probabilidade dada pelo peso de Boltzmann (algoritmo de Metropolis). | Cada ponto da rede é visitado sequencialmente e um dos seus 4 vizinhos é sorteado para que se faça uma tentativa de troca de posição entre o par. Caso a energia do sistema diminua, a troca é feita com probabilidade 1. Caso contrário a troca ocorre com probabilidade dada pelo peso de Boltzmann (algoritmo de Metropolis). | ||
| Linha 226: | Linha 227: | ||
Ao iterar pela rede é comum deparar-se com pares de vizinhos que possuem mesma orientação de spin e portanto são ignorados imediatamente pois em nada contribuem para a dinâmica do sistema. | Ao iterar pela rede é comum deparar-se com pares de vizinhos que possuem mesma orientação de spin e portanto são ignorados imediatamente pois em nada contribuem para a dinâmica do sistema. | ||
[[Arquivo:cop500iterinstepsof10.gif|frame|center|Interface linear entre sólido e vapor. Cada frame corresponde a 10 passos de Monte Carlo de um total de 500 passos. Primeira simulação com alta temperatura <math>T > T_C</math>. Segunda | [[Arquivo:cop500iterinstepsof10.gif|frame|center|Interface linear entre sólido e vapor. Cada frame corresponde a 10 passos de Monte Carlo de um total de 500 passos. Primeira simulação com alta temperatura <math>T > T_C</math>. Segunda simulação com temperatura intermediária <math>T < T_C</math>. Terceira simulação com baixa temperatura <math>T \ll T_C</math>]] | ||
Como observado, a alta temperatura recai-se no regime homogêneo em que a alternativa mais | Como observado, a alta temperatura recai-se no regime homogêneo em que a alternativa mais adequada para que o sistema minize sua energia é distribuir os spins up (partículas) uniformemente pela rede. | ||
A uma temperatura abaixo da crítica percebe-se a formação de uma interface persistente entre a região inferior com densidade preferencial <math>\rho_+</math> e a superior com densidade preferencial <math>\rho_-</math> em coexistência. | A uma temperatura abaixo da crítica percebe-se a formação de uma interface persistente entre a região inferior com densidade preferencial <math>\rho_+</math> e a superior com densidade preferencial <math>\rho_-</math> em coexistência. | ||
Ao diminuir ainda mais a temperatura o efeito fica mais acentuado, ou seja, a interface é menos deformada em relação ao caso anterior. | Ao diminuir ainda mais a temperatura o efeito fica mais acentuado, ou seja, a interface é menos deformada em relação ao caso anterior. | ||
É possível escrever um algoritmo mais eficiente. Ao invés de percorrer toda a rede e testar ponto a ponto pela possibilidade de uma transição, armazena-se em memória duas listas, uma de spins up e outra de spins down e sorteia-se dois elementos de cada lista para que se faça a transição. Dessa forma, não se perde tempo com rejeições. No entanto, para sistemas pequenos com alguns milhares de passos de Monte Carlo e relativamente poucos pontos como o sistema estudado não foi necessário esse ganho de performance. | |||
===Interface circular=== | ===Interface circular=== | ||
Nesse sistema exclui-se a condição de contorno que fixa os spins das paredes superior e inferior e atribui-se a elas as mesmas condições das paredes laterais, ou seja, condições de contorno periódicas onde, por exemplo, uma partícula na linha <math>l-1</math> pode trocar de lugar com sua primeira vizinha da linha <math>0</math> | |||
Como condição inicial posiciona-se as partículas num formato quadrado no centro da rede e observa-se como o formato da interface varia ao longo da simulação. A densidade de partículas é | Como condição inicial posiciona-se as partículas num formato quadrado no centro da rede e observa-se como o formato da interface varia ao longo da simulação. A densidade de partículas é menor que no exemplo anterior da interface linear. | ||
[[Arquivo:copSquare500iterinstepsof10.gif|frame|center|Interface circular entre sólido e vapor. Cada frame corresponde a 10 passos de Monte Carlo de um total de 500 passos. Primeira simulação com alta temperatura <math>T > T_C</math>. Segunda simução com temperatura intermediária <math>T < T_C</math>. Terceira simulação com baixa temperatura <math>T \ll T_C</math>]] | [[Arquivo:copSquare500iterinstepsof10.gif|frame|center|Interface circular entre sólido e vapor. Cada frame corresponde a 10 passos de Monte Carlo de um total de 500 passos. Primeira simulação com alta temperatura <math>T > T_C</math>. Segunda simução com temperatura intermediária <math>T < T_C</math>. Terceira simulação com baixa temperatura <math>T \ll T_C</math>]] | ||
Edição atual tal como às 07h32min de 25 de janeiro de 2018
Introdução
O modelo de Ising possui características universais que permitem aplicá-lo a situações diversas sendo tão versátil a ponto de descrever desde ferromagnetos até interações sociais. Dentro dessa gama de possibilidades existe o modelo de Conservação do Parâmetro de Ordem (CPO) em que, como o nome indica, mantém-se o parâmetro de ordem constante. No caso de um ferromagneto o parâmetro de ordem é a magnetização, portanto, um modelo de Ising sujeito CPO a grandeza análoga à magnetização se manteria constante a cada passo da simulação.
Apesar da estrutura matemática muito similar ao modelo de Ising, o modelo de CPO com sua simples condição de conservação do parâmetro de ordem aliado a condições de contorno permite que se modele sistemas marcadamente diferentes do tradicional sistema de ferromagneto tais como o gás de rede onde é possível estudar o comportamento de interfaces vapor-sólido ou vapor-líquido em condições de equilíbrio como por exemplo o equilíbrio entre água líquida e seu vapor ou entre gelo e vapor d'água.
O gás de rede é um modelo simplificado de um gás real onde se associa a cada ponto da rede uma partícula (átomo) ou sua ausência (vacância). Ao contrário do gás real a coordenada do movimento não é contínua, pois as partículas se movem de maneira discreta somente pelos vértices da rede. Pode-se refinar o modelo de diversas formas:
- Atribuindo inércia às partículas
- Alterando a forma da rede (quadrada, hexagonal, fcc, bcc, cúbica)
- Incluindo partículas de tipos diferentes com interações comum a seu respectivo tipo
- Presença e/ou tipos de colisões
No entanto, uma versão simplificada (e simples de simular) desse modelo é suficiente para reproduzir qualitativamente o comportamento de interfaces.
Teoria[1][2]
No modelo simplificado do gás de rede as partículas (sem inércia), movem-se de forma aleatória sob excitação térmica e satisfazem as seguintes condições:
- O número total de partículas é fixo: nenhuma partícula deixa ou entra no sistema, portanto, caso desapareça a partícula deve reaparecer em outro ponto da rede no mesmo passo de simulação.
- Um ponto da rede pode ser ocupado por uma única partícula ou permanecer vazio (não ocupado). Essa é uma maneira grosseira de assimilar o caráter físico de repulsão do gás real onde partículas não podem interpenetrar-se devido a exclusão de Pauli.
- Se duas partículas são primeiras vizinhas uma da outra elas sentem uma atração que é a mesma para qualquer par de partículas. Essa condição modela o efeito de atração entre partículas de um gás real.
As forças de atração e repulsão num gás real não possuem alcance de mesma ordem. A repulsão é de curto alcance enquanto a atração é de longo-alcance. Embora o presente modelo trate as partículas como se o alcance de repulsão e atração fossem da mesma ordem, ainda é possível extrair propriedades físicas que tem paralelo com o gás real tais como transições de fase e formato de interfaces.
A cada ponto da rede associamos o valor se houver uma partícula nesse ponto ou caso contrário. Representamos essa variável por , ou seja, no iésimo ponto da rede a variável pode assumir apenas os valores ou , ou resumidamente:
A conservação do número de partículas exige que se tenha:
Onde é a densidade de partículas e é o número total de partículas, sendo, portanto, o número de pontos ocupados da rede.
O hamiltoniano do sistema é modelado a partir da condição 2 exposta acima em que é especificado que um par de primeiros vizinhos na rede contribui para a diminuição da energia do sistema por uma quantidade :
Onde denota soma sobre todos os pares de primeiros vizinhos da rede.
Equivalência ao modelo de Ising
Para mostrar a equivalência com o modelo de Ising definimos a seguinte variável:
Essa nova variável é nada mais do que o spin no modelo de Ising para um ferromagneto assumindo os valores:
- quando , ou seja, posição ocupada por partícula; ou
- quando , ou seja, posição não ocupada
Em termos da variável de spin é dada por:
Substituindo no Hamiltoniano tem-se:
Seja o número de coordenação da rede, ou seja, o número de primeiros vizinhos ( para rede quadrada e para rede cúbica simples). Para uma dada rede existem <math\frac{1}{2}z N</math> possíveis pares distintos de primeiros vizinhos
Pode-se simplificar esssa expressão com base nas seguintes observações:
- Os somatórios em e são idênticos exceto pelo índice.
- A soma sobre pares de vizinhos é equivalente a somar vezes sobre o número de pontos da rede:
- pode ser escrito em termos das constantes e assim como ocorre com
Dessa forma o Hamiltoniano se reduz a:
Seja J = e observando que é uma constante pois todos seus termos são constantes, chegamos na equivalência com o Hamiltoniano do modelo de Ising na ausência de campo magnético:
O valor esperado de qualquer quantidade física não é alterado pela adição de uma constante ao hamiltoniano:
Conservação do parâmetro de ordem
A magnetização do sistema é nada mais do que a soma de spins que já calculamos acima:
No entanto, e devem permanecer constantes durante toda a simução, isso implica que a magnetização também é sempre constante, ou seja, a magnetização é o parâmetro de ordem conservado nesse sistema fato que dá nome ao método.
É vantajoso tratar o modelo de gás de rede sob a perspectiva de um modelo de Ising pois todo o arcabouço de técnicas amplamente conhecidas e extensivamente estudadas para o modelo de Ising podem ser aplicadas.
Apesar das similaridades, o gás de rede, como definido, possui muito menos estados válidos () pois não é permitido alterar a magnetização do sistema enquanto no modelo de Ising qualquer spin individual pode ser invertido sem restrições pois a magnetização não precisa se manter constante ( estados possíveis).
Transição de fase
Aproveitando a equivalência estabelecida entre gás de rede e o modelo de Ising sabe-se que o sistema possui uma transição de fase que ocorre a uma temperatura crítica . Rearranjando a densidade de pontos (equivalente agora à densidade de spins up) tem-se:
No modelo de Ising sabe-se também que abaixo da temperatura crítica existem dois valores de equilíbrio para a magnetização que são e , portanto, para favorecer a coexistência de fases tem-se que:
Para valores de fora do intervalo ainda é possível que uma região do sistema favoreça uma das duas densidades preferenciais. Suponha que se tenha . Nesse caso o sistema possui menos partículas do que precisa pra atingir o a densidade . Ainda que localmente seja possível o sistema atingir a densidade isso leva a uma falta ainda maior de partículas em outras regiões do sistema sendo, portanto, energeticamente custoso. A opção energeticamente mais favorável adotada pelo sistema é distribuir as poucas partículas homegeneamente pela rede. Esse comportamento é observado na simulação.
Dessa forma, no caso de o sistema possui duas fases:
- Uma em que se dividindo em dois domínios cada qual favorecendo uma das duas densidades
- E outra em que tendo densidade homogênea
Com sujeito ao intervalo conclui-se que pode assumir um intervalo menor de valores a medida que diminui. A magnetização diminui sob o aumento da temperatura. Acima da temperatura crítica a e portanto o intervalo reduz-se a zero evidenciando que não existe mais um valor de que evite a homogeinização da rede.
A discussão acima pode ser apresentada resumidamente pelo diagrama de fases:
Esse comportamento é observado quando se diminui a temperatura de vapor d'agua que passa a formar gotas líquidas que coexistem com o vapor para um intervalo de temperaturas. A fase condensada do gás de rede, no entanto, é mais adequadamente interpretada como um sólido devido a posição fixa das partículas (análogas a moléculas ou átomos) na rede, dessa forma, falamos de interface vapor/sólido ao invés de vapor/líquido.
Teoria[1][2]
Sistemas físicos em equilíbrio com muitos graus de liberdade e no limite termodinâmico comportam-se de tal forma que ao flutuarem de um estado para um estado tem-se que difere pouco de . Outra maneira de dizer isso é que as flutuações dessa tipo de sistema físico são muito pequenas em relação ao número de configurações possíveis e que portanto o sistema passa a maior parte do tempo alternando entre um pequeno conjunto de configurações. A consequência disso é que pode-se escolher uma estratégia de visitar com maior probabilidade apenas a fração de estados do sistema, as quais mais contribuem para atingir o equilíbrio ao invés de se visitar todos os estados indistintamente. No modelo de ferromagneto, por exemplo, com uma rede , há configurações possíveis sendo que mesmo com um supercomputador seria impraticável realizar essa simulação. O método de Monte Carlo consiste em visitar eficientemente uma pequena fração desses estados e atingir rapidamente o equilíbrio em poucos passos e o peso que define como visitar o estado seguinte é dado pela distribuição de Boltzmann onde fica claro que quanto mais diferente for de menor a change de fazer a transição
Dessa forma impõe-se que no equilíbrio o sistema obedeça a distribuição de Boltzmann, portanto a condição de balanço detalhado dá liberdade na escolha de e desde que seja satisfeita:
Uma possível escolha para seria:
Tomando e como é cancelada na razão entre probabilidades de aceitação temos a liberdade na sua escolha desde que mantenha a probabilidade menor ou igual a um. No modelo de ferromagneto, por exemplo, a maior diferença de energia que se pode obter entre estados é o que significa que o maior valor de é justamente . Assim, para garantir que a probabilidade seja menor ou igual a 1 deve-se escolher
Para que o algoritmo seja eficiente deseja-se que a probabilidade de aceitação seja a maior possível, pois do contrário estaríamos utilizando tempo computacional apenas para rejeitar trocas de estado. Portanto queremos que assuma o maior valor possível , maximizando :
Devido a condição de balanço detalhado, essa escolha implica:
Metropolis percebeu que desde que a condição de balanço detalhado seja satisfeita tem-se liberdade na escolha das probabilidades de aceitação. Então ele decidiu atribuir o maior valor possível para a probabilidade de aceitação que tem o maior valor entre as duas, no caso , ou seja:
O que implica:
Dessa forma a transição de estados sempre ocorre se ou seja mas pode ou não ocorrer caso seja com uma probabilidade dada por . Em suma:
Implementação[1]
Para obedecer a condição de conservação da magnetização não é permitido alterar um spin individualmente (ou um número ímpar de spins). Uma maneira de tratar a dinâmica desse sistema foi proposta por Kawasaki [3] e consiste em simplesmente alternar o estado de spin de um par de partículas que tenham estados de spin oposto, ou seja:
É evidente que nesse caso a mudança conserva a magnetização, pois a troca de spins resulta em variação de magnetização nula.
Cada ponto da rede possui vizinhos e portanto a cada passo de iteração deve-se sortear com qual dos vizinhos será feita uma tentativa de troca de spins. Essa escolha é feita aleatoriamente (uniforme). Uma vez escolhido um vizinho deve-se decidir se a troca deve ser feita ou não. Essa decisão é tomada com base no método de Monte Carlo, em particular, com a probabilidade de aceitação de Metropolis exatamente como exposto na seção acima.
A ergodicidade é satisfeita pelo sistema pois um passo de Monte Carlo corresponde a uma troca entre vizinhos que numa rede finita pode ser efetuada a partir de outro estado qualquer em número finito de passos
Como já foi mencionado a rede possui pontos e número de coordenação o que resulta em pares de primeiros vizinhos, portanto, a probabilidade de selecionar um par qualquer é dada por:
A probabilidade de seleção é a mesma fazendo com que esses termos se cortem na condição de balanço detalhado e permitindo que se aplique a escolha de Metropolis discutida acima sem alterações.
Para efetivamente tomar a decisão sobre a troca entre vizinhos onde é necessário especificar como é feito seu cálculo. é dado pela seguinte expressão:
Seja um ponto da rede e primeiro vizinho de . Deseja-se calcular a energia de interação entre esse par. A expressão acima apenas diz que deve-somar os produtos do spin de , , com seus primeiros vizinhos excluindo-se da soma tanto quanto . Faz-se o mesmo procedimento para , ou seja, soma-se os produtos do spin , , com todos os seus primeiros vizinhos exceto ele mesmo e . A soma dessas duas quantidades multiplicadas por é igual a diferença de energia entre a configuração e a
A simulação é extremamente simplificada pelo fato de o estado final não figurar na expressão para o cálculo da diferença de energia da transição, pois pode-se verificar de antemão se a transição deve ser feita sem que seja necessário efetivamente colocar o sistema no estado final .
Simulação
Foram simulados três sistemas diferentes os quais são discutidos a seguir. O objetivo das simulações em determinar a tendência do formato de cada interface após vários passos de monte carlo sem verificar rigorosamente se o equilíbrio foi atingido. Uma análise das condições de equilíbrio é discutida na última seção. Todas as simulações demandam a geração de muitos números aleatórios por isso optou-se por usar Mersenne Twister - um algoritmo veloz para geração de números aleatórios.
Interface linear
Esse sistema consiste de uma rede quadrada de aresta . A rede tem inicialmente sua metade inferior completamente populada por partículas (spins up) e o restante da rede possui vacâncias (spins down).
Cada ponto da rede é visitado sequencialmente e um dos seus 4 vizinhos é sorteado para que se faça uma tentativa de troca de posição entre o par. Caso a energia do sistema diminua, a troca é feita com probabilidade 1. Caso contrário a troca ocorre com probabilidade dada pelo peso de Boltzmann (algoritmo de Metropolis).
A primeira condição de contorno refere-se às paredes superior e inferior. A ultima linha de pontos da rede possui spins apontando pra baixo permanentemente assim como a primeira linha de pontos da rede tem-se spins apontando pra cima. Para que essa configuração seja mantida ao longo da simulação, evita-se qualquer tentativa de troca entre pares envolvendo esses pontos. Essa condição de contorno garante que a interface se mantenha fixa, do contrário, ela poderia transitar pela rede. Nas paredes laterais aplica-se condição de contorno periódica onde por exemplo um ponto da rede na coluna pode trocar de lugar com um primeiro vizinho da coluna e vice-versa.
Ao iterar pela rede é comum deparar-se com pares de vizinhos que possuem mesma orientação de spin e portanto são ignorados imediatamente pois em nada contribuem para a dinâmica do sistema.
Como observado, a alta temperatura recai-se no regime homogêneo em que a alternativa mais adequada para que o sistema minize sua energia é distribuir os spins up (partículas) uniformemente pela rede. A uma temperatura abaixo da crítica percebe-se a formação de uma interface persistente entre a região inferior com densidade preferencial e a superior com densidade preferencial em coexistência. Ao diminuir ainda mais a temperatura o efeito fica mais acentuado, ou seja, a interface é menos deformada em relação ao caso anterior.
É possível escrever um algoritmo mais eficiente. Ao invés de percorrer toda a rede e testar ponto a ponto pela possibilidade de uma transição, armazena-se em memória duas listas, uma de spins up e outra de spins down e sorteia-se dois elementos de cada lista para que se faça a transição. Dessa forma, não se perde tempo com rejeições. No entanto, para sistemas pequenos com alguns milhares de passos de Monte Carlo e relativamente poucos pontos como o sistema estudado não foi necessário esse ganho de performance.
Interface circular
Nesse sistema exclui-se a condição de contorno que fixa os spins das paredes superior e inferior e atribui-se a elas as mesmas condições das paredes laterais, ou seja, condições de contorno periódicas onde, por exemplo, uma partícula na linha pode trocar de lugar com sua primeira vizinha da linha Como condição inicial posiciona-se as partículas num formato quadrado no centro da rede e observa-se como o formato da interface varia ao longo da simulação. A densidade de partículas é menor que no exemplo anterior da interface linear.
A interface é energeticamente custosa pois para cada par de spins antialinhados o sistema aumenta de energia por um fator 2J e como na rede quadrada um spin da interface possui 3 vizinhos antialinhados, sistema aumenta de energia por um fator 6J. Portanto fisicamente espera-se que o sistema evolua de tal forma a minimizar a extensão da sua interface, minimizando sua tensão superficial. No caso simulado espera-se que um domínio circular seja gerado pois o círculo é a forma geométrica que possui menor perímetro. No entanto, como a simulação demonstra, mesmo pra baixas temperaturas a forma nunca é perfeitamente circular e isso se deve ao tamanho finito da rede o faz com que seu formato (da rede) influencie o formato da interface.
A animação abaixo ilustra o mesmo processo mas com menos frames por segundo permitindo acompanhar detalhes da dinâmica do sistema.
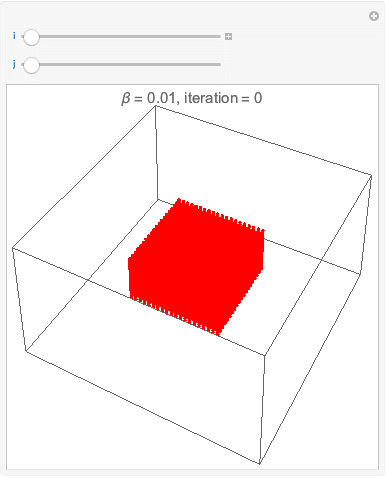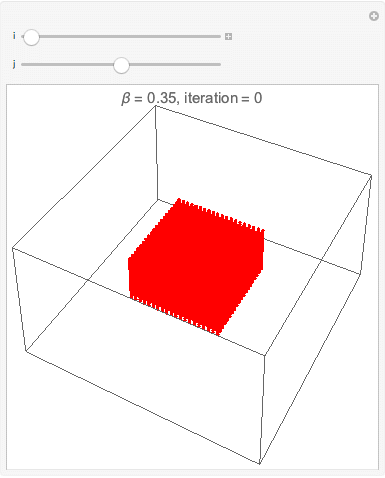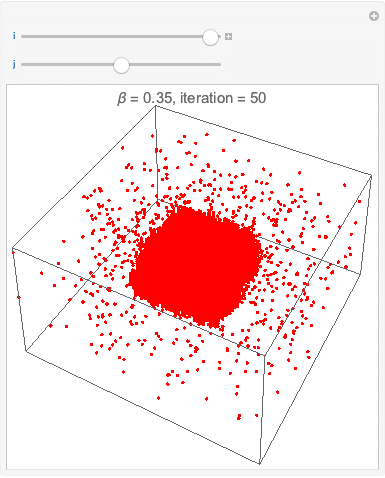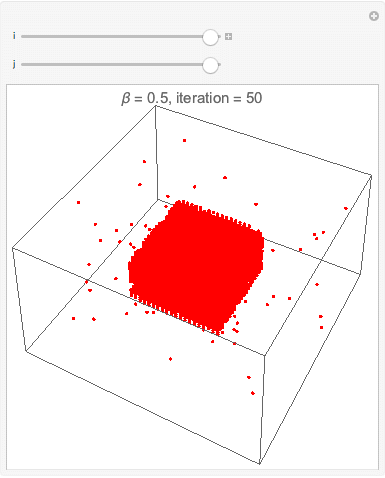
Interface esférica
A simulação da interface esférica é uma extensão direita da simulação da interface circular apenas adicionando mais uma dimensão. Observa-se os mesmos efeitos de redução de tensão superficial pela deformação do cubo em uma região aproximadamente esférica quando a temperatura é menor que a temperatura crítica. Acima da a temperatura crítica a densidade fica homogênea como esperado.
Cada ponto da rede agora possui 6 vizinhos ao invés de 4 e isso faz com que as haja valores adicionais de diferenças de energia entre estados (na rede quadrada era possível obter e agora na rede cúbica
A mesma simulação com menos partículas, vista mais distante e com uma pequena diferença na quantidade de passos.
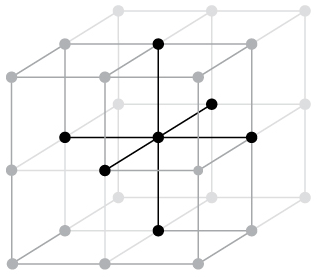
Introduzindo interações entre segundos vizinhos é possível reproduzir formatos de cristais cúbicos como por exemplo o cristal de face centrada ou de corpo centrado.[1]
Equilíbrio
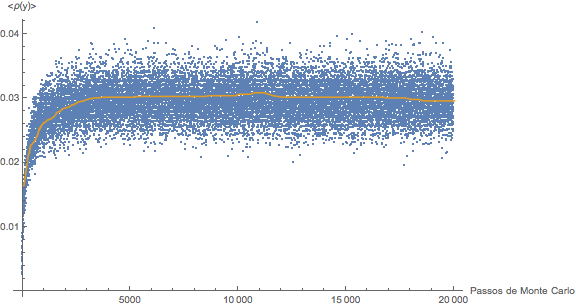
Para medir qualquer grandeza de um sistema simulado pelo método de Carlo é necessária que a medida seja feita sob regime de equilíbrio. Torna-se então importante saber quando o sistema atinge o equilíbrio. No caso de um ferromagneto no modelo de Ising pode-se monitorar a magnetização ou calor específico até que a grandeza atinja um valor estacionário. No caso do gás de rede podemos monitorar o formato da interface, ou mais simplesmente, a densidade média de spins up (partículas) em cada coluna da rede quadrada. Acompanhando a mudança percentual nessa densidade ao passar de um passo de Monte Carlo para o passo seguinte é possível ter uma idéia de quanto passos são necessários para atingir o equilíbrio.
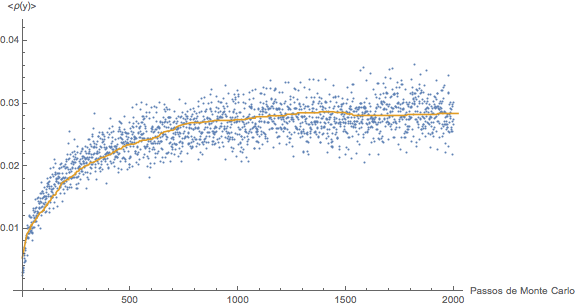
Olhando mais de perto o início da curva percebe-se que em torno de 1500 passos o equilíbrio ja foi seguramente atingido.
As simulações exibidas acima estão, portanto, na região fora do equilíbrio mas como observado acima o objetivo das simulações era determinar a tendência do formato das interfaces e não o seu formato no equilíbrio.
Códigos
Conservação de parâmetro de ordem - Interface linear
Conservação de parâmetro de ordem - Interface circular
Conservação de parâmetro de ordem - Interface esférica
Conservação de parâmetro de ordem - Equilíbrio
Bibliografia
- ↑ 1,0 1,1 1,2 1,3 Newman, M. E. J.; Barkema, G. T. (1999). "Monte Carlo Methods in Statistical Physics" New York: Oxford University Press. ISBN 019-851796-3.
- ↑ 2,0 2,1 Krauth, Werner (2006). "Statiscal Mechanics: Algorithms and Computations" New York: Oxford University Press. ISBN 978-0-19-851535-7.
- ↑ T. Ohta, D. Jasnow and K. Kawasaki, Phys. Rev. Lett. 49 1223 (1982). "Universal Scaling in the Motion of Random Interfaces". American Physical Society





















































![{\displaystyle \rho \in [\rho _{-},\rho _{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc499e595fcf8c8a7ff5bb02b94a9231e387d12d)

![{\displaystyle \rho \not \in [\rho _{-},\rho _{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c5527be819a2d89bab9d4105ca6dbf947319821)




































![{\displaystyle \Delta E=E_{\nu }-E_{\mu }=2J\left[s_{k}^{\mu }\sum _{i\not \in \{k',k\}}s_{i}^{\mu }+s_{k'}^{\mu }\sum _{j\not \in \{k,k'\}}s_{j}^{\mu }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa23051c87414cc6c8c16aaa2fd2255a1d1c79a9)