Equação de Klein-Gordon: mudanças entre as edições

De Física Computacional
Ir para navegação Ir para pesquisar
 
(33 revisões intermediárias por 3 usuários não estão sendo mostradas)
Linha 1: Linha 1:
== INTRODUÇÃO ==
== INTRODUÇÃO ==
A equação de Klein-Gordon é uma das equações fundamentais na teoria quântica relativística. Ela descreve partículas escalares (partículas sem spin, como os mésons, em seu modelo básico) e é uma extensão relativística da equação de Schrödinger, incorporando a relação de energia relativística de Einstein <math>E=p^2c^2 + m^2c^4 </math>. A equação é nomeada em homenagem a Oskar Klein e Walter Gordon, que a formularam independentemente. De maneira geral, a equação pode ser escrita como:
A equação de Klein-Gordon é uma das equações fundamentais na teoria quântica relativística. Ela descreve partículas escalares (partículas sem spin, como os bósons de Higgs) e é uma extensão relativística da equação de Schrödinger, incorporando a relação de energia relativística de Einstein <math>E=p^2c^2 + m^2c^4 </math>. A equação é nomeada em homenagem a Oskar Klein e Walter Gordon, que a formularam independentemente. De maneira geral, a equação pode ser escrita como:




Linha 12: Linha 12:


<math> \frac{\partial^2 \psi}{\partial t^2} = c^2 \frac{\partial^2\psi}{\partial x^2} - \frac{m^2 c^4}{\hbar^2} \psi</math> (em uma dimensão)
<math> \frac{\partial^2 \psi}{\partial t^2} = c^2 \frac{\partial^2\psi}{\partial x^2} - \frac{m^2 c^4}{\hbar^2} \psi</math> (em uma dimensão)
Inicialmente, a equação pode ser interpretada como uma equação de um campo escalar que pode ser quantizado, onde é introduzido um campo quantico que é descrito por partículas sem spin. No reino da física de partículas, as interações eletromagnéticas podem ser incorporadas formando o tópico da eletrodinâmica escalar, por exemplo. Entretando, a solução da equação não pode ser interpretada diretamente como a densidade de probabilidade vista na equação de Schrodinger, em vez disso, a densidade de probabilidade relativística é definida usando uma corrente de probabilidade associada. Na mecânica quântica relativística, a função de onda <math> \psi(x,t) </math> é usada para descrever o estado de uma partícula no espaço-tempo.


== MÉTODO DAS DIFERENÇAS FINITAS ==
== MÉTODO DAS DIFERENÇAS FINITAS ==
Linha 42: Linha 44:
ou, mais usualmente: <math>\psi_i^{n+1}  =  2\psi_i^n  - \psi_i^{n-1}  + \alpha^2 ( \psi_{i+1}^n - 2\psi_i^n + \psi_{i-1}^n) - \beta^2 \psi  </math>
ou, mais usualmente: <math>\psi_i^{n+1}  =  2\psi_i^n  - \psi_i^{n-1}  + \alpha^2 ( \psi_{i+1}^n - 2\psi_i^n + \psi_{i-1}^n) - \beta^2 \psi  </math>


== ESTABILIDADE ta errado, estou testando outras coisas ==
== CRITÉRIO DE ESTABILIDADE ==
 
 
Forma Contínua e Discretização: A equação de Klein-Gordon contínua é: <math> \frac{\partial^2 \psi}{\partial t^2} = c^2 \frac{\partial^2 \psi}{\partial x^2} - \frac{m^2 c^4}{\hbar^2} \psi. </math>
 
A forma discreta, usando diferenças finitas centralizadas no tempo e no espaço, é: <math> \psi_i^{n+1} = 2 \psi_i^n - \psi_i^{n-1} + \frac{c^2 \Delta t^2}{\Delta x^2} (\psi_{i+1}^n - 2 \psi_i^n + \psi_{i-1}^n) - \frac{m^2 c^4 \Delta t^2}{\hbar^2} \psi_i^n. </math> Aqui, definimos os coeficientes: <math> \alpha = \frac{c \Delta t}{\Delta x}, \quad \beta = \frac{m c^2 \Delta t}{\hbar}. </math>
 
Suposição de Solução Harmônica: Substituímos uma solução da forma: <math> \psi_i^n = G^n e^{i k x_i}, </math> onde:
 
na equação: <math> G^{n+1} e^{i k x_i} = 2 G^n e^{i k x_i} - G^{n-1} e^{i k x_i} + \alpha^2 G^n \left(e^{i k x_{i+1}} - 2 e^{i k x_i} + e^{i k x_{i-1}}\right) - \beta^2 G^n e^{i k x_i}. </math>
 
Simplificação:
 
Como <math> e^{i k x_{i+1}} = e^{i k x_i} e^{i k \Delta x} </math> e <math> e^{i k x_{i-1}} = e^{i k x_i} e^{-i k \Delta x} </math>, o termo centralizado se torna: <math> e^{i k x_{i+1}} - 2 e^{i k x_i} + e^{i k x_{i-1}} = e^{i k x_i} \left(e^{i k \Delta x} - 2 + e^{-i k \Delta x}\right). </math>
Usando <math> e^{i k \Delta x} + e^{-i k \Delta x} = 2 \cos(k \Delta x) </math>, temos: <math> e^{i k x_{i+1}} - 2 e^{i k x_i} + e^{i k x_{i-1}} = e^{i k x_i} \left(-2 + 2 \cos(k \Delta x)\right). </math>
Substituímos isso na equação e cancelamos o fator <math> e^{i k x_i} </math>, que nunca é zero: <math> G^{n+1} = 2 G^n - G^{n-1} - \alpha^2 (2 - 2 \cos(k \Delta x)) G^n - \beta^2 G^n. </math>
 
Simplificando mais, obtemos: <math> G^{n+1} = (2 - \alpha^2 (2 - 2 \cos(k \Delta x)) - \beta^2) G^n - G^{n-1}. </math>
 
Equação Característica: Assumimos uma solução na forma de uma equação quadrática <math> G </math>: <math> G^2 - G \left(2 - \alpha^2 (2 - 2 \cos(k \Delta x)) - \beta^2 \right) + 1 = 0. </math>
 
Condição de Estabilidade: Para estabilidade, as raízes de <math> G </math> devem satisfazer <math> |G| \leq 1 </math>. Isso leva ao critério: <math> \alpha \leq 1, \quad \text{ou seja,} \quad \frac{c \Delta t}{\Delta x} \leq 1. </math>
 
Conclusão Matemática:
A condição <math> \alpha \leq 1 </math> garante que os termos oscilatórios na solução não crescem exponencialmente. Essa análise também mostra que:
 
Quanto menor o passo de tempo <math> \Delta t </math>, mais precisa e estável é a solução.
A relação entre os passos de tempo e espaço é crucial: aumentar muito <math> \Delta t </math> sem ajustar <math> \Delta x </math> pode levar à instabilidade.
 
== C.C e C.I ==
 
Condições iniciais e condições de contorno são fundamentais para a resolução da equação, já que elas ditam o comportamento da função oa longo do tempo e ao longo do espaço, para plotar a evolução temporal, utilizarei as seguintes condições iniciais e de contorno:
 
<math> \psi(x,0) = Ae^{-\frac{x-x_0}{2\sigma^2}}</math> que define um pulso gaussiano como condição inicial.
 
e <math>\frac{\partial \psi(x,0)}{\partial t} =0 </math> que define que, no instante de tempo t=0, a função não possui velocidade inicial, o que implica que o pulso está parado inicialmente e sua evolução se deve pela propagação de flutuações espaciais.
 
Nesta condição, A é a altura do pulso, <math> x_0 </math> é a posição central do pulso e <math> \sigma </math> é a largura do pulso.
 
Utilizarei também as condições de contorno em que <math>\psi(0,t)= 0 </math> e <math>\psi(L,t)=0 </math> o que garante que a função 'morra' nas pontas.
 
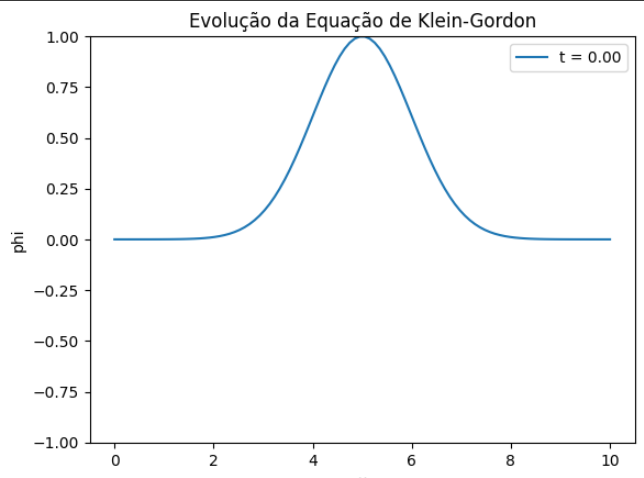
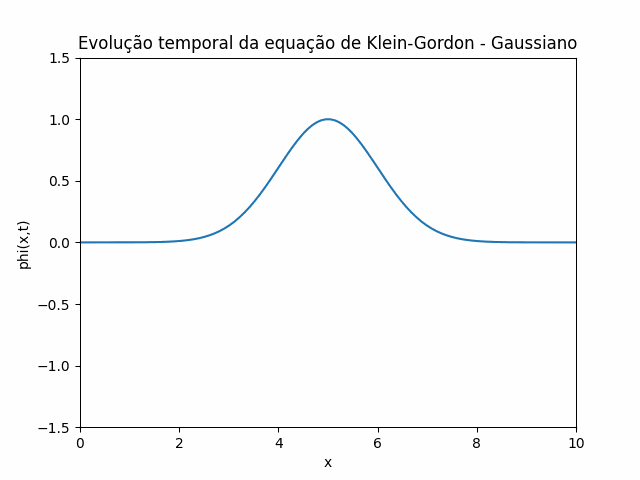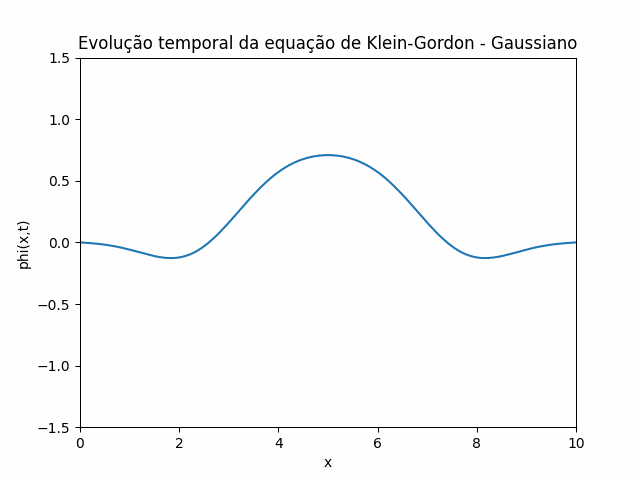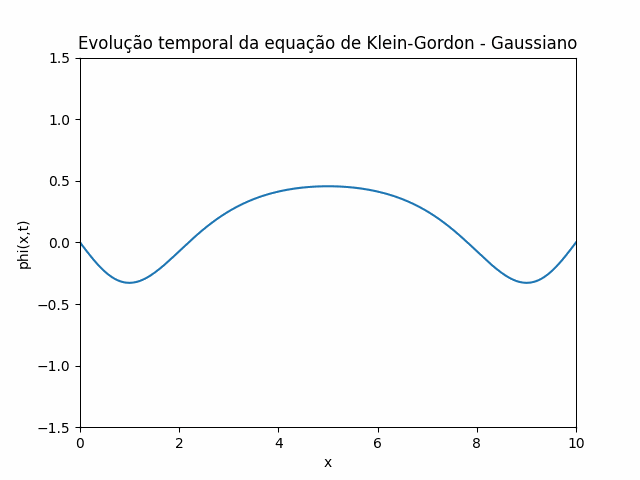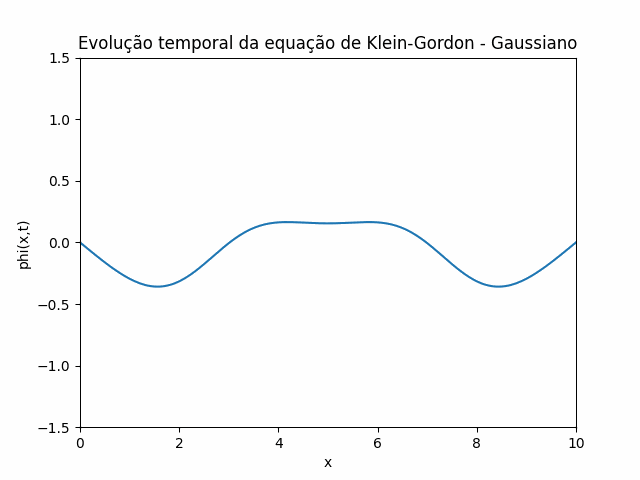
Utilizando estas condições iniciais e condições de contorno, foi feito um gif que mostra a evolução temporal da equação de Klein-Gordon utilizando o método das diferenças finitas:
 
[[Arquivo:Estatico.png]]
 
[[Arquivo:Klein 2.gif]]
 
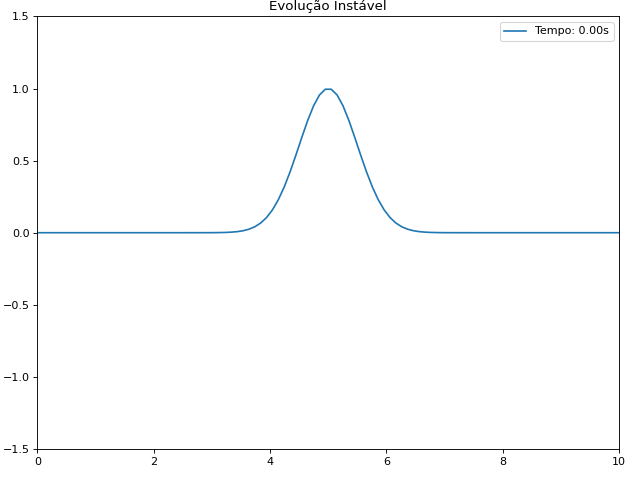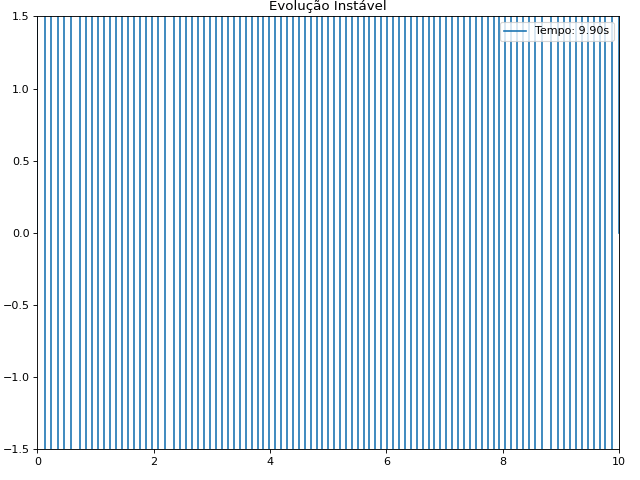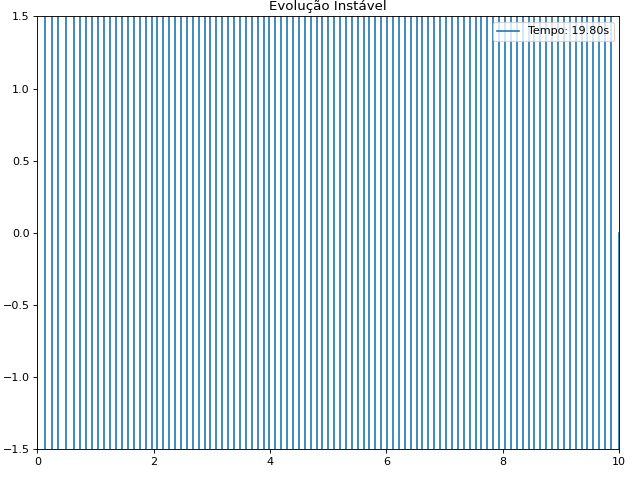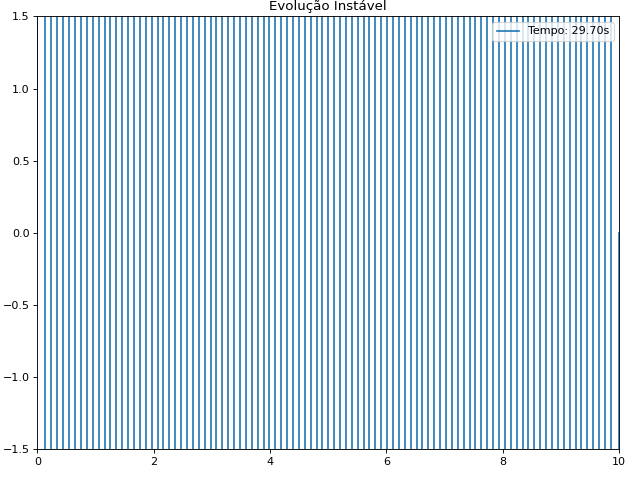
[[Arquivo:Estabilidade.gif]]
 
 
Localização Inicial: No gráfico mostrado, <math> \psi(x,t) </math> tem um pico bem definido, o que sugere que a partícula está localizada inicialmente em torno de um ponto central no espaço. Isso significa que a probabilidade da partícula estar presente é maior nessa região (em torno do pico), e diminui nas bordas. No gráfico mostrado acima, <math> \psi(x,t) </math> tem um pico bem definido, o que sugere que a partícula está localizada inicialmente em torno de um ponto central no espaço. Isso significa que a probabilidade da partícula estar presente é maior nessa região (em torno do pico), e diminui nas bordas.
 
 
= Código utilizado =
 
import numpy as np
 
import matplotlib.pyplot as plt
 
from matplotlib.animation import FuncAnimation
 
 
L = 10.0          # Comprimento da simulação
 
Nx = 100          # Número de pontos espaciais
 
dx = L / Nx      # Passo espacial
 
T_max = 30        # Tempo máximo de simulação
 
m = 1.0          # Massa da partícula


Para analisar a estabilidade do método utilizaremos os Modos de Furrier.
c = 1.0          # Velocidade da luz


<math> \psi_i^{n+1} = 2\psi_i^n - \psi_i^{n-1} + \alpha^2 \left( \psi_{i+1}^n - 2\psi_i^n + \psi_{i-1}^n \right) - \beta^2 \psi_i^n </math>.
hbar = 1.0        # Constante de Planck reduzida




sendo <math>\psi_i^n = A^n e^{i k i \Delta x} </math> o Modo de Furrier.
A = 1.0          # Amplitude do pulso


x0 = L / 2        # Posição central do pulso


Substituímos <math>\psi_i^n, \psi_{i+1}^n</math>, e <math>\psi_{i-1}^n </math>na equação:
sigma = 0.5      # Largura do pulso


<math>\psi_{i+1}^n = A^n e^{i k (i+1) \Delta x} = A^n e^{i k i \Delta x} e^{i k \Delta x}</math>


<math>\psi_{i-1}^n = A^n e^{i k (i-1) \Delta x} = A^n e^{i k i \Delta x} e^{-i k \Delta x}</math>
x = np.linspace(0, L, Nx)


Usamos a identidade <math> e^{i k \Delta x} + e^{-i k \Delta x} = 2 \cos(k \Delta x) </math>:


<math> A^{n+1} = 2A^n - A^{n-1} + \alpha^2 \left[ 2 \cos(k \Delta x) - 2 \right] A^n - \beta^2 A^n </math>
phi_0 = A * np.exp(-((x - x0)**2) / (2 * sigma**2))


Fatoramos:
dphi_0 = np.zeros(Nx)  # Derivada inicial nula


<math> A^{n+1} = \left( 2 - 2\alpha^2 - \beta^2 + 2\alpha^2 \cos(k \Delta x) \right) A^n - A^{n-1}. </math>
#estabilidade
alpha_stable = 0.5  # Valor estável para alpha (c * dt / dx)


A relação de recorrência é:
dt_stable = alpha_stable * dx / c


<math> A^{n+1} - \lambda A^n + A^{n-1} = 0 </math>
alpha_unstable = 1.5  # Valor instável para alpha (c * dt / dx)


onde
dt_unstable = alpha_unstable * dx / c


<math> \lambda = 2 - 2\alpha^2 - \beta^2 + 2\alpha^2 \cos(k \Delta x) </math>.


Definimos <math> \mu= |\frac{A^{n+1}}{A^n} | </math> como sendo o fator de amplificação. Assim, a equação fica <math> \mu A^n=\lambda A^n - A^n \frac{A^{n-1}}{A^n} </math>
Nt_stable = int(T_max / dt_stable)


Dividindo tudo por <math> A^n </math> : <math> \mu = \lambda - \frac{1}{\mu} </math>
Nt_unstable = int(T_max / dt_unstable)


Portanto, a equação característica associada é:


<math> \mu^2 - \lambda \mu + 1 = 0 </math>
def evolve_wave(dt, Nt):


onde <math> \mu </math> são as raízes que representam o fator de amplificação <math> \mu= |\frac{A^{n+1}}{A^n} | </math>.
    phi = np.zeros((Nt, Nx))


Para que o método seja estável, as raízes <math>\mu</math> devem satisfazer <math>\|\mu| \leq 1</math>. Isso é garantido se o discriminante da equação característica satisfizer:
    phi[0, :] = phi_0


<math> \lambda^2 - 4 \leq 0 </math>.
    phi[1, :] = phi_0 + dt * dphi_0


Substituímos <math>\lambda </math>:


<math> \left( 2 - 2\alpha^2 - \beta^2 + 2\alpha^2 \cos(k \Delta x) \right)^2 - 4 \leq 0 </math>.
    for n in range(1, Nt-1):


O caso crítico ocorre para o maior valor de <math>cos(k \Delta x)</math>, que é <math>cos(k \Delta x) = 1</math>, e o menor valor, <math>cos(k \Delta x) = -1</math>:
        for i in range(1, Nx-1):


<math>cos(k \Delta x) = 1 </math>:
            phi[n+1, i] = 2 * phi[n, i] - phi[n-1, i] + (dt**2) * (
   
<math>\lambda = 2 - 2\alpha^2 - \beta^2 + 2\alpha^2</math>.
 
Isso simplifica para:
 
<math>  \lambda = 2 - \beta^2 </math>
 
Para estabilidade:
 
<math>  (2 - \beta^2)^2 - 4 \leq 0 </math>.
   
<math>  \beta \geq 0 </math>.
   
Para <math> cos(k \Delta x) = -1</math>:
   
<math>\lambda = 2 - 2\alpha^2 - \beta^2 - 2\alpha^2</math>.
   
<math> \lambda = 2 - 4\alpha^2 - \beta^2 </math>.
 
Ou seja, para que seja estável:
 
<math> (2 - 4\alpha^2 - \beta^2)^2 - 4 \leq 0 </math>.
 
Após expandir:
   
<math> \alpha \geq \frac{\beta}{2} </math>.
   
A condição de estabilidade combinada é:


<math> \alpha \geq \frac{\beta}{2} </math>
                (phi[n, i+1] - 2 * phi[n, i] + phi[n, i-1]) / dx**2
e  <math> \beta \geq 0  </math> .


Essas desigualdades controlam os passos de tempo e espaço, garantindo a estabilidade do método.
                - (m**2 * c**2 / hbar**2) * phi[n, i]
            )


    return phi




phi_stable = evolve_wave(dt_stable, Nt_stable)


== CRITÉRIO DE ESTABILIDADE ==
phi_unstable = evolve_wave(dt_unstable, Nt_unstable)
 
 
fig, ax = plt.subplots(2, 1, figsize=(10, 8))
 
 
def update_stable(frame):
 
    ax[0].cla()
 
    ax[0].plot(x, phi_stable[frame, :], label=f'Tempo: {frame * dt_stable:.2f}s')
 
    ax[0].set_title("Evolução Estável")
 
    ax[0].set_xlim(0, L)
 
    ax[0].set_ylim(-1.5, 1.5)
 
    ax[0].legend()
 
 
def update_unstable(frame):
 
    ax[1].cla()
 
    ax[1].plot(x, phi_unstable[frame, :], label=f'Tempo: {frame * dt_unstable:.2f}s')
 
    ax[1].set_title("Evolução Instável")
 
    ax[1].set_xlim(0, L)


    ax[1].set_ylim(-1.5, 1.5)


A Forma Contínua e Eiscretização da equação de Klein-Gordon contínua é: <math> \frac{\partial^2 \psi}{\partial t^2} = c^2 \frac{\partial^2 \psi}{\partial x^2} - \frac{m^2 c^4}{\hbar^2} \psi. </math>
    ax[1].legend()


A forma discreta, usando diferenças finitas centralizadas no tempo e no espaço, é: <math> \psi_i^{n+1} = 2 \psi_i^n - \psi_i^{n-1} + \frac{c^2 \Delta t^2}{\Delta x^2} (\psi_{i+1}^n - 2 \psi_i^n + \psi_{i-1}^n) - \frac{m^2 c^4 \Delta t^2}{\hbar^2} \psi_i^n. </math> Aqui, definimos os coeficientes: <math> \alpha = \frac{c \Delta t}{\Delta x}, \quad \beta = \frac{m c^2 \Delta t}{\hbar}. </math>


Suposição de Solução Harmônica: Substituímos uma solução da forma: <math> \psi_i^n = G^n e^{i k x_i}, </math> onde:
def init():


  na equação: <math> G^{n+1} e^{i k x_i} = 2 G^n e^{i k x_i} - G^{n-1} e^{i k x_i} + \alpha^2 G^n \left(e^{i k x_{i+1}} - 2 e^{i k x_i} + e^{i k x_{i-1}}\right) - \beta^2 G^n e^{i k x_i}. </math>
    for a in ax:


Simplificação:
        a.clear()


Como <math> e^{i k x_{i+1}} = e^{i k x_i} e^{i k \Delta x} </math> e <math> e^{i k x_{i-1}} = e^{i k x_i} e^{-i k \Delta x} </math>, o termo centralizado se torna: <math> e^{i k x_{i+1}} - 2 e^{i k x_i} + e^{i k x_{i-1}} = e^{i k x_i} \left(e^{i k \Delta x} - 2 + e^{-i k \Delta x}\right). </math>
    return ax
Usando <math> e^{i k \Delta x} + e^{-i k \Delta x} = 2 \cos(k \Delta x) </math>, temos: <math> e^{i k x_{i+1}} - 2 e^{i k x_i} + e^{i k x_{i-1}} = e^{i k x_i} \left(-2 + 2 \cos(k \Delta x)\right). </math>
Substituímos isso na equação e cancelamos o fator <math> e^{i k x_i} </math>, que nunca é zero: <math> G^{n+1} = 2 G^n - G^{n-1} - \alpha^2 (2 - 2 \cos(k \Delta x)) G^n - \beta^2 G^n. </math>


Simplificando mais, obtemos: <math> G^{n+1} = (2 - \alpha^2 (2 - 2 \cos(k \Delta x)) - \beta^2) G^n - G^{n-1}. </math>
# Atualização combinada para animação
def update(frame):


Equação Característica: Assumimos uma solução da forma <math> G^n = G^n </math> e obtemos uma equação quadrática para <math> G </math>: <math> G^2 - G \left(2 - \alpha^2 (2 - 2 \cos(k \Delta x)) - \beta^2 \right) + 1 = 0. </math>
    update_stable(frame)


Condição de Estabilidade: Para estabilidade, as raízes de <math> G </math> devem satisfazer <math> |G| \leq 1 </math>. Isso leva ao critério: <math> \alpha \leq 1, \quad \text{ou seja,} \quad \frac{c \Delta t}{\Delta x} \leq 1. </math>
    update_unstable(frame)


Conclusão Matemática
    return ax
A condição <math> \alpha \leq 1 </math> garante que os termos oscilatórios na solução não crescem exponencialmente. Essa análise também mostra que:


Quanto menor o passo de tempo <math> \Delta t </math>, mais precisa e estável é a solução.
# Criando a animação
A relação entre os passos de tempo e espaço é crucial: aumentar muito <math> \Delta t </math> sem ajustar <math> \Delta x </math> pode levar à instabilidade.
frames_stable = range(0, Nt_stable, max(1, Nt_stable // 150))


== C.C e C.I ==
frames_unstable = range(0, Nt_unstable, max(1, Nt_unstable // 150))


Condições iniciais e condições de contorno são fundamentais para a resolução da equação, já que elas ditam o comportamento da função oa longo do tempo e ao longo do espaço, para plotar a evolução temporal, utilizarei as seguintes condilções iniciais e de contorno:
ani = FuncAnimation(fig, update, frames=min(len(frames_stable), len(frames_unstable)),


<math> \psi(x,0) = Ae^{-\frac{x-x_0}{2\sigma^2}}</math> que define um pulso gaussiano como condição inicial.
init_func=init, blit=False)


e <math>\frac{\partial \psi(x,0)}{\partial t} =0 </math> que define que, no instante de tempo t=0, a função não possui velocidade inicial, o que implica que o pulso está parado inicialmente e sua evolução se deve pela propagação de flutuações espaciais.


Nesta condição, A é a altura do pulso, <math> x_0 </math> é a posição central do pulso e <math> \sigma </math> é a largura do pulso.
# Salvando as animações


Utilizarei também as condições de contorno em que <math>\psi(0,t)= 0 </math> e <math>\psi(L,t)=0 </math> o que garante que a função 'morra' nas pontas.
fig.tight_layout()


Utilizando estas condições iniciais e condições de contorno, foi feito um gif que mostra a evolução temporal da equação de Klein-Gordon utilizando o método das diferenças finitas:
ani.save('klein_gordon_stable_vs_unstable.gif', writer='pillow', fps=30)


[[Arquivo:Klein 2.gif]]
plt.show()

Edição atual tal como às 14h21min de 8 de janeiro de 2025

INTRODUÇÃO

A equação de Klein-Gordon é uma das equações fundamentais na teoria quântica relativística. Ela descreve partículas escalares (partículas sem spin, como os bósons de Higgs) e é uma extensão relativística da equação de Schrödinger, incorporando a relação de energia relativística de Einstein Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=p^2c^2 + m^2c^4 } . A equação é nomeada em homenagem a Oskar Klein e Walter Gordon, que a formularam independentemente. De maneira geral, a equação pode ser escrita como:


Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( \Box + \frac{m^2 c^2}{\hbar^2} \right) \psi(x,t)= 0 }

onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( \Box = \frac{\partial^2}{c^2\partial t^2} -\nabla^2 \right) } é chamado operador de d'Alambert.

Abrindo a equação, é obtido:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^2 \psi}{\partial t^2} = c^2 \nabla^2 \psi - \frac{m^2 c^4}{\hbar^2} \psi}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^2 \psi}{\partial t^2} = c^2 \frac{\partial^2\psi}{\partial x^2} - \frac{m^2 c^4}{\hbar^2} \psi} (em uma dimensão)

Inicialmente, a equação pode ser interpretada como uma equação de um campo escalar que pode ser quantizado, onde é introduzido um campo quantico que é descrito por partículas sem spin. No reino da física de partículas, as interações eletromagnéticas podem ser incorporadas formando o tópico da eletrodinâmica escalar, por exemplo. Entretando, a solução da equação não pode ser interpretada diretamente como a densidade de probabilidade vista na equação de Schrodinger, em vez disso, a densidade de probabilidade relativística é definida usando uma corrente de probabilidade associada. Na mecânica quântica relativística, a função de onda Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x,t) } é usada para descrever o estado de uma partícula no espaço-tempo.

MÉTODO DAS DIFERENÇAS FINITAS

O método das diferenças finitas é uma técnica numérica amplamente utilizada para resolver EDPs. Ele envolve a discretização das variáveis contínuas (geralmente no tempo ou no espaço), transformando as equações diferenciais em sistemas algébricos que podem ser resolvidos numericamente. Os primeiros passos para utilizar o método é fazer a discretização no tempo e no espaço. Para uma equação no tempo você discretiza o tempo em intervalos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta t } criando uma sequência de pontos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_n=n\Delta t } . Para uma equação no espaço você discretiza o espaço em intervalos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x } criando uma sequência de pontos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_i=i\Delta x } . Depois de discretizar o espaço e o tempo, as derivadas contínuas são aproximadas por diferenças finitas. Isso envolve substituir as derivadas por aproximações baseadas nos valores de uma função nos pontos discretos:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial u}{\partial t} \approx \frac{u_i^{n+1} - u_i^n}{\Delta t}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^2 u}{\partial t^2} \approx \frac{u_i^{n+1} - 2u_i^n + u_i^{n-1}}{(\Delta t)^2} } para o tempo.

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial u}{\partial x} \approx \frac{u_{i+1}^n - u_i^n}{\Delta x} e \frac{\partial^2 u}{\partial x^2} \approx \frac{u_{i+1}^n - 2u_i^n + u_{i-1}^n}{(\Delta x)^2} } para o espaço.

Na equação de Klein-Gordon, escrevemos desta o método das diferenças finitas:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^2 \psi(x,t)}{\partial t^2} \approx \frac{\psi(x,t+\Delta t) - 2\psi(x,t) + \psi(x,t-\Delta t)}{(\Delta t)^2}}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^2 \psi(x,t)}{\partial x^2} \approx \frac{\psi(x+\Delta x,t) - 2\psi(x,t) + \psi(x- \Delta x,t)}{(\Delta x)^2} }

ou seja:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\psi(x,t+\Delta t) - 2\psi(x,t) + \psi(x,t-\Delta t)}{(\Delta t)^2} = c^2 \frac{\psi(x+\Delta x,t) - 2\psi(x,t) + \psi(x,t-\Delta t)}{(\Delta x)^2} - \frac{m^2 c^4}{\hbar^2} \psi }

isso nos leva a equação final:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x,t+\Delta t) - 2\psi(x,t) + \psi(x,t-\Delta t) =\frac{c^2 \Delta t^2}{\Delta x^2} \psi(x+\Delta x,t) - 2\psi(x,t) + \psi(x,t-\Delta,t) - \frac{m^2 c^4 \Delta t^2}{\hbar^2} \psi }

chamarei Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha = \frac{c \Delta t}{\Delta x} } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = \frac{m c^2 \Delta t}{\hbar} }

portanto, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x,t+\Delta t) - 2\psi(x,t) + \psi(x,t-\Delta t) =\alpha^2 \psi(x+\Delta x,t) - 2\psi(x,t) + \psi(x,t-\Delta t) - \beta^2 \psi }

ou, mais usualmente: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_i^{n+1} = 2\psi_i^n - \psi_i^{n-1} + \alpha^2 ( \psi_{i+1}^n - 2\psi_i^n + \psi_{i-1}^n) - \beta^2 \psi }

CRITÉRIO DE ESTABILIDADE

Forma Contínua e Discretização: A equação de Klein-Gordon contínua é: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^2 \psi}{\partial t^2} = c^2 \frac{\partial^2 \psi}{\partial x^2} - \frac{m^2 c^4}{\hbar^2} \psi. }

A forma discreta, usando diferenças finitas centralizadas no tempo e no espaço, é: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_i^{n+1} = 2 \psi_i^n - \psi_i^{n-1} + \frac{c^2 \Delta t^2}{\Delta x^2} (\psi_{i+1}^n - 2 \psi_i^n + \psi_{i-1}^n) - \frac{m^2 c^4 \Delta t^2}{\hbar^2} \psi_i^n. } Aqui, definimos os coeficientes: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha = \frac{c \Delta t}{\Delta x}, \quad \beta = \frac{m c^2 \Delta t}{\hbar}. }

Suposição de Solução Harmônica: Substituímos uma solução da forma: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_i^n = G^n e^{i k x_i}, } onde:

na equação: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^{n+1} e^{i k x_i} = 2 G^n e^{i k x_i} - G^{n-1} e^{i k x_i} + \alpha^2 G^n \left(e^{i k x_{i+1}} - 2 e^{i k x_i} + e^{i k x_{i-1}}\right) - \beta^2 G^n e^{i k x_i}. }

Simplificação:

Como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i k x_{i+1}} = e^{i k x_i} e^{i k \Delta x} } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i k x_{i-1}} = e^{i k x_i} e^{-i k \Delta x} } , o termo centralizado se torna: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i k x_{i+1}} - 2 e^{i k x_i} + e^{i k x_{i-1}} = e^{i k x_i} \left(e^{i k \Delta x} - 2 + e^{-i k \Delta x}\right). } Usando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i k \Delta x} + e^{-i k \Delta x} = 2 \cos(k \Delta x) } , temos: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i k x_{i+1}} - 2 e^{i k x_i} + e^{i k x_{i-1}} = e^{i k x_i} \left(-2 + 2 \cos(k \Delta x)\right). } Substituímos isso na equação e cancelamos o fator Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i k x_i} } , que nunca é zero: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^{n+1} = 2 G^n - G^{n-1} - \alpha^2 (2 - 2 \cos(k \Delta x)) G^n - \beta^2 G^n. }

Simplificando mais, obtemos: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^{n+1} = (2 - \alpha^2 (2 - 2 \cos(k \Delta x)) - \beta^2) G^n - G^{n-1}. }

Equação Característica: Assumimos uma solução na forma de uma equação quadrática Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle G } : Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^2 - G \left(2 - \alpha^2 (2 - 2 \cos(k \Delta x)) - \beta^2 \right) + 1 = 0. }

Condição de Estabilidade: Para estabilidade, as raízes de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle G } devem satisfazer Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle |G| \leq 1 } . Isso leva ao critério: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha \leq 1, \quad \text{ou seja,} \quad \frac{c \Delta t}{\Delta x} \leq 1. }

Conclusão Matemática: A condição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha \leq 1 } garante que os termos oscilatórios na solução não crescem exponencialmente. Essa análise também mostra que:

Quanto menor o passo de tempo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta t } , mais precisa e estável é a solução. A relação entre os passos de tempo e espaço é crucial: aumentar muito Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta t } sem ajustar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x } pode levar à instabilidade.

C.C e C.I

Condições iniciais e condições de contorno são fundamentais para a resolução da equação, já que elas ditam o comportamento da função oa longo do tempo e ao longo do espaço, para plotar a evolução temporal, utilizarei as seguintes condições iniciais e de contorno:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x,0) = Ae^{-\frac{x-x_0}{2\sigma^2}}} que define um pulso gaussiano como condição inicial.

e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial \psi(x,0)}{\partial t} =0 } que define que, no instante de tempo t=0, a função não possui velocidade inicial, o que implica que o pulso está parado inicialmente e sua evolução se deve pela propagação de flutuações espaciais.

Nesta condição, A é a altura do pulso, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0 } é a posição central do pulso e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma } é a largura do pulso.

Utilizarei também as condições de contorno em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(0,t)= 0 } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(L,t)=0 } o que garante que a função 'morra' nas pontas.

Utilizando estas condições iniciais e condições de contorno, foi feito um gif que mostra a evolução temporal da equação de Klein-Gordon utilizando o método das diferenças finitas:

Estatico.png

Klein 2.gif

Estabilidade.gif


Localização Inicial: No gráfico mostrado, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x,t) } tem um pico bem definido, o que sugere que a partícula está localizada inicialmente em torno de um ponto central no espaço. Isso significa que a probabilidade da partícula estar presente é maior nessa região (em torno do pico), e diminui nas bordas. No gráfico mostrado acima, tem um pico bem definido, o que sugere que a partícula está localizada inicialmente em torno de um ponto central no espaço. Isso significa que a probabilidade da partícula estar presente é maior nessa região (em torno do pico), e diminui nas bordas.


Código utilizado

import numpy as np

import matplotlib.pyplot as plt

from matplotlib.animation import FuncAnimation


L = 10.0 # Comprimento da simulação

Nx = 100 # Número de pontos espaciais

dx = L / Nx # Passo espacial

T_max = 30 # Tempo máximo de simulação

m = 1.0 # Massa da partícula

c = 1.0 # Velocidade da luz

hbar = 1.0 # Constante de Planck reduzida


A = 1.0 # Amplitude do pulso

x0 = L / 2 # Posição central do pulso

sigma = 0.5 # Largura do pulso


x = np.linspace(0, L, Nx)


phi_0 = A * np.exp(-((x - x0)**2) / (2 * sigma**2))

dphi_0 = np.zeros(Nx) # Derivada inicial nula

  1. estabilidade

alpha_stable = 0.5 # Valor estável para alpha (c * dt / dx)

dt_stable = alpha_stable * dx / c

alpha_unstable = 1.5 # Valor instável para alpha (c * dt / dx)

dt_unstable = alpha_unstable * dx / c


Nt_stable = int(T_max / dt_stable)

Nt_unstable = int(T_max / dt_unstable)


def evolve_wave(dt, Nt): 

   phi = np.zeros((Nt, Nx))

   phi[0, :] = phi_0

   phi[1, :] = phi_0 + dt * dphi_0



   for n in range(1, Nt-1):

       for i in range(1, Nx-1):

           phi[n+1, i] = 2 * phi[n, i] - phi[n-1, i] + (dt**2) * (

               (phi[n, i+1] - 2 * phi[n, i] + phi[n, i-1]) / dx**2 

               - (m**2 * c**2 / hbar**2) * phi[n, i]
           )

   return phi


phi_stable = evolve_wave(dt_stable, Nt_stable)

phi_unstable = evolve_wave(dt_unstable, Nt_unstable)


fig, ax = plt.subplots(2, 1, figsize=(10, 8))


def update_stable(frame): 

   ax[0].cla()

   ax[0].plot(x, phi_stable[frame, :], label=f'Tempo: {frame * dt_stable:.2f}s')

   ax[0].set_title("Evolução Estável")

   ax[0].set_xlim(0, L)

   ax[0].set_ylim(-1.5, 1.5)

   ax[0].legend()


def update_unstable(frame): 

   ax[1].cla()

   ax[1].plot(x, phi_unstable[frame, :], label=f'Tempo: {frame * dt_unstable:.2f}s')

   ax[1].set_title("Evolução Instável")

   ax[1].set_xlim(0, L)

   ax[1].set_ylim(-1.5, 1.5)

   ax[1].legend()


def init(): 

   for a in ax:

       a.clear()

   return ax
  1. Atualização combinada para animação

def update(frame): 

   update_stable(frame)

   update_unstable(frame)

   return ax
  1. Criando a animação

frames_stable = range(0, Nt_stable, max(1, Nt_stable // 150))

frames_unstable = range(0, Nt_unstable, max(1, Nt_unstable // 150))

ani = FuncAnimation(fig, update, frames=min(len(frames_stable), len(frames_unstable)),

init_func=init, blit=False)


  1. Salvando as animações

fig.tight_layout()

ani.save('klein_gordon_stable_vs_unstable.gif', writer='pillow', fps=30)

plt.show()

Disponível em “http://fiscomp.if.ufrgs.br/index.php?title=Equação_de_Klein-Gordon&oldid=11403”