Termostato de Andersen: mudanças entre as edições
Sem resumo de edição |
|||
| (67 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
== INTRODUÇÃO == | == INTRODUÇÃO == | ||
A dinâmica molecular é uma técnica que naturalmente simula sistemas clássicos compostos por N partículas interagindo dentro de um volume V. Nesse contexto, as posições das partículas são atualizadas com base no potencial de interação escolhido. Sob a suposição de ergodicidade — ou seja, que as médias temporais equivalem às médias de ensemble —, as simulações resultam em amostragens do ensemble microcanônico (NVE). Nesse ensemble, o número de partículas N, o volume V, e a energia total E permanecem constantes (aproximadamente). | A dinâmica molecular é uma técnica que naturalmente<ref name="frenkel">Frenkel, D., & Smit, B. (2002). Understanding molecular simulation: From algorithms to applications (2nd ed.). Academic Press.</ref> simula sistemas clássicos compostos por N partículas interagindo dentro de um volume V. Nesse contexto, as posições das partículas são atualizadas com base no potencial de interação escolhido. Sob a suposição de ergodicidade — ou seja, que as médias temporais equivalem às médias de ensemble —, as simulações resultam em amostragens do ensemble microcanônico (NVE). Nesse ensemble, o número de partículas N, o volume V, e a energia total E permanecem constantes (aproximadamente). | ||
Ao colocar um sistema em contato com um reservatório térmico a uma temperatura T, mudamos do ensemble microcanônico (NVE), onde a energia é mantida constante, para o ensemble canônico (NVT), no qual a temperatura do sistema é constante. Nesse novo ensemble, a distribuição de probabilidade das velocidades das partículas segue a forma da distribuição de Maxwell-Boltzmann, uma distribuição gaussiana associada à temperatura T. Um dos métodos mais simples para realizar uma amostragem correta do ensemble canônico é o termostato de Andersen. Neste estudo, focaremos na análise desse termostato, explorando sua implementação, características e aplicação na simulação de sistemas termodinâmicos. | Ao colocar um sistema em contato com um reservatório térmico a uma temperatura T, mudamos do ensemble microcanônico (NVE), onde a energia é mantida constante, para o ensemble canônico (NVT), no qual a temperatura do sistema é constante. Nesse novo ensemble, a distribuição de probabilidade das velocidades das partículas segue a forma da distribuição de Maxwell-Boltzmann, uma distribuição gaussiana associada à temperatura T. Um dos métodos mais simples para realizar uma amostragem correta do ensemble canônico é o termostato de Andersen. Neste estudo, focaremos na análise desse termostato, explorando sua implementação, características e aplicação na simulação de sistemas termodinâmicos. | ||
== FUNDAMENTO TEÓRICO == | == FUNDAMENTO TEÓRICO E DETALHES DA IMPLEMENTAÇÃO == | ||
=== Condições de Contorno Periódicas === | |||
As condições de contorno periódicas são fundamentais para garantir que simulações computacionais de sistemas físicos representem com precisão o comportamento de sistemas grandes e infinitos. Elas ajudam a evitar efeitos de borda que não são representativos do comportamento real de partículas em um espaço muito grande, permitindo simulações mais realistas e precisas. | |||
É utilizada a convenção da imagem mínima, que calcula a menor distância entre as partículas, sendo essa sempre menor ou igual a <math>L/2</math>. | |||
=== Integração de Velocity-Verlet === | |||
Escolhida principalmente por não ser de <math>O(N^2)</math> como o RK2<ref name="frenkel">Frenkel, D., & Smit, B. (2002). Understanding molecular simulation: From algorithms to applications (2nd ed.). Academic Press.</ref>, por exemplo. Precisamos calcular apenas 1 vez a força em cada passo do algoritmo. Assim, é o melhor "custo-benefício" dentre os possíveis algoritmos, possibilitando precisão suficiente. | |||
=== Condições Iniciais === | |||
Em todas as simulações, as partículas foram inicialmente posicionadas em uma grade cúbica uniformemente espaçada. Essa abordagem foi adotada para evitar que as partículas começassem muito próximas umas das outras, o que poderia gerar erros devido ao rápido aumento do potencial de Lennard-Jones quando as partículas estão muito próximas. | |||
As velocidades foram escolhidas a partir de uma distribuição uniforme no intervalo <math>[-0.5,0.5]</math>, sendo reescaladas para a temperatura desejada<ref name="frenkel">Frenkel, D., & Smit, B. (2002). Understanding molecular simulation: From algorithms to applications (2nd ed.). Academic Press.</ref>. | |||
=== Potencial de Lennard-Jones === | |||
O potencial de Lennard-Jones é amplamente utilizado para descrever as interações entre partículas em simulações de dinâmica molecular. Ele captura de forma simples e eficiente o comportamento atrativo de longo alcance e o repulsivo de curto alcance, que são características comuns em sistemas interatômicos e intermoleculares. | |||
Matematicamente, o potencial de Lennard-Jones é dado por: | |||
<math>U(r) = 4 \varepsilon \left[ \left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^6 \right]</math> | |||
onde: | |||
* <math>r</math> é a distância entre dois centros de partículas, | |||
* <math>\varepsilon</math> é a profundidade do poço de potencial, representando a intensidade da interação atrativa, | |||
* <math>\sigma</math> é a distância na qual o potencial é igual a zero. | |||
Nas simulações deste estudo foi utilizado o potencial de Lennard-Jones truncado para otimização, onde <math>r_c = 2.5\sigma</math> foi escolhido como o raio de corte, a partir do qual o potencial é considerado zero. Além disso, para evitar descontinuidades, o potencial também é deslocado, temos então: | |||
<math> | |||
U_{\text{truncado e deslocado}}(r) = | |||
\begin{cases} | |||
4\varepsilon \left[ \left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^6 \right] - U(r_c), & \text{se } r \leq r_c, \\ | |||
0, & \text{se } r > r_c. | |||
\end{cases} | |||
</math> | |||
=== Unidades Adimensionais === | |||
Para simplificar e possibilitar a comparação entre diferentes sistemas, todas as grandezas foram convertidas para unidades adimensionais, normalizando com base na massa e nos parâmetros do potencial: | |||
*<math>m</math> | |||
*<math>\sigma</math> | |||
*<math>\epsilon</math> | |||
Para facilitar os cálculos, em todas as simulações foram adotados <math>m=1</math>, <math>\sigma=1</math> e <math>\epsilon=1</math>. | |||
=== Distribuição de Maxwell-Boltzmann === | |||
A distribuição de Maxwell-Boltzmann descreve como as velocidades das partículas em um sistema no ensemble canônico estão distribuídas em equilíbrio térmico. | |||
Para um sistema de partículas com temperatura <math>T</math>, a função de distribuição de Maxwell-Boltzmann <math>f(v)</math> para a velocidade <math>v</math> de uma partícula é dada pela seguinte equação: | |||
<math>f(v) = 4 \pi \left(\frac{m}{2 \pi k_B T} \right)^{3/2} v^2 e^{-\frac{m v^2}{2 k_B T}}</math> | |||
=== Temperatura === | === Temperatura === | ||
<math> \left\langle \frac{1}{2} | A definição de temperatura em um sistema clássico em função das velocidades das partículas pode ser obtida pela equipartição de energia: | ||
<math>\ | |||
<math> \left\langle \frac{1}{2} m v_\alpha^2 \right\rangle = \frac{1}{2} k_B T </math> | |||
Temos então: | |||
<math>T(t) = \frac{1}{k_B N_f} \sum_{i=1}^{N_f} m_i v_i^2</math> | |||
onde <math>N_f</math> é o número de graus de liberdade do sistema. No ensemble microcanônico, como o momento é conservado, temos <math>N_f=3N-3</math>, mas no ensemble canônico, e portanto no termostato de Andersen, o momento não é conservado e utilizamos <math>N_f=3N</math>. | |||
== TERMOSTATO DE ANDERSEN == | == TERMOSTATO DE ANDERSEN == | ||
Para simular o contato do sistema com um reservatório térmico, a cada passo de tempo Δt é realizado um procedimento de Monte Carlo. Nesse processo, N | Para simular o contato do sistema com um reservatório térmico, a cada passo de tempo Δt é realizado um procedimento de Monte Carlo<ref name="stochastic">Li, D., Chen, Z., Zhang, Z., & Liu, J. (2017). Understanding molecular dynamics with stochastic processes via real or virtual dynamics. Chinese Journal of Chemical Physics, 30(6), 735–760. https://doi.org/10.1063/1674-0068/30/cjcp1711223</ref>. Nesse processo, algumas partículas (nesse estudo foi escolhido <math>N</math>, ou seja, cada partícula é, em media, sorteada uma vez a cada passo) são selecionadas aleatoriamente, uma de cada vez, e suas velocidades são atualizadas. Essas novas velocidades são sorteadas a partir da distribuição gaussiana centrada em zero com <math>\sigma = \sqrt{T}</math>. Essa abordagem introduz um elemento de estocasticidade ao modelo, permitindo que a temperatura média do sistema flutue em torno da temperatura T do reservatório. | ||
Na prática, a interação entre o sistema e o reservatório é controlada pela frequência de colisão <math>\nu</math>. Para cada partícula, é gerado um número aleatório <math>r</math> no intervalo [0,1]. Caso <math>r<\nu * \Delta t </math> a velocidade da partícula é atualizada conforme descrito. | Na prática, a interação entre o sistema e o reservatório é controlada pela frequência de colisão <math>\nu</math>. Para cada partícula, é gerado um número aleatório <math>r</math> no intervalo [0,1]. Caso <math>r<\nu * \Delta t </math> a velocidade da partícula é atualizada conforme descrito. | ||
| Linha 30: | Linha 93: | ||
== RESULTADOS == | == RESULTADOS == | ||
Para a análise, foram escolhidas 3 temperaturas diferentes. Para cada uma delas, foi simulado <math>N = 108</math> partículas, com densidade <math>p=0.8442</math>, <math>\nu =0.5</math>, <math>\Delta t =0.001</math> e número de passos <math>n=50.000</math>. | |||
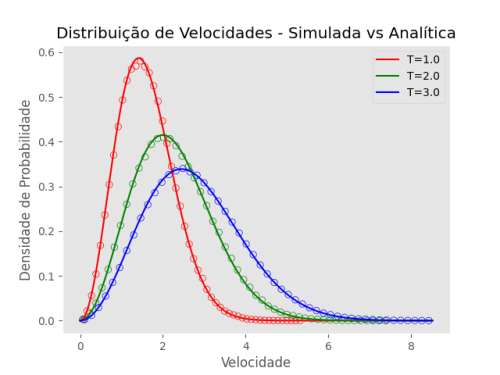
Para checar de forma mais consistente se o sistema no equilíbrio realmente corresponde ao ensemble canônico, foi comparada a curva teórica da distribuição de Maxwell-Boltzmann para a temperatura correspondente, com um histograma das velocidades em todas as dimensões obtidas nos últimos 40.000 passos (os primeiros 10.000 passos são o transiente para o equilíbrio). | |||
Na figura abaixo, vemos que houve uma aproximação muito boa da distribuição de velocidades da simulação com os valores esperados pela distribuição de Maxwell-Boltzmann. | |||
[[Arquivo:Velocity_distribution_1.0_2.0_3.0.png|500px|center|thumb|Figura 1: Comparação da distribuição de Maxwell-Boltzmann (linha sólida) com a distribuição de velocidades obtida nos últimos 40.000 passos da simulação (círculos) para diferentes temperaturas.]] | |||
Além disso, são mostradas abaixo a série temporal para cada uma das temperaturas, com a média e desvio padrão da temperatura dos últimos <math>40.000</math> passos. | |||
=== T=1 === | |||
<math>\mu = 1.011</math> | <math>\mu = 1.011</math> | ||
<math>\sigma = 0.067</math> | <math>\sigma = 0.067</math> | ||
[[Arquivo:Temp_1.0_totalsteps_50000_nu_0.5.png| | [[Arquivo:Temp_1.0_totalsteps_50000_nu_0.5.png|500px|center|thumb|Figura 1: Evolução da temperatura durante a simulação com temperatura do reservatório <math>T=1</math>.]] | ||
=== T=2 === | |||
<math>\mu = 2.025</math> | <math>\mu = 2.025</math> | ||
<math>\sigma = 0.166</math> | <math>\sigma = 0.166</math> | ||
[[Arquivo:Temp_2.0_totalsteps_50000_nu_0.5.png| | [[Arquivo:Temp_2.0_totalsteps_50000_nu_0.5.png|500px|center|thumb|Figura 3: Evolução da temperatura durante a simulação com temperatura do reservatório <math>T=2</math>.]] | ||
=== T=3 === | |||
<math>\mu = 3.027</math> | <math>\mu = 3.027</math> | ||
<math>\sigma = 0.247</math> | <math>\sigma = 0.247</math> | ||
[[Arquivo:Temp_3.0_totalsteps_50000_nu_0.5.png| | [[Arquivo:Temp_3.0_totalsteps_50000_nu_0.5.png|500px|center|thumb|Figura 5: Evolução da temperatura durante a simulação com temperatura do reservatório <math>T=3</math>.]] | ||
=== Análise do parâmetro da frequência de colisão === | |||
A frequência de colisão <math>\nu</math> controla o nível de interação entre o sistema e o reservatório térmico. Quando <math>\nu</math> é muito baixa, o número de colisões entre o sistema e o reservatório em um intervalo de tempo é pequeno, exigindo um tempo maior de simulação para equilibrar a temperatura. Nesse caso, o sistema permanece por períodos mais longos em estados que não refletem o equilíbrio térmico desejado, o que prejudica a convergência para o ensemble canônico. | |||
Na figura abaixo vemos que a flutuação parece estar se aproximando lentamente de <math>T=1.0</math>, com mais tempo de simulação parece que essa temperatura será alcançada. | |||
[[Arquivo:Temp 1.0 totalsteps 100000 nu 0.01.png|500px|center|thumb|Figura 6: Evolução temporal da temperatura para <math>\nu=0.01</math> e <math>T=1</math>.]] | |||
Por outro lado, valores muito altos de <math>\nu</math> podem introduzir um excesso de estocasticidade no modelo, fazendo com que a interação entre as partículas percam importância. Esse regime pode ser indesejado em simulações onde as interações interpartículas são críticas para o comportamento do sistema. Além disso, o termostato de Andersen introduz descontinuidades nas velocidades e, por consequência, no momento, sendo assim, não é possível medir propriedades de transporte, como difusão e viscosidade. | |||
Na figura abaixo é visto claramente que a convergência demorou mais passos do que no caso de <math>\nu=0.5</math>. | |||
[[Arquivo:Temp 1.0 totalsteps 50000 nu 0.1.png|500px|center|thumb|Figura 6: Evolução temporal da temperatura para <math>\nu=0.1</math> e <math>T=1</math>.]] | |||
== CONCLUSÃO == | |||
Este estudo implementou e analisou o termostato de Andersen como ferramenta para simular sistemas no ensemble canônico (NVT). A estocasticidade introduzida pela atualização aleatória das velocidades das partículas, baseada na distribuição de Maxwell-Boltzmann, mostrou-se eficiente para reproduzir a temperatura do reservatório térmico e as propriedades estatísticas de equilíbrio termodinâmico. Os resultados demonstraram a acurácia do método. A precisão diminui com o aumento da temperatura, como esperado para essa distribuição<ref name="frenkel">Frenkel, D., & Smit, B. (2002). Understanding molecular simulation: From algorithms to applications (2nd ed.). Academic Press.</ref>. | |||
No entanto, foi observado um aumento das flutuações em temperaturas mais altas, como evidenciado pelos desvios padrão maiores. Isso é consistente com o comportamento esperado para sistemas térmicos e reflete o impacto da energia térmica sobre as velocidades das partículas. | |||
Ao longo das simulações realizadas, foi necessário utilizar um valor de frequência de colisão <math>\nu = 0.5</math>. Para valores menores de <math>\nu</math>, observou-se que o sistema não convergia adequadamente para a temperatura do reservatório térmico, apresentando desvios significativos em relação ao valor esperado. Esse comportamento pode ser explicado pelo <math>\Delta t</math> escolhido. Se fosse menor, apesar de as colisões demorarem mais para acontecer, a dinâmica também seria mais lenta, e talvez o valor de <math>\nu</math> pudesse ser menor. | |||
Em suma, o termostato de Andersen se mostrou uma ferramenta valiosa e relativamente simples para a simulação de sistemas interagindo com um reservatório térmico. A abordagem permite a obtenção de propriedades relevantes no ensemble canônico e abre caminho para estudos mais aprofundados, como medições de outras propriedades termodinâmicas, a comparação com outros termostatos ou a aplicação a sistemas mais complexos. | |||
[https://github.com/gabriel-englert/Andersen-Thermostat código utilizado] | |||
=== REFERÊNCIAS === | |||
<references /> | |||
Edição atual tal como às 14h39min de 11 de dezembro de 2024
INTRODUÇÃO
A dinâmica molecular é uma técnica que naturalmente[1] simula sistemas clássicos compostos por N partículas interagindo dentro de um volume V. Nesse contexto, as posições das partículas são atualizadas com base no potencial de interação escolhido. Sob a suposição de ergodicidade — ou seja, que as médias temporais equivalem às médias de ensemble —, as simulações resultam em amostragens do ensemble microcanônico (NVE). Nesse ensemble, o número de partículas N, o volume V, e a energia total E permanecem constantes (aproximadamente).
Ao colocar um sistema em contato com um reservatório térmico a uma temperatura T, mudamos do ensemble microcanônico (NVE), onde a energia é mantida constante, para o ensemble canônico (NVT), no qual a temperatura do sistema é constante. Nesse novo ensemble, a distribuição de probabilidade das velocidades das partículas segue a forma da distribuição de Maxwell-Boltzmann, uma distribuição gaussiana associada à temperatura T. Um dos métodos mais simples para realizar uma amostragem correta do ensemble canônico é o termostato de Andersen. Neste estudo, focaremos na análise desse termostato, explorando sua implementação, características e aplicação na simulação de sistemas termodinâmicos.
FUNDAMENTO TEÓRICO E DETALHES DA IMPLEMENTAÇÃO
Condições de Contorno Periódicas
As condições de contorno periódicas são fundamentais para garantir que simulações computacionais de sistemas físicos representem com precisão o comportamento de sistemas grandes e infinitos. Elas ajudam a evitar efeitos de borda que não são representativos do comportamento real de partículas em um espaço muito grande, permitindo simulações mais realistas e precisas.
É utilizada a convenção da imagem mínima, que calcula a menor distância entre as partículas, sendo essa sempre menor ou igual a .
Integração de Velocity-Verlet
Escolhida principalmente por não ser de como o RK2[1], por exemplo. Precisamos calcular apenas 1 vez a força em cada passo do algoritmo. Assim, é o melhor "custo-benefício" dentre os possíveis algoritmos, possibilitando precisão suficiente.
Condições Iniciais
Em todas as simulações, as partículas foram inicialmente posicionadas em uma grade cúbica uniformemente espaçada. Essa abordagem foi adotada para evitar que as partículas começassem muito próximas umas das outras, o que poderia gerar erros devido ao rápido aumento do potencial de Lennard-Jones quando as partículas estão muito próximas.
As velocidades foram escolhidas a partir de uma distribuição uniforme no intervalo , sendo reescaladas para a temperatura desejada[1].
Potencial de Lennard-Jones
O potencial de Lennard-Jones é amplamente utilizado para descrever as interações entre partículas em simulações de dinâmica molecular. Ele captura de forma simples e eficiente o comportamento atrativo de longo alcance e o repulsivo de curto alcance, que são características comuns em sistemas interatômicos e intermoleculares.
Matematicamente, o potencial de Lennard-Jones é dado por:
onde:
- é a distância entre dois centros de partículas,
- é a profundidade do poço de potencial, representando a intensidade da interação atrativa,
- é a distância na qual o potencial é igual a zero.
Nas simulações deste estudo foi utilizado o potencial de Lennard-Jones truncado para otimização, onde foi escolhido como o raio de corte, a partir do qual o potencial é considerado zero. Além disso, para evitar descontinuidades, o potencial também é deslocado, temos então:
Unidades Adimensionais
Para simplificar e possibilitar a comparação entre diferentes sistemas, todas as grandezas foram convertidas para unidades adimensionais, normalizando com base na massa e nos parâmetros do potencial:
Para facilitar os cálculos, em todas as simulações foram adotados , e .
Distribuição de Maxwell-Boltzmann
A distribuição de Maxwell-Boltzmann descreve como as velocidades das partículas em um sistema no ensemble canônico estão distribuídas em equilíbrio térmico. Para um sistema de partículas com temperatura , a função de distribuição de Maxwell-Boltzmann para a velocidade de uma partícula é dada pela seguinte equação:
Temperatura
A definição de temperatura em um sistema clássico em função das velocidades das partículas pode ser obtida pela equipartição de energia:
Temos então:
onde é o número de graus de liberdade do sistema. No ensemble microcanônico, como o momento é conservado, temos , mas no ensemble canônico, e portanto no termostato de Andersen, o momento não é conservado e utilizamos .
TERMOSTATO DE ANDERSEN
Para simular o contato do sistema com um reservatório térmico, a cada passo de tempo Δt é realizado um procedimento de Monte Carlo[2]. Nesse processo, algumas partículas (nesse estudo foi escolhido , ou seja, cada partícula é, em media, sorteada uma vez a cada passo) são selecionadas aleatoriamente, uma de cada vez, e suas velocidades são atualizadas. Essas novas velocidades são sorteadas a partir da distribuição gaussiana centrada em zero com . Essa abordagem introduz um elemento de estocasticidade ao modelo, permitindo que a temperatura média do sistema flutue em torno da temperatura T do reservatório.
Na prática, a interação entre o sistema e o reservatório é controlada pela frequência de colisão . Para cada partícula, é gerado um número aleatório no intervalo [0,1]. Caso a velocidade da partícula é atualizada conforme descrito.
Algoritmo
Podemos descrever o algoritmo em 4 passos:
1. Inicia-se com um conjunto de posições e velocidades.
2. Integra-se as equações do movimento para um passo .
3. N partículas são selecionadas para colidir com o reservatório térmico.
4. Para cada partícula selecionada, definir nova velocidade a partir da distribuição de Maxwell-Boltzmann correspondente à temperatura T do reservatório.
RESULTADOS
Para a análise, foram escolhidas 3 temperaturas diferentes. Para cada uma delas, foi simulado partículas, com densidade , , e número de passos . Para checar de forma mais consistente se o sistema no equilíbrio realmente corresponde ao ensemble canônico, foi comparada a curva teórica da distribuição de Maxwell-Boltzmann para a temperatura correspondente, com um histograma das velocidades em todas as dimensões obtidas nos últimos 40.000 passos (os primeiros 10.000 passos são o transiente para o equilíbrio). Na figura abaixo, vemos que houve uma aproximação muito boa da distribuição de velocidades da simulação com os valores esperados pela distribuição de Maxwell-Boltzmann.
Além disso, são mostradas abaixo a série temporal para cada uma das temperaturas, com a média e desvio padrão da temperatura dos últimos passos.
T=1
T=2
T=3
Análise do parâmetro da frequência de colisão
A frequência de colisão controla o nível de interação entre o sistema e o reservatório térmico. Quando é muito baixa, o número de colisões entre o sistema e o reservatório em um intervalo de tempo é pequeno, exigindo um tempo maior de simulação para equilibrar a temperatura. Nesse caso, o sistema permanece por períodos mais longos em estados que não refletem o equilíbrio térmico desejado, o que prejudica a convergência para o ensemble canônico. Na figura abaixo vemos que a flutuação parece estar se aproximando lentamente de , com mais tempo de simulação parece que essa temperatura será alcançada.
Por outro lado, valores muito altos de podem introduzir um excesso de estocasticidade no modelo, fazendo com que a interação entre as partículas percam importância. Esse regime pode ser indesejado em simulações onde as interações interpartículas são críticas para o comportamento do sistema. Além disso, o termostato de Andersen introduz descontinuidades nas velocidades e, por consequência, no momento, sendo assim, não é possível medir propriedades de transporte, como difusão e viscosidade.
Na figura abaixo é visto claramente que a convergência demorou mais passos do que no caso de .
CONCLUSÃO
Este estudo implementou e analisou o termostato de Andersen como ferramenta para simular sistemas no ensemble canônico (NVT). A estocasticidade introduzida pela atualização aleatória das velocidades das partículas, baseada na distribuição de Maxwell-Boltzmann, mostrou-se eficiente para reproduzir a temperatura do reservatório térmico e as propriedades estatísticas de equilíbrio termodinâmico. Os resultados demonstraram a acurácia do método. A precisão diminui com o aumento da temperatura, como esperado para essa distribuição[1].
No entanto, foi observado um aumento das flutuações em temperaturas mais altas, como evidenciado pelos desvios padrão maiores. Isso é consistente com o comportamento esperado para sistemas térmicos e reflete o impacto da energia térmica sobre as velocidades das partículas.
Ao longo das simulações realizadas, foi necessário utilizar um valor de frequência de colisão . Para valores menores de , observou-se que o sistema não convergia adequadamente para a temperatura do reservatório térmico, apresentando desvios significativos em relação ao valor esperado. Esse comportamento pode ser explicado pelo escolhido. Se fosse menor, apesar de as colisões demorarem mais para acontecer, a dinâmica também seria mais lenta, e talvez o valor de pudesse ser menor.
Em suma, o termostato de Andersen se mostrou uma ferramenta valiosa e relativamente simples para a simulação de sistemas interagindo com um reservatório térmico. A abordagem permite a obtenção de propriedades relevantes no ensemble canônico e abre caminho para estudos mais aprofundados, como medições de outras propriedades termodinâmicas, a comparação com outros termostatos ou a aplicação a sistemas mais complexos.
REFERÊNCIAS
- ↑ 1,0 1,1 1,2 1,3 Frenkel, D., & Smit, B. (2002). Understanding molecular simulation: From algorithms to applications (2nd ed.). Academic Press.
- ↑ Li, D., Chen, Z., Zhang, Z., & Liu, J. (2017). Understanding molecular dynamics with stochastic processes via real or virtual dynamics. Chinese Journal of Chemical Physics, 30(6), 735–760. https://doi.org/10.1063/1674-0068/30/cjcp1711223


![{\displaystyle [-0.5,0.5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f82e0cb567f3dc7df3709b7077b346272589753)
![{\displaystyle U(r)=4\varepsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/374024e23ac5eb77e91b68ad9ba86ad3bbf5f113)




![{\displaystyle U_{\text{truncado e deslocado}}(r)={\begin{cases}4\varepsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]-U(r_{c}),&{\text{se }}r\leq r_{c},\\0,&{\text{se }}r>r_{c}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f31e7df3d28b3034f272e891cbe408afb986ae1)