Equação de Lotka-Volterra Competitiva Estocástica: mudanças entre as edições
Sem resumo de edição |
|||
| (58 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
== Introdução == | |||
== Equação de | As Equações de Lotka-Volterra fornecem um modelo para a previsão de sistemas biológicos considerando diversas relações entre populações. Exploraremos no vigente trabalho a relação de competitividade, juntamente da adição de um termo estocástico multiplicativo. Consideraremos duas e três populações, mostrando os gráficos de evolução temporal do número de indivíduos de cada espécie e os espaços de fase. Em todas as etapas serão mostrados os resultados considerando e desconsiderando o ruído para fins comparativos. Por fim, descreveremos o método de Fokker-Planck, utilizando um exemplo simples para a demonstração. | ||
== Equações para Duas Populações == | |||
Como uma primeira análise, considerando somente duas populações distintas, vamos explorar o modelo logístico, partindo das Equações de Lotka-Volterra, de duas espécies disputando um território, que pode ser descrito pelo seguinte par de relações: | |||
<center> | |||
<math> | |||
\frac{dx_1}{dt} = r_1x_1\left(1 - \frac{x_1 + \alpha_{12}x_2}{K_1}\right) | |||
</math> | |||
</center> | |||
<center> | |||
<math> | |||
\frac{dx_2}{dt} = r_2x_2\left(1 - \frac{x_2 + \alpha_{21}x_1}{K_2}\right) | |||
</math> | |||
</center> | |||
Nesse par, <math>x_1</math> e <math>x_2</math> representam as duas populações consideradas; <math>r_1</math> e <math>r_2</math> indicam o crescimento inerente per-capita, a capacidade de uma espécie em se reproduzir; <math>K_1</math> e <math>K_2</math> retratam a capacidade de carga, o número de indivíduos limite que o meio ambiente consegue suportar considerando o nicho ecológico ao que a espécie pertence; e <math>\alpha_{12}</math> e <math>\alpha_{21}</math>, o efeito que a espécie um tem na espécie dois e vice-versa. | |||
Para a adição de ruído ao sistema, vamos supor que o termo estocástico seja incorporado em cada equação de maneira a afetar somente a população <math> x_1 </math> ou a população <math> x_2 </math>, ou seja, estamos considerando que o ruído atinja cada população de maneira proporcional a sua quantidade de indivíduos em determinado período de tempo. Como um exemplo prático, podemos pensar no termo estocástico como a presença de um agente externo que infecte uma das populações isoladamente. Claro que o efeito resultante de existir uma doença se espalhando na espécie <math> x_1 </math> afeta o crescimento da espécie <math> x_2 </math>, entretanto esse efeito não é direto, sendo uma consequência da correlação entre o par de equações. | |||
Além disso, antes de de fato colocarmos o fator estocástico nas equações, precisamos de explicar qual o tipo de ruído a ser inserido. Para tanto, será introduzido o ruído branco, que é definido a partir de suas propriedades estatísticas que configuram sua média e sua função de correlação temporal, podendo ser expressas matematicamente por | |||
<center> | |||
<math> | |||
<\xi (t) > = 0 | |||
</math> | |||
</center> | |||
<center> | |||
<math> | |||
<\xi (t_1)\xi (t_2) > = \delta (t_2 - t_1) | |||
</math> | |||
</center> | |||
A primeira relação indica que o ruído branco possui média igual a zero, enquanto que a segunda indica o fato de os ruídos considerando diferentes tempos são independentes e, sendo assim, dá o nome branco ao ruído, pois a intensidade espectral de um processo estocástico é a Transformada de Fourier da função de correlação, sendo ela constante por se tratar de uma Delta de Dirac, logo todas as frequências estão presentes com mesma intensidade, com branco fazendo uma analogia a essa característica. | |||
Portanto, podemos reescrever as relações supracitadas considerando o ruído como | |||
<center> | |||
<math> | |||
\frac{dx_1}{dt} = r_1x_1\left(1 - \frac{x_1 + \alpha_{12}x_2}{K_1}\right) + x_1 \beta{_1} \xi{_1} (t) | |||
</math> | |||
</center> | |||
<center> | |||
<math> | |||
\frac{dx_2}{dt} = r_2x_2\left(1 - \frac{x_2 + \alpha_{21}x_1}{K_2}\right) + x_2 \beta{_2} \xi{_2} (t) | |||
</math> | |||
</center> | |||
com <math> \beta_1 </math> e <math> \beta_2 </math> sendo as amplitudes dos ruídos e <math> \xi_1 (t) </math> e <math> \xi_2 (t) </math> os ruídos brancos. | |||
=== Resolução Numérica pelo Método de Itô === | |||
Para então resolvermos as equações numericamente, vamos recorrer ao cálculo diferencial estocástico. Iniciamos, para esse fim, tomando a forma de Langevin | |||
<center> | |||
<math> | |||
dX = A(X(t), t)dt + B(X(t), t)\xi (t)dt | |||
</math> | |||
</center> | |||
Deveríamos, como próxima etapa, integrar ambos os lados da equação da seguinte forma | |||
<center> | |||
<math> | |||
\int_X^{X + \Delta X}dX' = \int_t^{t + \Delta t}A(X(t'), t')dt' + \int_t^{t + \Delta t}B(X(t'), t')\xi (t')dt' | |||
</math> | |||
</center> | |||
Como não podemos resolvê-la pelos métodos convencionais, pois <math> \xi (t) </math> torna a função não diferenciável apesar de ser contínua, utilizamos a relação | |||
<center> | |||
<math> | |||
B(X(t'),t') = B\left(\frac{X(t') + X(t' + \Delta t')}{2}, t'\right) | |||
</math> | |||
</center> | |||
Essa troca se justifica pelo fato de estarmos trocando o argumento de B pela média entre os valores de X no início e no fim do intervalo de integração, correspondendo a uma melhor estimação. Agora, tomando a integral, ficamos com a aproximação | |||
<center> | |||
<math> | |||
\Delta X(t) = A(X(t), t) \Delta t + B\left(X(t) + \frac{1}{2}\Delta X(t), t\right)\Delta W(t) | |||
</math> | |||
</center> | |||
Por seguinte, expandimos B em série de Taylor, excluímos o termo de ordem maior que dt e fazemos a substituição <math> \Delta t </math> por <math> \Delta W^2 </math> | |||
<center> | |||
<math> | |||
dX(t) = \underbrace{\left(A(X(t), t) + \frac{1}{2}\frac{\partial B}{\partial X}B(X(t), t)\right)}_{A^{(I)}(X(t), t)} dt + B(X(t), t)\bullet dW(t) | |||
</math> | |||
</center> | |||
Com isso, temos que a Equação diferencial de Itô é dada por | |||
<center> | |||
<math> | |||
dX(t) = A^{(I)}(X(t), t) dt + B(X(t), t) \bullet dW(t) | |||
</math> | |||
</center> | |||
Portanto, partindo da nossa relação para <math> x_1 </math> | |||
<center> | |||
<math> | |||
\frac{dx_1}{dt} = r_1x_1\left(1 - \frac{x_1 + \alpha_{12}x_2}{K_1}\right) + x_1 \beta{_1} \xi{_1} (t) | |||
</math> | |||
</center> | |||
Temos, isolando <math> dx_1 </math> | |||
<center> | |||
<math> | |||
dx_1 = r_1x_1\left(1 - \frac{x_1 + \alpha_{12}x_2}{K_1}\right) dt + x_1 \beta{_1} \underbrace{\xi{_1} (t) dt}_{dW} | |||
</math> | |||
</center> | |||
A partir disso, sabemos os coeficientes A(X(t),t) e B(X(t),t) de Langevin | |||
<center> | <center> | ||
<math> | <math> | ||
A(X_1(t),t) = r_1x_1\left(1 - \frac{x_1 + \alpha_{12}x_2}{K_1}\right) | |||
</math> | </math> | ||
</center> | </center> | ||
<center> | |||
<math> | |||
B(X_1(t),t) = x_1 \beta{_1} | |||
</math> | |||
</center> | |||
<center> | |||
<math> | |||
\frac{1}{2}\frac{\partial B}{\partial X_1}B(X_1(t), t) = \frac{1}{2}\beta_1^2x_1 | |||
</math> | |||
</center> | |||
Assim, substituindo os valores para encontrar a equação diferencial de Itô, obtemos | |||
<center> | <center> | ||
<math> | <math> | ||
dx_1 = r_1x_1\left(1 - \frac{x_1 + \alpha_{12}x_2}{K_1} + \frac{1}{2}\beta_1^2x_1\right) dt + x_1 \beta{_1} dW | |||
</math> | </math> | ||
</center> | </center> | ||
Analogamente, obtemos também a equação para a variável <math> x_2 </math> | |||
<center> | <center> | ||
<math> | <math> | ||
dx_2 = r_2x_2\left(1 - \frac{x_2 + \alpha_{21}x_1}{K_2} + \frac{1}{2}\beta_2^2x_2\right) dt + x_2 \beta{_2} dW | |||
</math> | </math> | ||
</center> | </center> | ||
=== Resultados === | |||
==== Caso Um ==== | |||
Com duas populações, vamos exemplificar nesta seção o caso em que a competitividade se dá de maneira igual, ou seja, todas as constantes possuem mesmo valor independentemente da população. A diferença, então, se dará a partir do ruído, que será maior para uma delas. | |||
Utilizando <math>r_1</math> = <math>r_2</math> = <math>\alpha_{12}</math> = <math>\alpha_{21}</math> = 1, <math>K_1</math> = <math>K_2</math> = 60 e população inicial de 10 indivíduos, a evolução temporal e o espaço de fases do sistema de duas populações podem ser vistos nas figuras abaixo. | |||
<center> | |||
[[Arquivo:Duas populacoes.png]] | |||
</center> | |||
<center> | |||
[[Arquivo:Duas populacoes fases.png]] | |||
</center> | |||
Podemos verificar que, a partir da adição de um ruído maior na população 2, a população 1 cedeu quando o tempo atingiu valor próximo a 30 unidades, comportamento este que não é visto no gráfico sem ruído, no qual as duas populações convivem de maneira igual e atingindo cada uma metade de sua população limite. Realizaram-se mais de 20 simulações e todas tiveram o mesmo efeito, com a população 2 prosperando em consequência do desaparecimento da população 1. | |||
==== Caso Dois ==== | |||
Agora, consideraremos uma pequena variação nas constantes de crescimento das populações, com um aumento de duas vezes para <math>r_1</math>. Todos os outros parâmetros são iguais ao Caso Um. Os resultados seguem nas figuras abaixo. | |||
<center> | |||
[[Arquivo:Duas populacoes r1 eh 2.png]] | |||
</center> | |||
<center> | |||
[[Arquivo:Duas populacoes r1 eh 2 fases.png]] | |||
</center> | |||
Mesmo com a população um possuindo taxa de crescimento duas vezes maior, a espécie com maior amplitude de ruído sobrevive ao final da simulação. | |||
== Equações para Três Populações == | == Equações para Três Populações == | ||
Os métodos de resolução numérica para três populações são completamente análogos aos métodos para duas populações; portanto, a matemática envolvida será omitida a partir de agora e somente serão discutidos os resultados. O conjunto de equações utilizado para três espécies distintas é | |||
<center> | <center> | ||
<math> | <math> | ||
\frac{dx_1}{dt} = r_1x_1\left(1 -\frac{x_1 + \alpha_{12}x_2 + \alpha_{13}x_3}{K_1} \right)</math> | \frac{dx_1}{dt} = r_1x_1\left(1 -\frac{x_1 + \alpha_{12}x_2 + \alpha_{13}x_3}{K_1} \right) + x_1 \beta{_1} \xi{_1} (t) | ||
</math> | |||
</center> | </center> | ||
<center> | <center> | ||
<math> | <math> | ||
\frac{dx_2}{dt} = r_2x_2\left(1 - \frac{x_2 + \alpha_{21}x_1 + \alpha_{23}x_3}{K_2}\right)</math> | \frac{dx_2}{dt} = r_2x_2\left(1 - \frac{x_2 + \alpha_{21}x_1 + \alpha_{23}x_3}{K_2}\right) + x_2 \beta{_2} \xi{_2} (t) | ||
</math> | |||
</center> | </center> | ||
<center> | <center> | ||
<math> | <math> | ||
\frac{dx_3}{dt} = r_3x_3\left(1 - \frac{x_3 + \alpha_{31}x_1 + \alpha_{32}x_2}{K_1}\right)</math> | \frac{dx_3}{dt} = r_3x_3\left(1 - \frac{x_3 + \alpha_{31}x_1 + \alpha_{32}x_2}{K_1}\right) + x_3 \beta{_3} \xi{_3} (t) | ||
</math> | |||
</center> | |||
=== Resultados === | |||
==== Caso Um ==== | |||
Como primeira análise, vamos ao caso análogo ao anterior de duas populações. Vamos considerar espécies semelhantes, trocando entre elas somente o fator de amplitude do ruído, com o maior fator sendo da população 2. Utilizamos <math>K_1</math> = <math>K_2</math> = <math>K_3</math> = 60, população inicial de 10 indivíduos e as outras constantes como um. As figuras a seguir mostram a evolução temporal e o espaço de fases do sistema. | |||
<center> | |||
[[Arquivo:Tres populacoes ctes iguais.png]] | |||
</center> | |||
<center> | |||
[[Arquivo:Tres populacoes ctes iguais fases.png]] | |||
</center> | |||
Podemos verificar que, assim como na seção anterior, a população com maior fator de ruído prosperou enquanto que as outras tiveram sua extinção em um tempo de 5 unidades. Quando desconsideramos o ruído, vemos que as três espécies convivem com mesmo comportamento populacional. | |||
==== Caso Dois ==== | |||
Para um segundo caso, vamos considerar os mesmos parâmetros de antes, modificando apenas os coeficientes entre as populações, dados na seguinte tabela. | |||
<center> | |||
{| class="wikitable" | |||
|+ Coeficientes <math>\alpha</math> | |||
|- | |||
! | |||
! <math>\alpha_{i1}</math> | |||
! <math>\alpha_{i2}</math> | |||
! <math>\alpha_{i3}</math> | |||
|- | |||
! <math>\alpha_{1j}</math> | |||
| 1 | |||
| 2 | |||
| 1 | |||
|- | |||
! <math>\alpha_{2j}</math> | |||
| 1 | |||
| 1 | |||
| 2 | |||
|- | |||
! <math>\alpha_{3j}</math> | |||
| 2 | |||
| 1 | |||
| 1 | |||
|} | |||
</center> | |||
Eles indicam que a população 1 tem dominância sobre a população 2, a população 2 tem dominância sobre a população 3 e a população 3 tem dominância sobre a população 1. As imagens podem ser vistas a seguir. | |||
<center> | |||
[[Arquivo:Tres populacoes 1 2 1 1 1 2 2 1 1.png]] | |||
</center> | |||
<center> | |||
[[Arquivo:Tres populacoes 1 2 1 1 1 2 2 1 1 fases.png]] | |||
</center> | </center> | ||
Vemos que, mesmo considerando as relações de dominância, a população com maior ruído sobressai no final, sendo a única espécie viva ao final da simulação. | |||
<br/> | |||
== Equações para | == Método de Fokker-Planck== | ||
A Equação de Fokker-Planck trata da equação diferencial da distribuição de probabilidade das variáveis de um sistema de Equações Diferenciais Estocásticas. Avaliaremos sua aplicação no sistema Lotka-Volterra competitivo para duas populações. | |||
Para um processo estocástico vetorial <math> X = [X_1, X_2, ... , X_n] </math>, a equação de Fokker-Planck tem a forma | |||
<center> | <center> | ||
<math> | <math> | ||
\frac{ | \frac{\partial P(x,t)}{\partial t} = \sum^n_{i=1} \frac{\partial[K_i(x,t)P(x,t)]}{\partial x_i} + \frac{1}{2} \sum^n_{i,j = 1}\frac{\partial^2[D_{ij}(x,t)P(x,t)]}{\partial x_i\partial x_j} | ||
</math> | </math> | ||
</center> | </center> | ||
em que | |||
< | <center> | ||
<math> | |||
K_i(x,t) = -A_i(x,t) | |||
</math> | |||
</center> | |||
e | |||
<center> | |||
<math> | |||
a = | D_{ij}(x,t) = \sum^m_{\alpha=1}B_{i,\alpha}(x,t)B_{j,\alpha}(x,t) | ||
</math> | |||
</center> | |||
Assim, para o nosso caso, temos | |||
<center> | |||
<math> | |||
\frac{\partial P(x_1,x_2,t)}{\partial t} = -\frac{\partial}{\partial x_1}\left[r_1x_1\left(1-\frac{x_1+\alpha_{12}x_2}{k_1}\right)P(x_1,x_2,t) \right] -\frac{\partial}{\partial x_2}\left[r_2x_2\left(1-\frac{x_2+\alpha_{21}x_1}{k_2}\right)P(x_1,x_2,t) \right] +\frac 12 \beta_1^2 \frac{\partial^2x_1^2P(x_1,x_2,t)}{\partial x_1^2} +\frac 12 \beta_2^2 \frac{\partial^2x_2^2P(x_1,x_2,t)}{\partial x_2^2} | |||
</math> | |||
</center> | |||
Resolvendo as derivadas por regra do produto e separando nas derivadas parciais de <math> P(x_1,x_2,t) </math> ficamos com | |||
<center> | |||
<math> | |||
\frac{\partial P(x_1,x_2,t)}{\partial t } = \delta_1 \frac{\partial^2 P}{\partial x_1^2} + \delta_2 \frac{\partial^2 P}{\partial x_2^2} + \gamma_1 \frac{\partial P}{\partial x_1} + \gamma_2 \frac{\partial P}{\partial x_2} + \omega P | |||
</math> | |||
</center> | |||
com | |||
<center> | |||
<math> | |||
\delta_1 = \frac{1}{2} \beta_1^2 x_1^2 | |||
</math> | |||
<math> | |||
\delta_2 = \frac{1}{2} \beta_2^2 x_2^2 | |||
</math> | |||
<math> | |||
\gamma_1 = \frac{r_1 x_1^2}{k_1} + \frac{r_1 x_1 \alpha_{12} x_2}{k_1} - r_1x_1 + 2\beta_1^2x_1 | |||
</math> | |||
<math> | |||
\gamma_2 = \frac{r_2 x_2^2}{k_2} + \frac{r_2 x_2 \alpha_{21} x_1}{k_2} - r_2x_2 + 2\beta_2^2x_2 | |||
</math> | |||
<math> | |||
\omega = \frac{2r_1x_1}{k_1} + \frac{2r_2x_2}{k_2} + \frac{r_1\alpha_{12}x_2}{k_1} + \frac{r_2\alpha_{21}x_1}{k_2} - r_1 - r_2 + \beta_1^2 + \beta_2^2 | |||
</math> | |||
</center> | |||
Discretizando a equação diferencial acima, usando que | |||
<center> | |||
<math> | |||
\frac{\partial P(x,t)}{\partial t} = \frac{P_{i,j}^{n+1} - P_{i,j}^{n}}{dt} | |||
</math> | |||
<math> | |||
\frac{\partial P(x,t)}{\partial x_1} = \frac{1}{2} \frac{P_{i+1,j}^{n} - P_{i-1,j}^{n}}{dx_1} | |||
</math> | |||
<math> | |||
\frac{\partial P(x,t)}{\partial x_2} = \frac{1}{2} \frac{P_{i,j+1}^{n} - P_{i,j-1}^{n}}{dx_2} | |||
</math> | |||
<math> | |||
\frac{\partial^2 P(x,t)}{\partial x_1^2} = \frac{P_{i+1,j}^{n} + P_{i-1,j}^{n} - 2P_{i,j}^{n}}{dx_1^2} | |||
</math> | |||
<math> | |||
\frac{\partial^2 P(x,t)}{\partial x_2^2} = \frac{P_{i,j+1}^{n} + P_{i,j-1}^{n} - 2P_{i,j}^{n}}{dx_2^2} | |||
</math> | |||
</center> | |||
e que <math> dx_1 = dx_2 </math>, chegamos, enfim, em | |||
<center> | |||
<math> | |||
P_{i,j}^{n+1} = P_{i,j}^{n}\left( 1 - \frac{2\delta_1 dt}{dx^2} - \frac{2\delta_2 dt}{dx^2} + \omega dt \right) + P_{i+1,j}^{n} \left( \frac{\delta_1 dt}{dx^2} + \frac{\gamma_1 dt}{2dx} \right) + P_{i,j+1}^{n} \left( \frac{\delta_2 dt}{dx^2} + \frac{\gamma_2 dt}{2dx} \right) + P_{i-1,j}^{n} \left( \frac{\delta_1 dt}{dx^2} - \frac{\gamma_1 dt}{2dx} \right) + P_{i,j-1}^{n} \left( \frac{\delta_2 dt}{dx^2} - \frac{\gamma_2 dt}{2dx} \right) | |||
</math> | |||
</center> | |||
que foi resolvida numericamente. | |||
Abaixo, temos um gráfico considerando duas populações, com constantes todas iguais e baixo ruído. O eixo das abcissas indica a população <math>x_1</math>, o eixo das ordenadas, a população <math>x_2</math> e a cor representa a probabilidade da população possuir aquele número de indivíduos. | |||
<center> | |||
[[Arquivo:Tmp.gif]] | |||
</center> | |||
== Código == | |||
Os principais programas utilizados no trabalho se encontram no repositório https://github.com/gugabXD/trab2-metcompC | |||
== Referências == | |||
# Scherer, CLÁUDIO. Métodos Computacionais da Física. 2010. | |||
Edição atual tal como às 23h07min de 2 de setembro de 2024
Introdução
As Equações de Lotka-Volterra fornecem um modelo para a previsão de sistemas biológicos considerando diversas relações entre populações. Exploraremos no vigente trabalho a relação de competitividade, juntamente da adição de um termo estocástico multiplicativo. Consideraremos duas e três populações, mostrando os gráficos de evolução temporal do número de indivíduos de cada espécie e os espaços de fase. Em todas as etapas serão mostrados os resultados considerando e desconsiderando o ruído para fins comparativos. Por fim, descreveremos o método de Fokker-Planck, utilizando um exemplo simples para a demonstração.
Equações para Duas Populações
Como uma primeira análise, considerando somente duas populações distintas, vamos explorar o modelo logístico, partindo das Equações de Lotka-Volterra, de duas espécies disputando um território, que pode ser descrito pelo seguinte par de relações:
Nesse par, e representam as duas populações consideradas; e indicam o crescimento inerente per-capita, a capacidade de uma espécie em se reproduzir; e retratam a capacidade de carga, o número de indivíduos limite que o meio ambiente consegue suportar considerando o nicho ecológico ao que a espécie pertence; e e , o efeito que a espécie um tem na espécie dois e vice-versa.
Para a adição de ruído ao sistema, vamos supor que o termo estocástico seja incorporado em cada equação de maneira a afetar somente a população ou a população , ou seja, estamos considerando que o ruído atinja cada população de maneira proporcional a sua quantidade de indivíduos em determinado período de tempo. Como um exemplo prático, podemos pensar no termo estocástico como a presença de um agente externo que infecte uma das populações isoladamente. Claro que o efeito resultante de existir uma doença se espalhando na espécie afeta o crescimento da espécie , entretanto esse efeito não é direto, sendo uma consequência da correlação entre o par de equações.
Além disso, antes de de fato colocarmos o fator estocástico nas equações, precisamos de explicar qual o tipo de ruído a ser inserido. Para tanto, será introduzido o ruído branco, que é definido a partir de suas propriedades estatísticas que configuram sua média e sua função de correlação temporal, podendo ser expressas matematicamente por
A primeira relação indica que o ruído branco possui média igual a zero, enquanto que a segunda indica o fato de os ruídos considerando diferentes tempos são independentes e, sendo assim, dá o nome branco ao ruído, pois a intensidade espectral de um processo estocástico é a Transformada de Fourier da função de correlação, sendo ela constante por se tratar de uma Delta de Dirac, logo todas as frequências estão presentes com mesma intensidade, com branco fazendo uma analogia a essa característica.
Portanto, podemos reescrever as relações supracitadas considerando o ruído como
com e sendo as amplitudes dos ruídos e e os ruídos brancos.
Resolução Numérica pelo Método de Itô
Para então resolvermos as equações numericamente, vamos recorrer ao cálculo diferencial estocástico. Iniciamos, para esse fim, tomando a forma de Langevin
Deveríamos, como próxima etapa, integrar ambos os lados da equação da seguinte forma
Como não podemos resolvê-la pelos métodos convencionais, pois torna a função não diferenciável apesar de ser contínua, utilizamos a relação
Essa troca se justifica pelo fato de estarmos trocando o argumento de B pela média entre os valores de X no início e no fim do intervalo de integração, correspondendo a uma melhor estimação. Agora, tomando a integral, ficamos com a aproximação
Por seguinte, expandimos B em série de Taylor, excluímos o termo de ordem maior que dt e fazemos a substituição por
Com isso, temos que a Equação diferencial de Itô é dada por
Portanto, partindo da nossa relação para
Temos, isolando
A partir disso, sabemos os coeficientes A(X(t),t) e B(X(t),t) de Langevin
Assim, substituindo os valores para encontrar a equação diferencial de Itô, obtemos
Analogamente, obtemos também a equação para a variável
Resultados
Caso Um
Com duas populações, vamos exemplificar nesta seção o caso em que a competitividade se dá de maneira igual, ou seja, todas as constantes possuem mesmo valor independentemente da população. A diferença, então, se dará a partir do ruído, que será maior para uma delas.
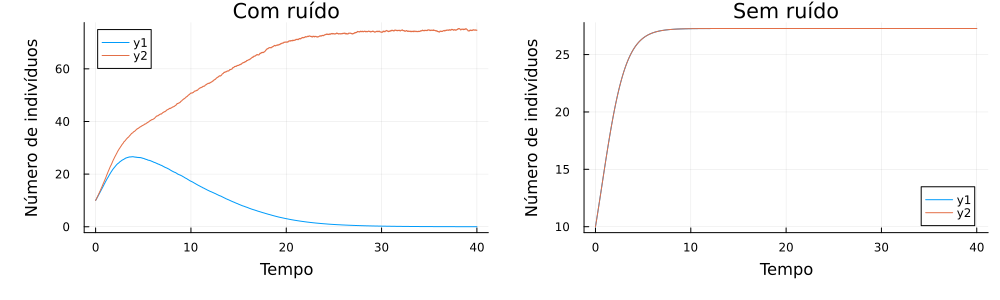
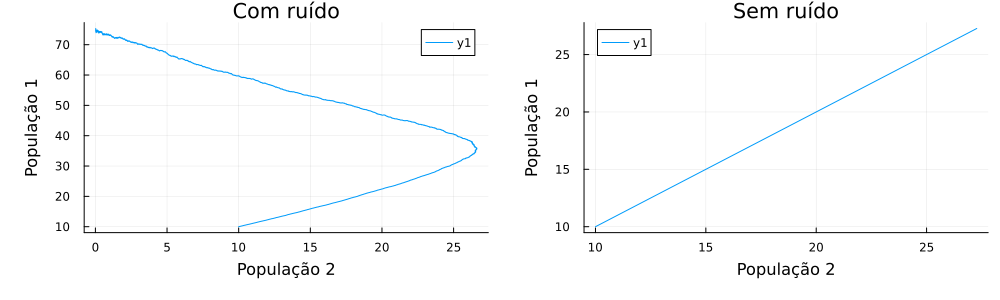
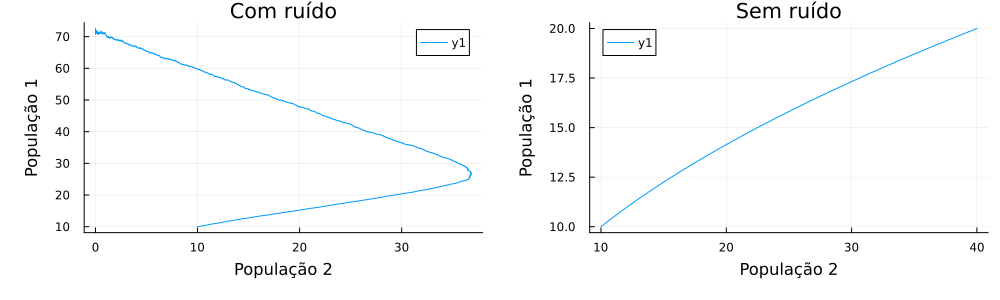
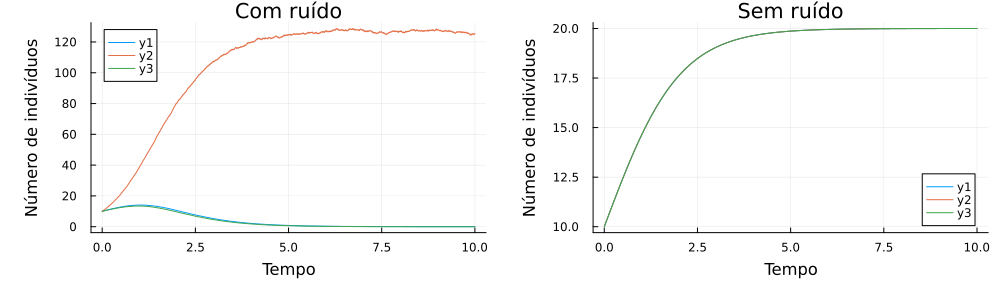
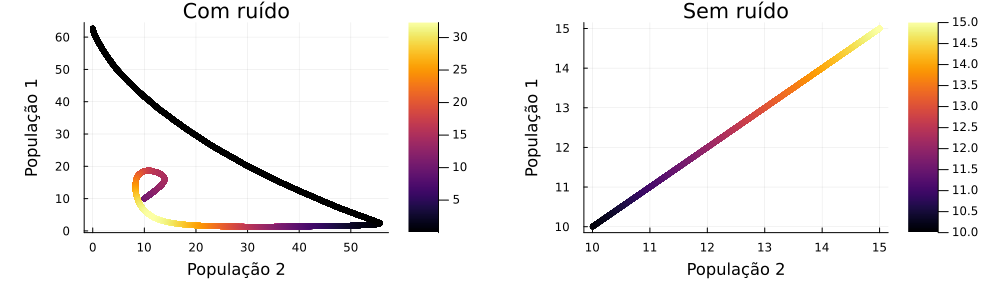
Utilizando = = = = 1, = = 60 e população inicial de 10 indivíduos, a evolução temporal e o espaço de fases do sistema de duas populações podem ser vistos nas figuras abaixo.
Podemos verificar que, a partir da adição de um ruído maior na população 2, a população 1 cedeu quando o tempo atingiu valor próximo a 30 unidades, comportamento este que não é visto no gráfico sem ruído, no qual as duas populações convivem de maneira igual e atingindo cada uma metade de sua população limite. Realizaram-se mais de 20 simulações e todas tiveram o mesmo efeito, com a população 2 prosperando em consequência do desaparecimento da população 1.
Caso Dois
Agora, consideraremos uma pequena variação nas constantes de crescimento das populações, com um aumento de duas vezes para . Todos os outros parâmetros são iguais ao Caso Um. Os resultados seguem nas figuras abaixo.
Mesmo com a população um possuindo taxa de crescimento duas vezes maior, a espécie com maior amplitude de ruído sobrevive ao final da simulação.
Equações para Três Populações
Os métodos de resolução numérica para três populações são completamente análogos aos métodos para duas populações; portanto, a matemática envolvida será omitida a partir de agora e somente serão discutidos os resultados. O conjunto de equações utilizado para três espécies distintas é
Resultados
Caso Um
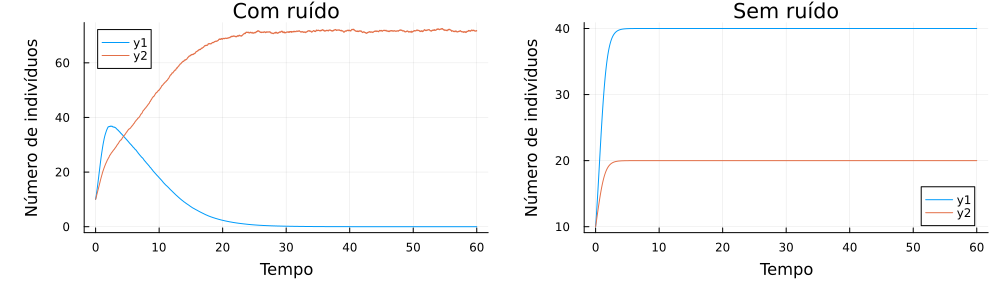
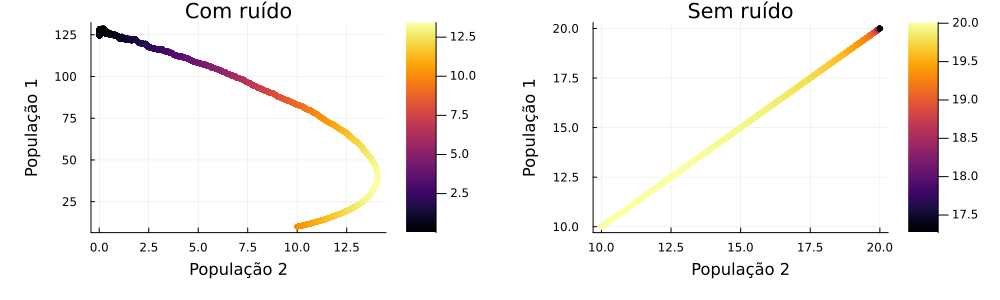
Como primeira análise, vamos ao caso análogo ao anterior de duas populações. Vamos considerar espécies semelhantes, trocando entre elas somente o fator de amplitude do ruído, com o maior fator sendo da população 2. Utilizamos = = = 60, população inicial de 10 indivíduos e as outras constantes como um. As figuras a seguir mostram a evolução temporal e o espaço de fases do sistema.
Podemos verificar que, assim como na seção anterior, a população com maior fator de ruído prosperou enquanto que as outras tiveram sua extinção em um tempo de 5 unidades. Quando desconsideramos o ruído, vemos que as três espécies convivem com mesmo comportamento populacional.
Caso Dois
Para um segundo caso, vamos considerar os mesmos parâmetros de antes, modificando apenas os coeficientes entre as populações, dados na seguinte tabela.
| 1 | 2 | 1 | |
| 1 | 1 | 2 | |
| 2 | 1 | 1 |
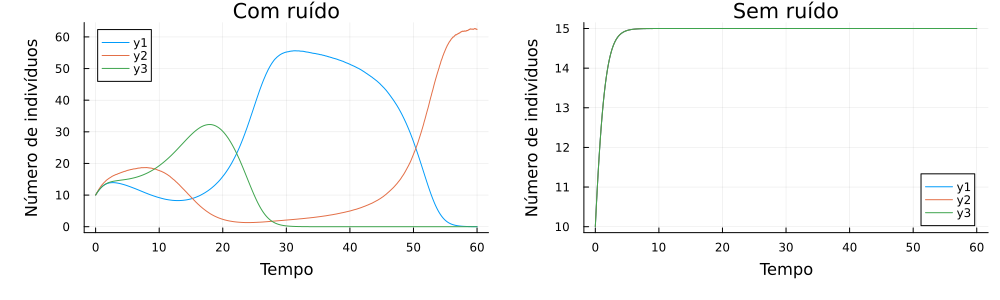
Eles indicam que a população 1 tem dominância sobre a população 2, a população 2 tem dominância sobre a população 3 e a população 3 tem dominância sobre a população 1. As imagens podem ser vistas a seguir.
Vemos que, mesmo considerando as relações de dominância, a população com maior ruído sobressai no final, sendo a única espécie viva ao final da simulação.
Método de Fokker-Planck
A Equação de Fokker-Planck trata da equação diferencial da distribuição de probabilidade das variáveis de um sistema de Equações Diferenciais Estocásticas. Avaliaremos sua aplicação no sistema Lotka-Volterra competitivo para duas populações.
Para um processo estocástico vetorial , a equação de Fokker-Planck tem a forma
em que
e
Assim, para o nosso caso, temos
Resolvendo as derivadas por regra do produto e separando nas derivadas parciais de ficamos com
com
Discretizando a equação diferencial acima, usando que
e que , chegamos, enfim, em
que foi resolvida numericamente.
Abaixo, temos um gráfico considerando duas populações, com constantes todas iguais e baixo ruído. O eixo das abcissas indica a população , o eixo das ordenadas, a população e a cor representa a probabilidade da população possuir aquele número de indivíduos.
Código
Os principais programas utilizados no trabalho se encontram no repositório https://github.com/gugabXD/trab2-metcompC
Referências
- Scherer, CLÁUDIO. Métodos Computacionais da Física. 2010.













































![{\displaystyle X=[X_{1},X_{2},...,X_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8fa2882081eebf5b8d5c0216e5d4ddfa2e6bf02)
![{\displaystyle {\frac {\partial P(x,t)}{\partial t}}=\sum _{i=1}^{n}{\frac {\partial [K_{i}(x,t)P(x,t)]}{\partial x_{i}}}+{\frac {1}{2}}\sum _{i,j=1}^{n}{\frac {\partial ^{2}[D_{ij}(x,t)P(x,t)]}{\partial x_{i}\partial x_{j}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3169037e86a92c63272bee39f9eb1edbe471bde)


![{\displaystyle {\frac {\partial P(x_{1},x_{2},t)}{\partial t}}=-{\frac {\partial }{\partial x_{1}}}\left[r_{1}x_{1}\left(1-{\frac {x_{1}+\alpha _{12}x_{2}}{k_{1}}}\right)P(x_{1},x_{2},t)\right]-{\frac {\partial }{\partial x_{2}}}\left[r_{2}x_{2}\left(1-{\frac {x_{2}+\alpha _{21}x_{1}}{k_{2}}}\right)P(x_{1},x_{2},t)\right]+{\frac {1}{2}}\beta _{1}^{2}{\frac {\partial ^{2}x_{1}^{2}P(x_{1},x_{2},t)}{\partial x_{1}^{2}}}+{\frac {1}{2}}\beta _{2}^{2}{\frac {\partial ^{2}x_{2}^{2}P(x_{1},x_{2},t)}{\partial x_{2}^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd42653a16eb2df3d5246fbdb34cac17cd81f5e8)