Lançamento Oblíquo Estocástico: mudanças entre as edições
| (25 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 79: | Linha 79: | ||
<math> | <math> | ||
\frac{dX}{dt} = A(X(t)) + B(X(t))\xi(t) | \frac{dX}{dt} = A(X(t)) + B(X(t))\xi(t), | ||
</math> | |||
onde | |||
<math> | |||
X = \begin{pmatrix} | |||
x \\ y \\ v_x \\ v_y | |||
\end{pmatrix}, \quad | |||
A = \begin{pmatrix} | |||
v_x \\ v_y \\ -k v_x \\ -g-kv_y | |||
\end{pmatrix}, \quad | |||
B = \begin{pmatrix} | |||
0 & 0 & 0 & 0 \\ | |||
0 & 0 & 0 & 0 \\ | |||
0 & 0 & \beta e^{-\frac{y}{H}} & 0 \\ | |||
0 & 0 & 0 & \beta e^{-\frac{y}{H}} | |||
\end{pmatrix}, \quad | |||
\xi = \begin{pmatrix} | |||
0 \\ 0 \\ \xi_x(t) \\ \xi_y(t) | |||
\end{pmatrix} | |||
</math> | </math> | ||
| Linha 88: | Linha 108: | ||
</math> | </math> | ||
onde <math>\xi(t)dt = dW(t)</math> é o incremento de Wiener, um processo estocástico com distribuição gaussiana de largura <math>\sqrt{dt}</math>. | onde <math>\xi(t)dt = dW(t)</math> é o incremento de Wiener, um processo estocástico com distribuição gaussiana de largura <math>\sqrt{dt}</math>. Escrevendo a equação em diferenças finitas e substituindo os valores de <math>A(X(t))</math> e de <math>B</math> têm-se: | ||
<math> | <math> | ||
\Delta x_i = v_{x_i} \Delta t | |||
</math> | </math> | ||
<math> | <math> | ||
\Delta | \Delta v_{x_i} = -k v_{x_i} \Delta t + \beta \Delta W_{x_i} | ||
</math> | </math> | ||
<math> | <math> | ||
\Delta | \Delta y_i = v_{y_i} \Delta t | ||
</math> | </math> | ||
<math> | <math> | ||
\Delta v_{ | \Delta v_{y_i} = \left(-g -k v_{x_i} \right) \Delta t + \beta \Delta W_{x_i} | ||
</math> | </math> | ||
Entretanto, o termo <math>B(X,t)</math> depende do processo estocástico e o ruído é dito multiplicativo, assim, devemos utilizar um cálculo estocástco especial, por exemplo o cálculo de Itô e de Stratonovich. No cálculo de Stratonovich, as regras de integração, diferenciação, mudança de variáveis etc, se mantém as mesmas do cálculo usual, e a equação é escrita como: | |||
<math> | <math> | ||
dX(t) = A(X(t))dt + B(X(t))dW(t), | |||
</math> | </math> | ||
com o detalhe que o argumento de <math>B(X(t))</math> é, na realidade, calculado na média de X entre os limites do intervalo de integração. Ou seja, ao escrever a equação em diferenças finitas, obtém-se: | |||
<math> | <math> | ||
\Delta | \Delta X(t) = A(X(t)) \Delta t + B\left(X(t) + \frac{1}{2} \Delta X(t)\right) \Delta W(t). | ||
</math> | </math> | ||
Agora, é necessário explicitar o <math>\Delta X(t)</math> na equação acima, porém a dependência de <math>B(X(t))</math> não é linear em relação à altura, o que torna inviável esse procedimento. | |||
| Linha 130: | Linha 148: | ||
</math> | </math> | ||
Após a substituição dos valores de | No caso em que <math>B</math> não depende de <math>X(t)</math>, a derivada que aparece na equação é zero e é recuperado o caso de ruído aditivo já mencionado. Aqui, vale ressaltar que <math>B(X(t))</math> é uma matriz e está sendo derivada com relação ao vetor <math>X(t)</math>, então o cálculo para as componentes de <math>X_i(t)</math> são: | ||
<math> | |||
dX_i(t) = A^{(I)}_i(X(t))dt + \sum_{\alpha=1}^m B_{i,\alpha}(X(t)) \bullet dW_\alpha(t), | |||
</math> | |||
onde | |||
<math> | |||
A^{(I)}_i(X(t)) = A_i(X(t)) + \frac{1}{2} \sum_{j=1}^n \sum_{\alpha=1}^m \frac{\partial B_{i,\alpha}}{\partial X_j} B_{j,\alpha}(X(t)). | |||
</math> | |||
Após a substituição dos valores de <math>A_i(X(t))</math> e <math>B_i(X(t))</math>, obtêm-se as seguintes expressões: | |||
<math> | <math> | ||
| Linha 137: | Linha 167: | ||
<math> | <math> | ||
\Delta v_{x_i} = -k v_{x_i} \Delta t + \beta e^{- \frac{y(t)}{H}} \Delta | \Delta v_{x_i} = \left[ - k v_{x_i} -\frac{\beta^2}{2H} e^{-\frac{2}{H} y_i} \right] \Delta t + \beta e^{- \frac{y(t)}{H}} \Delta W_{x_i} | ||
</math> | </math> | ||
| Linha 145: | Linha 175: | ||
<math> | <math> | ||
\Delta v_{y_i} = \left | \Delta v_{y_i} = \left[ -g - k v_{x_i} -\frac{\beta^2}{2H} e^{-\frac{2}{H} y_i} \right] \Delta t + \beta e^{- \frac{y_i}{H}} \Delta W_{y_i} | ||
</math> | </math> | ||
É importante ressaltar que os incrementos de Wiener que aparecem nas equações para velocidade são independentes entre si, isto é, deverá ser gerado duas variáveis aleatórias com distribuição gaussiana de largura <math>\sqrt{\Delta t}</math>. Além disso, um detalhe interessante é que a equação para <math>\Delta v_x</math> é semelhante à equação para <math>\Delta v_y</math> em que <math>g = 0</math>. | |||
== Resultados == | == Resultados == | ||
Aqui temos alguns gráficos comparativos, nesses dois primeiros comparamos os dois modelos para a mesma distribuição de ruídos. | |||
[[File:multeuler.gif|400px|Figura 1 - Ruído multiplicativo]][[File:Aditivo_euler.gif|400px|Figura 2 - Ruído aditivo]] | |||
Nas figuras abaixo podemos ver as trajetórias de certo objeto para ruído aditivo e ruído multiplicativo para diferentes distribuições. | |||
[[File:Ruido_multiplicativo2.gif|400px|Figura 1 - Ruído multiplicativo]][[File:Ruido_aditivo2.gif|400px|Figura 2 - Ruído aditivo]] | |||
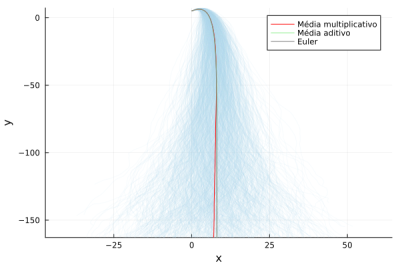
Esperávamos que as média para ruído aditivo e multiplicativos fossem iguais, dado que o ruído não interfere no cálculo da média pois a probabilidade de puxar em qualquer direção é a mesma, porém como pode ser visto no gráfico abaixo há divergência para o ruído multiplicativo. | |||
[[File:N=1000_SCC2.png|400px|Figura 3 - Médias para N = 1000]] | |||
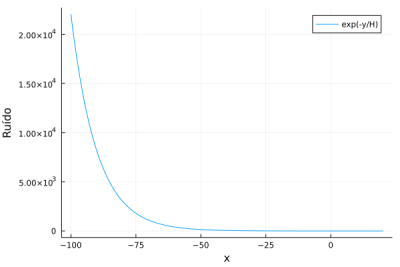
Tanto a divergência da médias como o aumento da dispersão da trajetórias podem ser explicados pelo modelo que estamos usando na EDE-ito <math>(\beta e^{- \frac{y_i}{H}})</math>, nesse modelo conforme temos y variando para valores negativos a exponencial explode consequentemente temos aumento na intensidade do ruído, esse aumento pode ser observado no gráfico abaixo. | |||
[[File:Exp.png|400px|Figura 7 - exp]] | |||
Temos que para poucos passos o ganho do ruído em qual direção causara grande divergência, ou seja, para termos vermos a convergência para média do ruído multiplicativo precisamos incrementar o número de trajetórias, a figura a seguir foi feita para um aumento de dez vezes no número de passos comparado ao da figura anterior. | |||
[[File:N=10000_SCC2.png|400px|Figura 4 - Médias para N = 10000]] | |||
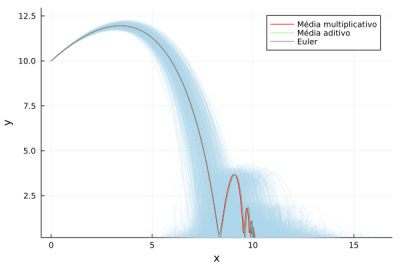
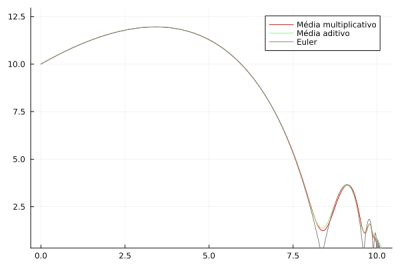
Nos gráficos abaixo temos as trajetórias para o ruído multiplicativo, as médias para os dois métodos e a solução por euler levando em conta o solo, para as trajetória é visível a dispersão em torno da solução de euler que acontece por causa do ruído, porém como comentado anteriormente essa dispersão não influência na trajetória média, da mesma forma que as duas primeiras figuras conforme a diminuição das velocidades pelo termo dissipativo temos maior influência do ruído no trajeto que pode até mesmo ocasionar em um retorno do objeto na direção da posição inicial porém a média continua somente para a direita. | |||
[[File:N=1000_CCC2.png|400px|Figura 5 - Médias para N = 1000]] | |||
Agora para um maior valor de ruído podemos observar o gráfico a seguir, onde notamos que a média, na região de contato com o solo, fica acima da solução de euler, isso ocorre pela condição de contorno que estamos utilizando, quando a posição da partícula chega em zero invertemos o sinal da velocidade mas ao fazermos isso alteramos também o ruído que posteriormente faria a partícula tender para baixo porém agora, com a troca de sinal, estará contribuído para cima assim temos uma deslocamento da média para cima. Neste caso temos que o deslocamento para o aditivo é maior do que o do multiplicativo logo o ruído do aditivo é mais intenso. | |||
[[File:Ruidoalto2.png|400px|Figura 6 - Médias para ruido alto]] | |||
Edição atual tal como às 17h59min de 19 de agosto de 2024
O lançamento oblíquo é um clásico problema da mecanica, onde um projétil e lançado com velocidade inicial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} em uma direção que faz um angulo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} com a horizontal. Nesse casso iremos considerar o movimento com arrasto em que a força de resistencia do ar é oposta ao movimento e proporcional a velocidade
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_{Ar}=-kmv }
O objetivo é descrever o movimento do projétil em duas dimensões, levando em consideração tanto a força da gravidade quanto a resistência do ar então adicionar um termo de ruido no sistema e analizar seu comportamento.
Equações de Movimento
Começamos decompondo as velocidades nas direções x e y
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{x}=v \cos(\theta) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{y}=v \sin(\theta) }
Para as equações de movimento usamos a segunda lei de Newton nas componentes horizontais e verticais
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\frac{d^2 x}{dt^2}=-kmv_{x} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\frac{d^2 y}{dt^2}=-mg-kmv_{y} }
onde:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} é a massa do projétil
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} é a aceleração da gravidade
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} é o coeficiente de arrasto
Introduzindo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{x}=\frac{dx}{dt}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{y}=\frac{dy}{dt}} podemos reescrever as equações como diferenciais de primeira ordem.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv_{x}}{dt}=-kv_{x} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv_{y}}{dt}=-g-kv_{y} }
Essas E.D. possuem solução analitica bastando integrar nos limites adequados. A integração numérica por Euler é dirta a partir das relações a cima e nos da uma trajetoria para comparação quando adicionar o termo de ruido:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{x,j+1}=v_{x,j}-kv_{x,j}dt }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{y,j+1}=v_{y,j}-g dt- kv_{y,j}dt }
Utilizando as seguintes condições iniciais Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{0}=0} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{0}=0} podemos atualizar a posição
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{x}=\frac{dx}{dt} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{j+1}=x_{j}+v_{x,j}dt }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{y}=\frac{dy}{dt} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{j+1}=y_{j}+v_{y,j}dt }
Para modelar o ruído produzido pela densidade do ar, consideramos dois regimes. No primeiro, assumimos que a densidade é constante ao longo da trajetória, ou seja, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=\rho_{0}} e, portanto, trataremos o problema como uma EDE com ruído aditivo, onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_{(X(t),t)}=\rho_{0}=\beta} . Na segunda situação, consideramos que a densidade varia com a altitude do projétil, seguindo a relação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=\rho_{0}e^{-\frac{y}{H}}} e, nesse caso, abordaremos como uma EDE com ruído multiplicativo, onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_{(X(t),t)}=\rho_{(X(t))}=\beta e^{-\frac{y}{H}}} .
Equação diferencial estocástica
A equação diferencial estocástica a ser resolvida é:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dX}{dt} = A(X(t)) + B(X(t))\xi(t), }
onde
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle X = \begin{pmatrix} x \\ y \\ v_x \\ v_y \end{pmatrix}, \quad A = \begin{pmatrix} v_x \\ v_y \\ -k v_x \\ -g-kv_y \end{pmatrix}, \quad B = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & \beta e^{-\frac{y}{H}} & 0 \\ 0 & 0 & 0 & \beta e^{-\frac{y}{H}} \end{pmatrix}, \quad \xi = \begin{pmatrix} 0 \\ 0 \\ \xi_x(t) \\ \xi_y(t) \end{pmatrix} }
Caso o termo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(X,t)} fosse uma constante, exemplo em que a densidade do ar não muda significativamente, o ruído é dito aditivo. Então, a integração da equação é direta, resultando em:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dX(t) = A(X(t))dt + BdW(t), }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi(t)dt = dW(t)} é o incremento de Wiener, um processo estocástico com distribuição gaussiana de largura Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{dt}} . Escrevendo a equação em diferenças finitas e substituindo os valores de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(X(t))} e de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} têm-se:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x_i = v_{x_i} \Delta t }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta v_{x_i} = -k v_{x_i} \Delta t + \beta \Delta W_{x_i} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta y_i = v_{y_i} \Delta t }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta v_{y_i} = \left(-g -k v_{x_i} \right) \Delta t + \beta \Delta W_{x_i} }
Entretanto, o termo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(X,t)}
depende do processo estocástico e o ruído é dito multiplicativo, assim, devemos utilizar um cálculo estocástco especial, por exemplo o cálculo de Itô e de Stratonovich. No cálculo de Stratonovich, as regras de integração, diferenciação, mudança de variáveis etc, se mantém as mesmas do cálculo usual, e a equação é escrita como:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dX(t) = A(X(t))dt + B(X(t))dW(t), }
com o detalhe que o argumento de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(X(t))} é, na realidade, calculado na média de X entre os limites do intervalo de integração. Ou seja, ao escrever a equação em diferenças finitas, obtém-se:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta X(t) = A(X(t)) \Delta t + B\left(X(t) + \frac{1}{2} \Delta X(t)\right) \Delta W(t). }
Agora, é necessário explicitar o Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta X(t)} na equação acima, porém a dependência de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(X(t))} não é linear em relação à altura, o que torna inviável esse procedimento.
Com isso, a atenção volta-se para o cálculo de Itô, dado por:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dX(t) = \left[A(X(t)) + \frac{1}{2} \frac{\partial B}{\partial X}B(X(t))\right] dt + B(X(t)) \bullet dW(t) }
No caso em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} não depende de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle X(t)} , a derivada que aparece na equação é zero e é recuperado o caso de ruído aditivo já mencionado. Aqui, vale ressaltar que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(X(t))} é uma matriz e está sendo derivada com relação ao vetor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle X(t)} , então o cálculo para as componentes de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_i(t)} são:
onde
Após a substituição dos valores de e , obtêm-se as seguintes expressões:
É importante ressaltar que os incrementos de Wiener que aparecem nas equações para velocidade são independentes entre si, isto é, deverá ser gerado duas variáveis aleatórias com distribuição gaussiana de largura . Além disso, um detalhe interessante é que a equação para é semelhante à equação para em que .
Resultados
Aqui temos alguns gráficos comparativos, nesses dois primeiros comparamos os dois modelos para a mesma distribuição de ruídos.
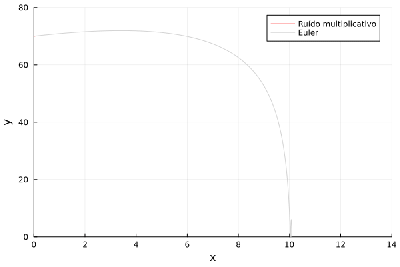
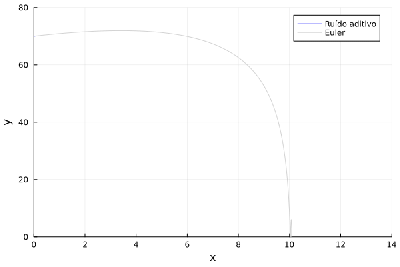
Nas figuras abaixo podemos ver as trajetórias de certo objeto para ruído aditivo e ruído multiplicativo para diferentes distribuições.
Esperávamos que as média para ruído aditivo e multiplicativos fossem iguais, dado que o ruído não interfere no cálculo da média pois a probabilidade de puxar em qualquer direção é a mesma, porém como pode ser visto no gráfico abaixo há divergência para o ruído multiplicativo.
Tanto a divergência da médias como o aumento da dispersão da trajetórias podem ser explicados pelo modelo que estamos usando na EDE-ito , nesse modelo conforme temos y variando para valores negativos a exponencial explode consequentemente temos aumento na intensidade do ruído, esse aumento pode ser observado no gráfico abaixo.
Temos que para poucos passos o ganho do ruído em qual direção causara grande divergência, ou seja, para termos vermos a convergência para média do ruído multiplicativo precisamos incrementar o número de trajetórias, a figura a seguir foi feita para um aumento de dez vezes no número de passos comparado ao da figura anterior.
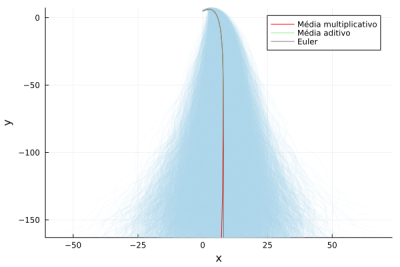
Nos gráficos abaixo temos as trajetórias para o ruído multiplicativo, as médias para os dois métodos e a solução por euler levando em conta o solo, para as trajetória é visível a dispersão em torno da solução de euler que acontece por causa do ruído, porém como comentado anteriormente essa dispersão não influência na trajetória média, da mesma forma que as duas primeiras figuras conforme a diminuição das velocidades pelo termo dissipativo temos maior influência do ruído no trajeto que pode até mesmo ocasionar em um retorno do objeto na direção da posição inicial porém a média continua somente para a direita.
Agora para um maior valor de ruído podemos observar o gráfico a seguir, onde notamos que a média, na região de contato com o solo, fica acima da solução de euler, isso ocorre pela condição de contorno que estamos utilizando, quando a posição da partícula chega em zero invertemos o sinal da velocidade mas ao fazermos isso alteramos também o ruído que posteriormente faria a partícula tender para baixo porém agora, com a troca de sinal, estará contribuído para cima assim temos uma deslocamento da média para cima. Neste caso temos que o deslocamento para o aditivo é maior do que o do multiplicativo logo o ruído do aditivo é mais intenso.





![{\displaystyle \Delta v_{x_{i}}=\left[-kv_{x_{i}}-{\frac {\beta ^{2}}{2H}}e^{-{\frac {2}{H}}y_{i}}\right]\Delta t+\beta e^{-{\frac {y(t)}{H}}}\Delta W_{x_{i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cfbf421710211b96ecddeb21ffceb83b1cee58a)

![{\displaystyle \Delta v_{y_{i}}=\left[-g-kv_{x_{i}}-{\frac {\beta ^{2}}{2H}}e^{-{\frac {2}{H}}y_{i}}\right]\Delta t+\beta e^{-{\frac {y_{i}}{H}}}\Delta W_{y_{i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60ef770be1cf217daf1f705501efca9958af66f2)