Equação de Ginzburg-Landau complexa: mudanças entre as edições
Sem resumo de edição |
|||
| (19 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 5: | Linha 5: | ||
</math> | </math> | ||
Em especial, para <math>b = 0</math> e <math>c = 0</math>, ela se reduz para a equação de Ginzburg-Landau real. E, para <math>b \rightarrow + \infty </math> e <math>c \rightarrow + \infty</math>, ela se reduz à equação de Schrödinger não linear. | Em especial, para <math>b = 0</math> e <math>c = 0</math>, ela se reduz para a equação de Ginzburg-Landau real. E, para <math>b \rightarrow + \infty </math> e <math>c \rightarrow + \infty</math>, ela se reduz à equação de Schrödinger não linear. Essa equação descreve uma variedade enorme de fenômenos, como: | ||
* Ondas não lineares; | * Ondas não lineares; | ||
| Linha 13: | Linha 13: | ||
* Condensado de Bose-Einstein. | * Condensado de Bose-Einstein. | ||
== | Neste trabalho será estudada a equação de Ginzburg-Landau complexa em duas dimensões com condições de contorno periódicas. | ||
== Equação == | |||
[[File:Phase_space_circle.png|thumb|right|Figura 1 - Espaço de fase do oscilador harmônico. Fonte - Cross, M., & Greenside, H. (2009)]] | [[File:Phase_space_circle.png|thumb|right|Figura 1 - Espaço de fase do oscilador harmônico. Fonte - Cross, M., & Greenside, H. (2009)]] | ||
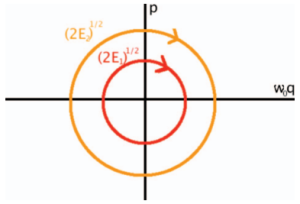
É possível | É possível obter a CGLE a partir do oscilador linear harmônico por meio de argumentos de simetria, encontrando a equação de Stuart-Landau, e, em seguida, considerando um sistema estendido no espaço. A energia de um oscilador harmônico é expressa pela equação abaixo, onde <math>E</math> é a energia, <math>q</math> e <math>p</math> a coordenada e seu respectivo momento, <math>m</math> é a massa e <math>\omega_0</math> a frequência angular | ||
<math> | <math> | ||
| Linha 78: | Linha 80: | ||
<math> | <math> | ||
\dot{A} = \mu (\sigma_1 + \omega_1) A - (g_r + ig_i)|A|^2 A | \dot{A} = \mu (\sigma_1 + i\omega_1) A - (g_r + ig_i)|A|^2 A | ||
</math> | </math> | ||
| Linha 109: | Linha 111: | ||
\frac{A_{i,j}^{N+1} - A_{i,j}^{N}}{\Delta t} = \alpha(\frac{A_{i+1,j}^{N} - 2*A_{i,j}^{N} + A_{i-1,j}^{N}}{\Delta x^2}+\frac{A_{i,j+1}^{N} - 2*A_{i,j}^{N} + A_{i,j-1}^{N}}{\Delta y^2}) + A_{i,j}^{N} - \beta A_{i,j}^{N}|A_{i,j}^{N}|^2. | \frac{A_{i,j}^{N+1} - A_{i,j}^{N}}{\Delta t} = \alpha(\frac{A_{i+1,j}^{N} - 2*A_{i,j}^{N} + A_{i-1,j}^{N}}{\Delta x^2}+\frac{A_{i,j+1}^{N} - 2*A_{i,j}^{N} + A_{i,j-1}^{N}}{\Delta y^2}) + A_{i,j}^{N} - \beta A_{i,j}^{N}|A_{i,j}^{N}|^2. | ||
</math> | </math> | ||
[[File:newplot.png|thumb|150px|right|Figura 2 - Condições de contorno periódicas em duas dimensões.]] | |||
Agora reorganizando a equação para deixar o tempo futuro na esquerda e o tempo atual na direita e considerando que os passos na direção x tem o mesmo tamanho do que os na direção y (<math>\Delta y = \Delta x</math>), chegamos em : | Agora reorganizando a equação para deixar o tempo futuro na esquerda e o tempo atual na direita e considerando que os passos na direção x tem o mesmo tamanho do que os na direção y (<math>\Delta y = \Delta x</math>), chegamos em : | ||
<math> | <math> | ||
A_{i,j}^{N+1} = A_{i,j}(1+\Delta t(1-\beta|A_{i,j}|^2))+\frac{\Delta t \alpha}{\Delta x^2}(A_{i+1,j}+A_{i-1,j}+A_{i,j+1}+A_{i,j-1} - 4*A_{i,j}) | A_{i,j}^{N+1} = A_{i,j}(1+\Delta t(1-\beta|A_{i,j}|^2))+\frac{\Delta t \alpha}{\Delta x^2}(A_{i+1,j}+A_{i-1,j}+A_{i,j+1}+A_{i,j-1} - 4*A_{i,j}) | ||
</math> | </math> | ||
Para as condições de contorno foram utilizados condições periódicas tal que na região de x usamos que quando | Para as condições de contorno foram utilizados condições periódicas tal que na região de x usamos que quando | ||
| Linha 126: | Linha 128: | ||
== Soluções == | == Soluções == | ||
[[File:diagrama_de_fase.png|thumb| | [[File:diagrama_de_fase.png|thumb|720px|upright|Figura 3 - Diagrama de fase para soluções da CGLE [3].]] | ||
A partir da variação dos parâmetros <math>b</math> e <math>c</math> temos regiões que implicam em diferentes soluções para a CGLE, nossa ideia principal foi começar com condição inicial de onda plana e criar alguma perturbação na onda, dependendo da região em que estamos no diagrama de fase a perturbação nos levara para diferentes tipos de solução sendo elas: | A partir da variação dos parâmetros <math>b</math> e <math>c</math> temos regiões que implicam em diferentes soluções para a CGLE, nossa ideia principal foi começar com condição inicial de onda plana e criar alguma perturbação na onda, dependendo da região em que estamos no diagrama de fase a perturbação nos levara para diferentes tipos de solução sendo elas: | ||
*Solução de onda plana | *Solução de onda plana | ||
*Líquido de vórtices | *Líquido de vórtices | ||
*Vidro de vórtices | *Vidro de vórtices | ||
*Turbulência na amplitude ou Turbulência de defeitos | *Turbulência na amplitude ou Turbulência de defeitos | ||
A estabilidade da onda plana é delimitada pela condição de Benjamin-Feir-Newell, descrito pela linha teórica BFN no diagrama de fase, a condição para instabilidade é descrita por <math>1 + bc < 0</math>, ou seja, a esquerda da linha podemos encontrar soluções estáveis e a direita mesmo sem perturbações na condição inicial não é possível encontrar soluções de onda plana. É importante enfatizar que o teste para estabilidade de onda plana e para geração das soluções líquido de vórtices e vidro de vórtices se difere pela amplitude da perturbação na condição inicial, para perturbação suficientemente pequena nessa região a onda plana tende a se estabilizar e continuar como onda plana, por outro lado para perturbações de alta amplitude podemos chegar em outro tipo de solução. | |||
As duas linhas EI e AI são linhas computacionais-experimentais e representam respectivamente, o critério generalizado de Eckhaus que descreve a instabilidade convectiva de onda plana, e o critério de instabilidade absoluta da onda plana. Esses dois critérios são critérios de "ajuste" para a condição de BFN, a linha EI delimita a condição que ao perturbarmos uma região à esquerda dela teremos estabilidade da onda plana, enquanto a linha AI define a região onda é possível encontrar espirais, a direita dela as espirais não conseguem se manter pela alta oscilação de <math>|A|</math>. | |||
direita de | Existem dois tipos de soluções para perturbações suficientemente grandes que ocorrem na região de estabilidade da onda plana, líquido de vórtices e vidro de vórtices, a linha teórica OR regida por <math>(c - b)/(1 +c*b) = 0.845</math>, demarca a região onde podemos encontrar cada tipo de solução que podem ser diferenciadas pelo comportamento das espirais, nas duas regiões temos decaimento exponencial das interações entre os vórtices porém a direita da linha OR esse decaimento apenas módula as interações, de forma que temos espirais paradas no espaço, já a esquerda temos essas espirais se movendo no espaço. | ||
O regimes turbulência de defeito se diferencia por não existir a formação de defeitos, como comentado anteriormente a direita de AI não é possível encontrar espirais pelo regime ser altamente caótico, a linha T caracteriza a transição do estado de vidro de vórtice para dinâmico turbulento. | |||
L é uma linha proposta anteriormente que não é mais valida, demarcava a existência de outra dinâmica do sistema, também não mais valida, turbulência de fase, onde não era visto formação de defeitos na amplitude porém para sistemas grandes(L = 10000) foi visto que após um certo tempo o sistema colapsava e começava a gerar defeitos na solução. | |||
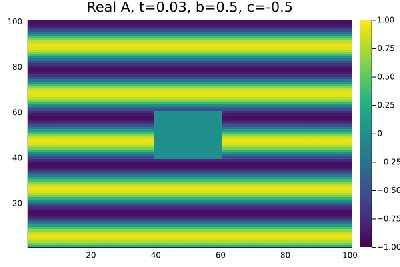
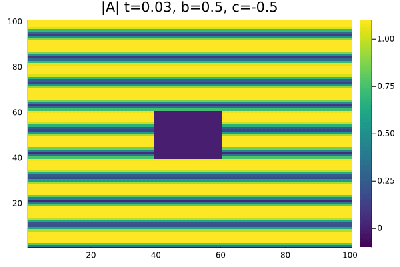
[[ | Quando definimos as condições iniciais de onda plana e perturbamos a região <math>x=[40,60]</math>, <math>y=[40,60]</math> diminuindo o seu valor em 0,3% , | ||
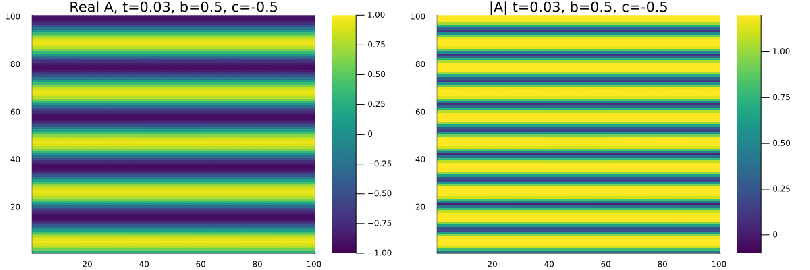
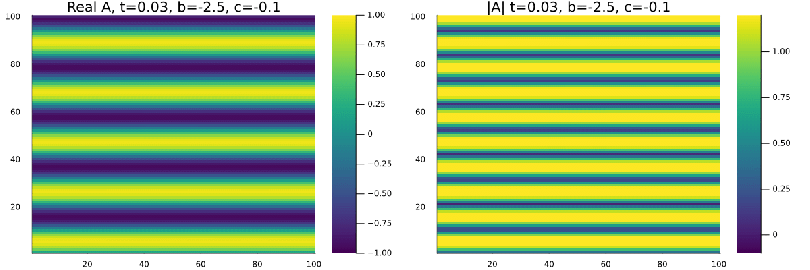
a onda plana se mantem estavel nas regioens de Liquido de Vortice <math>b=0.5</math>, <math>c=-0.5</math> e Vidro de vortice <math>b=-2.5</math>, <math>c=-0.1</math>. | |||
Dependendo dos parametors de c e b o valor maximo de perturbação pode aleterar, por exemplo, em <math>b=-1</math>, <math>c=-0.5</math> uma perturbação de 4% gerava regiões | |||
de defeitos que rapidamente se anulavam e o sistema retorava para estabilidade. | |||
[[File:EstavelLiquido.gif|810px|Figura 1 - Estabilidade Liquidos de Vortices]] | |||
[[File:VidroVortices.gif|400px|Figura 6 - | [[File:EstavelVidro.gif|810px|Figura 2 - Estabilidade Vidro de Vortices]] | ||
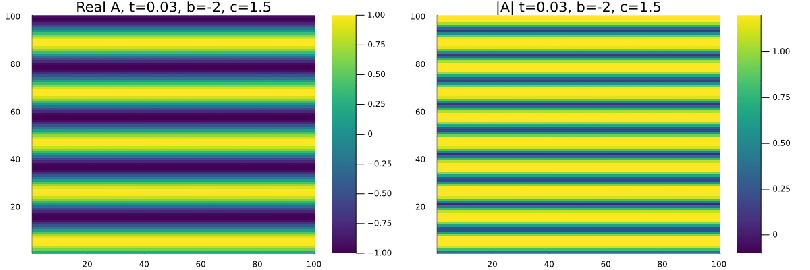
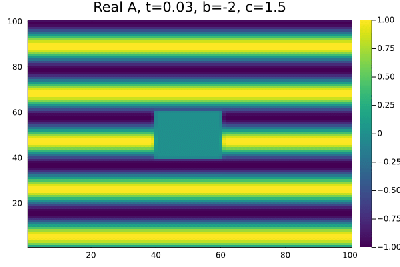
Ja na região de Turbulência de Amplitude <math>b=-2</math>, <math>c=1.5</math> a perturbação de 0,3% ja é suficiente para tornar a onda plana instaval resultando no comportamento caótico da (figura 3). | |||
Mesmo perturbações menores que 0,3% também resultam em turbulência . | |||
[[File:InstavelTurbu.gif|810px|Figura 3 - Instabilidade Turbulencia]] | |||
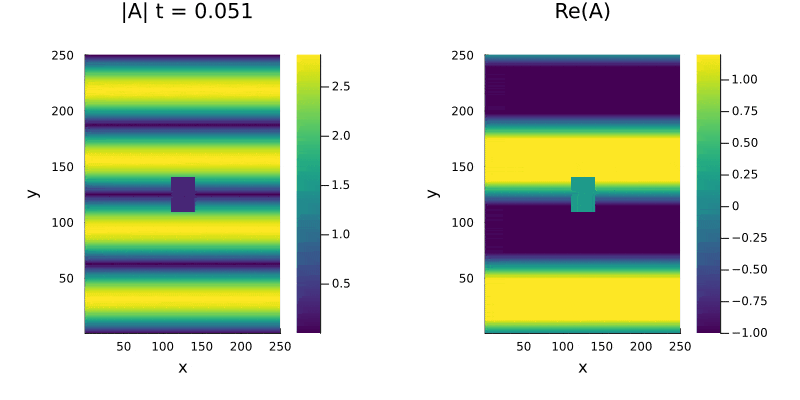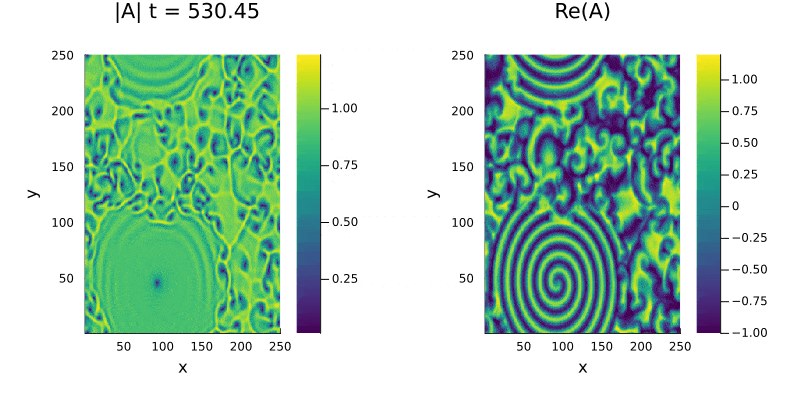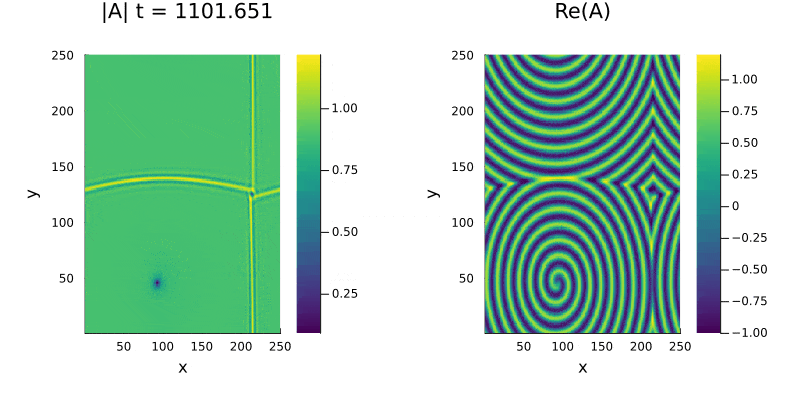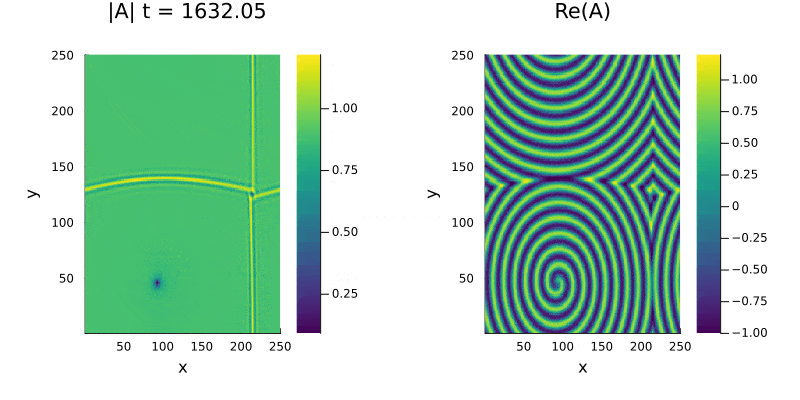
Para analizar o surgimento de espirais e suas caracteristicas utilizamos uma perturbação maior na mesma região (Liquido de Vórtices), o sistema apresenta simetria entre as espirais no gráfico da parte real e também | |||
percebemos a presença de defeitos no módulo de <math>A(x, y, t)</math> (figura 4). Os defeitos, caracterizados pela presença de um ponto nulo ou muito próximo de zero na amplitude, não se anulam mesmo após longos períodos de tempo | |||
[[File:LiquidoVortices.gif|400px|Figura 4 - Liquidos de Vortices]][[File:LiquidoVorticesAbs.gif|400px|Figura 5 - Modulo para Liquidos de Vortices]] | |||
Partindo das mesmas condições iniciais anteriores porém na região Vidro de Vórtices, o padrão de | |||
espirais muda, a simetria é perdida e em certas regioens podem se expandir formando frozen states. Outra característica é a presença de maior número de | |||
células de defeitos. É interessante ressaltar que os pontos defeitos se anulam somente aos pares. | |||
[[File:VidroVortices.gif|400px|Figura 6 - Vidro de Vortices]][[File:VidroVorticesAbs.gif|400px|Figura 7 - Modulo para Vidro de Vortices]] | |||
Por fim, na região chamada de Turbulência de Amplitude <math>b=-2</math>, <math>c=1.5</math> à direita da linha AI não encontramos espirais, as células de | Por fim, na região chamada de Turbulência de Amplitude <math>b=-2</math>, <math>c=1.5</math> à direita da linha AI não encontramos espirais, as células de | ||
| Linha 166: | Linha 178: | ||
[[File:TurbAmplitude.gif|400px|Figura 8 - | [[File:TurbAmplitude.gif|400px|Figura 8 - Turbulencia de Amplitude]][[File:TurbAmplitudeAbs.gif|400px|Figura 9 - Modulo para Turbulencia de Amplitude]] | ||
Estados congelados são a solução entre as linhas OR e T representam os vidro de vórtice, a lenta convergência para essa solução é dada pela proximidade da linha T, parâmetros b=-2.0 e c=0.6. | |||
[[File:Frozen_states.gif|800px|center|Figura | [[File:Frozen_states.gif|800px|center|Figura 10 - Estados congelados]] | ||
== Referências == | == Referências == | ||
[1] García-Morales, V., & Krischer, K. (2012). The complex Ginzburg–Landau equation: an introduction. Contemporary Physics, 53(2), 79–95. https://doi.org/10.1080/00107514.2011.642554 | [1] García-Morales, V., & Krischer, K. (2012). The complex Ginzburg–Landau equation: an introduction. Contemporary Physics, 53(2), 79–95. https://doi.org/10.1080/00107514.2011.642554 | ||
Edição atual tal como às 16h23min de 4 de julho de 2024
A equação de Ginzburg-Landau complexa (CGLE) é uma das equações não lineares mais estudadas da física. Ela oferece uma descrição geral de sistemas com uma fraca dependência não linear. Quando escrita de modo a minimizar o número de constantes, é dada pela equação abaixo:
Em especial, para e , ela se reduz para a equação de Ginzburg-Landau real. E, para e , ela se reduz à equação de Schrödinger não linear. Essa equação descreve uma variedade enorme de fenômenos, como:
- Ondas não lineares;
- Transições de fase de segunda ordem;
- Supercondutividade;
- Superfluidez;
- Condensado de Bose-Einstein.
Neste trabalho será estudada a equação de Ginzburg-Landau complexa em duas dimensões com condições de contorno periódicas.
Equação
É possível obter a CGLE a partir do oscilador linear harmônico por meio de argumentos de simetria, encontrando a equação de Stuart-Landau, e, em seguida, considerando um sistema estendido no espaço. A energia de um oscilador harmônico é expressa pela equação abaixo, onde é a energia, e a coordenada e seu respectivo momento, é a massa e a frequência angular
Ao realizar as seguintes mudanças de variáveis, e , a equação da energia produz trajetórias circulares no espaço de fase de e
Essa é uma importante simetria do oscilador harmônico linear, resultando que a sua energia é proporcional ao quadrado da amplitude de oscilação, não dependendo da fase. Isso sugere uma motivação, qual é o menor termo não linear que pode ser adicionado de modo a preservar essa simetria. Para tanto, o estado do sistema será descrito em coordenadas polares, onde é a amplitude e a fase
Define-se, então, a variável complexa , portanto a equação acima pode ser reescrita como
Ao realizar a transformação de variável , com , a equação acima permanece inalterada. Ou seja, a equação é invariante a rotações. Então, busca-se uma função não linear tal que
também seja invariante a rotações.
Então, perante às transformações e , a função deve satisfazer
para que seja possível fatorar o termo responsável pela rotação e obter novamente a equação original.
Considerando pequenas oscilações, é possível expandir em potências de e até a menor ordem possível que satisfaça a condição e que introduza uma não linearidade à equação. Com isso, obtém-se
Utilizando o resultado encontrado e expressando em coordenadas polares por meio de
Em seguida, muda-se para o referencial que gira com a mesma frequência do oscilador harmônico por meio da definição de . As novas equações obtidas são
Para encontrar a amplitude estacionária, pode-se tomar na equação, o que resulta na solução trivial e . Então, para que exista uma amplitude estacionária não nula, os sinais de e de devem ser opostos. Além disso, por inspeção observa-se que, caso e , pequenos valores de amplitude irão diminuir e grandes valores de amplitude irão aumentar, o que indica que a solução estacionária não trivial será instável. Portanto, define-se para , , com e . Por fim, ao voltar para a representação no plano complexo, chega-se em
Esta é a equação de Stuart-Landau. Para obter a equação complexa de Ginzburg-Landau, é necessário considerar um sistema espacialmente extenso, em que cada ponto é um oscilador modelado pela equação acima. Para isso, é adicionado um termo proporcional ao laplaciano de A, , cujo significado fica evidente ao discretizar a função. Ele computa a diferença de no sítio em questão com relação à média dos sítios vizinhos, resultando em uma tendência de pontos próximos oscilarem com amplitudes e fases semelhantes. Ao adicionar esse novo termo e redefinir as constantes de modo a reduzi-las sem perder as características importantes do sistema, chega-se na equação complexa de Ginzburg-Landau
Método FTCS
Para estudar o comportamento das soluções foi utilizados o método FTCS(Foward-Time Central-Space) explícito que consiste em discretizar o domínio temporal e o espacial da equação, resolvemos as derivadas espaciais por uma aproximação dos pontos vizinhos ao ponto que queremos encontrar, enquanto atualizamos a parte temporal, também por uma aproximação como na parte espacial, porém fazemos por diferenciação entre a taxa de variação (solução futura) e a solução atual. A partir da CGLE em duas dimensões:
para
Aplicamos o método da seguinte maneira:
Agora reorganizando a equação para deixar o tempo futuro na esquerda e o tempo atual na direita e considerando que os passos na direção x tem o mesmo tamanho do que os na direção y (), chegamos em :
Para as condições de contorno foram utilizados condições periódicas tal que na região de x usamos que quando
i=L+1 estaremos em i=1.
e para y, da mesma forma,
j=L+1 temos que j=1.
A figura 2 é a representação gráfica dessas condições.
Soluções
A partir da variação dos parâmetros e temos regiões que implicam em diferentes soluções para a CGLE, nossa ideia principal foi começar com condição inicial de onda plana e criar alguma perturbação na onda, dependendo da região em que estamos no diagrama de fase a perturbação nos levara para diferentes tipos de solução sendo elas:
- Solução de onda plana
- Líquido de vórtices
- Vidro de vórtices
- Turbulência na amplitude ou Turbulência de defeitos
A estabilidade da onda plana é delimitada pela condição de Benjamin-Feir-Newell, descrito pela linha teórica BFN no diagrama de fase, a condição para instabilidade é descrita por , ou seja, a esquerda da linha podemos encontrar soluções estáveis e a direita mesmo sem perturbações na condição inicial não é possível encontrar soluções de onda plana. É importante enfatizar que o teste para estabilidade de onda plana e para geração das soluções líquido de vórtices e vidro de vórtices se difere pela amplitude da perturbação na condição inicial, para perturbação suficientemente pequena nessa região a onda plana tende a se estabilizar e continuar como onda plana, por outro lado para perturbações de alta amplitude podemos chegar em outro tipo de solução.
As duas linhas EI e AI são linhas computacionais-experimentais e representam respectivamente, o critério generalizado de Eckhaus que descreve a instabilidade convectiva de onda plana, e o critério de instabilidade absoluta da onda plana. Esses dois critérios são critérios de "ajuste" para a condição de BFN, a linha EI delimita a condição que ao perturbarmos uma região à esquerda dela teremos estabilidade da onda plana, enquanto a linha AI define a região onda é possível encontrar espirais, a direita dela as espirais não conseguem se manter pela alta oscilação de .
Existem dois tipos de soluções para perturbações suficientemente grandes que ocorrem na região de estabilidade da onda plana, líquido de vórtices e vidro de vórtices, a linha teórica OR regida por , demarca a região onde podemos encontrar cada tipo de solução que podem ser diferenciadas pelo comportamento das espirais, nas duas regiões temos decaimento exponencial das interações entre os vórtices porém a direita da linha OR esse decaimento apenas módula as interações, de forma que temos espirais paradas no espaço, já a esquerda temos essas espirais se movendo no espaço.
O regimes turbulência de defeito se diferencia por não existir a formação de defeitos, como comentado anteriormente a direita de AI não é possível encontrar espirais pelo regime ser altamente caótico, a linha T caracteriza a transição do estado de vidro de vórtice para dinâmico turbulento.
L é uma linha proposta anteriormente que não é mais valida, demarcava a existência de outra dinâmica do sistema, também não mais valida, turbulência de fase, onde não era visto formação de defeitos na amplitude porém para sistemas grandes(L = 10000) foi visto que após um certo tempo o sistema colapsava e começava a gerar defeitos na solução.
Quando definimos as condições iniciais de onda plana e perturbamos a região , diminuindo o seu valor em 0,3% ,
a onda plana se mantem estavel nas regioens de Liquido de Vortice , e Vidro de vortice , .
Dependendo dos parametors de c e b o valor maximo de perturbação pode aleterar, por exemplo, em , uma perturbação de 4% gerava regiões
de defeitos que rapidamente se anulavam e o sistema retorava para estabilidade.
Ja na região de Turbulência de Amplitude , a perturbação de 0,3% ja é suficiente para tornar a onda plana instaval resultando no comportamento caótico da (figura 3). Mesmo perturbações menores que 0,3% também resultam em turbulência .
Para analizar o surgimento de espirais e suas caracteristicas utilizamos uma perturbação maior na mesma região (Liquido de Vórtices), o sistema apresenta simetria entre as espirais no gráfico da parte real e também percebemos a presença de defeitos no módulo de (figura 4). Os defeitos, caracterizados pela presença de um ponto nulo ou muito próximo de zero na amplitude, não se anulam mesmo após longos períodos de tempo
Partindo das mesmas condições iniciais anteriores porém na região Vidro de Vórtices, o padrão de espirais muda, a simetria é perdida e em certas regioens podem se expandir formando frozen states. Outra característica é a presença de maior número de células de defeitos. É interessante ressaltar que os pontos defeitos se anulam somente aos pares.
Por fim, na região chamada de Turbulência de Amplitude , à direita da linha AI não encontramos espirais, as células de defeitos não se formam e temos apenas um comportamento caótico no módulo e na fase da Amplitude.
Estados congelados são a solução entre as linhas OR e T representam os vidro de vórtice, a lenta convergência para essa solução é dada pela proximidade da linha T, parâmetros b=-2.0 e c=0.6.
Referências
[1] García-Morales, V., & Krischer, K. (2012). The complex Ginzburg–Landau equation: an introduction. Contemporary Physics, 53(2), 79–95. https://doi.org/10.1080/00107514.2011.642554
[2] H. Riecke, (2021). Methods of Nonlinear Analysis
[3] Igor S. Aranson, Lorenz Kramer, (2001). The World of the Complex Ginzburg-Landau Equation
[4] Cross, M., & Greenside, H. (2009). Pattern Formation and Dynamics in Nonequilibrium Systems. Cambridge University Press.
[5] Hugues Chaté, Paul Manneville (1996). Phase diagram of the two-dimensional complex Ginzburg-Landau equation. Physica A: Statistical Mechanics and its Applications




























































![{\displaystyle x=[40,60]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de037a52a0c4c2716f67f498504471c0e87ad342)
![{\displaystyle y=[40,60]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94223a112efec22caf92562cc6b960f4937555b2)