Método Lax-Friedrich: mudanças entre as edições
Ir para navegação
Ir para pesquisar
Sem resumo de edição |
Sem resumo de edição |
||
| (2 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 3: | Linha 3: | ||
<center><math> | <center><math> | ||
u_i^{n+1}= \frac{1}{2}(u_{i+1}^n + u_{i-1}^n) + \frac{r}{2} (u_{i+1}^n - u_{i-1}^n) | u_i^{n+1}= \frac{1}{2}(u_{i+1}^n + u_{i-1}^n) + \frac{r}{2} (u_{i+1}^n - u_{i-1}^n) | ||
</math></center> | </math></center> | ||
A análise de estabilidade de von Neumann do esquema de Lax resulta na seguinte expressão para o fator de amplificação: | A análise de estabilidade de von Neumann do esquema de Lax resulta na seguinte expressão para o fator de amplificação: | ||
| Linha 9: | Linha 9: | ||
<center><math> | <center><math> | ||
A = \cos(k \Delta x) - ir\sin^2(k \Delta x) | A = \cos(k \Delta x) - ir\sin^2(k \Delta x) | ||
</math></center> | </math></center> | ||
Portanto | Portanto | ||
| Linha 15: | Linha 15: | ||
<center><math> | <center><math> | ||
|A|^2 = 1 - (1-r^2)\sin^2(k \Delta x) | |A|^2 = 1 - (1-r^2)\sin^2(k \Delta x) | ||
</math></center> | </math></center> | ||
Ou seja, o método é incondicionalmente estável para os valores de <math>r</math> menor do que 1. Pela definição de <math>r</math>, temos que: | Ou seja, o método é incondicionalmente estável para os valores de <math>r</math> menor do que 1. Pela definição de <math>r</math>, temos que: | ||
| Linha 21: | Linha 21: | ||
<center><math> | <center><math> | ||
\Delta t < \frac{\Delta x}{v} | \Delta t < \frac{\Delta x}{v} | ||
</math></center> | </math></center> | ||
= Implementação do método = | = Implementação do método = | ||
| Linha 103: | Linha 103: | ||
<center> | <center> | ||
{| | {| | ||
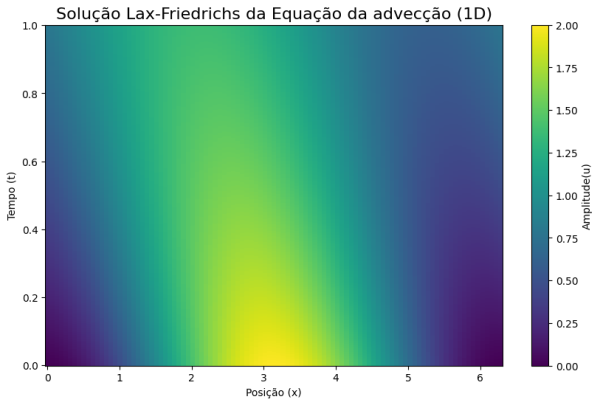
|[[Arquivo: lax-friedrich.png|thumb|upright=0.0|center|Solução pelo método Lax-Friedrich| | |[[Arquivo: lax-friedrich.png|thumb|upright=0.0|center|Solução pelo método Lax-Friedrich|600px]] | ||
|} | |||
</center> | |||
<source lang = "python"> | |||
# Teste: Plota todas as curvas amplitude por posição de todos os tempos: | |||
for tt in range(len(listT-1)): | |||
amplitudes_tt = solv2[ tt,:] | |||
plt.plot(listX, amplitudes_tt) | |||
plt.title('Amplitude em Função da Posição') | |||
plt.xlabel('Posição (x)') | |||
plt.ylabel('Amplitude (u)') | |||
plt.legend() | |||
plt.grid(True) | |||
plt.show() | |||
</source> | |||
<center> | |||
{| | |||
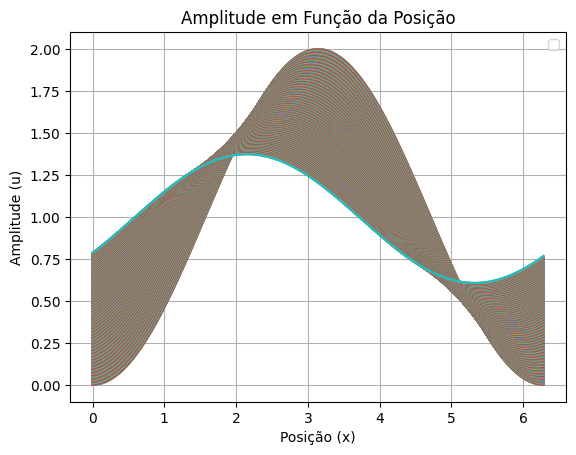
|[[Arquivo: amplitude lax-f.png|thumb|upright=0.0|center|Solução pelo método Lax-Friedrich|600px]] | |||
|} | |} | ||
</center> | </center> | ||
Edição atual tal como às 19h41min de 5 de fevereiro de 2024
A instabilidade no esquema FTCS pode ser corrigida substituindo no lado direito pela média espacial de calculada nos pontos da grade vizinhos. Dessa forma, obtemos:
A análise de estabilidade de von Neumann do esquema de Lax resulta na seguinte expressão para o fator de amplificação:
Portanto
Ou seja, o método é incondicionalmente estável para os valores de menor do que 1. Pela definição de , temos que:
Implementação do método
- Condição inicial: ;
- Condições de contorno para bordas cíclicas.
# Solução pelo método Lax-Friedrichs para equação de advecção
def LaxFad(L, tf, v, Nx, Nt):
"""
Parâmetros:
- L: comprimento
- tf: tempo final
- v: velocidade de propagação
- Nx: número de pontos na direção espacial
- Nt: número de pontos na direção temporal
Retorna:
- Matriz com a solução da equação da onda
"""
dx = L / (Nx - 1)
dt = tf / (Nt - 1)
r = v * dt / dx
u = np.zeros((Nt, Nx+1))
# Condição inicial: u(x,0) = f(x)
x = np.linspace(0, L, Nx+1)
u[0,:] = 1-np.cos(x) # Função que descreve a perturbação da onda
# Condições de contorno borda infinita:
xpos = np.zeros(Nx+1)
xneg = np.zeros(Nx+1)
for i in range(0,Nx+1):
xpos[i] = i+1
xneg[i] = i-1
xpos[Nx] = 0
xneg[0] = Nx
# Iteração no tempo
for n in range(0, Nt - 1):
for i in range(0, Nx+1):
u[n+1,i] = (1/2) * (u[n, int(xpos[i])] + u[n,int(xneg[i])]) + (r/2) * (u[n, int(xpos[i])] - u[n,int(xneg[i])])
return u
# Parâmetros
L = 2*np.pi
tf =1
v = 1 # -1. muda direção de propagação
Nx = 100
Nt = 500
solv2 = LaxFad(L, tf, v, Nx, Nt)
listX = np.linspace(0, L, Nx+1)
listT = np.linspace(0, tf, Nt)
X, T = np.meshgrid(listX, listT)
plt.figure(figsize=(10, 6))
plt.pcolormesh(X, T, solv2, cmap='viridis', shading='auto')
plt.colorbar(label='Amplitude(u)')
plt.xlabel('Posição (x)')
plt.ylabel('Tempo (t)')
plt.title('Solução Lax-Friedrichs da Equação da advecção (1D)', fontsize=16)
plt.show()
# Teste: Plota todas as curvas amplitude por posição de todos os tempos:
for tt in range(len(listT-1)):
amplitudes_tt = solv2[ tt,:]
plt.plot(listX, amplitudes_tt)
plt.title('Amplitude em Função da Posição')
plt.xlabel('Posição (x)')
plt.ylabel('Amplitude (u)')
plt.legend()
plt.grid(True)
plt.show()