Comparação dos métodos numéricos: mudanças entre as edições
Ir para navegação
Ir para pesquisar
(Criou página com '= Gráfico do erro relativo = Como se evidencia nos gráficos que seguem, os métodos implícitos demonstram uma superioridade considerável, apresentando um menor erro relativo em comparação com a solução analítica. Nesse contexto, observamos que o método Crank-Nicholson exibe o menor erro relativo, seguido pelo esquema BTCS e pelo método Lax-Wendroff. <source lang = "python"> def dif(solv0, solv1): erro = np.zeros_like(solv0) for n in range(solv0.sha...') |
|||
| Linha 1: | Linha 1: | ||
= Gráfico do erro relativo = | = Gráfico do erro relativo = | ||
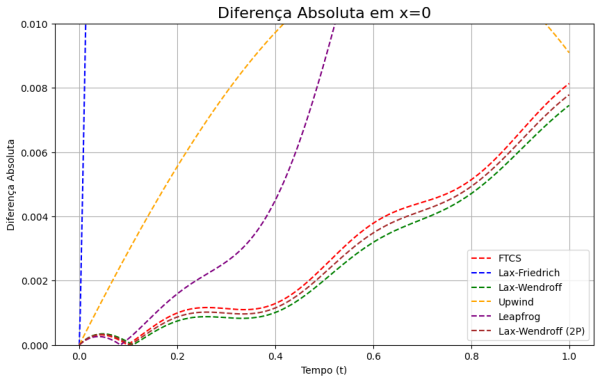
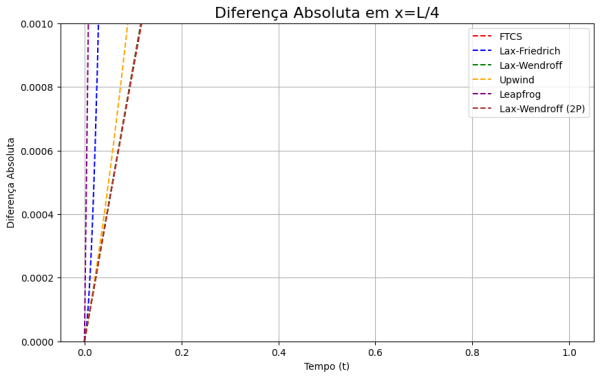
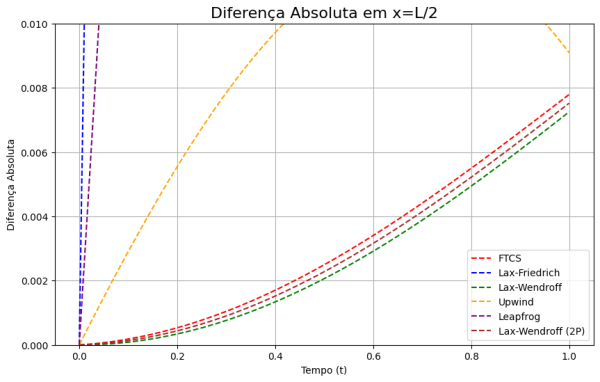
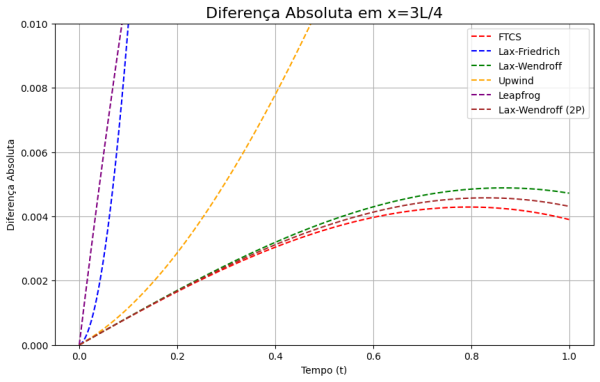
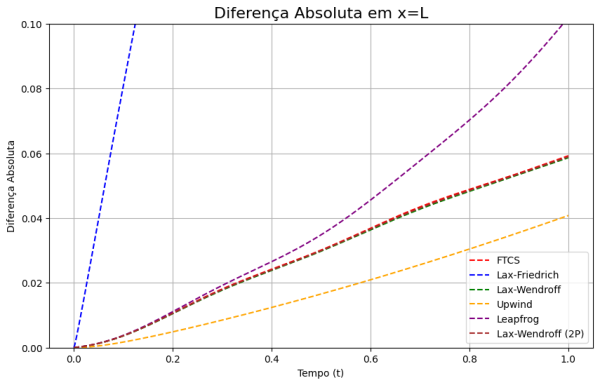
Conforme evidenciado nos gráficos subsequentes, os métodos de Wendroff demonstram uma considerável superioridade, apresentando um menor erro relativo em comparação com a solução analítica. No entanto, é importante observar que tais comparações foram feitas utilizando métodos explícitos de diferenças finitas; outros esquemas seriam possíveis se optássemos por métodos implícitos. | |||
<source lang = "python"> | <source lang = "python"> | ||
Edição atual tal como às 19h28min de 5 de fevereiro de 2024
Gráfico do erro relativo
Conforme evidenciado nos gráficos subsequentes, os métodos de Wendroff demonstram uma considerável superioridade, apresentando um menor erro relativo em comparação com a solução analítica. No entanto, é importante observar que tais comparações foram feitas utilizando métodos explícitos de diferenças finitas; outros esquemas seriam possíveis se optássemos por métodos implícitos.
def dif(solv0, solv1):
erro = np.zeros_like(solv0)
for n in range(solv0.shape[0]):
erro[n, :] = np.abs(solv0[n, :] - solv1[n, :])
return erro
# Calcular a diferença absoluta
erro1 = dif(solv0, solv1)
erro2 = dif(solv0, solv2)
erro3 = dif(solv0, solv3)
erro4 = dif(solv0, solv4)
erro5 = dif(solv0, solv5)
erro6 = dif(solv0, solv6)
plt.figure(figsize=(10, 6))
plt.plot(listT, erro1[:, 0], label='FTCS', color='red', linestyle='--')
plt.plot(listT, erro2[:, 0], label='Lax-Friedrich', color='blue', linestyle='--')
plt.plot(listT, erro3[:, 0], label='Lax-Wendroff', color='green', linestyle='--')
plt.plot(listT, erro4[:, 0], label='Upwind', color='orange', linestyle='--')
plt.plot(listT, erro5[:, 0], label='Leapfrog', color='purple', linestyle='--')
plt.plot(listT, erro6[:, 0], label='Lax-Wendroff (2P)', color='brown', linestyle='--')
plt.grid()
plt.ylim(0,0.01)
plt.xlabel('Tempo (t)')
plt.ylabel('Diferença Absoluta')
plt.title('Diferença Absoluta em x=0', fontsize=16)
plt.legend()
plt.show()
plt.figure(figsize=(10, 6))
x = int(3* Nx / 4)
plt.plot(listT, erro1[:, x], label='FTCS', color='red', linestyle='--')
plt.plot(listT, erro2[:, x], label='Lax-Friedrich', color='blue', linestyle='--')
plt.plot(listT, erro3[:, x], label='Lax-Wendroff', color='green', linestyle='--')
plt.plot(listT, erro4[:, x], label='Upwind', color='orange', linestyle='--')
plt.plot(listT, erro5[:, x], label='Leapfrog', color='purple', linestyle='--')
plt.plot(listT, erro6[:, x], label='Lax-Wendroff (2P)', color='brown', linestyle='--')
plt.grid()
plt.ylim(0,0.001)
plt.xlabel('Tempo (t)')
plt.ylabel('Diferença Absoluta')
plt.title('Diferença Absoluta em x=L/4', fontsize=16)
plt.legend()
plt.show()
plt.figure(figsize=(10, 6))
x = int(Nx / 2)
plt.plot(listT, erro1[:, x], label='FTCS', color='red', linestyle='--')
plt.plot(listT, erro2[:, x], label='Lax-Friedrich', color='blue', linestyle='--')
plt.plot(listT, erro3[:, x], label='Lax-Wendroff', color='green', linestyle='--')
plt.plot(listT, erro4[:, x], label='Upwind', color='orange', linestyle='--')
plt.plot(listT, erro5[:, x], label='Leapfrog', color='purple', linestyle='--')
plt.plot(listT, erro6[:, x], label='Lax-Wendroff (2P)', color='brown', linestyle='--')
plt.grid()
plt.ylim(0,0.01)
plt.xlabel('Tempo (t)')
plt.ylabel('Diferença Absoluta')
plt.title('Diferença Absoluta em x=L/2', fontsize=16)
plt.legend()
plt.show()
plt.figure(figsize=(10, 6))
x = int(3* Nx / 4)
plt.plot(listT, erro1[:, x], label='FTCS', color='red', linestyle='--')
plt.plot(listT, erro2[:, x], label='Lax-Friedrich', color='blue', linestyle='--')
plt.plot(listT, erro3[:, x], label='Lax-Wendroff', color='green', linestyle='--')
plt.plot(listT, erro4[:, x], label='Upwind', color='orange', linestyle='--')
plt.plot(listT, erro5[:, x], label='Leapfrog', color='purple', linestyle='--')
plt.plot(listT, erro6[:, x], label='Lax-Wendroff (2P)', color='brown', linestyle='--')
plt.grid()
plt.ylim(0,0.01)
plt.xlabel('Tempo (t)')
plt.ylabel('Diferença Absoluta')
plt.title('Diferença Absoluta em x=3L/4', fontsize=16)
plt.legend()
plt.show()
plt.figure(figsize=(10, 6))
x = int(Nx)
plt.plot(listT, erro1[:, x], label='FTCS', color='red', linestyle='--')
plt.plot(listT, erro2[:, x], label='Lax-Friedrich', color='blue', linestyle='--')
plt.plot(listT, erro3[:, x], label='Lax-Wendroff', color='green', linestyle='--')
plt.plot(listT, erro4[:, x], label='Upwind', color='orange', linestyle='--')
plt.plot(listT, erro5[:, x], label='Leapfrog', color='purple', linestyle='--')
plt.plot(listT, erro6[:, x], label='Lax-Wendroff (2P)', color='brown', linestyle='--')
plt.grid()
plt.ylim(0,0.1)
plt.xlabel('Tempo (t)')
plt.ylabel('Diferença Absoluta')
plt.title('Diferença Absoluta em x=L', fontsize=16)
plt.legend()
plt.show()