Lennard-Jones e propriedades termodinâmicas: mudanças entre as edições
| Linha 56: | Linha 56: | ||
<center><math>\boldsymbol{v}\left(t+\frac{\Delta t}{2}\right)=\boldsymbol{v}(t)+\frac{1}{2}\boldsymbol{f}(t)\Delta t</math></center> | <center><math>\boldsymbol{v}\left(t+\frac{\Delta t}{2}\right)=\boldsymbol{v}(t)+\frac{1}{2}\boldsymbol{f}(t)\Delta t</math></center> | ||
<center><math>\boldsymbol{r}\left(t+\Delta t\right)=\boldsymbol{r}(t)+\boldsymbol{v}\left(t+\frac{\Delta t}{2}\right)\Delta t</math></center> | <center><math>\boldsymbol{r}\left(t+\Delta t\right)=\boldsymbol{r}(t)+\boldsymbol{v}\left(t+\frac{\Delta t}{2}\right)\Delta t</math></center> | ||
<center><math>\boldsymbol{r}\left(t+\Delta t\right) = \boldsymbol{f}(t+\Delta t | <center><math>\boldsymbol{r}\left(t+\Delta t\right) = \boldsymbol{f}(t+\Delta t)</math></center> | ||
=== Medidas === | === Medidas === | ||
Edição das 16h34min de 17 de abril de 2023
Nesta página apresentamos uma simulação de Dinâmica Molecular utilizando o potencial de Lennard-Jones como potencial de interação entre as partículas.
Potencial de Lennard Jones
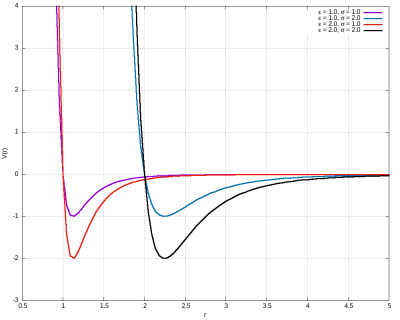
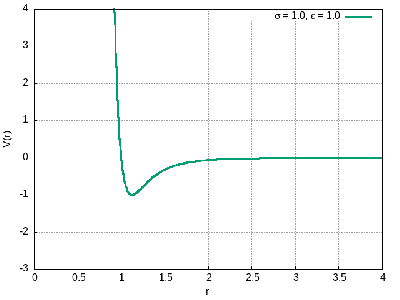
O potencial de Lennard Jones representa a interação entre os àtomos ou moléculas. Possui dois termos distintos: um repulsivo devido às forças de troca do princípio de exclusão de Pauli (origem quântica) e um atrativo devido às forças de van der Walls.
O termo proporcional à Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{r^{6}}} é o termo atrativo, enquanto o termo proporcional à Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{r^{12}}} é o termo repulsivo, muito mais intenso à curtas distâncias. A constante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} descreve a profundidade do poço deste potencial, enquanto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} descreve a posição do ponto de equilíbrio estável. Nas imagens abaixo, podemos ver o comportamento do potencial para diferentes valores de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} .
 Comportamento do potencial de Lennard-Jones para diferentes valores de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon}
e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma}
. |
A força que uma partícula sofre, quando sujeita a este potencial é dada por
Dinâmica Molecular
A abordagem da dinâmica molecular se baseia em integrar as equações de movimento newtonianas para todas as partículas do sistema. Abaixo, podemos sintetizar um resumo dos passos para realizar uma simulação de dinâmica molecular.
1. Inicializar a posição e velocidade das partículas do sistema.
2. Calcular as forças de interação entre todas as partículas do sistema.
3. Integrar as equações de movimento utilizando algum algoritmo integrador.
4. Medir grandezas físicas, como energia cinética, energia potencial, temperatura e pressão.
A seguir, vamos explicitar cada um dos passos.
Inicialização
O primeiro passo é inicializar a posição inicial das partículas. Podemos iniciar a simulação com as partículas distribuídas em qualquer forma que desejarmos, entretanto a forma mais comum de arranjar as partículas é em um formato cúbico ou em um formato triangular. O formato triangular é mais denso do que o formato cúbico. Além disso, a densidade calculada em uma simulação é a densidade numérica, ou seja, quanto de área, ou volume se for em três dimensões, da caixa está ocupada. Esta densidade é calculada como a soma da área ocupada por cada partícula dividida pela area total da caixa. É importante mencionar que as partículas são pontuais, entretanto como o Potencial de Lennard-Jones tende à infinito quanto a distância entre as partículas diminui, cada partícula é como se tivesse um raio efetivo, na qual outra partícula não consegue atravessar. É como se partículas fossem esferas que sofrem colisões umas com as outras. Além disso, podemos inicializar a velocidade das partículas de diferentes formas.
a) Velocidade nula:
Se dermos velocidade nula para todas as partículas, a simulação vai demorar mais, uma vez que elas começarão o movimento somente devido à distância de interação entre elas. Se elas estiverem muito afastadas, a força entre elas será muito pequena e demorará muito para que o sistema comece a evoluir e equilibrar, que é o nosso objetivo.
b) Velocidade aleatória:
A opção mais utilizada. Ao iniciarmos as velocidades de forma aleatória, as partículas não demoram tanto para interagir e conseguimos identificar a parte não-equilibrada e a equilibrada do sistema.
c) Distribuição de Maxwell-Boltzmann de velocidades:
Já esperamos que quando o sistema for equilibrar, a distribuição de velocidades das partículas seja a distribuição de Maxwell-Boltzman. Iniciar as velocidades desta forma acelera a simulação de forma significativa, entretanto se você tem algum interesse no sistema antes dele entrar em equilíbrio, você perderá informações sobre.
Cálculo das forças
Esta etapa é a mais custosa do ponto de vista computacional, uma vez que temos que calcular a força sofrida por cada partícula do sistema devido à todas as outras N-1 partículas, e com isso precisamos computar N(N-1) forças. Entretanto, se a interação exercida em i por j for a mesma que a exercida em j por i, então este número cai pela metade. Ainda é possível reduzir o tempo e o gasto computacional se considerarmos apenas as partículas dentro de um "raio crítico" Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_c} . Este raio crítico é geralmente tomado como metade do tamanho da caixa. Em nossa simulação, contabilizamos todas as interações.
Integração das equações de movimento
Uma vez que nós obtemos a força sofrida por cada partícula, estamos preparados para integrar as equações de movimento. Para isso, precisamos escolher algum integrador que atenda à nossas necessidades. O integrador mais adequado aos nossos propósitos é um algoritmo do tipo Verlet. Em particular, utilizamos em nossa simulação o algoritmo de Velocity-Verlet.
Medidas
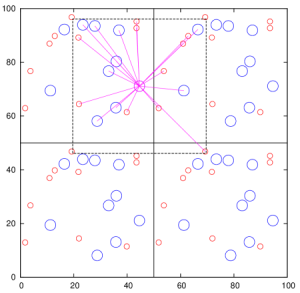
Convenção da imagem mímina e PBC
Existem algumas características que devem ser levadas em consideração quando fazemos uma simulação de dinâmica molecular. Como integrar as equações de movimento requer um poder computacional elevado para muitas partículas, fazemos uma simulação de um "pedaço" do sistema de interesse. Construímos este "pedaço" como uma caixa de lado L e confinamos nossas partículas neste espaço. O número de partículas permanecesse constante e quando uma partícula atravessa a fronteira da caixa, ela retorna do outro lado. Isso simula um sistema infinito. Esta condição de contorno é chamada de condição de contorno periódica (Periodic Boundary Condition - PBC).
Outra característica importante é a convenção da imagem mínima. Esta característica diz respeito à interação entre as partículas. Como cada partícula interage com todas as outras, se a distância entre as partículas for maior do que a metade da caixa, ou seja, L/2, então devemos imaginar que ela vai interagir com a partícula correspondente na caixa "ao lado". Isso é uma extensão do conceito de sistema infinito discutido anteriormente. Ao lado temos uma figura que esquematiza este conceito.
Simulação
Nesta simulação, utilizamos L = 25 e N = 108, onde N é o número de partículas. Neste contexto, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = 0.724}
Bibliografia
D. Frenkel, B. Smit. Understanding Molecular Simulation: From Algorithms to Applications. Academic Press. 2002.