Shooting method e Método de Crank-Nicolson: mudanças entre as edições
| (15 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 55: | Linha 55: | ||
<center><math>E_n=\frac{\hbar^2k_n^2}{2m}=\frac{n^2\pi^2\hbar^2}{2mL^2}.</math></center> | <center><math>E_n=\frac{\hbar^2k_n^2}{2m}=\frac{n^2\pi^2\hbar^2}{2mL^2}.</math></center> | ||
Utilizando a equação acima, pode-se calcular os valores da energia de cada estado estacionário. Para o caso de um elétron, as energias referentes aos três estados estacionários são <math>E_1=0,376</math> eV, <math>E_2=1,504</math> eV e <math>E_3=3,384</math> eV. | Utilizando a equação acima, pode-se calcular os valores da energia de cada estado estacionário. Para o caso de um elétron num poço hipotético de 1m, as energias referentes aos três estados estacionários são <math>E_1=0,376</math> eV, <math>E_2=1,504</math> eV e <math>E_3=3,384</math> eV. | ||
Na próxima seção será feita uma estimativa dos valores acima expostos através do "Shooting method". | Na próxima seção será feita uma estimativa dos valores acima expostos através do "Shooting method". | ||
| Linha 87: | Linha 87: | ||
Com a discretização acima, foi possível implementar o algoritmo. Das condições de contorno do problema, sabe-se que <math>\psi(0)=0</math>, de modo que <math>\psi_1=0</math>. No entanto, o valor da derivada <math>\dot{\psi_1}</math> não é conhecido, de modo que supõe-se que seja uma constante, a saber, <math>\dot{\psi_1}=1</math>. Chutando que <math>E=0</math>, utilizando a massa do elétron e <math>L=1</math>, obtém-se a primeira solução estacionária: | Com a discretização acima, foi possível implementar o algoritmo. Das condições de contorno do problema, sabe-se que <math>\psi(0)=0</math>, de modo que <math>\psi_1=0</math>. No entanto, o valor da derivada <math>\dot{\psi_1}</math> não é conhecido, de modo que supõe-se que seja uma constante, a saber, <math>\dot{\psi_1}=1</math>. Chutando que <math>E=0</math>, utilizando a massa do elétron e <math>L=1</math>, obtém-se a primeira solução estacionária: | ||
[[Arquivo:n=1.png|300px|thumb|center|Solução estacionária (n=1)]] | [[Arquivo:n=1.png|300px|thumb|center|Solução estacionária (n=1)]] | ||
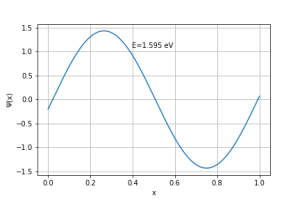
Pode-se observar que o valor de energia obtido numericamente é cerca de | Pode-se observar que o valor de energia obtido numericamente é cerca de 2% menor do que aquele obtido analiticamente. | ||
Para o caso n=2: | Para o caso n=2: | ||
| Linha 151: | Linha 151: | ||
<center><math>\Psi_{j}^{n+1}b_{j}+\Psi_{j-1}^{n+1}a+\Psi_{j+1}^{n+1}a = \Psi_{j}^{n}b_{j}^{*}+\Psi_{j-1}^{n}a^{*}+\Psi_{j+1}^{n}a^{*} .</math></center> | <center><math>\Psi_{j}^{n+1}b_{j}+\Psi_{j-1}^{n+1}a+\Psi_{j+1}^{n+1}a = \Psi_{j}^{n}b_{j}^{*}+\Psi_{j-1}^{n}a^{*}+\Psi_{j+1}^{n}a^{*} .</math></center> | ||
A equação acima pode ser escrita em forma matricial, de modo que: | |||
<center><math>\hat{C}\Psi^{n+1}=\hat{D}\Psi^{n},</math></center> | |||
onde | |||
<center><math> | |||
\hat{C} = | |||
\begin{bmatrix} | |||
b _{0} &a &0 & &... &0 \\ | |||
a & b_{1} &a &0 &... &0\\ | |||
0 & a &b_{2} &a & 0 &0 \\ | |||
0 & 0 & \ddots & \ddots &\ddots \\ | |||
... & ... &... & a &b_{j-1} &a \\ | |||
0 & 0 &... & 0 &a &b_{j}\\ | |||
\end{bmatrix} | |||
</math></center> | |||
e | |||
<center><math> | |||
\hat{D} = | |||
\begin{bmatrix} | |||
b_{0}^{*} &a &0 & &... &0 \\ | |||
a^{*} & b_{1}^{*} &a^{*} &0 &... &0\\ | |||
0 & a^{*} &b_{2}^{*} &a^{*} & 0 &0 \\ | |||
0 & 0 & \ddots & \ddots &\ddots \\ | |||
... &... &... & a^{*} &b_{j-1}^{*} &a^{*} \\ | |||
0 & 0 &... & 0 &a^{*} &b_{j}^{*}\\ | |||
\end{bmatrix} | |||
</math></center> | |||
Para avaliar a evolução temporal do sistema, é necessário encontrar <math>\Psi^{n+1}</math>. Utilizando resultados anteriores, pode-se obter <math>\Psi^{n+1}</math> através da seguinte relação: | |||
<center><math> | |||
\Psi^{n+1}=\hat{C}^{-1}\hat{C^{*}}\Psi^{n} | |||
</math></center> | |||
===Poço de potencial infinito=== | |||
Para o presente caso a ideia é obter a evolução temporal do sistema, impondo condições de contorno iguais a zero, de modo que os operadores <math>\hat{C}</math> e <math>\hat{D}</math> ficam: | |||
<center><math> | |||
\hat{C} = | |||
\begin{bmatrix} | |||
1 &0 &0 & &... &0 \\ | |||
a & b &a &0 &... &0\\ | |||
0 & a &b &a & 0 &0 \\ | |||
0 & 0 & \ddots & \ddots &\ddots \\ | |||
... &... &... & a &b &a \\ | |||
0 & 0 &... & 0 &0 &1\\ | |||
\end{bmatrix} | |||
</math></center> | |||
e | |||
<center><math> | |||
\hat{D} = | |||
\begin{bmatrix} | |||
1 &0 &0 & &... &0 \\ | |||
a^{*} & b^{*} &a^{*} &0 &0... &0\\ | |||
0 & a^{*} &b^{*} &a^{*} & 0 &0 \\ | |||
0 & 0 & \ddots & \ddots &\ddots \\ | |||
... &... &... & a^{*} &b^{*} &a^{*} \\ | |||
0 & 0 &... & 0 &0 &1\\ | |||
\end{bmatrix} | |||
</math></center> | |||
A ideia é que o primeiro e o último termo do tanto do vetor <math>\Psi^{n}</math> quanto do vetor <math>\Psi^{n+1}</math> seja constante, o que satisfaz as condições de contorno do presente caso. Também é interessante notar que os índices <math>b</math> são todos constantes, visto que no presente caso o potencial dentro do poço é nulo. | |||
Implementando o algoritmo descrito acima, obteve-se: | |||
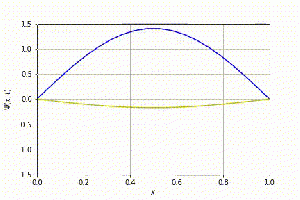
[[Arquivo:Animação_n_1.gif|300px|thumb|center|Evolução temporal (n=1)]] | |||
Evolução temporal para o caso n=1. Nesta animação e nas subsequentes, foram sobrepostas as partes real e imaginária da equação de Schrödinger: a linha azul diz respeito à parte real enquanto a amarela, à imaginária. | |||
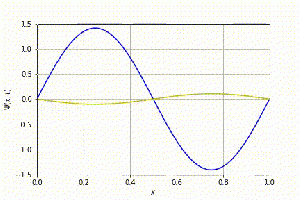
[[Arquivo:Animação_n_2.gif|300px|thumb|center|Evolução temporal (n=2)]] | |||
Na figura acima, tem-se a evolução do caso n=2. | |||
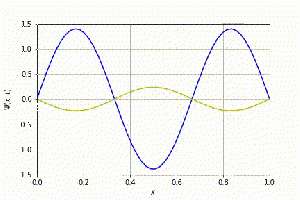
[[Arquivo:Animação_n_3.gif|300px|thumb|center|Evolução temporal (n=3)]] | |||
Por último, o caso n=3. | |||
==Códigos== | |||
[[ Crank-Nicolson (Poço de potencial infinito) ]] | |||
[[ Shooting method (Poço de potencial infinito) ]] | |||
== Referências == | |||
Griffiths, David J. '''Introduction to Quantum Mechanics'''. Pearson Prentice Hall, 2ª ed. 2005. | |||
Giordano, N. J. Nakanishi, H. '''Computational Physics'''. Pearson Prentice Hall, 2ª ed. 2006. | |||
Scherer, C. '''Métodos Computacionais da Física'''. Livraria da Física, 2ª ed. 2010. | |||
Edição atual tal como às 22h59min de 13 de fevereiro de 2023
O objetivo deste trabalho é aplicar o Shooting method (método do chute) para encontrar as primeiras funções de onda espaciais da Equação de Schrödinger para o caso do poço de potencial infinito. Após, será realizada a evolução temporal através do Método de Crank-Nicolson.
Equação de Schrödinger
A equação de Schrödinger unidimensional pode ser escrita da seguinte maneira:
Para resolvê-la é necessário efetuar uma separação de variáveis:
Aplicando na primeira equação e separando os termos espaciais dos termos temporais, chega-se a uma equação com o seguinte formato:
Pelo fato da parte da esquerda ser dependente de t e a parte da direita ser dependente de x e de ambas estarem relacionadas por uma igualdade, é necessário que ambos os lados sejam constantes: em outras palavras, não é possível modificar um lado sem necessariamente alterar o outro. Através de um raciocínio perspicaz, a constante em questão será denominada E.
Parte temporal
A parte que diz respeito à evolução temporal:
A solução geral possui o seguinte formato
cuja constante C pode, neste caso, ser absorvida, de modo que
Parte espacial
Quanto à parte espacial, utilizando o mesmo raciocínio empregado anteriormente, a equação pode ser escrita como
Para este caso, no entanto, não há uma única solução, pois esta depende do potencial V escolhido. Para o presente trabalho optou-se por trabalhar com o caso do poço infinito de potencial pelo fato das soluções analíticas já serem conhecidas, de modo a tornar possível avaliar os resultados numéricos obtidos à luz da solução analítica.
Poço de potencial infinito
Esquematicamente, tem-se:
O potencial pode ser descrito como:
Dentro do poço, onde $V=0$, o problema pode ser modelado da seguinte maneira
ou
onde
A solução é dada por
Aplicando as condições de contorno e efetuando a normalização da função de onda, obtém-se a solução geral
cujas energias discretizadas são
Utilizando a equação acima, pode-se calcular os valores da energia de cada estado estacionário. Para o caso de um elétron num poço hipotético de 1m, as energias referentes aos três estados estacionários são eV, eV e eV.
Na próxima seção será feita uma estimativa dos valores acima expostos através do "Shooting method".
Shooting Method
Muitos métodos numéricos (e.g. Runge-Kutta, Forward Euler) requerem os valores da função e de sua derivada no ponto inicial. Acontece que podem haver problemas em que estes valores não estarão disponíveis, principalmente o valor da derivada em questão. Uma alternativa seria conjecturar o valor da condição inicial e integrar, através de um método apropriado, em direção à outra condição de contorno: um "chute" apropriado faria com que a integração evoluísse e retornasse um valor muito próximo, a depender da acurácia necessária, ao da condição de contorno. A ideia seria executar os seguintes passos:
- Supor um valor para a condição de contorno desconhecida (e.g. ou );
- Integrar o problema através de um método conhecido até a próxima condição de contorno (e.g., );
- Se o chute inicial não fez com que o sistema evoluísse até , então deve-se supor outro valor para a condição inicial e repetir o procedimento.
O método descrito acima de forma simplificada recebe o nome, em inglês, de Shooting method, o que em português seria algo como "Método do tiro" ou "Método do chute". Na próxima seção esse método será aplicado para o caso do poço infinito de potencial.
Poço de potencial infinito
Seja a equação , onde .
Escrevendo com outra notação: .
Dividindo o problema em 's pequenos, pode-se reescrever a equação acima da seguinte forma:
.
Também:
.
Além disso:
.
A integração, então, é realizada utilizando as relações 8, 9, 10 e 11, até que se atinja a borda do poço, isto é, .
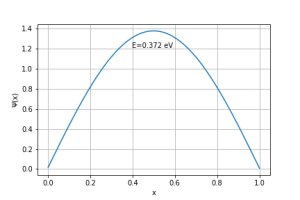
Com a discretização acima, foi possível implementar o algoritmo. Das condições de contorno do problema, sabe-se que , de modo que . No entanto, o valor da derivada não é conhecido, de modo que supõe-se que seja uma constante, a saber, . Chutando que , utilizando a massa do elétron e , obtém-se a primeira solução estacionária:
Pode-se observar que o valor de energia obtido numericamente é cerca de 2% menor do que aquele obtido analiticamente.
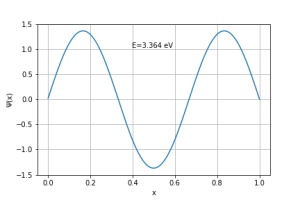
Para o caso n=2:
Aqui, o valor obtido numericamente é aproximadamente 5% maior do que o valor obtido analiticamente.
Para o caso n=3:
Para este caso, o valor numérico é cerca de 1% menor do que o valor analítico.
Método de Crank-Nicolson
Seja a equação diferencial
,
onde é um operador diferencial linear em r.
Em forma discretizada no tempo, pode-se escrever
.
Por simetria, pode-se escrever a equação acima utilizando um f à direita:
A equação acima é dita "explícita" pois, para o cálculo de , só é utilizado o valor já explicitamente calculado . Já a equação anterior é chamada implícita pois está presente explicitamente. Em termos numéricos, um método peca pelo excesso enquanto o outro o faz pela falta, de modo que um resultado mais satisfatório pode ser obtido ao tomar-se a média dos dois:
Após alguma álgebra:
.
Chamando e , onde I indica a matriz identidade, pode-se reescrever a equação acima na seguinte maneira:
.
Trata-se do método de Crank-Nicolson, mais estável e preciso do que os métodos implícito e explícito. Caso o problema apresentar condições de contorno, estas serão devidamente implementadas nos elementos das matrizes M e E.
Equação de Schrödinger
Seja a equação de Schrödinger unidimensional
.
Efetuando a discretização das variáveis através do Método de Crank-Nicolson, obtém-se:
Substituindo as discretizações na eq. de Schrödinger:
Supondo e separando as partes explícita e implícita, obtém-se, após alguma álgebra:
Definindo
e
obtém-se:
A equação acima pode ser escrita em forma matricial, de modo que:
onde
e
Para avaliar a evolução temporal do sistema, é necessário encontrar . Utilizando resultados anteriores, pode-se obter através da seguinte relação:
Poço de potencial infinito
Para o presente caso a ideia é obter a evolução temporal do sistema, impondo condições de contorno iguais a zero, de modo que os operadores e ficam:
e
A ideia é que o primeiro e o último termo do tanto do vetor quanto do vetor seja constante, o que satisfaz as condições de contorno do presente caso. Também é interessante notar que os índices são todos constantes, visto que no presente caso o potencial dentro do poço é nulo.
Implementando o algoritmo descrito acima, obteve-se:
Evolução temporal para o caso n=1. Nesta animação e nas subsequentes, foram sobrepostas as partes real e imaginária da equação de Schrödinger: a linha azul diz respeito à parte real enquanto a amarela, à imaginária.
Na figura acima, tem-se a evolução do caso n=2.
Por último, o caso n=3.
Códigos
Crank-Nicolson (Poço de potencial infinito)
Shooting method (Poço de potencial infinito)
Referências
Griffiths, David J. Introduction to Quantum Mechanics. Pearson Prentice Hall, 2ª ed. 2005.
Giordano, N. J. Nakanishi, H. Computational Physics. Pearson Prentice Hall, 2ª ed. 2006.
Scherer, C. Métodos Computacionais da Física. Livraria da Física, 2ª ed. 2010.

















































![{\displaystyle {\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}\Psi }{\partial x^{2}}}={\frac {\hbar ^{2}}{2m}}\left[{\frac {(\Psi _{j+1}^{n+1}-2\Psi _{j}^{n+1}+\Psi _{j-1}^{n+1})+(\Psi _{j+1}^{n}-2\Psi _{j}^{n}+\Psi _{j-1}^{n})}{2\Delta x^{2}}}\right];}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7c968ac3ad9989d7d15e2e9a8072c1ede3bbb71)
![{\displaystyle V\Psi ={\frac {1}{2}}[V_{j}^{n+1}\Psi _{j}^{n+1}+V_{j}^{n}\Psi _{j}^{n}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30a5b216a7db3469085592add03480b7c8e91b1b)
![{\displaystyle i\left({\frac {\Psi _{j}^{n+1}-\Psi _{j}^{n}}{\Delta t}}\right)=-{\frac {\hbar ^{2}}{4m(\Delta x)^{2}}}\left[(\Psi _{j+1}^{n+1}-2\Psi _{j}^{n+1}+\Psi _{j-1}^{n+1})+(\Psi _{j+1}^{n}-2\Psi _{j}^{n}+\Psi _{j-1}^{n})\right]+{\frac {1}{2}}[V_{j}^{n+1}\Psi _{j}^{n+1}+V_{j}^{n}\Psi _{j}^{n}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8d6a69db036035dd3dc44b8037fb5c1f75bacdd)

![{\displaystyle \Psi _{j}^{n+1}\left[1+{\frac {i\Delta t}{2}}\left({\frac {1}{\Delta x^{2}}}+V_{j}^{n+1}\right)\right]+\Psi _{j-1}^{n+1}\left[-{\frac {i\Delta t}{4\Delta x^{2}}}\right]+\Psi _{j+1}^{n+1}\left[-{\frac {i\Delta t}{4\Delta x^{2}}}\right]=\Psi _{j}^{n}\left[1-{\frac {i\Delta t}{2}}\left({\frac {1}{\Delta x^{2}}}+V_{j}^{n}\right)\right]+\Psi _{j-1}^{n}\left[-{\frac {i\Delta t}{4\Delta x^{2}}}\right]+\Psi _{j+1}^{n}\left[{\frac {i\Delta t}{4\Delta x^{2}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf2404174881eb0d7e902aed7d2f2b0bdeef3957)