Potencial de Lennard-Jones: mudanças entre as edições

De Física Computacional
Ir para navegação Ir para pesquisar
Linha 80: Linha 80:
|-
|-
|}
|}
Olhando para os gráficos de enrgia podemos notar uma grande diferença entre temperaturas e densidades. Claramente quanto maior a temperatura, maior a energia, o que é esperado. Além disso quando maior a temperatura, aparentemente há uma meio vairiabilidade na energia, o que também é esperado, pois a temperatura maior, faz com que mais moviementos desfavoráveis (dU >0) sejam aceitos.
Olhando para a densidade, fica claro, que quanto maior a densidade, menor a energia. Para densidade 0.1 e temperaturas baixas (0.5 e 1.5), a energia chega até a ficar positiva em alguns pontos, logo voltando a ficar zero ou menor. Isso provavelmente acontece, pois com menos densidade, os movimentos tendem a não cair pŕoximos do minimo do potencial de uma partícula. Na verdade, como há muito espaço livre, tendem a ficar mais afastados, o que fa com que as vezes possam ficar a uma distancia de <math>\approx 0.75</math> de uma partícula (e não 0.56 como esperado). Assim é mais provável que possam dar saltos próximos do centro (para 0.4, por exemplo) e aumentar muito a energia do sistema.


== Transição de fase ==
== Transição de fase ==
Linha 103: Linha 107:
|-
|-
|}
|}
Olhando para a posição das partículas, podemos ver claramente uma transição de fase.


= Código =
= Código =

Edição das 12h44min de 19 de outubro de 2022

Nome: André Bracht Burmeister

Fluidos estão em todos os lugares e, portanto, estudá-los é muito importante. Como são objetos de estudo extremamente complicados, se fazem necessários modelos e simplificações. Uma simplificação muito usada é a análise do sistema em duas dimensões apenas, excluindo a terceira dimensão espacial.


O Modelo

Um fluido bidimensional pode ser modelado como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} partículas em um plano com densidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho} (partículas por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma^2} ). O plano é um quadrado de lado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = \sqrt{\frac{N}{\rho}}} . Para escolher a posição inicial de uma partícula, são escolhidas coordenadas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} aleatórias entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} .

O Método de Monte Carlo

Para evoluir o sistema, usaremos caminhadas aletórias, escolhendo as partículas com o método de Monte Carlo[[1]]. O método de Monte Carlo consiste em escolher uma partícula aleatoriamente entre as Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} . Então escolhemos aleatoriamente um deslocamento proposto para a partícula Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{dL} = d\vec{x} + d\vec{y} } , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dx} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dy} estão entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dL_{max}} . A partícula só é realmente deslocada em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{dL}} de acordo com o Algoritmo de Metropolis-Hasting.

Algoritmo de Metropolis-Hasting

O Algoritmo de Metropolis-Hasting consiste em escolher se o movimento será ou não aceito usando a diferença de energia potencial entre o estado após o movimento e anterior ao movimento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dU = U(r_2) - U(r_1)} . A probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(dU)} de aceitar o movimento é dada por: 

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(dU) = min{(1,  e^{-\beta dU} )}}

Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = \frac{1}{T \cdot k_B}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} é a temperatura e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B} é a constante de Boltzmann.

O Potencial de Lennard Jones

Para que o algoritmo funcione, precisamos então encontrar uma maneira de calcular a energia potencial de cada partícula. O potencial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U'} que uma partícula causa na outra, pode ser aproximado a uma distribuição em termos da distância Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r'} entre elas: 

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U'(r') = 4 \epsilon \left [ \left ( \frac{\sigma}{r'} \right )^{12} - \left ( \frac{\sigma}{r'} \right )^{6} \right ]}

Esse potencial é conhecido como o potencial de Lennard-Jones, primeiro apresentado por ele em seu artigo [1].

Unidades Reduzidas

Configuração de menor energia entre três partículas. Os círculos têm raio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^{-5/6}\sigma} , metade da distância de menor potencial.

Ao realizar a simulação computacionalmente, usar unidades do sistema internacional faria com que os números ficassem muito grandes ou muito pequenos, fazendo com que perdêssemos em precisão. Portanto, faz sentido que usemos unidades reduzidas em termos de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} e a constante de Boltzmann Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{B} } . As unidades utilizadas foram:

Grandeza Comprimento Temperatura Energia Densidade
Unidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon/k_B} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 / \sigma^{3}}

Usando as novas unidades o potencial de Lennard-Jones fica: 

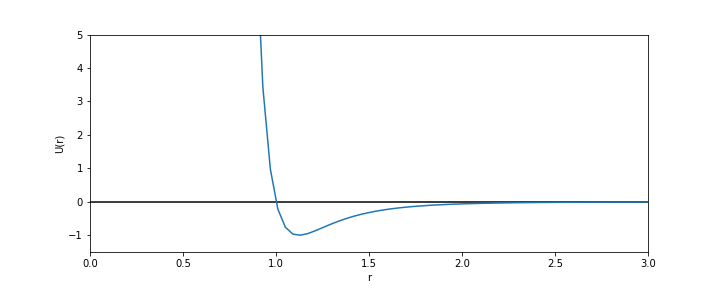
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(r) = 4  \left [ \left ( \frac{1}{r} \right )^{12} - \left ( \frac{1}{r} \right )^{6} \right ]}

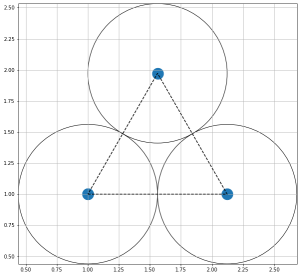
O formato do potencial faz com que para distâncias grandes, a interação entre partículas seja muito pequena e, para distâncias muito pequenas, haja uma força de repulsão que tende ao infinito. Além disso, a região de potencial mínimo se encontra a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^{1/6}\sigma \approx 1.12\sigma } do centro da partícula. Ou seja, as partículas tendem a se organizar em uma configuração similar a da figura à direita, onde o raio dos círculos é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2^{1/6}\sigma}{2} = 2^{-5/6}\sigma \approx 0.56}

Potencial de Lennard-Jones com unidades reduzidas
Potencial lennard jones.png

Escolha de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dL_{max}}

Foi escolhido um deslocamento máximo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dL_{max} = \frac{2^{1/6}}{2} = 2^{-5/6}} , pois isso faz com que o deslocamento não seja maior que metade da distância ao mínimo do potencial.

Resultados

A simulação foi rodada com 32 partículas, para temperaturas de 0.1, 0.3, 0.5 e 1.5 e densidades de 0.1, 0.5 e 0.9 e com 1000 MCS. Onde 1 MCS (monte carlo step) é o número de passos correspondente ao número de partículas (nesse caso, 1 MCS = 32 passos).

Energia

Medidas de energia Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} a cada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle MCS} para diferentes densidades e temperaturas
Energy graph T1.5 N32 d0.1 MCS10000 dL 0.561.png
Energy graph T1.5 N32 d0.5 MCS10000 dL 0.561.png
Energy graph T1.5 N32 d0.9 MCS10000 dL 0.561.png

Olhando para os gráficos de enrgia podemos notar uma grande diferença entre temperaturas e densidades. Claramente quanto maior a temperatura, maior a energia, o que é esperado. Além disso quando maior a temperatura, aparentemente há uma meio vairiabilidade na energia, o que também é esperado, pois a temperatura maior, faz com que mais moviementos desfavoráveis (dU >0) sejam aceitos.

Olhando para a densidade, fica claro, que quanto maior a densidade, menor a energia. Para densidade 0.1 e temperaturas baixas (0.5 e 1.5), a energia chega até a ficar positiva em alguns pontos, logo voltando a ficar zero ou menor. Isso provavelmente acontece, pois com menos densidade, os movimentos tendem a não cair pŕoximos do minimo do potencial de uma partícula. Na verdade, como há muito espaço livre, tendem a ficar mais afastados, o que fa com que as vezes possam ficar a uma distancia de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx 0.75} de uma partícula (e não 0.56 como esperado). Assim é mais provável que possam dar saltos próximos do centro (para 0.4, por exemplo) e aumentar muito a energia do sistema.

Transição de fase

Posição das partículas ao fim da simulação com diferentes densidades e temperaturas
First last positions T0.1 N32 d0.1 MCS10000 dL 0.561.png
First last positions T0.1 N32 d0.5 MCS10000 dL 0.561.png
First last positions T0.1 N32 d0.9 MCS10000 dL 0.561.png
First last positions T0.3 N32 d0.1 MCS10000 dL 0.561.png
First last positions T0.3 N32 d0.5 MCS10000 dL 0.561.png
First last positions T0.3 N32 d0.9 MCS10000 dL 0.561.png
First last positions T0.5 N32 d0.1 MCS10000 dL 0.561.png
First last positions T0.5 N32 d0.5 MCS10000 dL 0.561.png
First last positions T0.5 N32 d0.9 MCS10000 dL 0.561.png
First last positions T1.5 N32 d0.1 MCS10000 dL 0.561.png
First last positions T1.5 N32 d0.5 MCS10000 dL 0.561.png
First last positions T1.5 N32 d0.9 MCS10000 dL 0.561.png

Olhando para a posição das partículas, podemos ver claramente uma transição de fase.

Código

"""lennard_jones.ipynb

Automatically generated by Colaboratory.

Original file is located at
    https://colab.research.google.com/drive/1jSPjBz0RXXWLEAzf3zcHgdlQpzjyO_ni

# Potencial de Lennard-Jones
# Monte Carlo no contínuo

#### Delete variables and import packages
"""

import numpy as np
from matplotlib import pyplot as plt
from matplotlib.animation import FuncAnimation 
import random
from scipy.optimize import bisect as find_root

"""## Simulação:

### Definições Numéricas:
"""

densidade = 0.1 #(2 ** (2/3)) * (3 ** (-1/2))  # partícula(s) por sigma^2 (partículas por área)
densidade_round = round(densidade, 2)
n_particles = 64
L = np.sqrt(n_particles / densidade)  # unidade de sigma
print(L)
dLmax = 0.1
MCS = 10000
eps = 1
T = .1
k = 1
beta = 1/(k*T)
raio = 2**(-5/6)

"""### Funcões:"""

def lennard_jones(r1, r2, L):  # r1 e r2 em unidades de sigma (na vdd seria r1/sig e r2/sig)
    dr = np.absolute(np.subtract(r2, r1))
    for i in np.arange(2):
        if dr[i] > 0.5:
            dr[i] = L - dr[i]

    r2 = (dr[0] ** 2) + (dr[1] ** 2)
    sr2 = 1/r2
    return 4 * (((sr2) ** 6) - ((sr2) ** 3))


def initial_energy(pos_particles, n_particles, L):
    U0 = 0
    for xxx in range(n_particles - 1):
        for yyy in range(xxx+1, n_particles):
            U0 += lennard_jones(pos_particles[:, xxx], pos_particles[:, yyy], L=L)
    return U0


def energy_var(p, pos_particles, n_particles, L, new_pos=np.zeros(2)):
    U1 = 0
    U2 = 0
    for i in range(n_particles - 1):
        j = (i + p + 1) % n_particles  # j vai ser todas as partículas 
        # exceto a partícula p (porque p interage com todas, menos com ela mesma)
        U1 += lennard_jones(pos_particles[:, j], pos_particles[:, p], L=L)
        U2 += lennard_jones(pos_particles[:, j], new_pos, L=L)
    return U2 - U1


def main_loop(dLmax, beta, n_particles, MCS, L, acceptance_array=False, 
              last_acceptance=False):
    
    pos_particles = L * np.random.random([2, n_particles])
    # Random positions:
    pos_MCS = np.zeros([MCS+1, 2, n_particles])
    pos_particles = pos_particles
    pos_MCS[0] = pos_particles

    # Energy:
    energy_arr = np.zeros(MCS+1)
    energy = initial_energy(pos_particles, n_particles, L=L)
    energy_arr[0] = energy

    # Acceptance:
    accepted = 0
    if acceptance_array:
        acceptance_arr = np.zeros(MCS)

    # Main Loop:
    for m in range(MCS):
        for _ in range(n_particles):
            p = random.randint(0, n_particles - 1)
            # change position:
            displacement = dLmax * ((2 * np.random.random([2])) - 1)
            new_pos = pos_particles[:, p] + displacement
            for i in range(2):
                if new_pos[i] < 0:
                    new_pos[i] += L
                elif new_pos[i] > L:
                    new_pos[i] -= L 
            dU = energy_var(p, pos_particles, n_particles, L, new_pos)
            if dU <= 0:
                pos_particles[0][p] = new_pos[0]
                pos_particles[1][p] = new_pos[1]
                energy += dU
                accepted += 1
            else:
                if random.random() < np.exp(-beta * dU):
                    pos_particles[0][p] = new_pos[0]
                    pos_particles[1][p] = new_pos[1]
                    energy += dU
                    accepted += 1
        if not (acceptance_array):
            pos_MCS[m+1] = pos_particles
            energy_arr[m+1] = energy

        if acceptance_array:
            acceptance_arr[m] = accepted / (n_particles*(m + 1))
    if acceptance_array:
        return acceptance_arr
    elif last_acceptance:
        return accepted / (n_particles*MCS)
    else:
        return pos_MCS, energy_arr, (accepted / (n_particles*(m + 1)))


def save_data(dLmax=dLmax, n_particles=n_particles, MCS=MCS, T=T, densidade=densidade):
    beta = 1 / (k*T)
    L = np.sqrt(n_particles / densidade)  # unidade de sigma
    print(L)
    pos, energy, acceptance = main_loop(dLmax=dLmax, beta=beta, n_particles=n_particles, 
                                        MCS=MCS, L=L)
    
    densidade_round = round(densidade, 3)
    # save positions:
    pos_reshaped = pos.reshape(pos.shape[0], -1)
    np.savetxt(f"positions_T{T}_N{n_particles}_d{densidade_round}_MCS{MCS}_dL_{dLmax}.txt", 
               pos_reshaped)

    # save energy:
    np.savetxt(f"energy_T{T}_N{n_particles}_d{densidade_round}_MCS{MCS}_dL_{dLmax}.txt", 
               energy)
    return pos, energy, acceptance


def open_pos(file, n_particles):
    loaded_pos = np.loadtxt(file)
    load_original_pos = loaded_pos.reshape(loaded_pos.shape[0], loaded_pos.shape[1] // n_particles, n_particles)
    return load_original_pos


"""### Rodar e salvar dados:

#### Rodar uma vez:
"""

dLmax = round(0.5*raio, 3)
pos, energy, acceptance = save_data(dLmax=dLmax)
print(f'dLmax={dLmax} \n beta={beta} \n n_particles={n_particles} \n MCS={MCS} \n\n pos[0]: \n {pos[0]}')
print(acceptance)

"""#### Rodar para vários T e rô:"""

dLmax = round(0.5*raio, 3)
n_particles = 32 
T_arr = np.array([0.1, 1.5, 3])
dens_arr = np.array([0.1, 0.5, 0.9])
for T in T_arr:
    print()
    print(f'T = {T}')
    for densidade in dens_arr:
        print(f'd = {densidade}')
        pos, energy, acceptance = save_data(dLmax=dLmax, n_particles=n_particles, MCS=MCS, T=T, densidade=densidade)
        #print(f'dLmax={dLmax} \n beta={beta} \n n_particles={n_particles} \n MCS={MCS} \n\n pos[0]: \n {pos[0]}')
        print(f'acceptance = {acceptance}')


"""
## Testes:

### Encontrar deslocamento máximo:
Testando valores:
"""

def testing_dL(possible_dL, times):
    for l in possible_dL:
        accept = np.zeros(times)
        for d in range(times):
            accept[d] = main_loop(dLmax=l*L, last_acceptance=True, acceptance_array=False)
        print(f'dLmax = {l}*L, acceptance = {np.mean(accept)}')

# Roda mais geral:
possible_dL = np.round(0.1*np.arange(1, 10), 1)
testing_dL(possible_dL, 5)

# Ajuste fino:
possible_dL = np.round(0.01*np.arange(10, 14), 3)
testing_dL(possible_dL, 50)

# Novo dLmax:
dLmax = 0.12*L
print(dLmax)

"""### Comportamento da acceptance:"""

def acceptance_behaviour(possible_dL, times):
    for d in range(times):
        fig, axes = plt.subplots(1, len(possible_dL), figsize=(20, 5))
        fig.suptitle(f'T = {T}   N = {n_particles}   d = {densidade_round}    dLmax = {round(dLmax, 2)}', fontsize=14)
        for l in range(len(possible_dL)):
            print(f'{l+1}/{len(possible_dL)}, {d+1}/{times}')
            acceptance = main_loop(dLmax=possible_dL[l]*raio, acceptance_array=True)
            axes[l].plot(np.arange(len(acceptance)), acceptance)
            axes[l].set_ylim([0, 1])
            axes[l].set_title(f'dLmax = {possible_dL[l]}*2^(-5/6)')
        plt.show()
        plt.close()

# Plotando acceptance
possible_dL = np.round(0.2*np.arange(1, 5), 1)
acceptance_behaviour(possible_dL, 1)

# Mais fino:
possible_dL = np.round(np.concatenate([0.0001*np.arange(1, 6)]), 4)
acceptance_behaviour(possible_dL, 1)


"""
## Figuras

### Intial and final positions:
"""

def scatter_pos(pos, indices, T, L, circles=True):
    graphs = len(indices)
    fig, axes = plt.subplots(1,graphs)
    fig.suptitle(f'T = {T}   N = {n_particles}   d = {densidade_round}    dLmax = {round(dLmax, 2)}', fontsize=14)

    for j in range(graphs):
        k = indices[j]
        if circles:
            # draw the circles where they are
            for i in range(n_particles):
                c = plt.Circle([pos[k][0][i], pos[k][1][i]], raio, fill=False, edgecolor='black', alpha = 0.5)
                axes[j].add_patch(c)
            # draw the circle's projections:
            for a in range(-1, 2):
                for b in range(-1, 2):
                    for i in range(n_particles):
                        c = plt.Circle([pos[k][0][i] + a*L, pos[k][1][i] + b*L], raio, fill=False, edgecolor='black', alpha=0.25)
                        axes[j].add_patch(c)
        
        points = axes[j].scatter(pos[k][0], pos[k][1])
        margem = raio
        axes[j].plot([0, L, L, 0, 0], [0, 0, L, L, 0], color='black')
        axes[j].axis([-margem, L + margem, -margem, L + margem], 'equal')
        axes[j].grid(visible=False)
        axes[j].set_aspect("equal")
        axes[j].set_title(f'passo {k}')
    return fig, axes, points


for T in T_arr:
    print()
    print(f'T = {T}')
    for densidade in dens_arr:
        print(f'd = {densidade}')
        densidade_round = round(densidade, 3)
        file_end = f"_T{T}_N{n_particles}_d{densidade_round}_MCS{MCS}_dL_{dLmax}"
        file_name = f"positions{file_end}.txt"
        pos = open_pos(file_name, n_particles=32)

        L = np.sqrt(n_particles / densidade)  # unidade de sigma
        plot = scatter_pos(pos=pos, indices=[0, pos.shape[0] - 1], T=T, L=L, circles=True)
        plt.show()
        plt.savefig(f"first_last_positions{file_end}.png")
        plt.close()

"""### Energy:"""

def y_limits(energy):
    energy_hist_range = energy[int(round(0.1*len(energy), 0)):]
    return [min(energy_hist_range)-1 , max([0, max(energy_hist_range) + 1])]

"""#### Energy graph:"""

for T in T_arr:
    print()
    print(f'T = {T}')
    for densidade in dens_arr:
        print(f'd = {densidade}')
        file_end = f"_T{T}_N{n_particles}_d{densidade_round}_MCS{MCS}_dL_{dLmax}"
        energy = np.loadtxt(f"energy{file_end}.txt")

        # Plot:
        fig, ax = plt.subplots(1, 1)
        titulo = f'T = {T}   N = {n_particles}   d = {densidade_round}    L = {round(L, 2)} \n dLmax = {round(dLmax, 2)}    acceptance = {round(acceptance, 2)}'
        fig.suptitle(titulo,
                    fontsize=14)
        energy_range = energy
        ax.plot(np.arange(len(energy_range)), energy_range)
        limites = y_limits(energy)
        print(limites)
        ax.set_ylim(limites)
        plt.show()
        plt.savefig(f"energy_graph{file_end}.png")
        plt.close()


        # Histogram:
        fig, ax = plt.subplots(1, 1)
        fig.suptitle(titulo,
                    fontsize=14)
        ax.hist(energy[100: ], density=True)
        ax.set_xlabel('energy')
        plt.show()
        plt.savefig(f"energy_histogram{file_end}.png")
        plt.close()

"""#### Energy histogram:"""



"""## Animação"""

file_name = f"positions_T{T}_N{n_particles}_d{densidade_round}_MCS{MCS}_dL_{dLmax}.txt"
print(file_name)

start = 0
end = len(pos)
pos = open_pos(file_name)[start:end]
fig, ax = plt.subplots(1,1, figsize=(5, 6))
fig.suptitle(f'T = {T}   N = {n_particles}   d = {densidade_round}    L = {round(L, 2)} \n dLmax = {round(dLmax, 2)}    acceptance = {acceptance}',
             fontsize=14)
margem = raio
ax.axis([-margem, L + margem, -margem, L + margem], 'equal')
ax.grid()
ax.set_aspect("equal")
ax.set_title(f'passo {k}')

c = []
for i in range(n_particles):
    c.append(plt.Circle([pos[0][0][i], pos[0][1][i]], raio, fill=False, color='lightgrey'))
    ax.add_patch(c[i])
scatter_points = ax.scatter(pos[0][0], pos[0][1], s=1000)


def animate(i):
    for k in range(n_particles):
        c[k].center = (pos[i][0][k], pos[i][1][k])
    scatter_points.set_offsets(pos[i].T)
    return scatter_points


anim = FuncAnimation(fig, animate, interval = 10, frames = end-start-1)

anim_file = f'animacao_T{T}_N{n_particles}_d{densidade_round}_MCS{MCS}_dL_{dLmax}.mp4'
print(anim_file)
anim.save(anim_file, writer = 'ffmpeg', fps = 20)

"""## Imagens:

### Raio:
"""

x0 = 1
y0 = 1
l = 2 * (2 ** 1/6)
triX = [x0, x0+l, x0+(l/2)]
h = np.sqrt(3)*l/2
triY = [y0, y0, y0 + h]

triX.append(triX[0])
triY.append(triY[0])

fig, ax = plt.subplots()

for i in range(3):
    c = plt.Circle([triX[i], triY[i]], l, alpha=0.5)
    c = plt.Circle([triX[i], triY[i]], l, alpha=0.5)
    c = plt.Circle([triX[i], triY[i]], l, alpha=0.5)
    ax.add_patch(c)

ax.plot(triX, triY, color = 'b')
ax.axis([x0-(l/2), x0 + (3*l/2), y0 - (l/2), y0 + h + l/2], 'equal')
ax.grid()
ax.set_aspect("equal")
plt.show()
plt.close()

"""### Potencial Lennard Jones:"""

def lennard_jones1d(r):
    sr6 = 1/(r ** 6)
    return 4 * (((sr6) ** 2) - (sr6))


xx = np.linspace(0, 4, 100)
yy = lennard_jones1d(xx)
fig, ax = plt.subplots(1, 1, figsize=(10, 4))
ax.plot([-10, 10], [0, 0], color='black')
ax.plot(xx, yy)
ax.set_ylabel('U(r)')
ax.set_xlabel('r')
ax.set_ylim([-1.5, 5])
ax.set_xlim([0, 3])
plt.show()
fig.savefig('lennard_jones_potential.png')
plt.close()
  1. ↑ J E Lennard-Jones 1931 Proc. Phys. Soc. 43 461
Disponível em “http://fiscomp.if.ufrgs.br/index.php?title=Potencial_de_Lennard-Jones&oldid=9069”