Modelo de Potts - 2D

O Modelo

Modelo de Potts pode ser considerado uma generalização do Modelo de Ising. Enquanto no Ising, os spins podem assumir valores 1 ou -1, no Modelo de Potts, os spins podem assumir valores que dependem de uma variavél $Q$ da seguinte forma: $\theta _{n}={\frac {2\pi n}{Q}}$. A quantidade $\theta _{n}$ nos fornece as possíveis orientações para os spins. Os valores que $n$ pode assumir são $n=1,2,3,...,Q$. Dessa forma, um Modelo de Potts bidimensional com $Q=10$ possui uma rede bidimensional de spins com 10 orientações diferentes. Nas figuras abaixo podemos ver três possíveis orientações dos spins.

Possibilidades de spin para $Q=2$.

Possibilidades de spin para $Q=3$.

Possibilidades de spin para $Q=4$.

O Hamiltoniano de interação, na ausência de campo magnético, pode ser escrito como

$H_{p}=-J\sum _{(i,j)}\delta (s_{i},s_{j})$

onde $J$ é a constante de acoplamento que determina a intensidade da interação e $\delta (s_{i},s_{j})$ é a delta de Kronecker, definida como 1 se $s_{i}=s_{j}$ e 0 se $s_{i}\neq s_{j}$.

Uma característica importante desse modelo é que as orientações em si não são relevantes, uma vez que o Hamiltoniano é definido por uma Delta de Kronecker. A única informação relevante é se os spins são iguais ou diferentes. Conforme veremos adiante, para o caso de $Q=2$, recaímos no conhecido Modelo de Ising.

Se incluirmos o campo magnético, o Hamiltoniado de Potts fica $H_{p}=-J\sum _{(i,j)}\delta (s_{i},s_{j})-\sum _{i}{\frac {1}{\beta }}h_{i}s_{i}$

onde $\beta =1/k_{B}T$ e $h_{i}$ é o campo magnético.

Relação com o Modelo de Ising

O Modelo de Ising é obtido quando tomamos $Q=2$ na expressão para $\theta _{n}$. Para que possamos reescrever o Hamiltoniano de Potts em uma forma semelhante ao Hamiltoniano de Ising, vamos somar uma constante aditiva, de modo que o Hamiltoniano fica

$H_{I}=H_{p}+\sum _{(i,j)}{\frac {J}{2}}=-J\sum _{(i,j)}\delta (s_{i},s_{j})+\sum _{(i,j)}{\frac {J}{2}}=-{\frac {J}{2}}\sum _{(i,j)}[2\delta (s_{i},s_{j})-1]$

Vemos que se os spins são iguais, obtemos $-J/2$ e se os spins são diferentes, obtemos $J/2$. No Modelo de Ising, nós tínhamos $-J$ e $J$, respectivamente. Uma consequência desse fator meio de diferença é que a temperatura crítica para o Modelo de Potts, para $Q=2$, é metade da temperatura crítica do Ising ($T_{c}\approx 1.1$) e os $\Delta Es$ nos histogramas de energia também são metade.

Algoritmo de Metropolis

Vamos implementar o Modelo de Potts utilizando o algoritmo de Metropolis.

O algoritmo de Metropolis é um método de Cadeia de Markov Monte Carlo (MCMC) para obter amostras aleatórias a partir de uma distribuição de probabilidade da qual a amostragem direta é difícil. O procedimento para a implementação do algoritmo é apresentado abaixo.

1) Escolhemos um estado inicial $x_{0}$, que em nosso caso será um spin orientado em uma direção dada por $Q$.

2) Através de um sorteio aleatório, com $Prob={\frac {1}{N}}$, escolhemos um candidato $x'$.

3) Calculamos a prababilidade de aceitação desse candidato atráves de $A(x',x_{t})=min\left(1,{\frac {P(x')}{P(x_{t})}}\right)$, onde $P(x')=\exp {-\beta E_{x}'}$

4) E então aceitamos ou rejeitamo este novo candidato da seguinte forma:

a) Gere um número aleatório uniforme $u\in [0,1]$;

b) E se $u\leq A(x',x_{t})$, aceite o novo estado e defina $x_{t+1}=x'$;

c) E se $u>A(x',x_{t})$, rejeite o novo estado e copie o estado antigo para frente $x_{t+1}=x_{t}$;

d) Incremente: coloque t = t + 1

Em nosso caso, a distribuição ${\frac {A(x,x')}{A(x',x)}}$ será $e^{-\beta \Delta E}$, onde $\Delta E=E_{x'}-E_{x}$.

Resultados das simulações

Definimos um Monte Carlo Step (MCS) como sendo o tempo em que a rede bidimensional com $L^{2}$ spins é percorrida pelo algoritmo. Ao final de $L^{2}$ flips de spin (seja com probabilidade $1$ ou com probabilidade $\exp(-\beta \Delta E)$), contamos um MCS. Além disso, em todas as simulações, utilizamos $T=1$ em unidades de $k_{B}$.

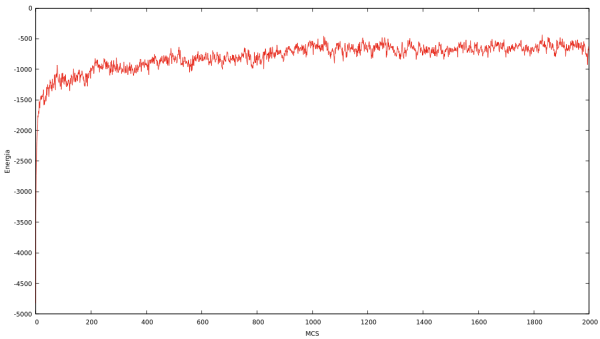
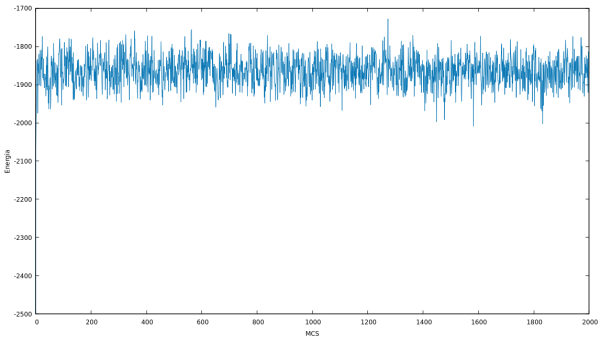
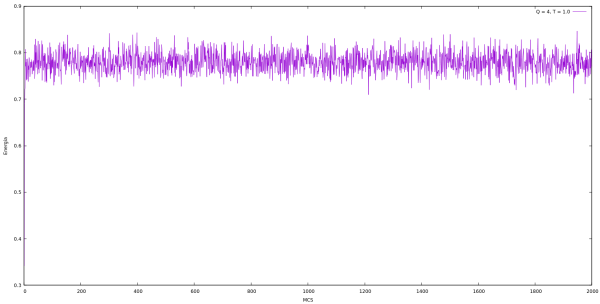
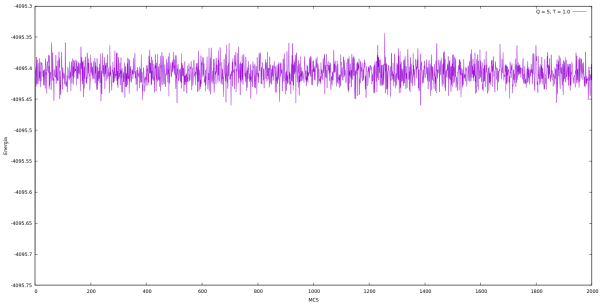
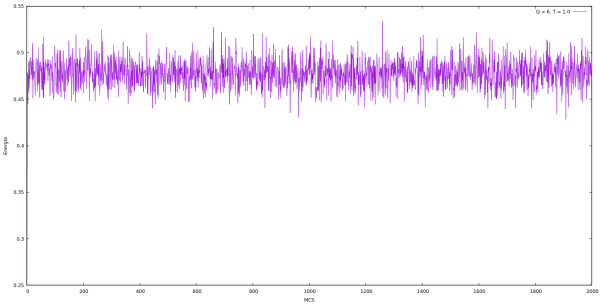
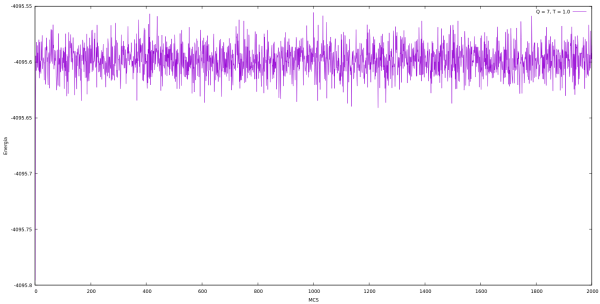
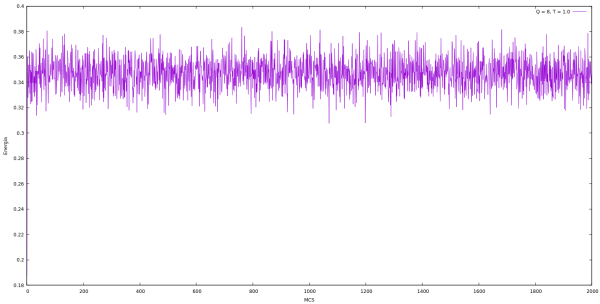
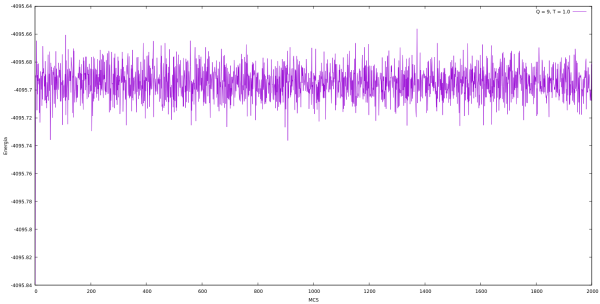
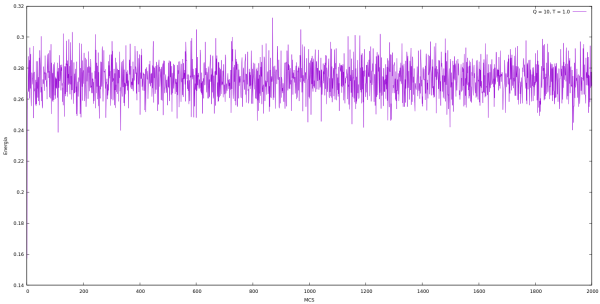
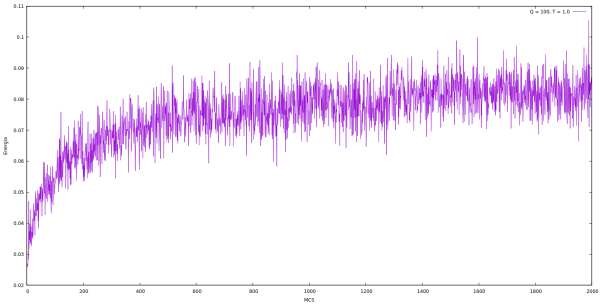
Energia

Energia em cada MCS para Q indo de 2 até 10 e L = 64 utilizando o algoritmo de Metropolis.
Energia média por MCS para Q = 2 e L = 64.	Energia média por MCS para Q = 3 e L = 64.
Energia média por MCS para Q = 4 e L = 64.	Energia média por MCS para Q = 5 e L = 64.
Energia média por MCS para Q = 6 e L = 64.	Energia média por MCS para Q = 7 e L = 64.
Energia média por MCS para Q = 8 e L = 64.	Energia média por MCS para Q = 9 e L = 64.
Energia média por MCS para Q = 10 e L = 64.	Energia média por MCS para Q = 100 e L = 64.

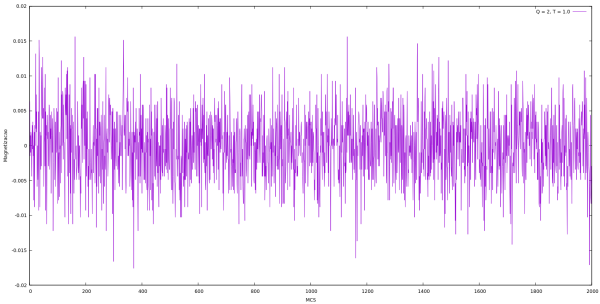
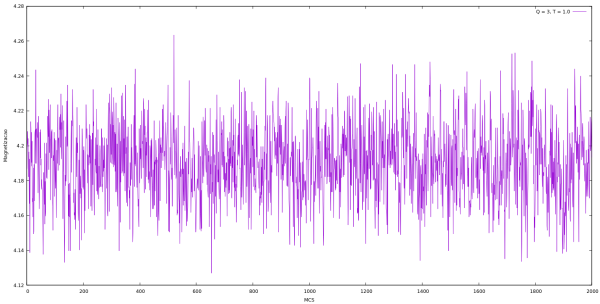
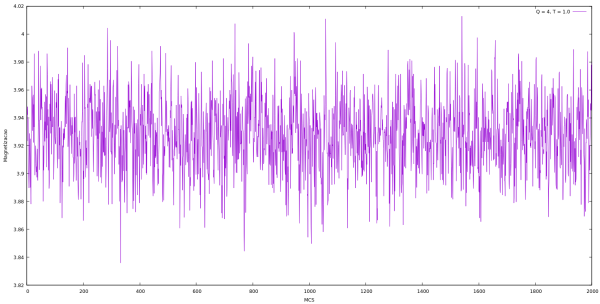
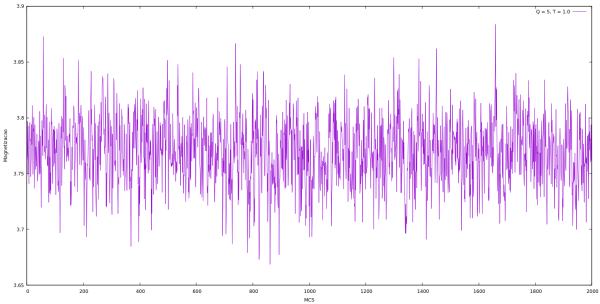
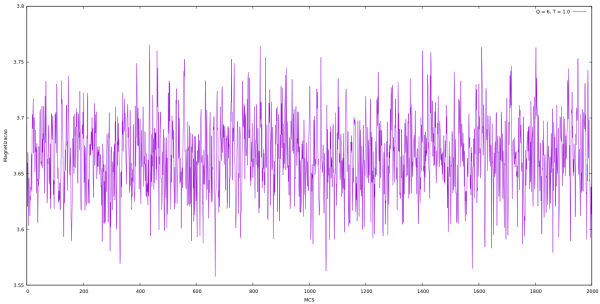
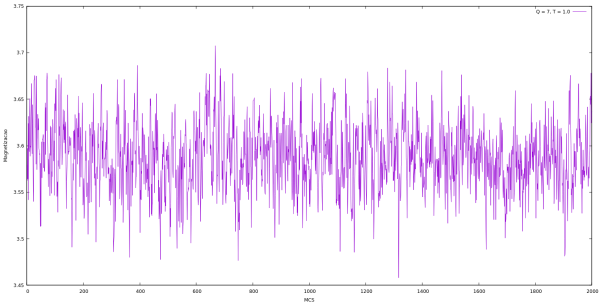
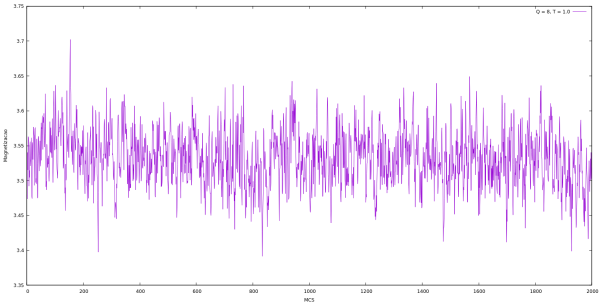
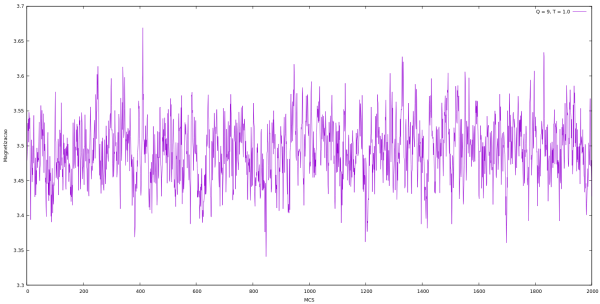
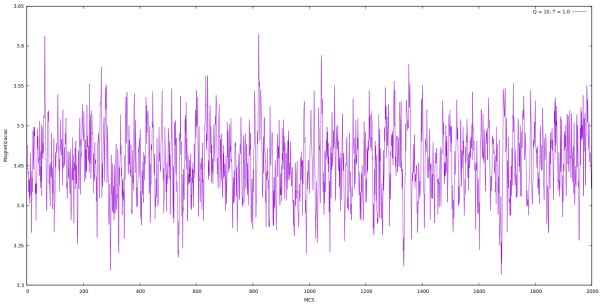
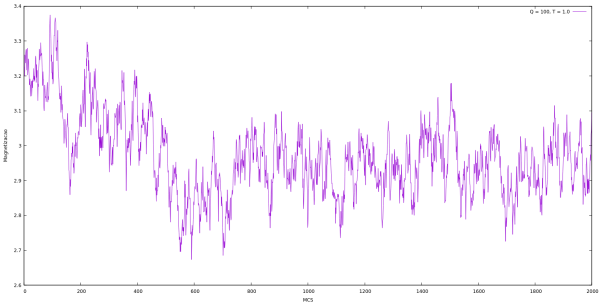
Magnetização

Magnetização em cada MCS para Q indo de 2 até 10 e L = 64 utilizando algoritmo de Metropolis.
Magnetização média por MCS para Q = 2 e L = 64.	Magnetização média por MCS para Q = 3 e L = 64.
Magnetização média por MCS para Q = 4 e L = 64.	Magnetização média por MCS para Q = 5 e L = 64.
Magnetização média por MCS para Q = 6 e L = 64.	Magnetização média por MCS para Q = 7 e L = 64.
Magnetização média por MCS para Q = 8 e L = 64.	Magnetização média por MCS para Q = 9 e L = 64.
Magnetização média por MCS para Q = 10 e L = 64.	Magnetização média por MCS para Q = 100 e L = 64.

Códigos utilizados

O código foi escrito em Fortran.

Metropolis - Potts 2D

Referências

D. P. Landau, K. Binder. A Guide Monte Carlo Simulations in Statistical Physics. Cambridge University. New York. 2000.

L. M. Barone, E. Marinari, G. Organtini, F. Ricci-Tersengui. Scientific Programming: C-Language, Algorithms and Models in Science. World Scientific. Singapore. 2013.