Equação de Swift-Hohenberg 2D

Trabalho desenvolvido no semestre de 2022/1 pelo aluno Artur Uhlik Fröhlich para a disciplina de Métodos Computacionais da Física C, ministrada pelo Professor Heitor Carpes Marques Fernandes.

Introdução

O problema escolhido foi a integração numérica da equação de Swift-Hohenberg em duas dimensões.

Boa parte dos aspectos teóricos desse trabalho tem como base o livro Pattern Formation and Dynamics in Nonequilibrium Systems, Cross & Greenside .

Essa equação pode aparecer nos estudos sobre convexão, equações diferenciais não lineares, formação de padrões e sistemas de não-equilíbrio. Ela possui diferentes versões mas a escolhida para esse trabalho foi a seguinte:

$\partial _{t}u=(r-1)u-2\nabla ^{2}u-\nabla ^{4}u-u^{3}$

na qual a dinâmica depende somente do parâmetro r.

O contexto de derivação dessa equação foi a convexão de Rayleigh-Bénard. Essa formulação possui virtudes mais analíticas do que práticas e apresenta vários aspectos comuns a modelos de formação de padrões e não é considerado uma descrição precisa de nenhum sistema experimental em específico.

Modificações dessa equação na sua parte não linear e nos coeficientes dos operadores diferenciais geram uma família extensa de EDPs não lineares que então podem servir de base para modelos de sistemas físicos reais.

Integração em 1D

O objetivo final é chegar na Equação de Swift-Hohenberg em duas dimensões mas antes é pertinente verificar a integração em uma dimensão.

Para realizar a integração foram utilizadas as FFTs (Transformadas Rápidas de Fourier) e o método foi baseado nos vídeos e livro do Professor Steven Bruton .

O princípio do método é utilizar as transformadas para calcular as derivadas no espaço transformado (que são bem mais simples) e retornar com esses valores para o espaço cartesiano e então com as derivadas calculadas é realizada a evolução temporal utilizando o método de Euler explícito (no caso desse trabalho a integração em 1-D utilizou o integrador da biblioteca Scipy).

Então antes de adentrar no código é preciso fazer a transformada da equação em 1-D, dado que:

${\mathcal {F}}\{u(x,t)\}={\hat {u}}(k,t)$,

${\mathcal {F}}\left\{{\frac {d^{n}u}{dx^{n}}}\right\}=(ik)^{n}{\hat {u}}$.

Então a equação fica:

${\mathcal {F}}\left\{{\frac {du}{dt}}\right\}=(r-1){\hat {u}}+2k^{2}{\hat {u}}-k^{4}{\hat {u}}-{\hat {(u^{3})}}$.

Dessa maneira transformamos uma equação diferencial parcial em uma equação diferencial ordinária, pois só possui a derivada temporal. Nesse caso de integração numérica ficamos com um sistema de várias equações diferenciais ordinárias para cada $k$.

Com isso é possível escrever um código capaz de fazer a transformada do estado, calcular as derivadas no espaço de Fourier e voltar para o espaço cartesiano e realizar a evolução temporal, tudo isso dentro de um passo da integração.

O código é análogo ao que será apresentado posteriormente em duas dimensões então somente os resultados serão mostrados aqui (todos os códigos se encontram no link para o GitHub )

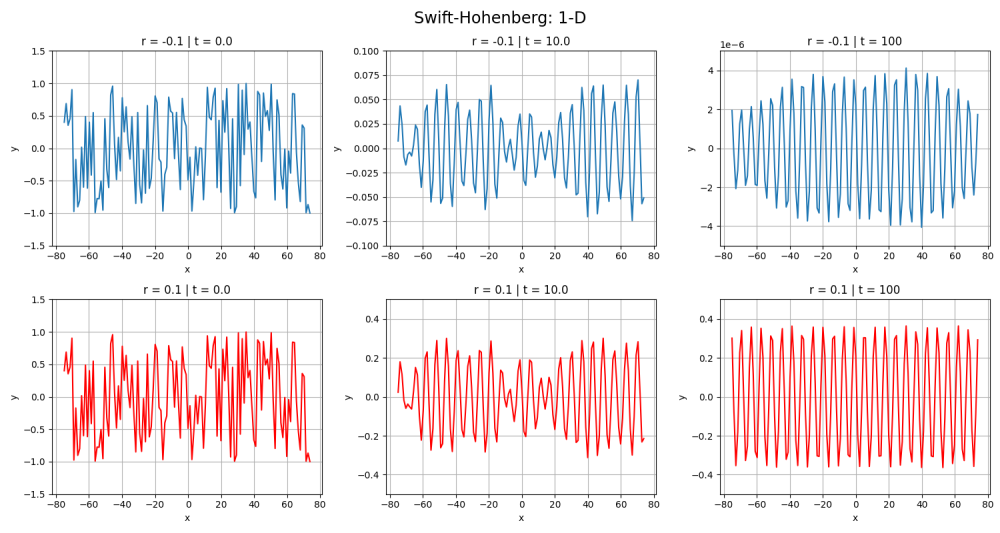
Para testar o comportamento da equação perante diferentes valores do parâmetro $r$, teste esse inspirado pela análise de instabilidade linear feita no capítulo 2 do livro do Cross & Greenside, na qual é encontrado que o valor crítico de $r$ é 0, e que para $r$><0 o estado apresenta uma evolução diferente em comparação com $r$>0, exemplos disso são as integrações a seguir:

Diferentes integrações da Equação de Swift-Hohenberg em uma dimensão usando r=-0.1 (azul) e r=0.1 (vermelho)

Pode-se notar que para $r$<0 a solução homogênea se torna estável, estabiliza no 0, e para $r$>0 o estado é instável e se mantém em constante movimento mas com as "ondas" de magnitude constante.

Com esses resultados podemos ir para a integração em duas dimensões.

Integração em 2D

Para começar a explicar o código devemos discretizar o espaço de Fourier com os seus respectivos números de onda kappa para cada dimensão (já que o campo escalar tem duas dimensões a transformada retorna um campo também de duas dimensões só que no espaço de Fourier).

Os parâmetros N e L determinam o tamanho do campo escalar e a sua definição, testes realizados com esse código retornam um limite inferior de aproximadamente de 0.39 no parâmetro dx.

# Todos os parâmetros estão aqui:
N = 256
L = 100
dx = L/N
r = 0.25
dt = 0.0001
tf = 100
checkpoint = 500
# *-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
x = np.arange(-L/2, L/2, dx)
y = np.arange(-L/2, L/2, dx)
size = len(x)

# Os coeficientes
kx = 2 * np.pi * np.fft.fftfreq(N, d=dx)
ky = 2 * np.pi * np.fft.fftfreq(N, d=dx)
kappax, kappay = np.meshgrid(kx, ky)

Em seguida está a função que utiliza a FFT para calcular o lado direito da equação de Swift-Hohenberg apresentada na introdução. Com os métodos da biblioteca Scipy o campo escalar inicial será transformado e com ele serão aplicadas as propriedades das transformadas de Fourier para as derivadas da seguinte maneira.

Dado que:

${\mathcal {F}}\{u(x,y,t)\}={\hat {u}}(k_{x},k_{y},t)$

${\mathcal {F}}\{\partial ^{n}u\}=(ik)^{n}{\hat {u}}$

O lado direito da equação transformado então fica assim:

${\mathcal {F}}\{\partial _{t}u\}=(r-1){\hat {u}}+2k_{x}^{2}{\hat {u}}+2k_{y}^{2}{\hat {u}}-k_{x}^{4}{\hat {u}}-k_{y}^{4}{\hat {u}}-2k_{x}^{2}k_{y}^{2}{\hat {u}}-{\hat {(u^{3})}}$

Todo esses termos ao lado direito foram chamados de RHS (Right Hand Side) e calculados na função seguinte.

def rhs(u, kappax, kappay, r):
    '''
    Calcula o lado direito da EDP
    '''
    kpx2 = np.power(kappax, 2)
    kpx4 = np.power(kappax, 4)
    kpy2 = np.power(kappay, 2)
    kpy4 = np.power(kappay, 4)
    uhat = fft2(u)
    uhat3 = fft2(u**3)
    duhatx2 = kpx2 * uhat
    duhaty2 = kpy2 * uhat
    duhatx4 = kpx4 * uhat
    duhaty4 = kpy4 * uhat
    duhatxy = kpx2 * kpy2 * uhat
    duhat = (r - 1)*uhat + 2*duhatx2 + 2*duhaty2 - duhatx4 - duhaty4 - 2*duhatxy - uhat3
    dut = ifft2(duhat)
    return dut.real

Como essa função retorna nosso vetor de estado no espaço cartesiano isso possibilita a realização da evolução temporal da equação utilizando o método de Euler explícito, a partir da criação de um estado inicial (um campo escalar que nesse caso foi inicializado utilizando uma distribuição uniforme de números aleatórios, todas as imagens geradas nesse trabalho usaram 666 como semente dos números aleatórios).

# Matriz do estado inicial
u0 = np.random.uniform(-1, 1, (size, size))

# Array da evolução temporal
track = [copy.deepcopy(u0)]

# A integração ocorre aqui
c = 0
t = np.arange(0, tf, dt)
for ti in t:
    c += 1
    u0 += dt * rhs(u0, kappax, kappay, r)
    if c % checkpoint == 0:
        track.append(copy.deepcopy(u0))
    if ti % 2 == 0:
        print(f't = {ti}')

Resultados

Foi realizada a integração com diferentes valores de $r$ para testar as características vistas em uma dimensão, abaixo está o resultado de uma integração usando um $r$<0:

Integração de Swift-Hohenberg em 2D utilizando r=-0.25

Parece uma imagem chata e sem graça mas o que ela nos mostra é que o estado evoluiu para uma solução estável em 0, assim como encontrado em 1 dimensão anteriormente.

Realizando a integração com um valor de $r$>0 obtemos o seguinte:

Integração de Swift-Hohenberg em 2D utilizando r=0.25 e dt=0.0001

Podemos ver que para um $r$>0 o estado não atinge o equilíbrio e evolui constantemente, exemplificando mais uma vez o resultado obtido em 1D.

Outra característica interessante de se notar em 2D se chama "coarsening" que pode ser traduzida como "engrossamento". Esse é o efeito que vemos na evolução do padrão no qual ele vai aumentando as áreas de domínio das suas faixas.

Podemos ver a evolução desses padrões no vídeo da integração gerado por um dos códigos presentes no GitHub.

Outro exemplo desse efeito (coarsenning) também pode ser visto na literatura:

Simulação da equação de Swift-Hohenberg em uma grande geometria periódica de tamanho 256 × 256 com r = 0.25, começando com condições iniciais aleatórias . O aumento do tamanho médio do domínio no painel (a) no tempo 10 para o painel (b) no tempo 10000 é o chamado “coarsening”.)