Grupo2 - Ondas1: mudanças entre as edições
| Linha 30: | Linha 30: | ||
Apresentaremos aqui três abordagens diferentes para a solução da equação diferencial parcial apresentada, e após, seus respectivos erros associados. A respeito das discretizações, <math> j </math> corresponde à posição, e <math> n </math> representa o tempo. | Apresentaremos aqui três abordagens diferentes para a solução da equação diferencial parcial apresentada, e após, seus respectivos erros associados. A respeito das discretizações, <math> j </math> corresponde à posição, e <math> n </math> representa o tempo. | ||
===Método de Lax-Friedrichs=== | ===Método de Lax-Friedrichs - <math> O(\Delta x^2, \Delta t )</math> === | ||
Esse método consiste em discretizar as equações no esquema FTCS, ou seja | Esse método consiste em discretizar as equações no esquema FTCS, ou seja | ||
Edição das 07h08min de 24 de outubro de 2017
Introdução
A modelagem numérica vem se tornando cada vez mais uma ferramenta indispensável para um engenheiro. Tal modelagem pode trazer informações importantes para entender como melhor abordar o desenvolvimento de um projeto, neste caso, um que envolva ondas. Nós, como futuros engenheiros físicos, pensamos em trazer um problema mais "concreto", de engenharia costeira e portuária, que pode ou não surgir em nossas vidas profissionais mas cujo método de solução certamente estará presente. Aqui será apresentado um modelo baseado em uma condição inicial e um perfil topográfico do local estudado que descreve a evolução temporal de uma onda.
Para testarmos os diferentes métodos, utilizaremos a equação da onda em uma dimensão, que é uma equação diferencial parcial de segunda ordem, para modelarmos uma corda:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^{2} u}{\partial x^{2}} }
em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(x, t) } é o deslocamento vertical da corda e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0<x<L } , com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L } o comprimento da corda.
Admitindo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle c=1} ,
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial t} \Big( \frac{\partial u}{\partial t} \Big) = \frac{\partial}{\partial x} \Big( \frac{\partial u}{\partial x} \Big) } .
Uma vez que os métodos citados abaixo são para equações de primeira ordem, é necessário separarmos a equação em um sistema de equações, fazendo a substituição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v=\frac{\partial u}{\partial t} } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w= \frac{\partial u}{\partial x} } :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ \begin{array}{cc} \frac{\partial v}{\partial t}=\frac{\partial w}{\partial x} \\ \\ \frac{\partial v}{\partial x}=\frac{\partial w}{\partial t} \\ \end{array}\right.}
As condições de contorno são Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(0, t) = u(L, t) = 0 } (pontas fixas), e as condições iniciais são Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(x,0) = \sin{\frac{\pi x}{L}} } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial u}{\partial t}(x, 0) = 0 }
Algoritmos
Apresentaremos aqui três abordagens diferentes para a solução da equação diferencial parcial apresentada, e após, seus respectivos erros associados. A respeito das discretizações, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j } corresponde à posição, e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n } representa o tempo.
Método de Lax-Friedrichs - Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle O(\Delta x^2, \Delta t )}
Esse método consiste em discretizar as equações no esquema FTCS, ou seja
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{j}^{n+1} = v_j^n + \frac{\Delta t}{2\Delta x}(w_{j+1}^{n} - w_{j-1}^{n}) } ,
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{j}^{n+1} = w_j^n + \frac{\Delta t}{2\Delta x}(v_{j+1}^{n} - v_{j-1}^{n}) }
,
Entretanto, ao se realizar uma análise de estabilidade de Von Neumann, conclui-se que esse método é instável. Para torná-lo estável, é necessário trocarmos os termos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_j^n } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_j^n } por suas médias espaciais
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{j}^{n+1} = \Big( \frac{ v_{j-1}^{n} + v_{j+1}^{n}}{2} \Big) + \frac{\Delta t}{2\Delta x}(w_{j+1}^{n} - w_{j-1}^{n}) }
,
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{j}^{n+1} = \Big( \frac{ w_{j-1}^{n} + w_{j+1}^{n}}{2} \Big) + \frac{\Delta t}{2\Delta x}(v_{j+1}^{n} - v_{j-1}^{n}) }
,
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{j}^{n+1} = u_{j}^{n} + v_{j}^{n}\Delta t } ,
Embora as médias espaciais sejam necessárias para a estabilidade do método, elas introduzem um problema: surge um efeito chamado de dissipação numérica, ou seja, a amplitude da solução diminui com o tempo. Isso pode ser observado através da análise de Von Neumann ou de uma investigação da equação do esquema Lax-Friedrichs. Por este método, observa-se que ao inserirmos as médias, mudamos a equação original do problema, pois agora há também um termo do tipo difusivo (uma derivada segunda).
Agora vamos unir todas as equações, para que no programa possamos iterar apenas uma equação ao invés de três.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{j}^{n+1} = u_{j}^{n} + \Big( \frac{u_{j-1}^{n} + u_{j+1}^{n}}{2} \Big) - \Big( \frac{u_{j-1}^{n-1} + u_{j+1}^{n-1}}{2} \Big) + \frac{(\Delta t)^2}{4(\Delta x)^2} \Big( u_{j-2}^{n-1} -2u_{j}^{n-1} + u_{j+2}^{n-1}\Big) }
.
Método de Leapfrog
Neste método utilizamos os pontos intermediários da discretização. Para v temos
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ v_{j}^{n+\frac{1}{2}} - v_{j}^{n-\frac{1}{2}}}{\Delta t} = \frac{ w_{j+\frac{1}{2}}^{n} - w_{j-\frac{1}{2}}^{n} }{\Delta x} \Rightarrow v_{j}^{n+\frac{1}{2}} = v_{j}^{n-\frac{1}{2}} + \frac{\Delta t}{\Delta x} (w_{j+\frac{1}{2}}^{n} - w_{j-\frac{1}{2}}^{n} ) } ,
Para w temos
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ v_{j+1}^{n+\frac{1}{2}} - v_{j}^{n+\frac{1}{2}}}{\Delta x} = \frac{ w_{j+\frac{1}{2}}^{n+1} - w_{j+\frac{1}{2}}^{n} }{\Delta t} \Rightarrow w_{j+\frac{1}{2}}^{n+1} = w_{j+\frac{1}{2}}^{n} + \frac{\Delta t}{\Delta x} \Big(v_{j+1}^{n+\frac{1}{2}} - v_{j}^{n+\frac{1}{2}}\Big) } ,
Para u temos
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{j}^{n+\frac{1}{2}} = \frac{\partial u}{\partial t} \Big|_{j}^{n+\frac{1}{2}} = \frac{ u_{j}^{n+1} - u_j^n}{\Delta t} \Rightarrow u_{j}^{n+1} = u_j^n + v_{j}^{n+\frac{1}{2}} \Delta t} ,
Juntando todas elas temos
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{j}^{n+1} = 2u_{j}^{n} - u_{j}^{n-1} + \frac{(\Delta t)^2}{(\Delta x)^2}(u_{j+1}^{n} - 2u_{j}^{n} + u_{j-1}^{n}) } ,
o que é equivalente a discretizarmos a equação da onda diretamente, utilizando que, para uma função f(x), Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2f}{dx^2}\Big|_j = \frac{f_{j-1} - 2f_j + f_{j+1}}{(\Delta x)^2}} ,
sendo j a discretização em x.
Método de Lax-Wendroff de Dois Passos
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{j+\frac{1}{2}}^{n+\frac{1}{2}} = \frac{1}{2}( v_{j+1}^{n} + v_{j}^{n} ) + \frac{\Delta t }{2\Delta x} (w_{j+1}^{n} - w_{j}^{n}) } ,
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{j-\frac{1}{2}}^{n+\frac{1}{2}} = \frac{1}{2}( v_{j}^{n} + v_{j-1}^{n} ) + \frac{\Delta t }{2\Delta x} (w_{j}^{n} - w_{j-1}^{n}) } ,
Para w resulta em:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{j}^{n+1} = w_j^n + \frac{\Delta t}{\Delta x} \Bigg[\frac{1}{2}(v_{j+1}^{n} - v_{j-1}^{n}) + \frac{\Delta t}{2\Delta x} (w_{j+1}^{n} - 2 w_{j}^{n} + w_{j-1}^{n})\Bigg] } ,
Agora encontraremos a equação para v:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{j}^{n+1} = v_{j}^{n} + \frac{\Delta t}{\Delta x} \Big(w_{j+\frac{1}{2}}^{n+\frac{1}{2}} - w_{j-\frac{1}{2}}^{n+\frac{1}{2}}\Big) } ,
Sendo que:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{j+\frac{1}{2}}^{n+\frac{1}{2}} = \frac{1}{2}( w_{j+1}^{n} + w_{j}^{n} ) + \frac{\Delta t }{2\Delta x} (v_{j+1}^{n} - v_{j}^{n}) } ,
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{j-\frac{1}{2}}^{n+\frac{1}{2}} = \frac{1}{2}( w_{j}^{n} + w_{j-1}^{n} ) + \frac{\Delta t }{2\Delta x} (v_{j}^{n} - v_{j-1}^{n}) } ,
Para v resulta em:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{j}^{n+1} = v_j^n + \frac{\Delta t}{\Delta x} \Bigg[\frac{1}{2}(w_{j+1}^{n} - w_{j-1}^{n}) + \frac{\Delta t}{2\Delta x} (v_{j+1}^{n} - 2 v_{j}^{n} + v_{j-1}^{n})\Bigg] } ,
E finalmente temos a equação unificada das outras em u:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{j}^{n+1} = 2u_{j}^{n} - u_{j}^{n-1} + \frac{(\Delta t)^2}{2(\Delta x)^2}\Bigg[ \Big(\frac{ u_{j+2}^{n-1} - u_{j}^{n-1}}{2} \Big) - \Big(\frac{u_{j}^{n-1} - u_{j-1}^{n-1}}{2} \Big) + u_{j+1}^{n} - u_{j+1}^{n-1} - 2u_{j}^{n} + 2u_{j}^{n-1} + u_{j-1}^{n} - u_{j-1}^{n-1}\Bigg] } ,
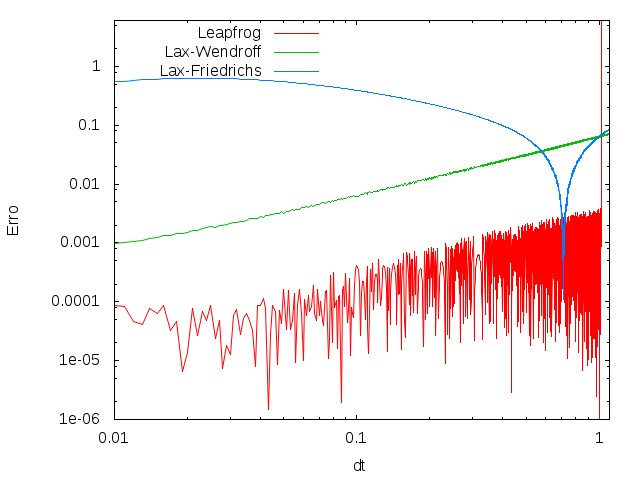
Análise de erros e estabilidade
A análise de erros se torna mais evidente durante a escolha do parâmetro Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k = \frac{dt}{dx}} . Valores grandes trazem pouca acurácia, e valores pequenos necessitam de muito poder de computação (tempo e dinheiro). Trazemos problemas mais simplificados como um "guia" de escolha do parâmetro.
A partir do cálulo da solução analítica da equação da onda, podemos calcular quanto o valor obtido pelos métodos difere da solução real, o que leva a uma visualização do erro corrente em cada método de integração.
Podemos observar a ordem com que os erros crescem à medida que o parâmetro k se torna maior. Lembrando que os valores da constante são determinados pela discretização do espaço e do tempo.
Simulação de Propagação de Onda 2D Dependente de Topografia
O modelo mais simples parte da equação da onda [1], acrescentando o termo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(x,y,t)} .
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^2 u}{\partial t^2} = \Big( \frac{\partial}{\partial x} H(x,y,t) \frac{\partial u}{\partial x}\Big) + \Big( \frac{\partial}{\partial y} H(x,y,t) \frac{\partial u}{\partial y}\Big) - \frac{\partial^2 H}{\partial t^2} } ,
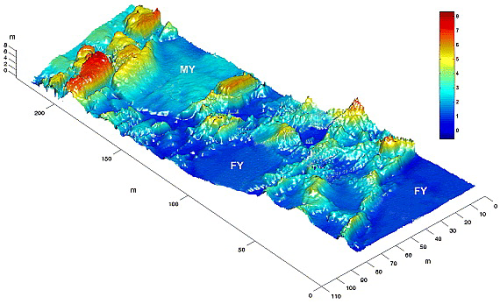
Sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(x,y,t)}
uma representação da profundidade em águas calmas. Em uma situação real, pode-se obtê-la por mapeamento eletrônico do terreno por sistema de sonar.
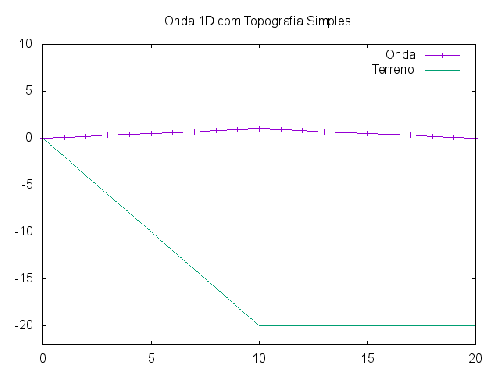
Como primeira abordagem visando uma análise em 2D, a integração da equação em 1D (mesmo sendo uma situação muito idealizada) já traz resultados interessantes. Podemos observar, por exemplo, que a amplitude da onda cresce perto da costa. Esta informação por si só ajuda na construção de proteção contra quebra de ondas, pois é obtido o tamanho que as mesmas atingem.
É importante notar o quão poderosa é a integração de equações parciais na vida de um engenheiro.
A dependência em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(x,y,t)} permite um modelo no qual o terreno se modifica com o tempo. Isto é, pode-se observar o efeito que o deslocamento de placas tectônicas, deslizamentos, e até explosões provocam no comportamento das ondas na costa de um país e o reconhecimento de áreas críticas.
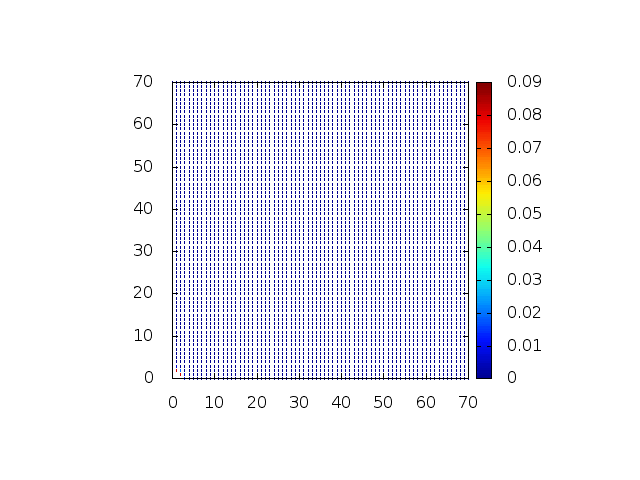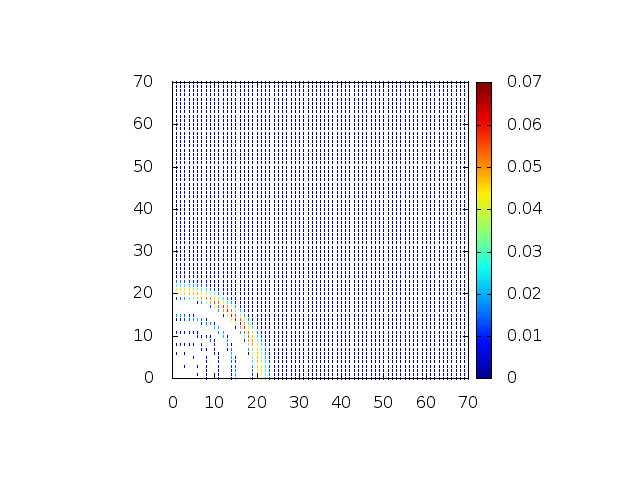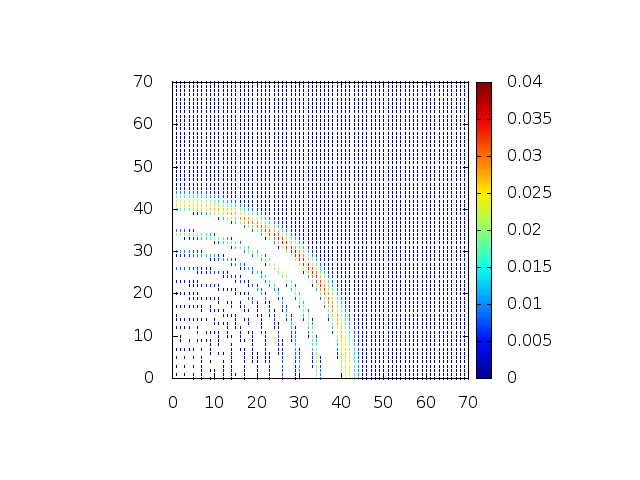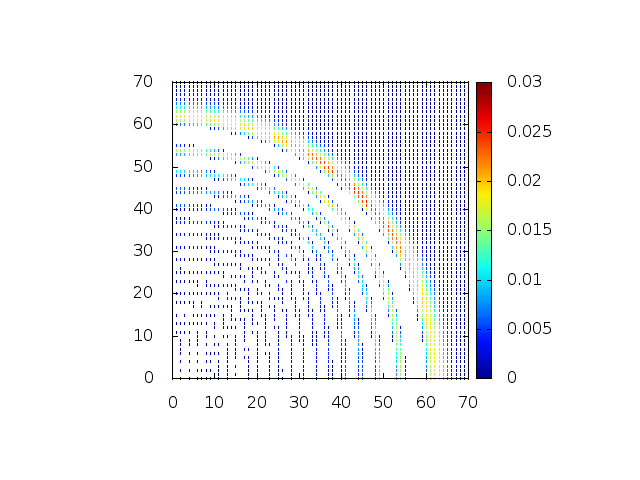
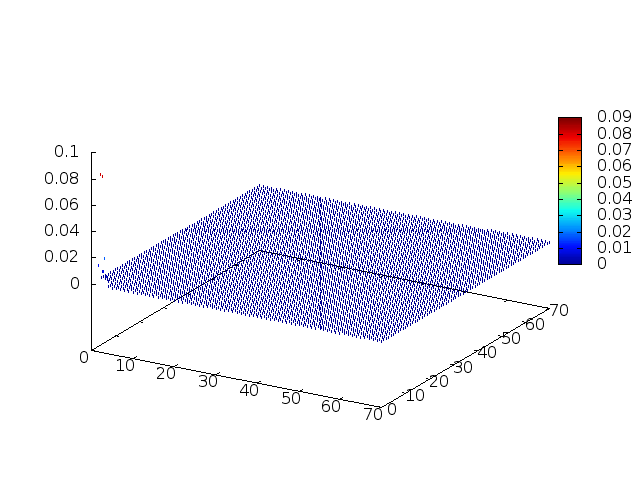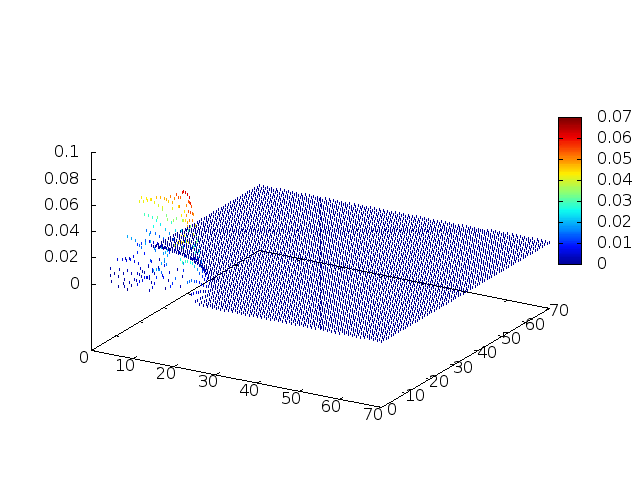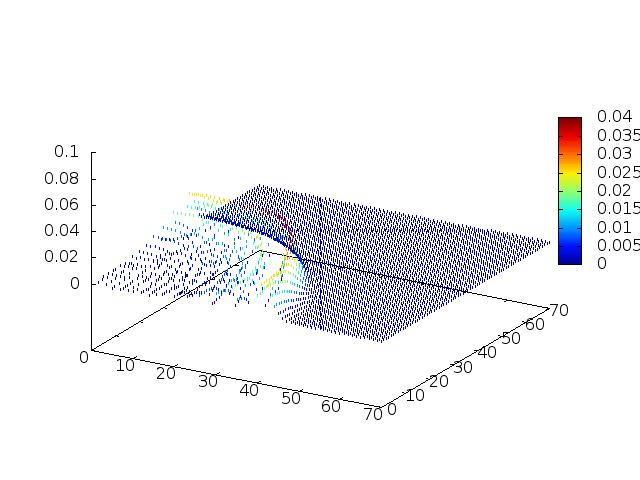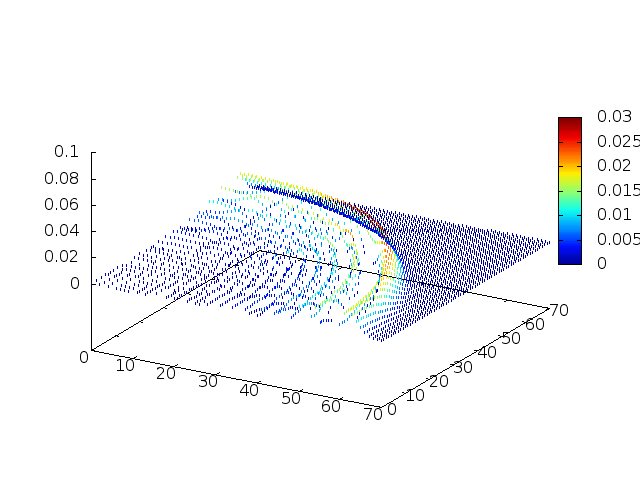
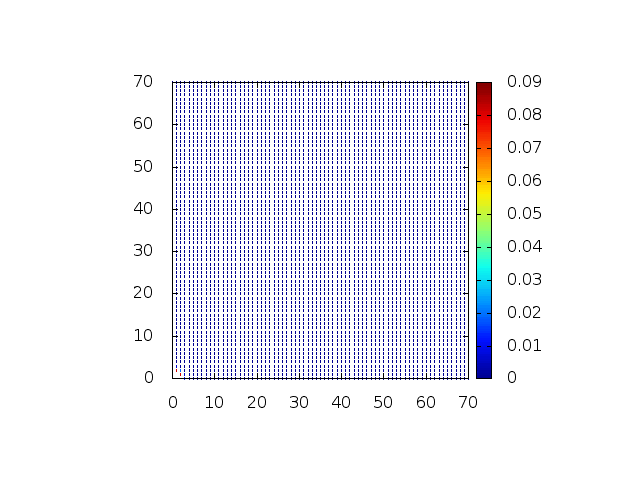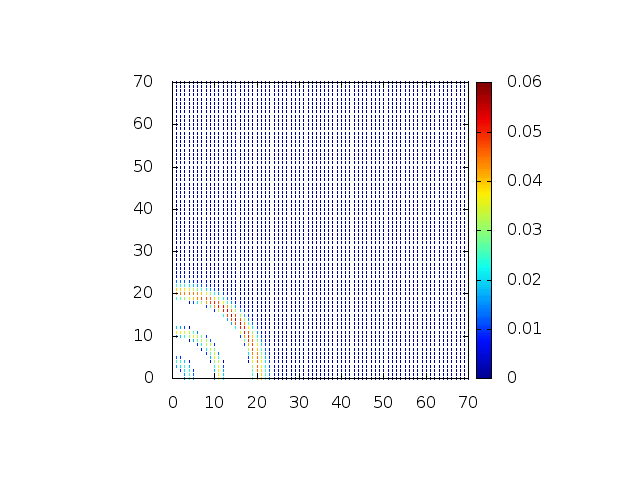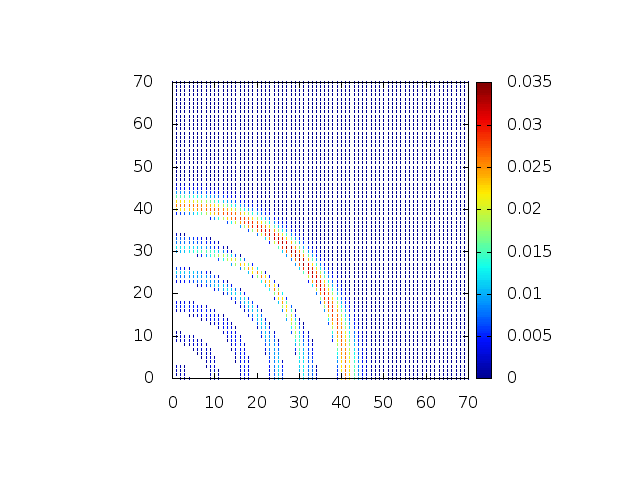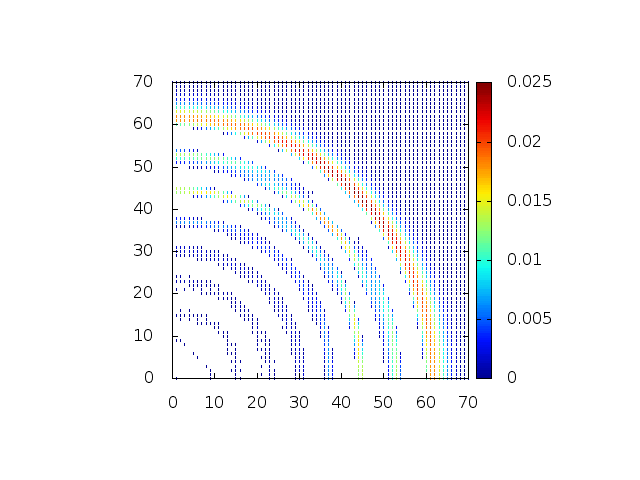
Estendendo o algoritmo do Leap-Frog à situação 2D, obtemos, para uma dada condição inicial e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(x,y,t) = C} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} é uma constante:
Podemos então, analisar como a mesma condição inicial se porta quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(x,y,t)}
descreve uma gaussiana na origem:
Bibliografia
1"The Wave Equation in 1D and 2D," por Knut–Andreas Lie, Dept. of Informatics, University of Oslo; disponível em: [1]; Último acesso em 23/10/2017.
2"Digital terrain mapping of the underside of sea ice from a small AUV," por Wadhams, M. J. Doble; disponível em: DOI: 10.1029/2007GL031921 ; Último acesso em 23/10/2017.
2 Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007). Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8.
2 "Métodos Computacionais da Física C - Aula 2 - 2016/1" por Heitor C. M. Fernandes, Instituto de Física, UFRGS; Último acesso em 23/10/2017.