Grupo2 - Ondas1: mudanças entre as edições
Sem resumo de edição |
|||
| Linha 93: | Linha 93: | ||
O modelo mais simples parte da equação da onda [1], acrescentando o termo <math>H(x,y,t)</math>. | O modelo mais simples parte da equação da onda [1], acrescentando o termo <math>H(x,y,t)</math>. | ||
<math> \frac{\partial^2 u}{\partial t^2} = \Big( \frac{\partial}{\partial x} H(x,y,t) \frac{\partial u}{\partial x}\Big) + \Big( \frac{\partial}{\partial y} H(x,y,t) \frac{\partial u}{\partial y}\Big) - \frac{\partial^2 H}{\partial t^2} </math> , | |||
Sendo <math>H(x,y,t)</math> uma representação da profundidade em águas calmas. Em uma situação real, pode-se obtê-la por mapeamento eletrônico do terreno por sistema de sonar. | Sendo <math>H(x,y,t)</math> uma representação da profundidade em águas calmas. Em uma situação real, pode-se obtê-la por mapeamento eletrônico do terreno por sistema de sonar. | ||
| Linha 100: | Linha 100: | ||
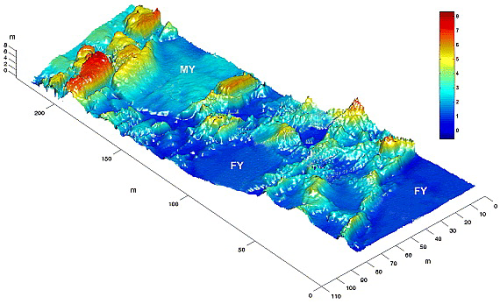
[[Arquivo:Grupo2_ondas1_imagem1.png |500px|center| Exemplo de mapeamento de terreno sub - calota polar feito por AUV (''autonomous underwater vehicle'')]] | [[Arquivo:Grupo2_ondas1_imagem1.png |500px|center| Exemplo de mapeamento de terreno sub - calota polar feito por AUV (''autonomous underwater vehicle'')]] | ||
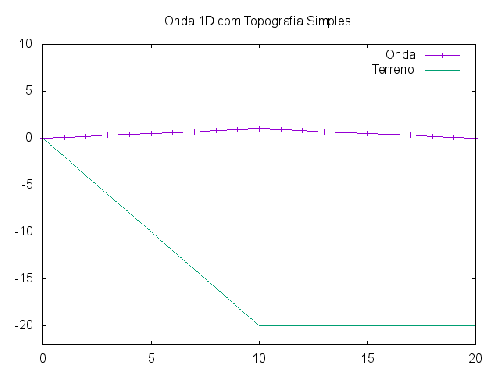
Como primeira abordagem , a integração da equação em 1D (mesmo sendo uma situação muito idealizada) já traz resultados interessantes. Podemos observar, por exemplo, que a amplitude da onda cresce perto da costa. Esta informação por si só ajuda na construção de proteção contra quebra de ondas, pois é obtido o tamanho que as mesmas atingem. | Como primeira abordagem visando uma análise em 2D, a integração da equação em 1D (mesmo sendo uma situação muito idealizada) já traz resultados interessantes. Podemos observar, por exemplo, que a amplitude da onda cresce perto da costa. Esta informação por si só ajuda na construção de proteção contra quebra de ondas, pois é obtido o tamanho que as mesmas atingem. | ||
[[Arquivo:Grupo2_ondas1_imagem2.gif |500px|center| Simulação em 1D de ondas perto da margem ]] | [[Arquivo:Grupo2_ondas1_imagem2.gif |500px|center| Simulação em 1D de ondas perto da margem ]] | ||
| Linha 106: | Linha 106: | ||
É importante notar o quão poderosa é a integração de equações parciais na vida de um engenheiro. | É importante notar o quão poderosa é a integração de equações parciais na vida de um engenheiro. | ||
A | A dependência em <math>t</math> de <math>H(x,y,t)</math> permite um modelo no qual o terreno se modifica com o tempo. Isto é, pode-se observar o efeito que o deslocamento de placas tectônicas, deslizamentos, e até explosões provocam no comportamento das ondas na costa de um país e o reconhecimento de áreas críticas. | ||
Estendendo o algoritmo do Leap-Frog à situação 2D, obtemos, para uma dada condição inicial e <math>H(x,y,t) = C</math>, onde C é uma constante: | |||
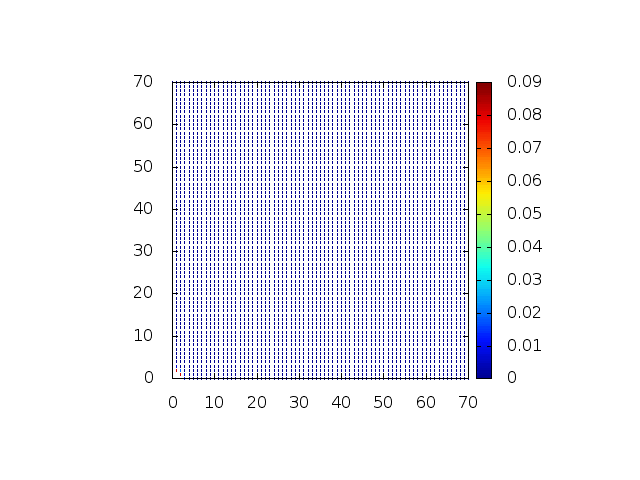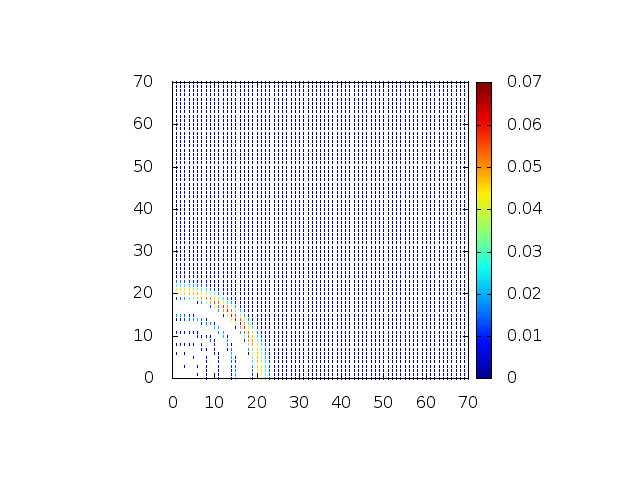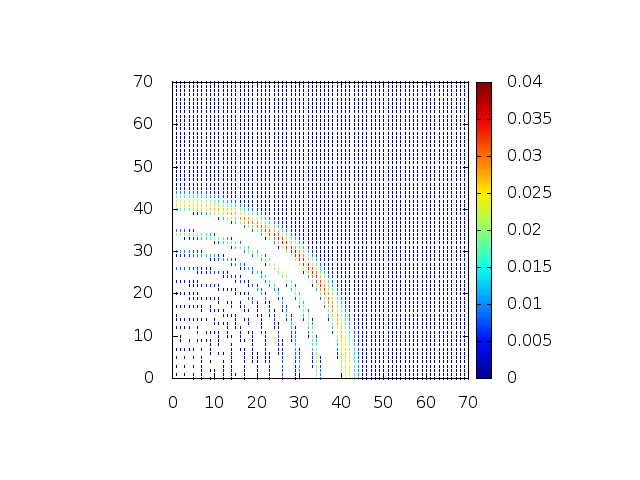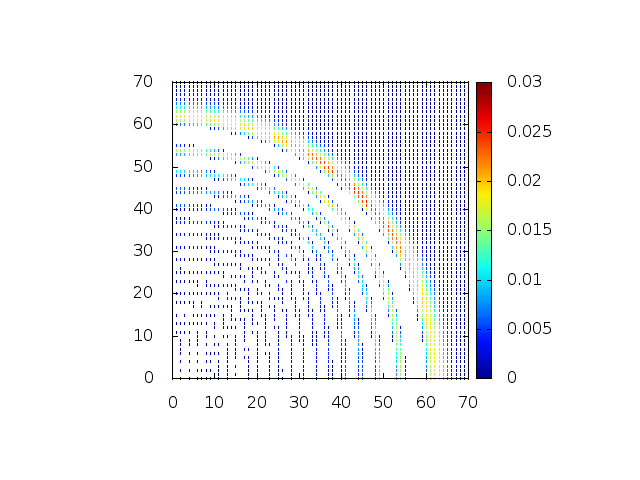
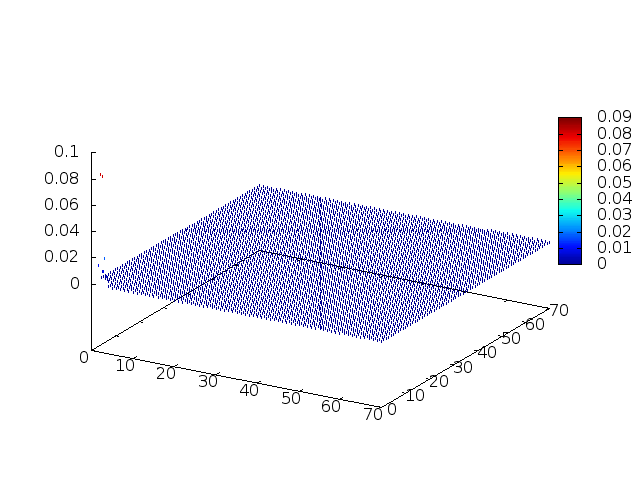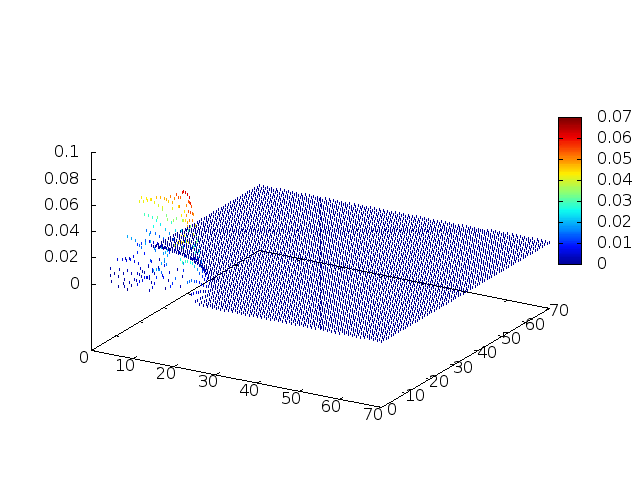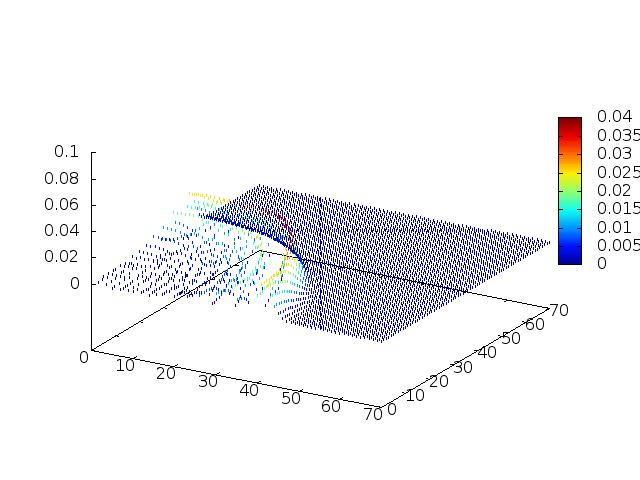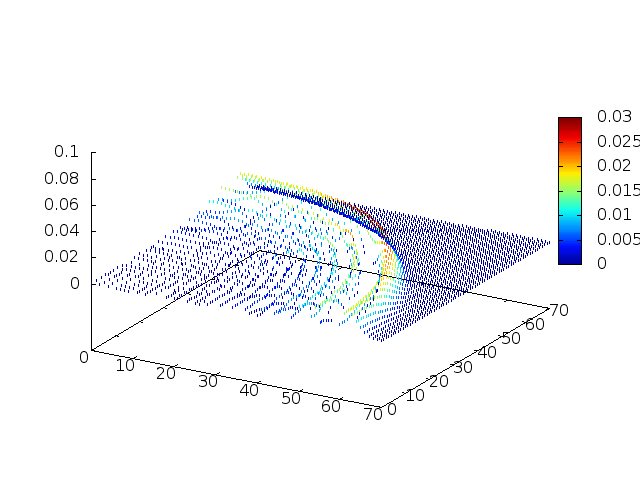
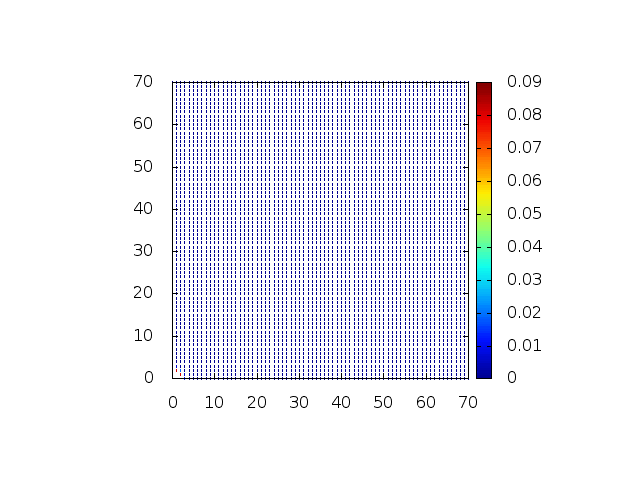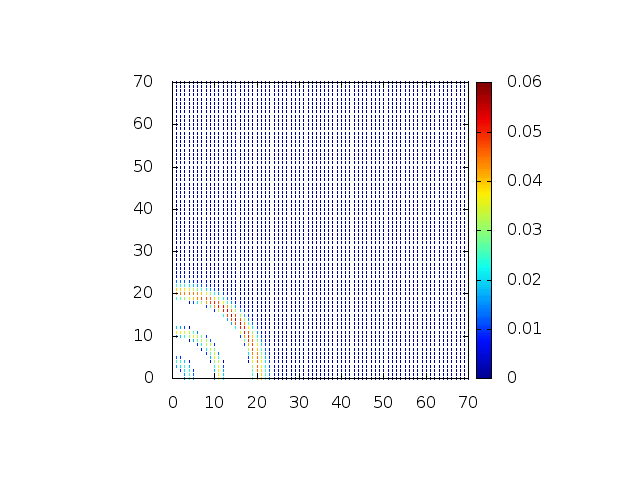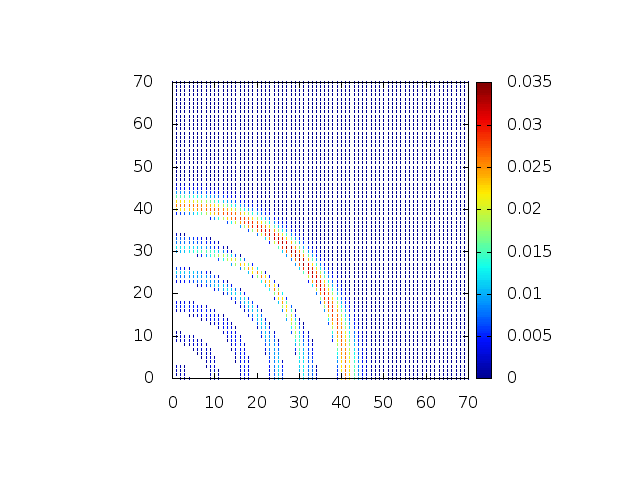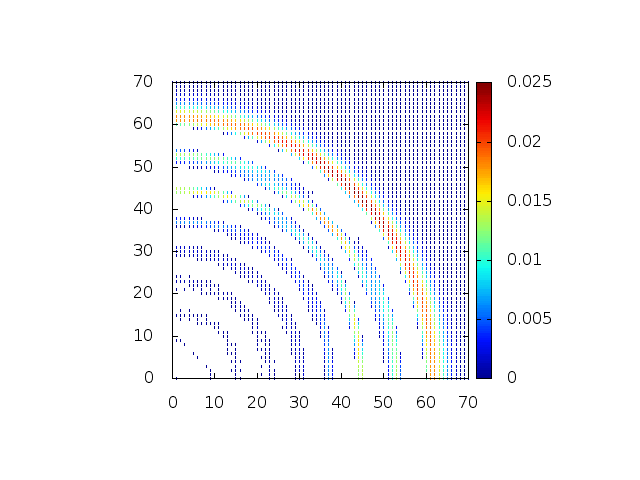
[[Arquivo:Grupo2_ondas1_ondaview.gif |frame|500px|center|Simulação em 2D de ondas em águas com profundidade constante, visão de cima]] | [[Arquivo:Grupo2_ondas1_ondaview.gif |frame|500px|center|Simulação em 2D de ondas em águas com profundidade constante, visão de cima]] | ||
[[Arquivo:Grupo2_ondas1_ondanormal.gif|frame|500px|center|Simulação em 2D de onda em águas com profundidade constante, visão em ângulo]] | [[Arquivo:Grupo2_ondas1_ondanormal.gif|frame|500px|center|Simulação em 2D de onda em águas com profundidade constante, visão em ângulo]] | ||
Podemos então, analisar como a mesma condição inicial se porta quando <math>H(x,y,t)</math> descreve uma gaussiana na origem: | |||
[[Arquivo:Grupo2_ondas1_ondaview_hsino.gif |frame|500px|center|Simulação em 2D de ondas em águas com gaussiana na origem, visão de cima]] | [[Arquivo:Grupo2_ondas1_ondaview_hsino.gif |frame|500px|center|Simulação em 2D de ondas em águas com gaussiana na origem, visão de cima]] | ||
Edição das 23h47min de 23 de outubro de 2017
Introdução
A modelagem numérica vem se tornando cada vez mais uma ferramenta indispensável para um engenheiro. Tal modelagem pode trazer informações importantes para entender como melhor abordar o desenvolvimento de um projeto, neste caso, um que envolva ondas. Nós, como futuros engenheiros físicos, pensamos em trazer um problema mais "concreto", de engenharia costeira e portuária, que pode ou não surgir em nossas vidas profissionais mas cujo método de solução certamente estará presente. Aqui será apresentado um modelo baseado em uma condição inicial e um perfil topográfico do local estudado que descreve a evolução temporal de uma onda.
Nos métodos a seguir faremos a seguinte separação na equação da onda, que é uma equação diferencial parcial de segunda ordem:
Admitindo :
Uma vez que os métodos citados abaixo são para equações de primeira ordem, é necessário separarmos a equação em um sistema de equações, fazendo a substituição e :
Algoritmos
Apresentaremos aqui três abordagens diferentes para a solução da equação diferencial parcial apresentada, e após, seus respectivos erros associados.
Método de Lax-Friedrichs
Esse método consiste em discretizar as equações no esquema FTCS, ou seja:
Aqui agora vamos unir todas as equações para que no programa possamos iterar apenas uma equação ao invés de 3.
Leap-Frog
Para v temos:
Para w temos:
Para u temos:
Juntando todas elas temos:
Método de Lax-Wendroff de Dois Passos
Juntando para w:
Análise de erros e estabilidade
A análise de erros se torna mais evidente durante a escolha do parâmetro k, onde k = dt/dx. Valores grandes trazem pouca acurácia, e valores pequenos necessitam de muito poder de computação (tempo e dinheiro). Trazemos problemas mais simplificados como um "guia" de escolha do parâmetro.
A partir do cálulo da solução analítica da equação da onda, podemos calcular quanto o valor obtido pelos métodos difere da solução real, o que leva a uma visualização do erro corrente em cada método de integração.
Podemos observar a ordem com que os erros crescem à medida que o parâmetro k se torna maior. Lembrando que os valores da constante são determinados pela discretização do espaço e do tempo.
- GRAFICO DAS ENERGIA X T*
Simulação de Propagação de Onda 2D Dependente de Topografia
O modelo mais simples parte da equação da onda [1], acrescentando o termo . ,
Sendo uma representação da profundidade em águas calmas. Em uma situação real, pode-se obtê-la por mapeamento eletrônico do terreno por sistema de sonar.
Como primeira abordagem visando uma análise em 2D, a integração da equação em 1D (mesmo sendo uma situação muito idealizada) já traz resultados interessantes. Podemos observar, por exemplo, que a amplitude da onda cresce perto da costa. Esta informação por si só ajuda na construção de proteção contra quebra de ondas, pois é obtido o tamanho que as mesmas atingem.
É importante notar o quão poderosa é a integração de equações parciais na vida de um engenheiro.
A dependência em de permite um modelo no qual o terreno se modifica com o tempo. Isto é, pode-se observar o efeito que o deslocamento de placas tectônicas, deslizamentos, e até explosões provocam no comportamento das ondas na costa de um país e o reconhecimento de áreas críticas.
Estendendo o algoritmo do Leap-Frog à situação 2D, obtemos, para uma dada condição inicial e , onde C é uma constante:
Podemos então, analisar como a mesma condição inicial se porta quando descreve uma gaussiana na origem:
Bibliografia
1"The Wave Equation in 1D and 2D," por Knut–Andreas Lie, Dept. of Informatics, University of Oslo; disponível em: [1]; Último acesso em 23/10/2017.
2"Digital terrain mapping of the underside of sea ice from a small AUV," por Wadhams, M. J. Doble; disponível em: DOI: 10.1029/2007GL031921 ; Último acesso em 23/10/2017.