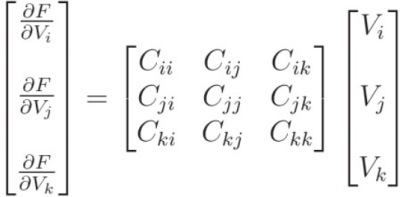Método de Elementos Finitos: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| (32 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
'''Grupo: Antônio Carlan, Gabriela Pereira, Renan Soares e Victor Gandara''' | '''Grupo: Antônio Carlan, Gabriela Pereira, Renan Soares e Victor Gandara''' | ||
| Linha 12: | Linha 10: | ||
Este é um método numérico de resolução aproximada para problemas de valores sobre contorno em equações diferenciais. É largamente utilizado na industrial para o desenvolvimento de novas tecnologias e produtos, pode ser utilizado tanto no processo de desenvolvimento quanto de otimização, através da simulação da física de situações em que se espera que o projeto atue. | Este é um método numérico de resolução aproximada para problemas de valores sobre contorno em equações diferenciais. É largamente utilizado na industrial para o desenvolvimento de novas tecnologias e produtos, pode ser utilizado tanto no processo de desenvolvimento quanto de otimização, através da simulação da física de situações em que se espera que o projeto atue. | ||
[ | [[Arquivo:FAE visualization.jpg|400px|thumb|center| Simulação de deformação de um veiculo https://en.wikipedia.org/wiki/Finite_element_method]] | ||
Simulação de deformação de um veiculo https://en.wikipedia.org/wiki/Finite_element_method | |||
[ | O que torna este método diferente é a forma com que ele discretiza e faz suas aproximações. Sua discretização é feita na geometria, ou seja, repartindo o objeto em diversos elementos menores. Desta forma é possível que se resolva problemas em geometrias complexas cuja solução analítica é desconhecida e que seriam muito difíceis com outros métodos. Também permite trabalhar de maneira simples com materiais compostos, ou de diferentes densidades em um objeto, uma vez que podemos definir tais propriedades individualmente para cada elemento. | ||
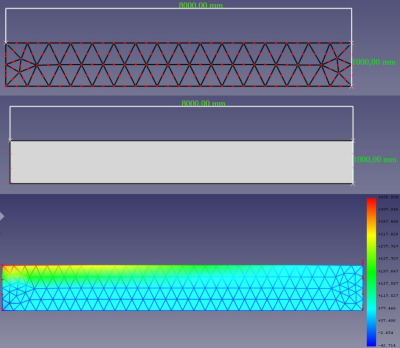
Modelo normal e modelo discretizado e representado por uma malha | |||
[[Arquivo:Exemplo inicio .png|400px|thumb|center| Modelo normal e modelo discretizado e representado por uma malha e simulação de estresse sofrido no objeto.]] | |||
=== O Método === | === O Método === | ||
| Linha 39: | Linha 34: | ||
Ela é composta por um conjunto de pontos interligados que descrevem o objeto. Estes pontos são chamados de '''nós''' e a união destes nós forma um elemento, e a união destes elementos formam o objeto que é nosso domínio. | Ela é composta por um conjunto de pontos interligados que descrevem o objeto. Estes pontos são chamados de '''nós''' e a união destes nós forma um elemento, e a união destes elementos formam o objeto que é nosso domínio. | ||
[ | [[Arquivo:Nos.png|400px|thumb|center| Malha composta por elementos que são compostos por nós.]] | ||
# '''Dimensão:''' A malha pode ser unidimensional, bidimensional ou tridimensional. | # '''Dimensão:''' A malha pode ser unidimensional, bidimensional ou tridimensional. | ||
[ | [[Arquivo:Print slide 5.png|400px|thumb|center| Malha composta por elementos que são compostos por nós.]] | ||
# '''Ordem:''' Quanto maior a ordem da malha mais precisa será a aproximação dos resultados entre os nós, porém aumenta o consumo computacional. | # '''Ordem:''' Quanto maior a ordem da malha mais precisa será a aproximação dos resultados entre os nós, porém aumenta o consumo computacional. | ||
# '''Densidade de elementos:''' Pode-se escolher por gerar uma malha mais ou menos detalhada, isso implica no consumo computacional. Quanto mais detalhada a malha, ou seja, quanto maior o numero de nós da malha, menor será o erro de aproximação do problema real. | # '''Densidade de elementos:''' Pode-se escolher por gerar uma malha mais ou menos detalhada, isso implica no consumo computacional. Quanto mais detalhada a malha, ou seja, quanto maior o numero de nós da malha, menor será o erro de aproximação do problema real. | ||
[ | [[Arquivo:Densidade de malha.png|400px|thumb|center| Discretização de uma área utilizando o software GMSH com diferentes padrões gerando duas malhas com diferentes densidades de nós.]] | ||
=== Funcionamento do método === | === Funcionamento do método === | ||
Cada nó desta malha terá atribuída uma variável do problema físico que esta sendo implementado(o valor da grandeza contínua para aquele ponto), como Tensão Elétrica, Dilatação, Temperatura, etc. Esta variável é chamada '''Valor nodal''', ela representa a solução da equação naquele ponto (Variáveis nodais = incógnitas ou graus de liberdade do problema). | Cada nó desta malha terá atribuída uma variável do problema físico que esta sendo implementado(o valor da grandeza contínua para aquele ponto), como Tensão Elétrica, Dilatação, Temperatura, etc. Esta variável é chamada '''Valor nodal''', ela representa a solução da equação naquele ponto (Variáveis nodais = incógnitas ou graus de liberdade do problema). | ||
[[Arquivo:Slide7.png|400px|thumb|center|]] | |||
[ | |||
Já a grandeza contínua é aproximada em cada elemento por um '''polinômio''' que é definido usando os valores nodais da grandeza. Ou seja, nós iremos descobrir os valores nodais dos nós e entre eles,os valores da grandeza contínua serão dados por uma aproximação polinomial. | Já a grandeza contínua é aproximada em cada elemento por um '''polinômio''' que é definido usando os valores nodais da grandeza. Ou seja, nós iremos descobrir os valores nodais dos nós e entre eles,os valores da grandeza contínua serão dados por uma aproximação polinomial. | ||
| Linha 66: | Linha 60: | ||
Os valores nodais, que são nossas incógnitas, precisam ser isolados e deixados em função das coordenadas dos nós, que possuímos através da malha de elementos finitos já gerada. | Os valores nodais, que são nossas incógnitas, precisam ser isolados e deixados em função das coordenadas dos nós, que possuímos através da malha de elementos finitos já gerada. | ||
[ | [[Arquivo:Slide9.png|400px|thumb|center|]] | ||
<math> V_1 e V_2 </math> -> valores nodais | <math> V_1 e V_2 </math> -> valores nodais | ||
| Linha 88: | Linha 82: | ||
logo: | logo: | ||
<center><math> | <center><math> | ||
| Linha 107: | Linha 99: | ||
\end{bmatrix} | \end{bmatrix} | ||
</math></center> | </math></center> | ||
| Linha 131: | Linha 123: | ||
Esta fica conhecida por aproximação nodal pois a grandeza <math> V(x) </math> pode ser obtida em qualquer ponto do intervalo <math> [x_1, x_2] </math> a partir dos valores <math> V_1 </math> e <math> V_2 </math>. | Esta fica conhecida por aproximação nodal pois a grandeza <math> V(x) </math> pode ser obtida em qualquer ponto do intervalo <math> [x_1, x_2] </math> a partir dos valores <math> V_1 </math> e <math> V_2 </math>. | ||
===== Função Interpolação ===== | |||
Esta aproximação nodal pode ainda ser reescrita como: | |||
:<math> | |||
V(x) = \phi_1{(x)}V_1 + \phi_2{(x)}V_2 | |||
</math> | |||
Com: | |||
<math> | |||
\phi_1{(x)} = \frac{x_2 - x}{L} | |||
</math> | |||
e | |||
<math> | |||
\phi_2{(x)} = \frac{x - x_1}{L} | |||
</math> | |||
sendo <math> L = x_2 - x_1 </math> | |||
As funções <math>\phi_1{(x)}</math> e <math>\phi_2{(x)}</math> são conhecidas como '''funções de interpolação''' e são responsáveis por fazer com que cada nó do elemento contribua com uma parte do valor resultante em qualquer ponto dentro do elemento. | |||
E devido a propriedade do delta de Kronecker, vista abaixo, é garantido que as equações só terão valor entre os nós dentro do elemento que são definidos: | |||
:<math> | |||
\phi_i{(x_j)} =\left\{\begin{array}{lc} 1, \quad \text{se}\quad i=j\\ | |||
0, \quad \text{se} \quad i \ne j \end{array}\right. | |||
</math> | |||
Então, por exemplo, nossa equação para o elemento 1, no caso visto aqui de 1D, para um problema de tensão, fica: | |||
Elemento 1: | |||
:<math> | |||
V^{(1)} (x) = \phi_1^{(1)}(x) V_1 \phi_2^{(1)}(x) V_2 | |||
</math> | |||
Com: | |||
<math> | |||
\phi_1^{(1)}{(x)} = \frac{x_2 - x}{x_2 - x_1} | |||
</math> | |||
e | |||
<math> | |||
\phi_2^{(1)}{(x)} = \frac{x - x_1}{x_2 - x_1} | |||
</math> | |||
Fica fácil perceber que os valores nodais dos dois nós se interpolam e contribuem para os valores entre para o resultado. | |||
A notação geral da função interpolação fica: | |||
:<math> | |||
\phi_i^{(e)} (x) | |||
</math> | |||
Em que: <math> (e) = elemento </math> e <math> i = nó </math> | |||
As funções são diferentes para cada elemento e elas são nulas fora do elemento a que pertencem. | |||
Também existem a função chapéu, que é outro tipo de interpolação. | |||
==== Solução Global ==== | |||
Seguindo com o caso do problema de tensão elétrica, a solução global será dada pelo somatório das funções de interpolação de cada elemento. | |||
:<math> | |||
V_ex (x) \cong V(x) - \sum_{e=1}^{N_{elem}} V^{(e)} (x) | |||
</math> | |||
Até aqui nós chegamos a essa equação partindo da premissa que temos os valores nodais, fizemos isso apenas para explicar como os valores nodas e suas interpolações se comportam na malha. | |||
Porém os valores nodais são as nossas incógnitas e são eles quem queremos descobrir, a interpolação será a predição dos valores entre os valores nodais. | |||
Como visto, no MEF cada elemento terá suas próprias equações baseadas nos seus valores nodais e nas coordenadas destes valores. Para de fato introduzir o problema físico precisamos da forma fraca dele, já que é a partir da forma fraca que chegaremos no sistema de equações que nos permite obter os valores nodais | |||
===== Forma Fraca ===== | |||
Quando se tem uma problema envolvendo um operador diferencial, é possível usar o que se conhece por forma fraca do operador, que nada mais é que a representação integral do problema, a qual já engloba/explicita as condições de contorno e utiliza-se o método de resíduos ponderados para isso. | |||
Para a construção da forma fraca nós podemos escolher uma função arbitrária w(x) e multiplicá-la pela forma forte, que é a equação diferencial original que descreve o problema, e pela condição de contorno em x=0. Em sequência nós integramos ambas dentro do domínio onde elas foram definidas. Como w(x) é uma função arbitrária que pode ser qualquer função, ela força a solução, já que qualquer coisa multiplicada por ela tem que ser 0. | |||
Para entender esse método, nós podemos olhar o problema de uma barra elástica carregada axialmente. | |||
Imagem.jpg | |||
[[Arquivo:Imagem.jpg|400px|thumb|center|]] | |||
Considerando que a barra está em equilíbrio, nós podemos representar a relação entre as forças internas p(x) e as externas b(x) por essa equação | |||
:<math> | |||
-p(x) + b (x + \frac{\Delta x}{2}) \Delta_x + p(x + \Delta_x) = 0 | |||
</math> | |||
Reorganizando e tomando o limite quando <math>\Delta_x</math> tende a 0 nós chegamos em uma equação diferencial para descrever esse problema. | |||
:<math> | |||
\frac{p(x + \Delta_x) - p(x)}{\Delta_x} + b (x + \frac{\Delta_x}{2}) = 0 | |||
</math> | |||
No entanto, ela está em termos das forças internas. Para reescrever isso, basta lembrar que a tensão é definida como a força pela área da seção transversal e, pela lei de tensão deformação para um material elástico linear, nós temos que | |||
:<math> | |||
\sigma = E_(x) \varepsilon_(x) | |||
</math> | |||
onde E é o módulo de young e épsilon é a deformação, definida como | |||
:<math> | |||
\varepsilon_(x)= \frac{u(x + \Delta_x) - u(x)}{\Delta_x} | |||
</math> | |||
Então, lembrando também da definição de derivada, eu posso reescrever a equação para esse problema como | |||
:<math> | |||
\frac{d}{dx} (AE \frac{du}{dx}) +b = 0 | |||
</math> | |||
E, para resolver essa equação, precisamos das condições de contorno, as quais podemos tomar como sendo | |||
:<math> | |||
\sigma(0) = (E \frac{du}{dx})_{x=0} = \frac{p(0)}{A(0)} \equiv -\tau | |||
</math> | |||
<math> | |||
u(l)= u | |||
</math> | |||
relembrando que u(x) é a função que representa o deslocamento do corpo, ou seja, a deformação. | |||
Agora, para obter a forma fraca, eu multiplico e integro a equação diferencial e a condição de contorno que diz respeito a tensão | |||
:<math> | |||
\int w (\frac{d}{dx} (AE \frac{du}{dx}) +b)dx=0 | |||
</math> | |||
:<math> | |||
w A(E\frac{du}{dx} + \tau)=0 | |||
</math> | |||
Aqui vale notar que a integral da condição de contorno foi substituída pela multiplicação pela área, já que o domínio dessa condição de contorno é a área da seção transversal mas só em x=0, ou seja, ela age só em um ponto | |||
Agora, utilizando a definição de integração por partes, eu consigo escrever | |||
:<math> | |||
\int_{0}^{l} w\frac{d}{dx} (AE \frac{du}{dx})dx = (wA \tau)|_{0}^{l} - \int_{0}^{l} \frac{dw}{dx} AE \frac{du}{dx}dx | |||
</math> | |||
Olhando pra esse termo e para a equação da condição de contorno mostrada anteriormente, e lembrando da definição de sigma, eu vejo que eu posso reescrever essa equação integral como | |||
:<math> | |||
\int_{0}^{l} \frac{dw}{dx} AE \frac{du}{dx} dx= (wA \tau)_{x=0} + \int_{0}^{l} wb dx | |||
</math> | |||
que é a forma fraca da equação diferencial que descreve o nosso problema | |||
Qualquer solução que satisfizer a forma fraca, com w(l)=0 e u(l)=u também será solução da equação diferencial original do nosso problema | |||
Alternativamente, podemos encontrar a forma fraca através da minimização de um funcional dentro de um espaço de funções válido para o nosso problema e suas condições de contorno. A obtenção desse funcional não é um processo trivial, mas quando se trata de problemas físicos, esse funcional coincide com a energia do sistema, sendo, por exemplo, a energia potencial elástica do sólido para problemas de mecânica dos sólidos e a energia eletrostática armazenada na região de cálculo para problemas eletrostáticos sem carga livre no domínio de estudo. A função que minimiza essa energia é a solução do problema original. Como discretizamos o problema, devemos minimizar o funcional com relação a cada nó. Se eu tenho 10 nós vou ter 10 equações (derivadas igualadas a 0) para minimizar o funcional nos 10 nós. | |||
Podemos usar um problema eletrostático sem cargas livres para exemplificar esse método, conhecido como Método Variacional. Tomando as equações de Maxwell temos, então: | |||
:<math> | |||
\nabla . \vec{D} = \rho | |||
</math> | |||
:<math> | |||
\vec{E} = - \nabla V | |||
</math> | |||
:<math> | |||
\vec{D} = \epsilon \vec{E} | |||
</math> | |||
:<math> | |||
\nabla ^2 V = - \frac{\rho}{\epsilon} | |||
</math> | |||
:<math> | |||
\nabla ^2 V = 0 | |||
</math> | |||
A equação que rege esse problema eletrostático é a equação de laplace, e em um problema 2D fica: | |||
:<math> | |||
\frac{\partial^2 {V}}{\partial x^2} + \frac{\partial^2 {V}}{\partial y^2} = 0 | |||
</math> | |||
Obtém-se, então, uma equação funcional associada à energia do sistema | |||
:<math> | |||
F = \int_{\omega} \frac{1}{2} E^2 d\omega | |||
</math> | |||
Pelo método variacional, eu satisfaço a equação de laplace quando a energia armazenada no sistema, que é o meu funcional, for mínima. Como analisamos elemento por elemento, podemos dizer que o funcional vai ser constante dentro de um elemento, e tem que ser minimizado | |||
dentro desse elemento, para tal, eu minimizo o funcional com relação a cada nó do elemento, o que me leva a um conjunto de equações que podemos organizar no que se conhece como matriz elementar, se eu tenho 3 nós em cada elemento vou ter uma matriz 3 por 3. | |||
Podemos escrever a derivada total do funcional como a soma da derivada em cada elemento, onde <math>F^e</math> é o valor do funcional em cada elemento | |||
:<math> | |||
\frac{\partial{F^{(e)}}}{\partial{V_n}} = \sum_{e=1}^{M} \frac{\partial F^e}{\partial V_n} = 0 | |||
</math> | |||
onde, | |||
:<math> | |||
\frac{\partial{F^{(e)}}}{\partial{V_n}} = \frac{\partial}{\partial V_n} \int_{e}^{} \frac{1}{2} \varepsilon^{(e)} E^2 d\Omega | |||
</math> | |||
Se consideramos a permissividade e o campo elétrico constante em cada elemento, eles podem sair da integral. A integral de <math>\Omega</math> no elemento é a área do elemento, que é o determinante (D) dividido por 2, com isso, obtemos que: | |||
:<math> | |||
\frac{\partial{F^{(e)}}}{\partial{V_n}} = \frac{\partial}{\partial V_n} [ \frac{1}{2} \varepsilon^{(e)} E^2 \int_{e} d\Omega] = \frac{1}{2} \varepsilon^{(e)} \frac{D \partial{E^2}}{2 \partial{V_n}} | |||
</math> | |||
utilizando elementos triangulares e interpolação linear 2D, podemos escrever a derivada segunda do campo elétrico como: | |||
:<math> | |||
\frac{\partial E^2}{\partial V_1} = \frac{2}{D^2} [(q_1 V_1 + q_2 V_2 + q_3 V_3)q_1 + (r_1 V_1 + r_2 V_2 + r_3 V_3)r_1 | |||
</math> | |||
Com isso, eu posso escrever a matriz elementar como: | |||
[[Arquivo:Matriz elementar.png|400px|thumb|center|]] | |||
:<math> | |||
C_{ij} = \frac{\epsilon}{2Det} (q_i q_j + r_i r_j) | |||
</math> | |||
Mas eu preciso minimizar o funcional em todos os elementos, então a contribuição de cada elemento deve ser inserida na matriz global - MXM - sendo M o número de nós. Na matriz global nós somamos os termos dos nós que se interseccionam em diferentes elementos. É preciso de duas condições de contorno (valores para 2 nós), substituindo elas na matriz global eu consigo calcular os valores para os nós que eu desconheço. Depois de resolver os valores para os nós, eu consigo determinar a solução em qualquer ponto do domínio. | |||
[[Arquivo:Contribuição elemento.png|400px|thumb|center|]] | |||
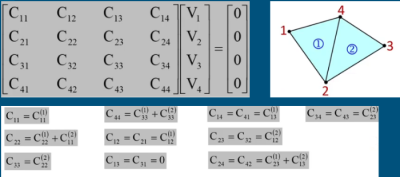
Um exemplo de como ficaria a matriz global e seus elementos para uma determinada malha: | |||
[[Arquivo:Matrizglobal.png|400px|thumb|center|]] | |||
Por fim tendo a matriz global determinada e com as condições de contorno aplicadas, sua resolução trará enfim a solução do problema pelo método de elementos finitos. | |||
=== Programas CAE === | |||
Na engenharia este método é largamente aplicado, porém raramente utilizado desta forma, criando a matriz manualmente e os programas para solução do método. Existem programas que estão a décadas sendo aperfeiçoados, alguns proprietários como o CONSOL, e outros livres como OpenFOAM, Calcuix, ElmerFEM, entre outros. | |||
A implementação do MEF em projetos costuma seguir um workflow assim: | |||
# Desenho do modelo 3D que deseja estudar. | |||
# Transformar este modelo em uma malha, no formato que os programas de elementos finitos reconhecem. | |||
# Indicar o problema físico a ser estudado e suas condições iniciais aplicadas ao modelo 3D. | |||
# Rodar o programa adequado para o problema. | |||
# Utilizar de programas para examinar os resultados. | |||
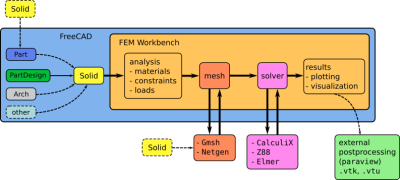
Como pode-se ver no diagrama abaixo também: | |||
[[Arquivo:FEM Workbench workflow.png|400px|thumb|center| Workflow no FreeCAD - https://wiki.freecadweb.org/FEM_Workbench]] | |||
Edição atual tal como às 09h46min de 26 de outubro de 2021
Grupo: Antônio Carlan, Gabriela Pereira, Renan Soares e Victor Gandara
Objetivo: Apresentar uma introdução do Método de Elementos Finitos, abordando seu funcionamento e demonstrando suas etapas através de um exemplo, demonstrando seu potencial e o que o diferencia de outros métodos estudados nas cadeiras de métodos computacionais até então vistos.
Introdução ao Método de Elementos Finitos(MEF)
Aplicação
Este é um método numérico de resolução aproximada para problemas de valores sobre contorno em equações diferenciais. É largamente utilizado na industrial para o desenvolvimento de novas tecnologias e produtos, pode ser utilizado tanto no processo de desenvolvimento quanto de otimização, através da simulação da física de situações em que se espera que o projeto atue.

O que torna este método diferente é a forma com que ele discretiza e faz suas aproximações. Sua discretização é feita na geometria, ou seja, repartindo o objeto em diversos elementos menores. Desta forma é possível que se resolva problemas em geometrias complexas cuja solução analítica é desconhecida e que seriam muito difíceis com outros métodos. Também permite trabalhar de maneira simples com materiais compostos, ou de diferentes densidades em um objeto, uma vez que podemos definir tais propriedades individualmente para cada elemento.
O Método
O conceito fundamental do MEF é a aproximação de uma quantidade continua(p. ex., tensão elétrica, temperatura, etc.) através de um modelo discreto composto por um conjunto de funções simples que são definidas em um número finito de subdomínios(elementos)
A resolução de um problema através do MEF envolve quatro etapas principais:
- Discretização da região: Transformar o objeto de estudo em vários elementos menores que juntos formam o objeto original de forma aproximada e a isso chama-se Malha.
- Aproximação da solução: Obtenção das equações correspondentes de cada elemento, através de interpolação polinomial.
- Montagem do sistema global: Juntar os elementos e suas equações em uma matriz que fornecerá a solução global.
- Resolução do sistema: Resolver a matriz gerada para obter a solução aproximada do problema.
Discretização: A Malha
A malha define o domínio do problema, ela é a base do método. Porém não é parte do algoritmo em si. Normalmente é criada automaticamente por um programa especifico para isso, como GMSH e NetGen. Apenas sendo fornecida as especificações que se deseja para a malha, vão influenciar na quantidade de nós, na dimensão do domínio e na precisão da aproximação.
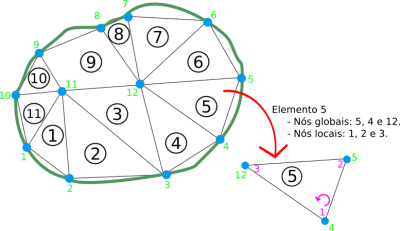
Ela é composta por um conjunto de pontos interligados que descrevem o objeto. Estes pontos são chamados de nós e a união destes nós forma um elemento, e a união destes elementos formam o objeto que é nosso domínio.
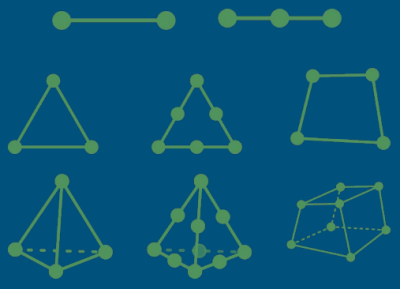
- Dimensão: A malha pode ser unidimensional, bidimensional ou tridimensional.
- Ordem: Quanto maior a ordem da malha mais precisa será a aproximação dos resultados entre os nós, porém aumenta o consumo computacional.
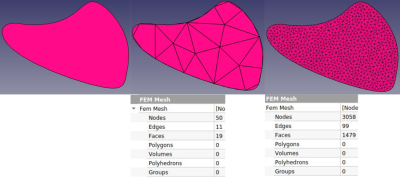
- Densidade de elementos: Pode-se escolher por gerar uma malha mais ou menos detalhada, isso implica no consumo computacional. Quanto mais detalhada a malha, ou seja, quanto maior o numero de nós da malha, menor será o erro de aproximação do problema real.
Funcionamento do método
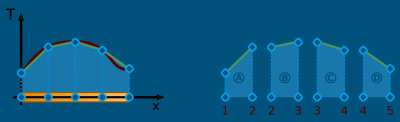
Cada nó desta malha terá atribuída uma variável do problema físico que esta sendo implementado(o valor da grandeza contínua para aquele ponto), como Tensão Elétrica, Dilatação, Temperatura, etc. Esta variável é chamada Valor nodal, ela representa a solução da equação naquele ponto (Variáveis nodais = incógnitas ou graus de liberdade do problema).
Já a grandeza contínua é aproximada em cada elemento por um polinômio que é definido usando os valores nodais da grandeza. Ou seja, nós iremos descobrir os valores nodais dos nós e entre eles,os valores da grandeza contínua serão dados por uma aproximação polinomial.
Lembrando que os elementos são formados pelos nós e que os valores nodais estão associado aos nós e não ao elemento diretamente.
Então, cada elemento terá um polinômio que descreve a grandeza contínua na região entre os nós que formam este elemento, no caso de uma matriz com elementos de primeira ordem, será uma reta entre os valores nodais. Os polinômios são escolhidos/deduzidos de forma que a continuidade seja mantida na fronteira entre os elementos, utilizando os métodos matemáticos adequados para isso.
"Este polinômio resulta de um ajuste dos valores nodais para que se tenha uma boa aproximação da grandeza real, este ajuste é feito através da minimização de alguma grandeza associada ao problema."
Interpolação
Os valores nodais, que são nossas incógnitas, precisam ser isolados e deixados em função das coordenadas dos nós, que possuímos através da malha de elementos finitos já gerada.
-> valores nodais -> coordenadas dos nós
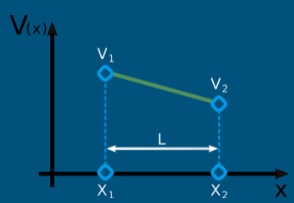
Aproximação polinomial no caso da malha de primeira ordem:
As variáveis a1 e a2 são coeficientes da interpolação, porém não as temos e não queremos deixa-las no calculo, para isso:
logo:
Portanto:
Substituindo os valores de e na equação de interpolação anterior ficaremos com:
Ou, como é definido a aproximação nodal:
Esta fica conhecida por aproximação nodal pois a grandeza pode ser obtida em qualquer ponto do intervalo a partir dos valores e .
Função Interpolação
Esta aproximação nodal pode ainda ser reescrita como:
Com:
e
sendo
As funções e são conhecidas como funções de interpolação e são responsáveis por fazer com que cada nó do elemento contribua com uma parte do valor resultante em qualquer ponto dentro do elemento.
E devido a propriedade do delta de Kronecker, vista abaixo, é garantido que as equações só terão valor entre os nós dentro do elemento que são definidos:
Então, por exemplo, nossa equação para o elemento 1, no caso visto aqui de 1D, para um problema de tensão, fica:
Elemento 1:
Com:
e
Fica fácil perceber que os valores nodais dos dois nós se interpolam e contribuem para os valores entre para o resultado.
A notação geral da função interpolação fica:
Em que: e Falhou ao verificar gramática (erro de sintaxe): {\displaystyle i = nó }
As funções são diferentes para cada elemento e elas são nulas fora do elemento a que pertencem.
Também existem a função chapéu, que é outro tipo de interpolação.
Solução Global
Seguindo com o caso do problema de tensão elétrica, a solução global será dada pelo somatório das funções de interpolação de cada elemento.
Até aqui nós chegamos a essa equação partindo da premissa que temos os valores nodais, fizemos isso apenas para explicar como os valores nodas e suas interpolações se comportam na malha.
Porém os valores nodais são as nossas incógnitas e são eles quem queremos descobrir, a interpolação será a predição dos valores entre os valores nodais.
Como visto, no MEF cada elemento terá suas próprias equações baseadas nos seus valores nodais e nas coordenadas destes valores. Para de fato introduzir o problema físico precisamos da forma fraca dele, já que é a partir da forma fraca que chegaremos no sistema de equações que nos permite obter os valores nodais
Forma Fraca
Quando se tem uma problema envolvendo um operador diferencial, é possível usar o que se conhece por forma fraca do operador, que nada mais é que a representação integral do problema, a qual já engloba/explicita as condições de contorno e utiliza-se o método de resíduos ponderados para isso.
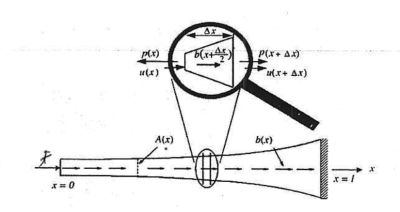
Para a construção da forma fraca nós podemos escolher uma função arbitrária w(x) e multiplicá-la pela forma forte, que é a equação diferencial original que descreve o problema, e pela condição de contorno em x=0. Em sequência nós integramos ambas dentro do domínio onde elas foram definidas. Como w(x) é uma função arbitrária que pode ser qualquer função, ela força a solução, já que qualquer coisa multiplicada por ela tem que ser 0. Para entender esse método, nós podemos olhar o problema de uma barra elástica carregada axialmente. Imagem.jpg
Considerando que a barra está em equilíbrio, nós podemos representar a relação entre as forças internas p(x) e as externas b(x) por essa equação
Reorganizando e tomando o limite quando tende a 0 nós chegamos em uma equação diferencial para descrever esse problema.
No entanto, ela está em termos das forças internas. Para reescrever isso, basta lembrar que a tensão é definida como a força pela área da seção transversal e, pela lei de tensão deformação para um material elástico linear, nós temos que
onde E é o módulo de young e épsilon é a deformação, definida como
Então, lembrando também da definição de derivada, eu posso reescrever a equação para esse problema como
E, para resolver essa equação, precisamos das condições de contorno, as quais podemos tomar como sendo
relembrando que u(x) é a função que representa o deslocamento do corpo, ou seja, a deformação.
Agora, para obter a forma fraca, eu multiplico e integro a equação diferencial e a condição de contorno que diz respeito a tensão
Aqui vale notar que a integral da condição de contorno foi substituída pela multiplicação pela área, já que o domínio dessa condição de contorno é a área da seção transversal mas só em x=0, ou seja, ela age só em um ponto
Agora, utilizando a definição de integração por partes, eu consigo escrever
Olhando pra esse termo e para a equação da condição de contorno mostrada anteriormente, e lembrando da definição de sigma, eu vejo que eu posso reescrever essa equação integral como
que é a forma fraca da equação diferencial que descreve o nosso problema
Qualquer solução que satisfizer a forma fraca, com w(l)=0 e u(l)=u também será solução da equação diferencial original do nosso problema
Alternativamente, podemos encontrar a forma fraca através da minimização de um funcional dentro de um espaço de funções válido para o nosso problema e suas condições de contorno. A obtenção desse funcional não é um processo trivial, mas quando se trata de problemas físicos, esse funcional coincide com a energia do sistema, sendo, por exemplo, a energia potencial elástica do sólido para problemas de mecânica dos sólidos e a energia eletrostática armazenada na região de cálculo para problemas eletrostáticos sem carga livre no domínio de estudo. A função que minimiza essa energia é a solução do problema original. Como discretizamos o problema, devemos minimizar o funcional com relação a cada nó. Se eu tenho 10 nós vou ter 10 equações (derivadas igualadas a 0) para minimizar o funcional nos 10 nós.
Podemos usar um problema eletrostático sem cargas livres para exemplificar esse método, conhecido como Método Variacional. Tomando as equações de Maxwell temos, então:
A equação que rege esse problema eletrostático é a equação de laplace, e em um problema 2D fica:
Obtém-se, então, uma equação funcional associada à energia do sistema
Pelo método variacional, eu satisfaço a equação de laplace quando a energia armazenada no sistema, que é o meu funcional, for mínima. Como analisamos elemento por elemento, podemos dizer que o funcional vai ser constante dentro de um elemento, e tem que ser minimizado dentro desse elemento, para tal, eu minimizo o funcional com relação a cada nó do elemento, o que me leva a um conjunto de equações que podemos organizar no que se conhece como matriz elementar, se eu tenho 3 nós em cada elemento vou ter uma matriz 3 por 3. Podemos escrever a derivada total do funcional como a soma da derivada em cada elemento, onde é o valor do funcional em cada elemento
onde,
Se consideramos a permissividade e o campo elétrico constante em cada elemento, eles podem sair da integral. A integral de no elemento é a área do elemento, que é o determinante (D) dividido por 2, com isso, obtemos que:
utilizando elementos triangulares e interpolação linear 2D, podemos escrever a derivada segunda do campo elétrico como:
Com isso, eu posso escrever a matriz elementar como:
Mas eu preciso minimizar o funcional em todos os elementos, então a contribuição de cada elemento deve ser inserida na matriz global - MXM - sendo M o número de nós. Na matriz global nós somamos os termos dos nós que se interseccionam em diferentes elementos. É preciso de duas condições de contorno (valores para 2 nós), substituindo elas na matriz global eu consigo calcular os valores para os nós que eu desconheço. Depois de resolver os valores para os nós, eu consigo determinar a solução em qualquer ponto do domínio.
Um exemplo de como ficaria a matriz global e seus elementos para uma determinada malha:
Por fim tendo a matriz global determinada e com as condições de contorno aplicadas, sua resolução trará enfim a solução do problema pelo método de elementos finitos.
Programas CAE
Na engenharia este método é largamente aplicado, porém raramente utilizado desta forma, criando a matriz manualmente e os programas para solução do método. Existem programas que estão a décadas sendo aperfeiçoados, alguns proprietários como o CONSOL, e outros livres como OpenFOAM, Calcuix, ElmerFEM, entre outros.
A implementação do MEF em projetos costuma seguir um workflow assim:
- Desenho do modelo 3D que deseja estudar.
- Transformar este modelo em uma malha, no formato que os programas de elementos finitos reconhecem.
- Indicar o problema físico a ser estudado e suas condições iniciais aplicadas ao modelo 3D.
- Rodar o programa adequado para o problema.
- Utilizar de programas para examinar os resultados.
Como pode-se ver no diagrama abaixo também:











![{\displaystyle V(x)={\frac {1}{L}}[V_{1}x_{2}-V_{2}x_{1}+(V_{2}-V_{1})x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/267f51e999cb87e75ec4fdbf6542883347a59fa4)


![{\displaystyle [x_{1},x_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91bdff343d848c2b70c68b5c04a2479b14a9fef0)





































![{\displaystyle {\frac {\partial {F^{(e)}}}{\partial {V_{n}}}}={\frac {\partial }{\partial V_{n}}}[{\frac {1}{2}}\varepsilon ^{(e)}E^{2}\int _{e}d\Omega ]={\frac {1}{2}}\varepsilon ^{(e)}{\frac {D\partial {E^{2}}}{2\partial {V_{n}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e7218e264ba6bd9968644b83563c5a206b6f417)