Problema de Fermi-Pasta-Ulam

Grupo: Augusto M Giani e Henrique Padovani

O objetivo deste trabalho é replicar os resultados do problema proposto por Fermi-Pasta-Ulam em 1953 sobre sistemas dinâmicos não lineares. As análises serão sobre a solução dos modos de vibração comparados à solução analítica para poucas massas e também sobre a energia do sistema para os modos de oscilação, enquanto o sistema evolui no tempo.

O Problema

O Problema proposto constitui-se de simulações em uma rede de partículas ligadas entre si através de molas que obedecem a Lei de Hooke com uma correção não-linear quadrática ou cúbica

• 

  Figura 1. Problema de Fermi-Pasta-Ulam, molas acopladas.

A lei de forças que rege o comportamento deste sistema é:

$F=-k\Delta x-\alpha k\Delta x^{2}-\beta k\Delta x^{3}$.

Onde $\Delta x$ e a deformação a cada 2 massas acopladas ($x_{i+1}-x_{i}$), $k$ é a constante elástica da mola, $\alpha$ é um parâmetro de deformação arbitrário que controla a correção não linear quadrática e $\beta$ é o parâmetro que controla a correção cúbica. Importante ressaltar que se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha } é possuir assumir um valor não nulo, real, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta } é igual a zero no nosso sistema, ou vice-versa. Não estamos analisando correções quadráticas somadas com correções cúbicas neste trabalho.

Motivação: O que era esperado e o paradoxo XXX

Escrever a motivação ...

Discretização

A discretização deste problema gira em torno de abrir a equação das forças, e com o termo de aceleração, iterar o movimento das partículas a partir disso . Partimos do problema com correção quadrática, ou seja, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = 0 } . Partindo de:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = -k \Delta x - \alpha k \Delta x^2 } ,

subtituímos pelas variáveis discretas:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m \ddot{x_j} = -k \left( (x_{j+1} - x_j) - (x_j - x_{j-1}) \right) - \alpha k \left( (x_{j+1} - x_j) - (x_j - x_{j-1}) \right) } ,

Chegamos em:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m \ddot{x_j} = k \left( x_{j+1} - 2x_{j} + x_{j-1} \right) \left[ 1 + \alpha \left( x_{j+1} - x_{j-1} \right) \right] }

Em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ddot{x_j} } é a aceleração da j-ésima partícula, com ela conseguimos integrar o movimento das partículas.

Implementação

Usamos XX partículas, com modo de oscilação YY

Resultados

SUBTITULOS

negrito, Simultaneous OverRelaxation

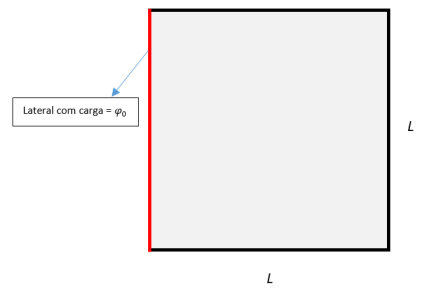
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \Phi(x = 0,y) = \Phi_{0} = 1 \\ \Phi(x = L,y) = \Phi(x,y = 0) = \Phi(x,y = L) = 0\\ \end{cases} }

• 

  Problema da borda carregada eletricamente.
• 

  Gráfico da solução analítica somando até o termo n=199.

### Exemplo da evolução temporal no método de relaxação ###
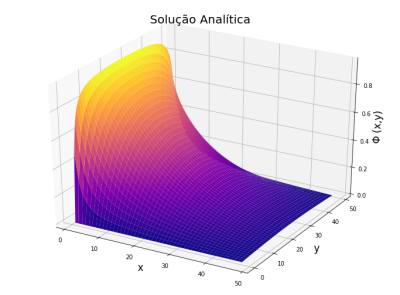
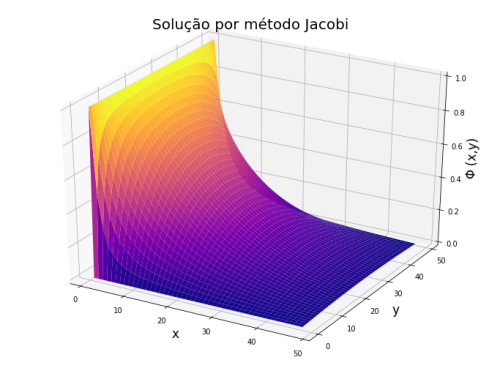
### Exemplo para o algoritmo de jacobi, Equação de Laplace ###
# P é a matriz do potencial no tempo n
# Q é a matriz do potencial no tempo n+1

while t < tmax: # Loop temporal
  
  for i in range(1,L+1):  # Loop em x
    for j in range(1,L+1): # Loop em y
      Q[i][j] = (P[i+1][j] + P[i-1][j] + P[i][j+1] + P[i][j-1])/4 
  
  P = Q.copy()
  t = t + td

plt.plot(x,y,P) # plotagem dos gráficos

Solução numérica do problema da borda carregada.

• 

  Erro relativo médio para a solução de Gauss-Seidel para várias iterações.

Link para Códigos

Fizemos no ambiente Colab em .ipynb, segue link do github:[1]