Difusão ambipolar em plasmas: mudanças entre as edições
Sem resumo de edição |
|||
| Linha 3: | Linha 3: | ||
Diferentemente de um gás de partículas neutras, um plasma (elétrons e íons), são menos livres ao se moverem por causa da atração coulombiana. Em um caso em que um plasma se movimenta elvolto em um gás neutro, os coeficientes de difusão dos elétrons e dos íons são tipicamente dados por | Diferentemente de um gás de partículas neutras, um plasma (elétrons e íons), são menos livres ao se moverem por causa da atração coulombiana. Em um caso em que um plasma se movimenta elvolto em um gás neutro, os coeficientes de difusão dos elétrons e dos íons são tipicamente dados por | ||
<math> D_e = \frac{k_bT_e}{m_e\nu_e} | <math> D_e = \frac{k_bT_e}{m_e\nu_e} </math> e <math> D_i = \frac{h_bT_i}{m_i\nu_i} </math> | ||
onde <math>T_e</math>, <math>T_i</math>, <math>m_e</math>, <math>m_i</math>, <math>\nu_e</math> e <math>\nu_i</math>, são as temperaturas, massas e frequências de colisão dos elétrons e íons com os isótopos dos átomos neutros. | onde <math>T_e</math>, <math>T_i</math>, <math>m_e</math>, <math>m_i</math>, <math>\nu_e</math> e <math>\nu_i</math>, são as temperaturas, massas e frequências de colisão dos elétrons e íons com os isótopos dos átomos neutros. | ||
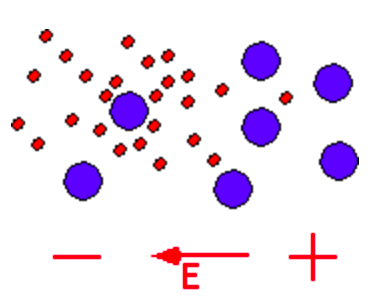
Devido à massa do elétron ser muito menor que a massa de um íon, <math>D_e</math> é maior que <math>D_i</math>, então quando um plasma começa a se espalhar, incialmente os elétrons se espalham mais rapidamente que os íons e isso gera um campo elétrico que freia os elétron e acelera os íons. | Devido à massa do elétron ser muito menor que a massa de um íon, <math>D_e</math> é maior que <math>D_i</math>, então quando um plasma começa a se espalhar, incialmente os elétrons se espalham mais rapidamente que os íons e isso gera um campo elétrico que freia os elétron e acelera os íons. | ||
(botar uma figura aqui) | (botar uma figura aqui)[[Arquivo: diff.png]] | ||
Como mostrado por Shimony e Cahn<ref name=Simony+Cahn64> Z. Shimony and J. H. Cahn, "Time-dependent ambipolar diffusion waves", The Physics of Fluids 8, 1704 (1965) </ref>, esse problema é descrito por uma equação de onda amortecida: | |||
<math> \ | <math>\nabla^2 n(\vec r,t) = \frac{1}{u^2} \frac{\partial^2 n(\vec r,t)}{\partial t^2} + \alpha \frac{\partial n(\vec r,t)}{\partial t} \qquad (1)</math> | ||
<math> | onde <math>u^2 = \nu_a D_a</math> e <math>\alpha = 1/D_a</math>, sendo \nu_a a frequência de colisão ambipolar e D_a o coeficiente de difusão ambipolar, que pode ser escrito como <math>D_a = D_i(1+T_e/T_i)</math> <ref name=Da> http://uigelz.eecs.umich.edu/classes/pub/eecs517/handouts/derivation_ambipolar_diffusion_v02.pdf </ref>. | ||
== O Método == | == O Método == | ||
== Resultados e Discussão== | == Resultados e Discussão== | ||
| Linha 41: | Linha 26: | ||
== Referências == | == Referências == | ||
<references/> | |||
Edição das 14h27min de 31 de março de 2021
Equação da difusão ambipolar
Diferentemente de um gás de partículas neutras, um plasma (elétrons e íons), são menos livres ao se moverem por causa da atração coulombiana. Em um caso em que um plasma se movimenta elvolto em um gás neutro, os coeficientes de difusão dos elétrons e dos íons são tipicamente dados por
e
onde , , , , e , são as temperaturas, massas e frequências de colisão dos elétrons e íons com os isótopos dos átomos neutros. Devido à massa do elétron ser muito menor que a massa de um íon, é maior que , então quando um plasma começa a se espalhar, incialmente os elétrons se espalham mais rapidamente que os íons e isso gera um campo elétrico que freia os elétron e acelera os íons.
Como mostrado por Shimony e Cahn[1], esse problema é descrito por uma equação de onda amortecida:
onde e , sendo \nu_a a frequência de colisão ambipolar e D_a o coeficiente de difusão ambipolar, que pode ser escrito como [2].
O Método
Resultados e Discussão
Programas Utilizados
Referências
- ↑ Z. Shimony and J. H. Cahn, "Time-dependent ambipolar diffusion waves", The Physics of Fluids 8, 1704 (1965)
- ↑ http://uigelz.eecs.umich.edu/classes/pub/eecs517/handouts/derivation_ambipolar_diffusion_v02.pdf