Grupo - Dilema Do Prisioneiro: mudanças entre as edições
| (10 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 16: | Linha 16: | ||
- duas ações possíveis | - duas ações possíveis | ||
Nesta Wiki será utilizado | Nesta Wiki será utilizado a versão mais comum nas literaturas, onde o dilema do prisioneiro é interpretado de forma diferente: | ||
Ambos os presos são apresentados com a possibilidade de cooperar(assumir o crime que ele e seu comparsa cometeram) ou Não assumir o crime. | Ambos os presos são apresentados com a possibilidade de cooperar(assumir o crime que ele e seu comparsa cometeram) ou Não assumir o crime. | ||
| Linha 37: | Linha 37: | ||
Neste esquema de jogo, o melhor a se fazer para beneficio mútuo seria cooperar, para que nenhum dos dois passe 10 anos na cadeia. Porém, não há como saber como o outro jogador irá responder ao jogo, Pois se você cooperar e seu comparsa negar o crime, você passará 10 anos na prisão e ele sai livre. | Neste esquema de jogo, o melhor a se fazer para beneficio mútuo seria cooperar, para que nenhum dos dois passe 10 anos na cadeia. Porém, não há como saber como o outro jogador irá responder ao jogo, Pois se você cooperar e seu comparsa negar o crime, você passará 10 anos na prisão e ele sai livre. | ||
Este problema é chamado também de jogo de soma não zero, onde não é possível unilateralmente mudar o resultado do jogo. | Este problema é chamado também de jogo de soma não zero, onde não é possível unilateralmente mudar o resultado do jogo. | ||
===Dilema ''SnowDrift''=== | ===Dilema ''SnowDrift''=== | ||
| Linha 133: | Linha 132: | ||
===Dilema do prisioneiro=== | ===Dilema do prisioneiro=== | ||
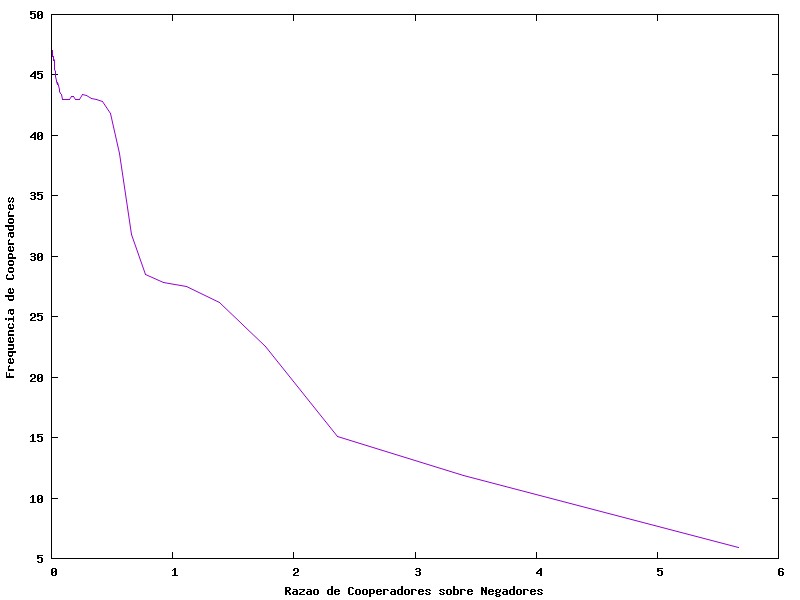
[[Arquivo:FreqXRazão.jpg |frame|400x400px|center|Frequência Cooperadores X razão Custo/Beneficio - r = | Analizando as diferentes possibilidades de razões custo/benefício obtemos o gráfico abaixo. | ||
[[Arquivo:FreqXRazão.jpg |frame|400x400px|center|Frequência Cooperadores X razão Custo/Beneficio - r = c/(b-c)]] | |||
Nele podemos verificar que quando o custo de cooperar chega a zero, hávará um equilíbrio de 40% de cooperadores e 60% de negadores. e quando a razão custo/beneficio começa a aumentar(aumento do custo) a porcentagem de cooperadores começa a declinar rapidamente e logo chega a zero. | |||
Logo em seguida, temos os gráficos de partes específicas dos resultados obtidos no gráfico anterior. nele vemos que com custo = 1, beneficio = 2, os cooperadores são eliminados rapidamente. | |||
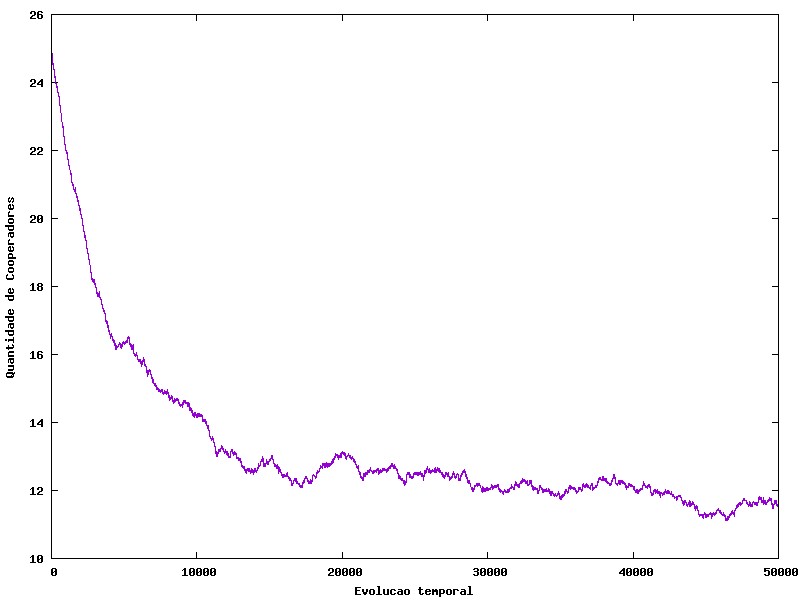
[[Arquivo:CF01.jpg |frame|400x400px|center|B = 2 c = 1.0]] | [[Arquivo:CF01.jpg |frame|400x400px|center|B = 2 c = 1.0]] | ||
A seguir temos uma imagem que mostraremos como auxílio visual representando o momento inicial do gráfico anterior e o momento final dele, onde em preto temos os negadores, e em branco os cooperadores. | |||
<gallery widths=400px heights=400px> | <gallery widths=400px heights=400px> | ||
Arquivo:IM_1.jpg|B = 2 c = 1.0 | Arquivo:IM_1.jpg|B = 2 c = 1.0 | ||
| Linha 146: | Linha 149: | ||
Agora temos um exemplo no qual o benefício =2 e o custo = 0.01 geram um caso no qual há a possibilidade de equilibro após certo tempo. | |||
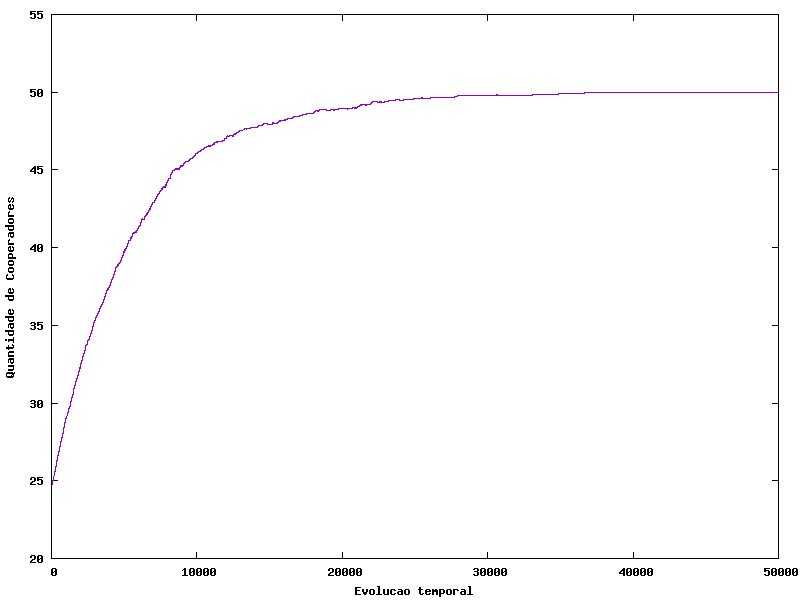
[[Arquivo:CF0.01.jpg |frame|400x400px|center|B = 2 c = 0.01]] | [[Arquivo:CF0.01.jpg |frame|400x400px|center|B = 2 c = 0.01]] | ||
| Linha 157: | Linha 160: | ||
</gallery> | </gallery> | ||
Aqui veremos que com custo de 0.01 o equilibrio gira em torno de 45% de cooperadores para 65% de negadores, e é importante observar que os cooperadores de aglutinam com o decorrer do tempo, formando colônias dentro da população onde todos cooperam. | |||
[[Arquivo:CF0.0001.jpg |frame|400x400px|center|B = 2 c = 0. | Agora temos o caso onde o custo é muito baixo e os cooperadores chegam ao equilíbrio de mais ou menos 65% de cooperadores para 35% de negadores. | ||
[[Arquivo:CF0.0001.jpg |frame|400x400px|center|B = 2 c = 0.0001]] | |||
<gallery widths=400px heights=400px> | <gallery widths=400px heights=400px> | ||
| Linha 168: | Linha 173: | ||
===Dilema ''SnowDrift''=== | ===Dilema ''SnowDrift''=== | ||
Neste problema analizamos duas situações diferentes, onte fixamos b = 2 e variamos c entre 1.5 e 0.00010, abaixo temos a frequência de cooperadores quando se muda o valor de c através da relação de busto benefício. | |||
[[Arquivo:SD_FreqXRazão.jpg |frame|400x400px|center|Frequência Cooperadores X razão Custo/Beneficio - r = c/(b-c]] | |||
Agora temos o gráfico da quantidade de cooperadores pela evolução temporal quando o custo = 1.5. | |||
[[Arquivo:SD_CF1.5.jpg |frame|400x400px|center|B = 2 c = 1.5]] | |||
<gallery widths=400px heights=400px> | |||
Arquivo:SD_IM_1.5.jpg|B = 2 c = 1.5 | |||
Arquivo:SD_FM1.5.jpg|B = 2 c = 1.5 | |||
</gallery> | |||
Vemos que com o custo alto, os cooperadores são quase extintos predominando os negadores. Porém, quando temos o custo bem baixo, os negadores praticamente somem, como podemos ver os gráficos abaixo. | |||
[[Arquivo:SD_CF0.0001.jpg |frame|400x400px|center|B = 2 c = 0.0001]] | |||
<gallery widths=400px heights=400px> | |||
Arquivo:SD_IM_0.0001.jpg |B = 2 c = 0.0001 | |||
Arquivo:SD_FM_0.0001.jpg |B = 2 c = 0.0001 | |||
</gallery> | |||
==Implementação em C== | ==Implementação em C== | ||
Edição atual tal como às 03h43min de 25 de janeiro de 2018
Integrantes do grupo: Leonardo Xavier Rodrigues (262696) e Rodrigo Lopes de Sousa Silva (262705)
Introdução
O dilema do prisioneiro junto com o dilema SnowDrift são problemas pertencentes a teoria dos jogos. Ambos funcionam de formas similares, baseando-se na interação entre duas pessoas(ou jogadores) e nas suas possíveis escolhas estratégicas para resolver seu problema. Esses dilemas são muito usados como metáforas para tentar explicar a evolução da cooperação através da seleção natural. O dilema do prisioneiro também poder ser usado para interpretar diversas outras formas de interação, desde biológicas até questões de economia.
Dilema Do Prisioneiro
O dilema do prisioneiro clássico é descrito como uma mini história:
Dois suspeitos, A e B, são presos pela polícia. A polícia tem provas insuficientes para os condenar, mas, separando os prisioneiros, oferece a ambos o mesmo acordo: se um dos prisioneiros, confessando, testemunhar contra o outro e esse outro permanecer em silêncio, o que confessou sai livre enquanto o cúmplice silencioso cumpre 10 anos de sentença. Se ambos ficarem em silêncio, a polícia só pode condená-los a 6 meses de cadeia cada um. Se ambos traírem o comparsa, cada um leva 5 anos de cadeia. Cada prisioneiro faz a sua decisão sem saber que decisão o outro vai tomar, e nenhum tem certeza da decisão do outro. A questão que o dilema propõe é: o que vai acontecer? Como o prisioneiro vai reagir? Ref
Existem diversas versões deste dilema, variando os anos de prisão, mas todas com a mesma estrutura simples:
- dois jogadores
- duas ações possíveis
Nesta Wiki será utilizado a versão mais comum nas literaturas, onde o dilema do prisioneiro é interpretado de forma diferente:
Ambos os presos são apresentados com a possibilidade de cooperar(assumir o crime que ele e seu comparsa cometeram) ou Não assumir o crime. esse esquema pode ser visto visualmente com o auxilio de uma matriz chamada de matriz de ganhos
| A, B | Coopera | Nega |
|---|---|---|
| Nega | Ganho,Perda | Perda, Perda |
| Coopera | Ganho Menor, Ganho Menor | Perda, Ganho |
Onde ganho seria receber a liberdade imediata, perda a prisão por 10 anos e ganho menor a prisão por 5 anos. Neste esquema de jogo, o melhor a se fazer para beneficio mútuo seria cooperar, para que nenhum dos dois passe 10 anos na cadeia. Porém, não há como saber como o outro jogador irá responder ao jogo, Pois se você cooperar e seu comparsa negar o crime, você passará 10 anos na prisão e ele sai livre. Este problema é chamado também de jogo de soma não zero, onde não é possível unilateralmente mudar o resultado do jogo.
Dilema SnowDrift
Este dilema utiliza quase a mesma estrutura do anterior, porém com apenas alguns detalhes de diferença.
Nesta metáfora, duas pessoas estão em um carro preso em uma nevasca, cada uma delas tem a opção de sair do carro e com uma pá cavar a neve ao redor do carro ou simplesmente não fazer nada. nesta situação, diferentemente do dilema anterior, a melhor opção a se tomar quando o outro jogador se nega a colaborar ainda é colaborar, caso contrário você continuará preso na neve.
Tipos de população
As metáforas apresentadas acima são usadas para tentar explicar o aparecimento natural da cooperação através da seleção natural. Foram utilizados dois tipos de modelo de populações neste estudo.
O jogo é feito através da interação de um jogador com outro jogador, dependendo do algoritmo utilizado.
População misturada
Neste cenário a ideia é reproduzir um modelo de uma população na qual o jogador pode interagir com qualquer outro membro da população, um exemplo desse tipo de estrutura seria uma colonia de bactérias vivendo em um meio líquido, no qual elas podem se mover.
População Estruturada
Neste cenário o modelo simulado seria um no qual um membro da população pode apenas interagir com seus vizinhos próximos, na biologia uma placa de Petri(dish) com colonias de bactérias na superfície seria um bom exemplo desse modelo, já que nele as bactérias não podem se locomover.
Conceitos do jogo
Para implementar os dilemas em uma simulação e estudar seus resultados será analisado a matrix de ganhos para um jogador (p1) contra um segundo jogador (p2).
| P1, P2 | Nega | Coopera |
|---|---|---|
| Nega | P | T |
| Coopera | S | R |
P - Punishment
T - Temptation
S - Sucker's Payoff
R - Reward
Quando ambos Cooperam, o player um recebe a recompensa(Reward ), se ambos negam, o jogador 1 recebe punição(Punishment). Se o jogador um nega e o jogador 2 coopera, o primeiro receberá a tentação(Temptation), Caso contrário, o jogador um recebe Sucker's Payoff.
Algoritmos
Os jogos são feitos para estudar o comportamento de uma população e a sobrevivência da cooperação nela, para este fim é necessário dar valores a matriz de ganhos. Cada jogo é feito de diversas rodadas onde há a interação da população assincronamente. Para cooperar existe um beneficio(b) e um custo(c), e a matriz de ganhos é baseada nesses valores.
Características dilema do prisioneiro
R = b-c
T = b
S = -c
P = 0
O dilema do prisioneiro, geralmente, segue a regra T > R > P > S.
Características Para dilema SnowDrift
R = b-c/2
T = b
S = b-c
P = 0
Neste jogo há uma diferença crucial, na qual se ambos se negarem a ajudar, eles continuarão presos na neve.
O jogo
O jogo é feito de diversas maneiras, neste exemplo foram utilizadas dois tipos de estruturas de populações. O foco do jogo é descobrir se o jogador um irá ou não adotar a estratégia do jogador dois, para isso eles competem, porém competem indiretamente. Eles competem com seus vizinhos e o resultado disso(score) é utilizado para computar a probabilidade do jogador 1 assumir a estratégia feita pelo jogador 2.
População Misturada
Neste esquema de jogo, a população é aleatoriamente composta por cooperadores e negadores (50/50) e é escolhido aleatoriamente dois membros da população para competir, cada um deles joga contra algum outro membro aleatório da população. os seus respectivos scores são comparados e assim é feita a probabilidade do jogador um copiar a estratégia do jogador 2(w). , onde alpha será a diferença máxima entre os valores da matriz de ganho, para garantir que W seja menor que 1.
População Estruturada
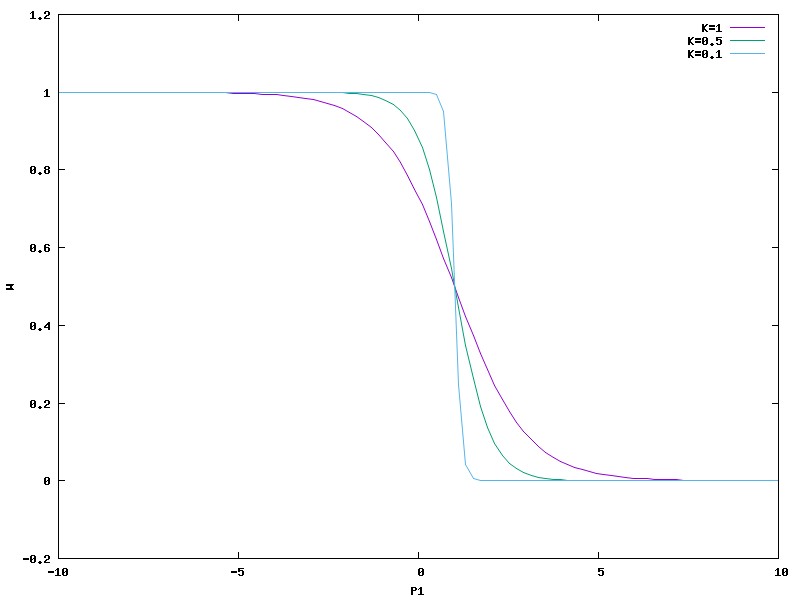
A população estruturada simula uma condição onde os membros não tem como interagir com qualquer outro membro da população, para isso é feito uma matriz n x n com a população de tamanho n. em cada rodada do jogo é escolhido algum membro aleatório da população nessa matriz e ele ira interagir com seus 4 mais próximos vizinhos, para comparar, sera utilizado um desses vizinhos e ele também irá competir com seus 4 vizinhos mais próximos. com base nesse score acumulado das 4 interações é calculado a probabilidade do jogador 1 assumir a estratégia do seu competidor. A formulá utilizada foi a de fermi dirac:
Com essa fórmula é introduzida uma certa aleatoriedade na decisão do jogador 1, pois mesmo que seu score seja maior, há a chance dele adotar a estratégia de seu oponente. isto pode ser interpretado como uma mutação, dependendo da análise feita.
Resultados
Dilema do prisioneiro
Analizando as diferentes possibilidades de razões custo/benefício obtemos o gráfico abaixo.
Nele podemos verificar que quando o custo de cooperar chega a zero, hávará um equilíbrio de 40% de cooperadores e 60% de negadores. e quando a razão custo/beneficio começa a aumentar(aumento do custo) a porcentagem de cooperadores começa a declinar rapidamente e logo chega a zero.
Logo em seguida, temos os gráficos de partes específicas dos resultados obtidos no gráfico anterior. nele vemos que com custo = 1, beneficio = 2, os cooperadores são eliminados rapidamente.
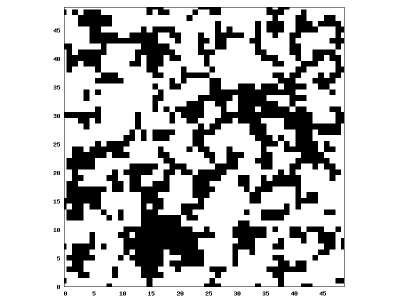
A seguir temos uma imagem que mostraremos como auxílio visual representando o momento inicial do gráfico anterior e o momento final dele, onde em preto temos os negadores, e em branco os cooperadores.
Agora temos um exemplo no qual o benefício =2 e o custo = 0.01 geram um caso no qual há a possibilidade de equilibro após certo tempo.
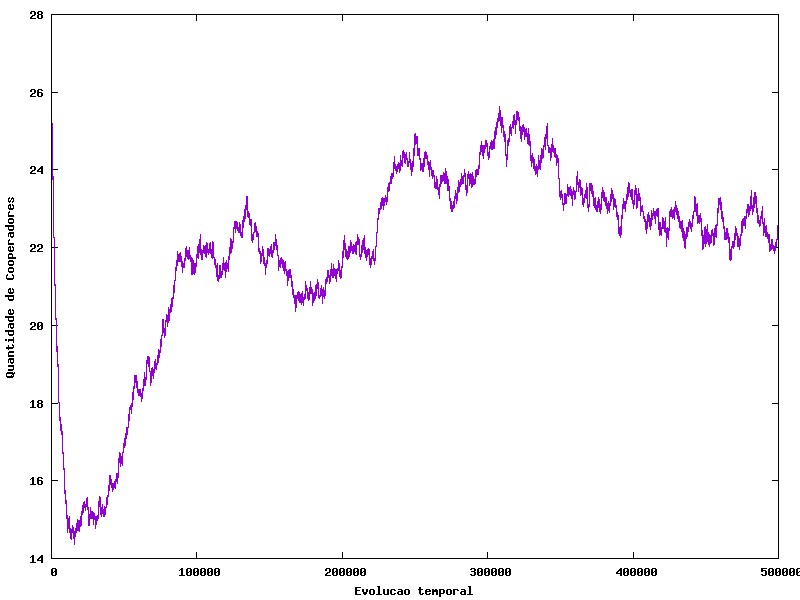
Aqui veremos que com custo de 0.01 o equilibrio gira em torno de 45% de cooperadores para 65% de negadores, e é importante observar que os cooperadores de aglutinam com o decorrer do tempo, formando colônias dentro da população onde todos cooperam.
Agora temos o caso onde o custo é muito baixo e os cooperadores chegam ao equilíbrio de mais ou menos 65% de cooperadores para 35% de negadores.
Dilema SnowDrift
Neste problema analizamos duas situações diferentes, onte fixamos b = 2 e variamos c entre 1.5 e 0.00010, abaixo temos a frequência de cooperadores quando se muda o valor de c através da relação de busto benefício.
Agora temos o gráfico da quantidade de cooperadores pela evolução temporal quando o custo = 1.5.
Vemos que com o custo alto, os cooperadores são quase extintos predominando os negadores. Porém, quando temos o custo bem baixo, os negadores praticamente somem, como podemos ver os gráficos abaixo.
Implementação em C
Link para Programas Usados[[1]]
Bibliografia
- Dusan Misevic,Sebastian Bonhoeffer, Spatial cooperation games
- Game theory and physics, American Journal of Physics 73, 405 (2005)
http://dx.doi.org/10.1119/1.1848514
- MARTIN A. NOWAK, SEBASTIAN BONHOEFFER, AND ROBERT M. MAY,Spatial games and the maintenance of cooperation
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC43892/pdf/pnas01133-0277.pdf
- Behavioural evolution: Cooperate with thy neighbour?
https://www.nature.com/articles/428611a
- Human cooperation in social dilemmas: comparing the Snowdrift game with the Prisoner's Dilemma
http://dx.doi.org/10.1098/rspb.2007.0793
- Delação premiada e Teoria dos Jogos | Nerdologia 271