Grupo2 - Ondas1: mudanças entre as edições
(→Código) |
|||
| (142 revisões intermediárias por 4 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
'''Integrantes do grupo:''' Rodrigo Zamin Ferreira (262692), Leonardo Xavier Rodrigues (262696), Maurício Gomes de Queiroz (264889) e Rodrigo Lopes de Sousa Silva (262705) | |||
==Introdução== | ==Introdução== | ||
| Linha 4: | Linha 7: | ||
Aqui será apresentado um modelo baseado em uma condição inicial e um perfil topográfico do local estudado que descreve a evolução temporal de uma onda. | Aqui será apresentado um modelo baseado em uma condição inicial e um perfil topográfico do local estudado que descreve a evolução temporal de uma onda. | ||
Inicialmente, para testarmos os diferentes métodos, utilizaremos a equação da onda em uma dimensão, que é uma equação diferencial parcial de segunda ordem, para modelarmos uma corda: | |||
<math> \frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^{2} u}{\partial x^{2}} </math> | |||
em que <math> u(x, t) </math> é o deslocamento vertical da corda, <math>c</math> é a velocidade de propagação da onda e <math> 0<x<L </math>, com <math> L </math> o comprimento da corda. | |||
Podemos reescrever a equação da seguinte forma: | |||
<math> \frac{\partial}{\partial t} \Big( \frac{\partial u}{\partial t} \Big) = c\frac{\partial}{\partial x} \Big( c\frac{\partial u}{\partial x} \Big) </math> . | |||
<math> | Uma vez que os métodos citados abaixo são para equações de primeira ordem, é necessário separarmos a equação em um sistema de equações, fazendo a substituição <math> v=\frac{\partial u}{\partial t} </math> e <math> w= c\frac{\partial u}{\partial x} </math>, de forma que: | ||
<math> | |||
\begin{cases} | |||
\dfrac{\partial v}{\partial t}=c\dfrac{\partial w}{\partial x} \\ | |||
\\ | \\ | ||
\ | c\dfrac{\partial v}{\partial x}=\dfrac{\partial w}{\partial t} \\ | ||
\end{ | |||
\end{cases} | |||
</math> | |||
Aqui usaremos <math>c=1</math>, sem perda de generalidade. As condições de contorno utilizadas aqui são <math> u(0, t) = u(L, t) = 0 </math> (pontas fixas), e as condições iniciais são <math> u(x,0) = \sin{\Big(\frac{\pi x}{L}\Big)} </math> e <math> \frac{\partial u}{\partial t}(x, 0) = 0 </math> | |||
==Algoritmos== | ==Algoritmos== | ||
Apresentaremos aqui três abordagens diferentes para a solução da equação diferencial parcial apresentada, e após, seus respectivos erros associados. | Apresentaremos aqui três abordagens diferentes para a solução da equação diferencial parcial apresentada, e após, seus respectivos erros associados. A respeito das discretizações, <math> j </math> corresponde à posição, e <math> n </math> representa o tempo. | ||
===Método de Lax-Friedrichs === | |||
Esse método de ordem <math> \mathcal{O}(\Delta x^2, \Delta t)</math><ref name=recipes></ref> consiste em inicialmente discretizar as equações no esquema FTCS (Forward Time Centered Space), ou seja, discretizando a derivada temporal utilizando os tempos <math>n</math> e <math>n+1</math> e a derivada espacial através das posições <math>j-1</math> e <math>j+1</math>: | |||
<math> \frac{1}{\Delta t}(v_{j}^{n+1} - v_j^n) = \frac{1}{2\Delta x} (w_{j+1}^{n} - w_{j-1}^{n}) </math>, | |||
<math> \frac{1}{\Delta t}(w_{j}^{n+1} - w_j^n) = \frac{1}{2\Delta x} (v_{j+1}^{n} - v_{j-1}^{n})</math>. | |||
Resultando em | |||
<math> v_{j}^{n+1} = v_j^n + \frac{\Delta t}{2\Delta x}(w_{j+1}^{n} - w_{j-1}^{n}) </math>, | |||
<math> w_{j}^{n+1} = w_j^n + \frac{\Delta t}{2\Delta x}(v_{j+1}^{n} - v_{j-1}^{n}) </math>. | |||
Entretanto, ao se realizar uma análise de estabilidade de Von Neumann, conclui-se que esse método é instável<ref name=recipes>Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007). "Numerical Recipes: The Art of Scientific Computing" (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8.</ref> . Para torná-lo estável, é necessário trocarmos os termos <math> v_j^n </math> e <math> w_j^n </math> por suas médias espaciais, chegando, assim, na expressão do esquema de Lax-Friedrichs: | |||
<math> v_{j}^{n+1} = \Big( \frac{ v_{j-1}^{n} + v_{j+1}^{n}}{2} \Big) + \frac{\Delta t}{2\Delta x}(w_{j+1}^{n} - w_{j-1}^{n}) </math>, | |||
<math> w_{j}^{n+1} = \Big( \frac{ w_{j-1}^{n} + w_{j+1}^{n}}{2} \Big) + \frac{\Delta t}{2\Delta x}(v_{j+1}^{n} - v_{j-1}^{n}) </math>. | |||
Para obtermos o valor de <math> u_{j}^{n+1} </math>, que é o nosso objetivo, discretizamos a equação <math> \frac{\partial u}{\partial t} = v</math> | |||
<math> u_{j}^{n+1} = u_{j}^{n} + v_{j}^{n}\Delta t </math>, | |||
Embora as médias espaciais sejam necessárias para a estabilidade do método, elas introduzem um problema: surge um efeito chamado de dissipação numérica, ou seja, a amplitude da solução diminui com o tempo. Isso pode ser observado através da análise de Von Neumann ou de uma investigação da equação do esquema Lax-Friedrichs <ref name=recipes/> . Por este método, observa-se que ao inserirmos as médias, mudamos a equação original do problema, pois agora há também um termo do tipo difusivo (uma derivada segunda), com constante de difusão <math>\frac{(\Delta x)^2}{2\Delta t}</math> <ref name=recipes/>. | |||
Agora vamos unir todas as equações, utilizando, além da equação para <math>u</math> obtida acima, as discretizações de <math> v=\frac{\partial u}{\partial t} </math> e <math> w= \frac{\partial u}{\partial x} </math> | |||
<math> v_j^n = \frac{1}{\Delta t} (u_{j}^{n+1} - u_{j}^{n})</math>, | |||
<math> w_j^n = \frac{1}{2\Delta x} (u_{j+1}^{n} - u_{j-1}^{n})</math>. | |||
Assim, obtemos | |||
<math> u_{j}^{n+1} = u_{j}^{n} + \Big( \frac{u_{j-1}^{n} + u_{j+1}^{n}}{2} \Big) - \Big( \frac{u_{j-1}^{n-1} + u_{j+1}^{n-1}}{2} \Big) + \frac{(\Delta t)^2}{4(\Delta x)^2} \Big( u_{j-2}^{n-1} -2u_{j}^{n-1} + u_{j+2}^{n-1}\Big) </math>. | |||
===Método de Leapfrog === | |||
Neste método , de ordem <math> \mathcal{O}(\Delta x^2, \Delta t^2 )</math> <ref name=recipes></ref>, utilizamos os pontos intermediários na discretização das equações. | |||
Para <math>v</math> temos | |||
<math> \frac{1}{\Delta t}\bigg( v_{j}^{n+\frac{1}{2}} - v_{j}^{n-\frac{1}{2}}\bigg) = \frac{1}{\Delta x}\Big(w_{j+\frac{1}{2}}^{n} - w_{j-\frac{1}{2}}^{n}\bigg) \Rightarrow v_{j}^{n+\frac{1}{2}} = v_{j}^{n-\frac{1}{2}} + \frac{\Delta t}{\Delta x} \bigg(w_{j+\frac{1}{2}}^{n} - w_{j-\frac{1}{2}}^{n} \bigg) </math>, | |||
Para <math>w</math> temos | |||
<math> \frac{1}{\Delta x}\bigg(v_{j+1}^{n+\frac{1}{2}} - v_{j}^{n+\frac{1}{2}}\bigg) = \frac{1}{\Delta t}\bigg(w_{j+\frac{1}{2}}^{n+1} - w_{j+\frac{1}{2}}^{n} \bigg) \Rightarrow w_{j+\frac{1}{2}}^{n+1} = w_{j+\frac{1}{2}}^{n} + \frac{\Delta t}{\Delta x} \bigg(v_{j+1}^{n+\frac{1}{2}} - v_{j}^{n+\frac{1}{2}}\bigg) </math>, | |||
Para <math>u</math> temos | |||
<math> v_{j}^{n+\frac{1}{2}} = \frac{\partial u}{\partial t} \bigg|_{j}^{n+\frac{1}{2}} = \frac{1}{\Delta t} (u_{j}^{n+1} - u_j^n) \Rightarrow u_{j}^{n+1} = u_j^n + v_{j}^{n+\frac{1}{2}} \Delta t</math>, | |||
Utilizando o fato de que | |||
<math> v_{j}^{n+\frac{1}{2}} = \frac{1}{\Delta t} (u_{j}^{n+1} - u_j^n)</math>, | |||
<math>w_{j+\frac{1}{2}}^{n} = \frac{1}{\Delta x} (u_{j+1}^{n} - u_{j}^{n})</math>, | |||
chegamos na equação para <math>u_{j}^{n+1}</math> | |||
<math> u_{j}^{n+1} = 2u_{j}^{n} - u_{j}^{n-1} + \frac{(\Delta t)^2}{(\Delta x)^2}(u_{j+1}^{n} - 2u_{j}^{n} + u_{j-1}^{n}) </math>, | |||
o que é equivalente a discretizarmos a equação da onda diretamente, utilizando que, para uma função <math>f(x)</math>, | |||
<math> \frac{d^2f}{dx^2}\bigg|_j = \frac{1}{(\Delta x)^2}(f_{j-1} - 2f_j + f_{j+1})</math>, | |||
sendo <math>j</math> a discretização em <math>x</math>. | |||
===Método de Lax-Wendroff de Dois Passos === | |||
Para este método, de ordem <math> \mathcal{O}(\Delta x^2, \Delta t^2 )</math>, o primeiro passo consiste em calcular o valor de <math>v^{n+\frac{1}{2}}</math> e <math>w^{n+\frac{1}{2}}</math> utilizando o método de Lax-Friedrichs, para posterior cálculo de <math>v^{n+1}</math> e <math>w^{n+1}</math>: | |||
<math> v_{j+\frac{1}{2}}^{n+\frac{1}{2}} = \frac{1}{2}( v_{j+1}^{n} + v_{j}^{n} ) + \frac{\Delta t }{2\Delta x} (w_{j+1}^{n} - w_{j}^{n}) </math>, | |||
<math> v_{j-\frac{1}{2}}^{n+\frac{1}{2}} = \frac{1}{2}( v_{j}^{n} + v_{j-1}^{n} ) + \frac{\Delta t }{2\Delta x} (w_{j}^{n} - w_{j-1}^{n}) </math>, | |||
<math> w_{j+\frac{1}{2}}^{n+\frac{1}{2}} = \frac{1}{2}( w_{j+1}^{n} + w_{j}^{n} ) + \frac{\Delta t }{2\Delta x} (v_{j+1}^{n} - v_{j}^{n}) </math>, | |||
<math> w_{j-\frac{1}{2}}^{n+\frac{1}{2}} = \frac{1}{2}( w_{j}^{n} + w_{j-1}^{n} ) + \frac{\Delta t }{2\Delta x} (v_{j}^{n} - v_{j-1}^{n}) </math>, | |||
Agora, no tempo <math>n+1</math>: | |||
<math> w_{j}^{n+1} = \ | <math> v_{j}^{n+1} = v_{j}^{n} + \frac{\Delta t}{\Delta x} \bigg(w_{j+\frac{1}{2}}^{n+\frac{1}{2}} - w_{j-\frac{1}{2}}^{n+\frac{1}{2}}\bigg) </math>, | ||
<math> w_{j}^{n+1} = w_{j}^{n} + \frac{\Delta t}{\Delta x} \bigg(v_{j+\frac{1}{2}}^{n+\frac{1}{2}} - v_{j-\frac{1}{2}}^{n+\frac{1}{2}}\bigg) </math>, | |||
Agrupando as equações, | |||
<math> w_{j}^{n+1} = w_j^n + \frac{\Delta t}{\Delta x} \Bigg[\frac{1}{2}(v_{j+1}^{n} - v_{j-1}^{n}) + \frac{\Delta t}{2\Delta x} (w_{j+1}^{n} - 2 w_{j}^{n} + w_{j-1}^{n})\Bigg] </math>, | |||
<math> v_{j}^{n+1} = v_j^n + \frac{\Delta t}{\Delta x} \Bigg[\frac{1}{2}(w_{j+1}^{n} - w_{j-1}^{n}) + \frac{\Delta t}{2\Delta x} (v_{j+1}^{n} - 2 v_{j}^{n} + v_{j-1}^{n})\Bigg] </math>, | |||
E finalmente temos a equação unificada em u, utilizando a expressão para <math> v_{j}^{n+1} </math> e as discretizações de <math> v=\frac{\partial u}{\partial t} </math> e <math> w= \frac{\partial u}{\partial x} </math>, como obtidas na seção sobre o Método de Lax-Friedrichs: | |||
<math> u_{j}^{n+1} = u_{j}^{n} + v_{j}^{n}\Delta t </math> | <math> u_{j}^{n+1} = u_{j}^{n} + v_{j}^{n}\Delta t </math> | ||
<math> u_{j}^{n+1} = 2u_{j}^{n} - u_{j}^{n-1} + \frac{(\Delta t)^2}{2(\Delta x)^2}\Bigg[ \frac{1}{2}u_{j+2}^{n-1} - \frac{1}{2}u_{j-2}^{n-1} + u_{j+1}^{n} - u_{j+1}^{n-1} - 2u_{j}^{n} + u_{j}^{n-1} + u_{j-1}^{n} - u_{j-1}^{n-1}\Bigg] </math>, | |||
== Implementação== | |||
Ao implementarmos o método, surgem dois problemas: o problema não é auto-inicializável, pois para calcularmos o valor de <math>u_j^{1}</math>, necessitamos de <math>u_j^{-1}</math> (além de <math>u_j^{0}</math>). Entretanto, isto é rapidamente solucionado quando discretizamos a condição inicial de que <math> \frac{\partial u}{\partial t}(x, 0) = 0 </math>: | |||
<math>\frac{1}{2\Delta t} (u_j^{1} - u_j^{-1}) = 0 \Rightarrow u_j^{1} = u_j^{-1}</math>, | |||
<math> | ou seja, para o cálculo de <math>u_j^{-1}</math>, utilizamos que <math> u_j^{1} = u_j^{-1} </math>. Através do método de Leapfrog, dessa forma conseguimos isolar <math>u_j^{-1}</math>: | ||
<math> | <math> u_{j}^{-1} = 2u_{j}^{0} - u_{j}^{-1} + \frac{(\Delta t)^2}{(\Delta x)^2}(u_{j+1}^{0} - 2u_{j}^{0} + u_{j-1}^{0})</math>, | ||
<math> u_{j}^{-1} = u_{j}^{0} + \frac{(\Delta t)^2}{2(\Delta x)^2}(u_{j+1}^{0} - 2u_{j}^{0} + u_{j-1}^{0})</math>. | |||
<math> | Porém, isso não ocorre com os outros dois métodos, pois surgem termos em diferentes posições para o tempo <math>n=0</math> (de <math>u_{-2}^{0}</math>, <math>u_{-1}^{0}</math>, até <math>u_{2}^{0}</math>), sendo necessário resolvermos o sistema como um todo simultaneamente, ou seja, teríamos que inverter uma matriz. Por isso, foi utilizado o método de Leapfrog para o cálculo de <math>u_j^{-1}</math> em todos os métodos, devido a sua simplicidade. | ||
<math> | Além disso, são necessários valores de <math>u_{-1}^n</math> e de <math>u_{j_{max}+1}^n</math>, com <math>j_{max}</math> correspondendo a <math>x = L</math>, para calcularmos <math>u_1^{n}</math> e <math>u_{j_{max}}^{n}</math>, para qualquer tempo, utilizando os métodos de Lax-Wendroff de dois passos e Lax-Friedrichs. A solução a este problema foi utilizarmos | ||
<math>u_{-1}^n = -u_{1}^n </math> | |||
<math> | <math>u_{j_{max}+1}^n = -u_{j_{max}-1}^n </math>. | ||
<math> | Pensando na condição inicial <math> u(x,0) = \sin{\Big(\frac{\pi x}{L}\Big)} </math>, e estendendo para além da corda (pensando no seno de <math> -\infty<x<\infty </math>), observamos que ela respeita as equações acima. | ||
== Solução e Análise de erros == | |||
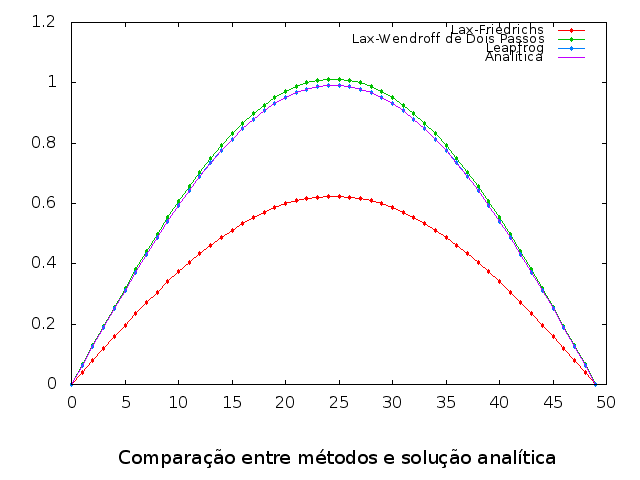
Primeiramente, apresentamos abaixo as soluções geradas pelos programas, em comparação com a solução analítica. | |||
[[Arquivo:Output_comp.png|frame|100px|center|Comparação da solução analítica com as soluções numéricas]] | |||
Aqui já podemos observar o que foi comentado na seção sobre o método de Lax-Friedrichs: devido à dissipação numérica inerente ao método, há uma diminuição da amplitude da onda ao longo do tempo, embora ela mantenha sua forma. Isso interferirá na análise do erro deste método, o que será apresentado na sequência. | |||
A partir do cálulo da solução analítica da equação da onda, podemos calcular quanto o valor obtido pelos métodos difere da solução real, o que leva a uma visualização do erro corrente em cada método de integração. | |||
Nesse caso, a solução é <math>u(x, t) = \cos{\Big(\frac{\pi t}{L}\Big)}\sin{\Big(\frac{\pi x}{L}\Big)}</math> <ref> | |||
Weisstein, Eric W. "Wave Equation--1-Dimensional." From MathWorld--A Wolfram Web Resource; disponível em: [http://mathworld.wolfram.com/WaveEquation1-Dimensional.html]; último acesso em 26/11/2017</ref>.A análise de erros se torna mais evidente durante a escolha do parâmetro <math>k</math>, onde <math>k = \frac{\Delta t}{\Delta x}</math>. Valores grandes trazem pouca acurácia, e valores pequenos necessitam de muito poder de computação (tempo e dinheiro). | |||
<math> | O erro foi obtido efetuando uma média espacial, ou seja, o programa foi evoluindo até um tempo final <math>t_f = 100</math>, e, em <math>t=t_f</math>, foi feita uma média sobre o valor absoluto da diferença entre a solução analítica e a numérica. Aqui variamos o valor de <math>\Delta t</math>, fixando <math> \Delta x=1</math>, de forma que <math>k=\Delta t</math>. | ||
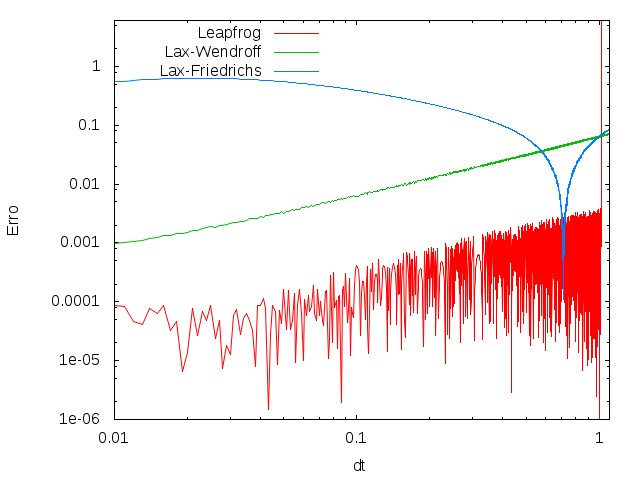
[[Arquivo:erro_dt.jpeg|frame|400px|center|Comparação do erro global entre os três métodos estudados com escala logarítimica em ambos os eixos]] | |||
Podemos observar que os erros crescem à medida que o parâmetro k se torna maior, como seria de se esperar. | |||
Além disso, sabendo a ordem do erro dos métodos, podemos determinar a inclinação da reta que melhor se ajusta aos pontos. Se um método tem erro de ordem <math>(\Delta t)^n</math>, | |||
<math>\varepsilon _l = \alpha (\Delta t)^n</math> | |||
em que <math>\varepsilon _l</math> é o erro local, ou seja, o erro de um passo do método, e <math>\alpha</math> é uma constante. Assim, o erro global <math>\varepsilon _g</math>, ou seja, o erro após N passos, é dado por | |||
<math>\varepsilon _g = N\varepsilon _l= N\alpha (\Delta t)^n </math> | |||
Como <math>N = \frac{t_f}{\Delta t}</math>, <math>\varepsilon _g = \frac{t_f}{\Delta t}\alpha (\Delta t)^n = \alpha t_f (\Delta t)^{n-1}</math>. | |||
Logo, se o erro local é de ordem <math>(\Delta t)^n</math>, o erro global (que é o que calculamos aqui) é de ordem <math>(\Delta t)^{n-1}</math>. Além disso, como utilizamos escala logarítmica para representar os resultados, a função do erro global se torna | |||
<math>\log{\varepsilon _g} = \log{\alpha t_f (\Delta t)^{n-1}} = \log{\alpha t_f} + (n-1)\log{(\Delta t)}</math> | |||
Ou seja, a inclinação do gráfico do erro global é <math>n-1</math>. | |||
Observamos que se determinarmos a reta que melhor se ajusta às curvas dos métodos de Leapfrog e Lax-Wendroff, ela tem inclinação aproximada de 1, já que os métodos são de ordem <math>(\Delta t)^2</math>. Com relação ao gráfico do erro do método de Lax-Friedrichs, é mais complicado de fazer sua análise, uma vez que há o efeito de dissipação numérica, que se intensifica para valores menores de <math>\Delta t</math>. Podemos observar nos dados que o ponto de máximo na parte esquerda do gráfico corresponde a um erro de aproximadamente <math>0,63</math>, que é a média da solução analítica no tempo <math>t = t_f</math> (conforme solução analítica, a amplitude no tempo <math>t=100</math> é <math>\cos{\Big(\frac{100\pi}{49}\Big)} \approx 1</math>, e a média de <math>\sin{\Big(\frac{\pi x}{L}\Big)}</math> vale <math>\frac{2}{\pi} \approx 0.64</math>). Isso significa que, devido à dissipação, a solução numérica é praticamente 0 frente à solução analítica na parte esquerda do gráfico. | |||
== Simulação de Propagação de Onda 2D Dependente de Topografia == | == Simulação de Propagação de Onda 2D no Mar Dependente de Topografia == | ||
O modelo mais simples parte da equação da onda [ | O modelo mais simples para a propagação de onda dependente da topografia parte da equação da onda <ref>Lie, Knut-Andreas. "The Wave Equation in 1D and 2D". Dept. of Informatics, University of Oslo; disponível em: [http://www.uio.no/studier/emner/matnat/ifi/INF2340/v05/foiler/sim04.pdf]; último acesso em 23/10/2017.</ref> <ref>Hjorth-Jensen, Morten. Computational Physics, University of Oslo, 2009.</ref>, incluindo uma velocidade dependente da posição, da forma <math>gH(x,y,t)</math>. | ||
<math> \frac{\partial^2 u}{\partial t^2} = \Big( \frac{\partial}{\partial x} | <math> \frac{\partial^2 u}{\partial t^2} = \Big( \frac{\partial}{\partial x} gH(x,y,t) \frac{\partial u}{\partial x}\Big) + \Big( \frac{\partial}{\partial y} gH(x,y,t) \frac{\partial u}{\partial y}\Big) - \frac{\partial^2 H}{\partial t^2} </math> , | ||
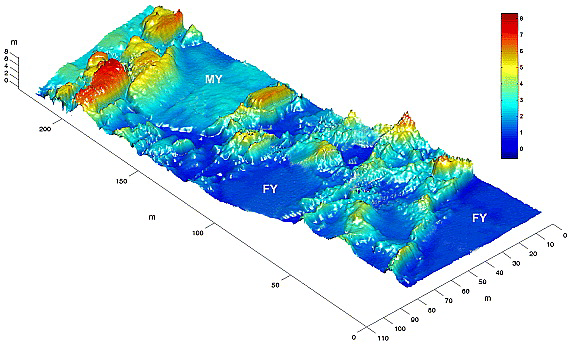
Sendo <math>H(x,y,t)</math> uma representação da profundidade em águas calmas. Em uma situação real, pode-se obtê-la por mapeamento eletrônico do terreno por sistema de sonar. | Sendo <math>H(x,y,t)</math> uma representação da profundidade em águas calmas, <math>g</math> a aceleração da gravidade e <math>u(x, y, t)</math> a elevação da água em relação ao nível de águas calmas. Em uma situação real, pode-se obtê-la por mapeamento eletrônico do terreno por sistema de sonar. A dependência em <math>t</math> de <math>H(x,y,t)</math> permite um modelo no qual o terreno se modifica com o tempo. Isto é, pode-se observar o efeito que o deslocamento de placas tectônicas, deslizamentos, e até explosões provocam no comportamento das ondas na costa de um país e o reconhecimento de áreas críticas. Entretanto, utilizaremos aqui <math>H = H(x, y)</math>, sem dependência no tempo, e mudaremos as condições iniciais para a modelagem do problema, além de usarmos <math>g=1</math>, para simplificarmos as expressões. | ||
[[Arquivo:Grupo2_ondas1_imagem1.png |500px|center| Exemplo de mapeamento de terreno sub - calota polar feito por AUV (''autonomous underwater vehicle'')]] | [[Arquivo:Grupo2_ondas1_imagem1.png |frame|500px|center| Exemplo de mapeamento de terreno sub - calota polar feito por AUV (''autonomous underwater vehicle'')<ref>Wadhams, M. J. Doble. "Digital terrain mapping of the underside of sea ice from a small AUV"; disponível em: DOI: 10.1029/2007GL031921 ; último acesso em 23/10/2017.</ref> ]] | ||
Como primeira abordagem visando uma análise em 2D, a integração da equação em 1D (mesmo sendo uma situação muito idealizada) já traz resultados interessantes. | Como primeira abordagem visando uma análise em 2D, a integração da equação em 1D (mesmo sendo uma situação muito idealizada) já traz resultados interessantes. Pode ser mostrado que a velocidade da onda pode ser dada por <math>v=\sqrt{gH}</math>, para o caso em que <math>\lambda<<H</math>, o que é razoável para um tsunami, que tem um comprimento de onda da ordem de até centenas de quilômetros, com uma profundidade da ordem de quilômetros<ref name=lang>Silveira, F. L.; Varriale, M. C. "Propagação das ondas marítimas e dos tsunami". Caderno Brasileiro de Ensino de Física, V. 22, N. 2: P. 190-215, 2005.</ref>. Como o período da onde não se altera <ref name=lang></ref>, quanto menor a profundidade, menor a velocidade, e menor o seu comprimento de onda. Além disso, devido à conservação de energia, e supondo que a extensão da frente de onda não seja alterada, é obtida a chamada Lei de Green<ref name=lang></ref>: | ||
[[Arquivo: | <math>\frac{A_2}{A_1} = \Bigg(\frac{H_1}{H_2}\Bigg)^{\frac{1}{4}}</math> | ||
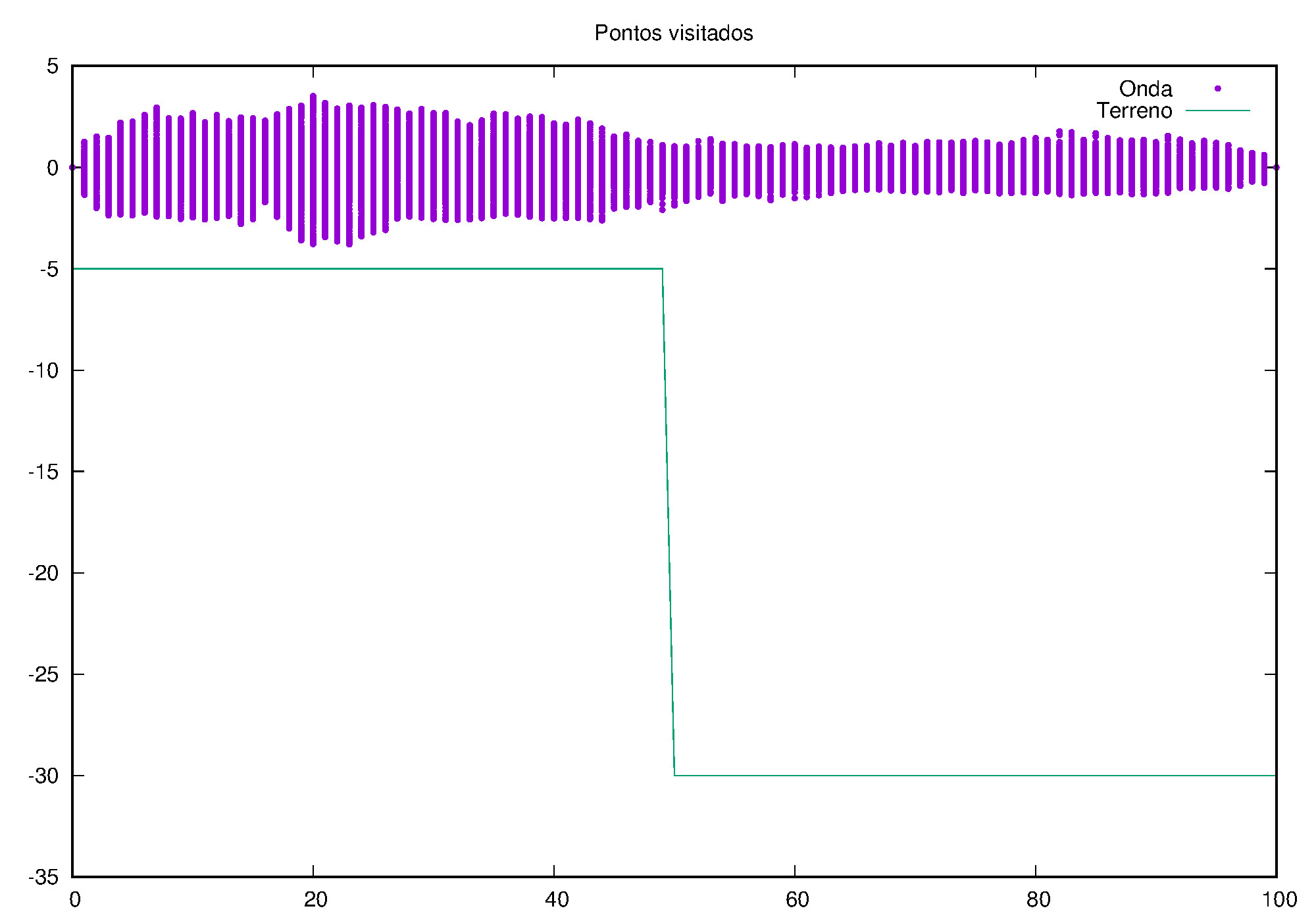
em que <math>A</math> é a amplitude da onda, e os índices representando dois meios. Logo, quanto menos profundo, maior a amplitude da onda. Esta informação por si só ajuda na construção de proteção contra quebra de ondas, pois é obtido o tamanho que as mesmas atingem. Nos gráficos abaixo podemos observar esses efeitos. | |||
[[Arquivo:top_visitados.jpg |frame|500x500px||center| Pontos visitados por simulação em 1D ]] | |||
E no caso em que simulamos uma fina camada de líquido, podemos ver a diminuição de velocidade da onda e o aumento de sua amplitude, especialmente no trecho mais à esquerda: | |||
[[Arquivo:camada_de_liquido.gif |frame|500px|center| Simulação em 1D de ondas perto da margem, com camada fina de líquido ]] | |||
É importante notar o quão poderosa é a integração de equações parciais na vida de um engenheiro. | É importante notar o quão poderosa é a integração de equações parciais na vida de um engenheiro. | ||
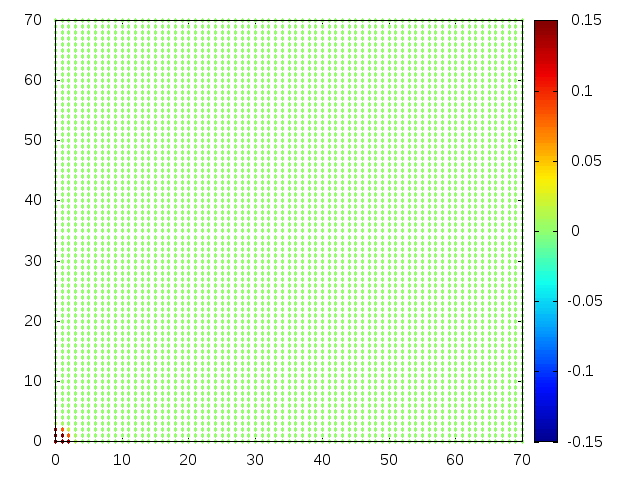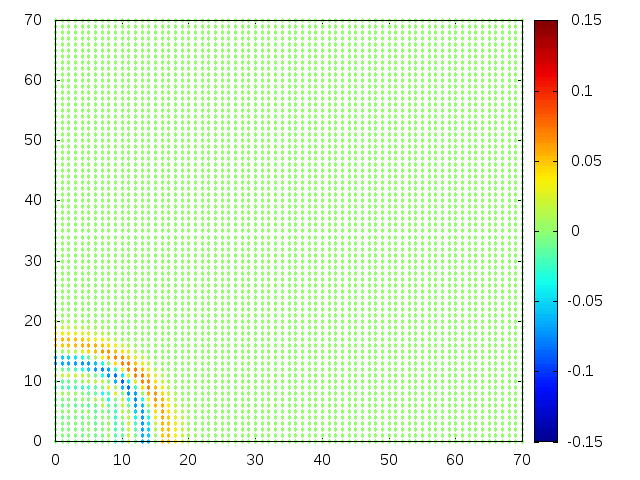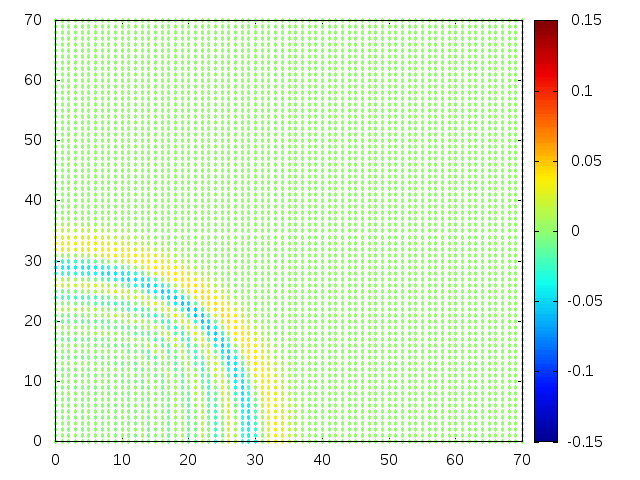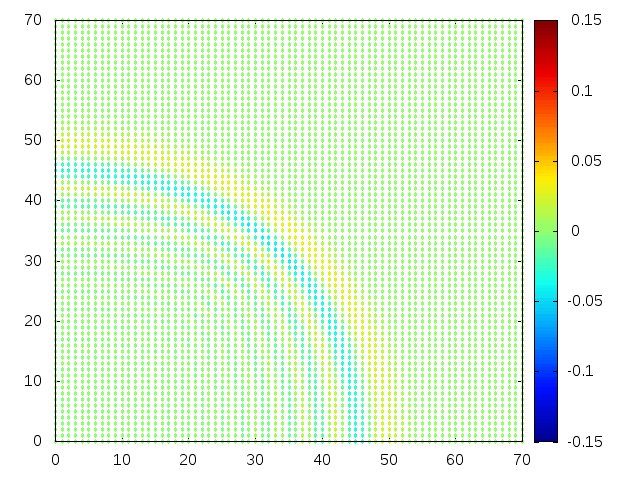
Estendendo o algoritmo de Leapfrog à situação 2D, obtemos, para uma condição inicial de uma gaussiana com média 0 e desvio padrão 1, tanto em <math>x</math> quanto em <math>y</math>, e <math>H(x,y) = 1</math>: | |||
[[Arquivo:02ss.gif |frame|500px|center|Simulação em 2D de ondas em águas com profundidade constante, visão de cima]] | |||
[[Arquivo:01ss.gif|frame|500px|center|Simulação em 2D de onda em águas com profundidade constante, visão em ângulo]] | |||
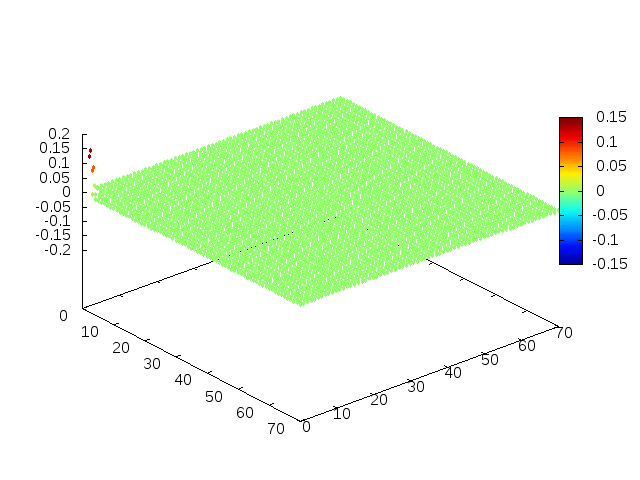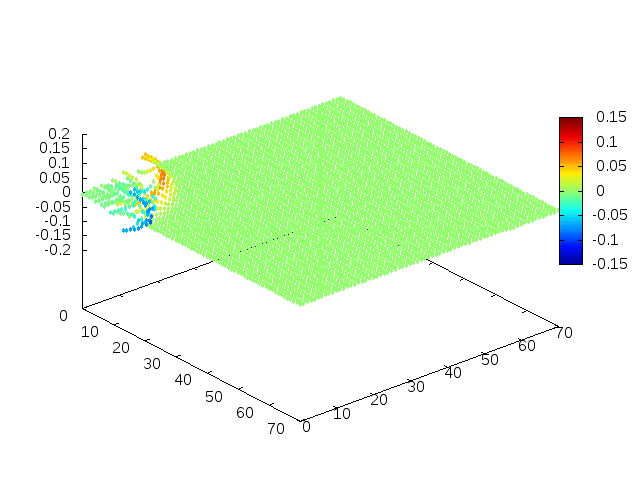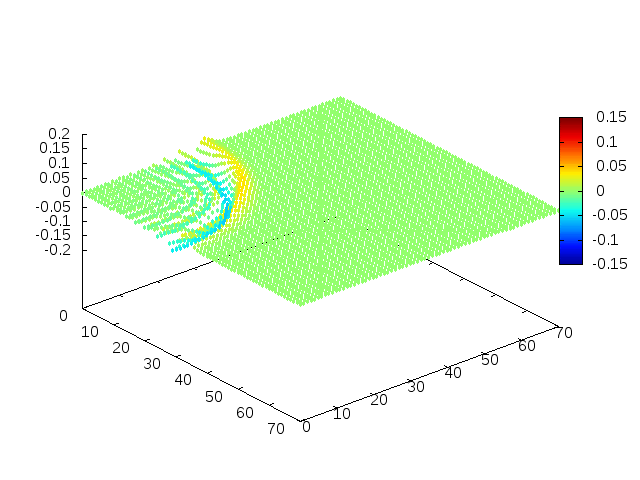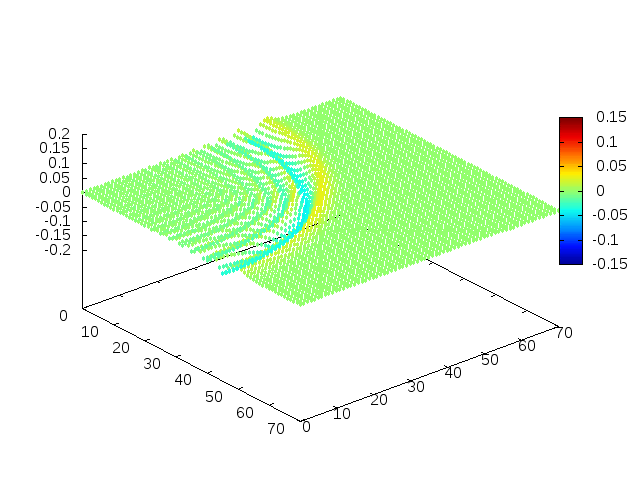
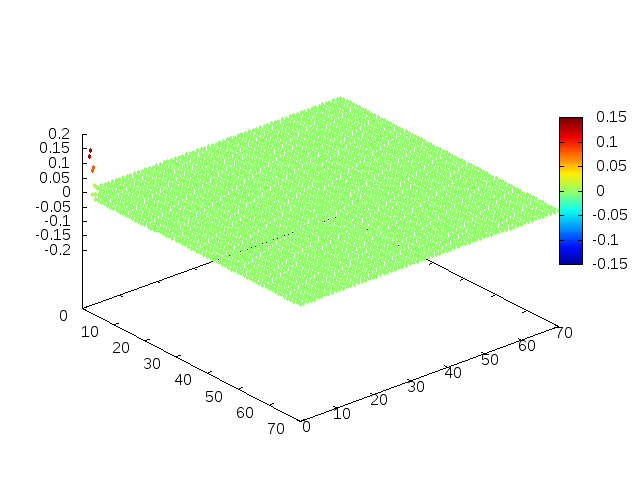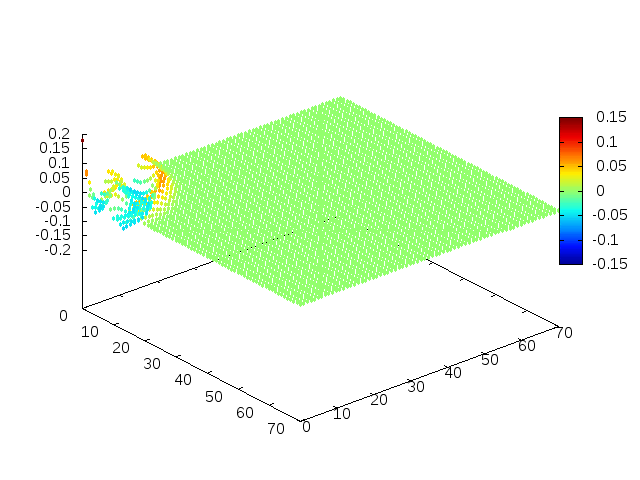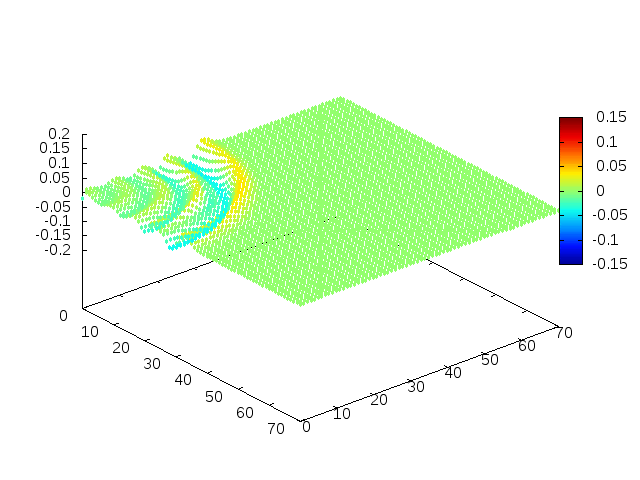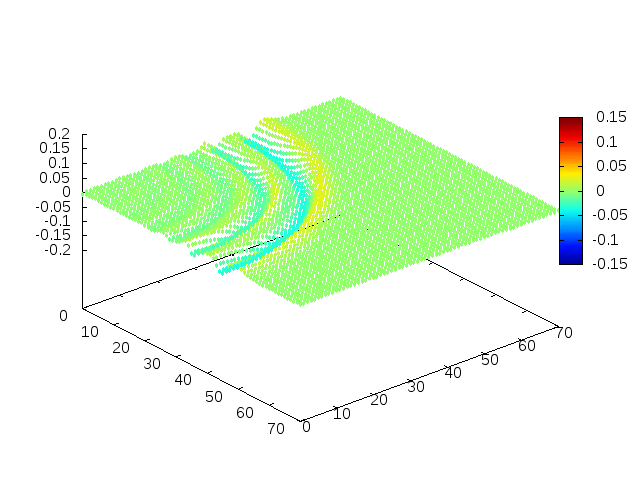
Podemos então, analisar como a mesma condição inicial se porta quando <math>H(x,y) = 1-e^{\frac{-(x^2 + y^2)}{2}}</math>, simulando uma elevação de terra: | |||
[[Arquivo: | [[Arquivo:02cs.gif |frame|500px|center|Simulação em 2D de ondas em águas com gaussiana na origem, visão de cima]] | ||
[[Arquivo: | [[Arquivo:01cs.gif|frame|500px|center|Simulação em 2D de onda em águas com gaussiana na origem, visão em ângulo]] | ||
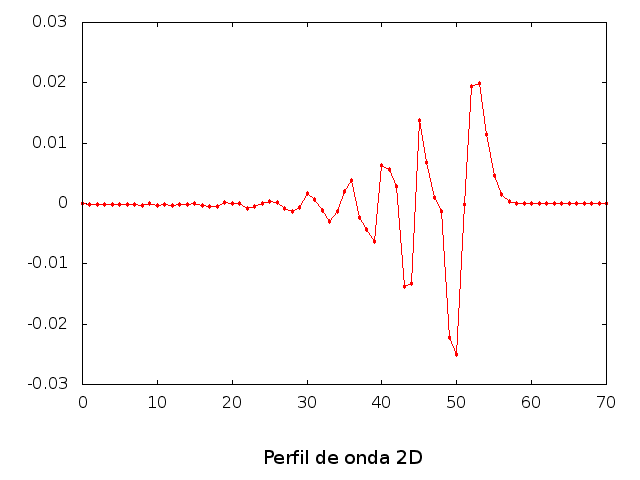
Perfil da onda em sua diagonal: | |||
[[Arquivo:Output_12344.png|frame|500px|center|Perfil da onda em sua diagonal no tempo de simulação igual a 300]] | |||
==Códigos== | |||
===Equação da onda em uma dimensão=== | |||
[[Lax-Friedrichs]] | |||
[[Lax-Wendroff de dois passos]] | |||
[[ | [[Leapfrog]] | ||
[[Erro: Lax-Friedrichs]] | |||
[[Erro: Lax-Wendroff de dois passos]] | |||
[[Erro: Leapfrog]] | |||
===Equação da onda em duas dimensões=== | |||
[[Onda 2D: Leapfrog]] | |||
< | ==Bibliografia== | ||
<references/> | |||
Edição atual tal como às 14h52min de 24 de janeiro de 2018
Integrantes do grupo: Rodrigo Zamin Ferreira (262692), Leonardo Xavier Rodrigues (262696), Maurício Gomes de Queiroz (264889) e Rodrigo Lopes de Sousa Silva (262705)
Introdução
A modelagem numérica vem se tornando cada vez mais uma ferramenta indispensável para um engenheiro. Tal modelagem pode trazer informações importantes para entender como melhor abordar o desenvolvimento de um projeto, neste caso, um que envolva ondas. Nós, como futuros engenheiros físicos, pensamos em trazer um problema mais "concreto", de engenharia costeira e portuária, que pode ou não surgir em nossas vidas profissionais mas cujo método de solução certamente estará presente. Aqui será apresentado um modelo baseado em uma condição inicial e um perfil topográfico do local estudado que descreve a evolução temporal de uma onda.
Inicialmente, para testarmos os diferentes métodos, utilizaremos a equação da onda em uma dimensão, que é uma equação diferencial parcial de segunda ordem, para modelarmos uma corda:
em que é o deslocamento vertical da corda, é a velocidade de propagação da onda e , com o comprimento da corda.
Podemos reescrever a equação da seguinte forma:
.
Uma vez que os métodos citados abaixo são para equações de primeira ordem, é necessário separarmos a equação em um sistema de equações, fazendo a substituição e , de forma que:
Aqui usaremos , sem perda de generalidade. As condições de contorno utilizadas aqui são (pontas fixas), e as condições iniciais são e
Algoritmos
Apresentaremos aqui três abordagens diferentes para a solução da equação diferencial parcial apresentada, e após, seus respectivos erros associados. A respeito das discretizações, corresponde à posição, e representa o tempo.
Método de Lax-Friedrichs
Esse método de ordem [1] consiste em inicialmente discretizar as equações no esquema FTCS (Forward Time Centered Space), ou seja, discretizando a derivada temporal utilizando os tempos e e a derivada espacial através das posições e :
,
.
Resultando em
,
.
Entretanto, ao se realizar uma análise de estabilidade de Von Neumann, conclui-se que esse método é instável[1] . Para torná-lo estável, é necessário trocarmos os termos e por suas médias espaciais, chegando, assim, na expressão do esquema de Lax-Friedrichs:
,
.
Para obtermos o valor de , que é o nosso objetivo, discretizamos a equação
,
Embora as médias espaciais sejam necessárias para a estabilidade do método, elas introduzem um problema: surge um efeito chamado de dissipação numérica, ou seja, a amplitude da solução diminui com o tempo. Isso pode ser observado através da análise de Von Neumann ou de uma investigação da equação do esquema Lax-Friedrichs [1] . Por este método, observa-se que ao inserirmos as médias, mudamos a equação original do problema, pois agora há também um termo do tipo difusivo (uma derivada segunda), com constante de difusão [1].
Agora vamos unir todas as equações, utilizando, além da equação para obtida acima, as discretizações de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v=\frac{\partial u}{\partial t} } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w= \frac{\partial u}{\partial x} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_j^n = \frac{1}{\Delta t} (u_{j}^{n+1} - u_{j}^{n})} ,
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_j^n = \frac{1}{2\Delta x} (u_{j+1}^{n} - u_{j-1}^{n})}
.
Assim, obtemos
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{j}^{n+1} = u_{j}^{n} + \Big( \frac{u_{j-1}^{n} + u_{j+1}^{n}}{2} \Big) - \Big( \frac{u_{j-1}^{n-1} + u_{j+1}^{n-1}}{2} \Big) + \frac{(\Delta t)^2}{4(\Delta x)^2} \Big( u_{j-2}^{n-1} -2u_{j}^{n-1} + u_{j+2}^{n-1}\Big) } .
Método de Leapfrog
Neste método , de ordem Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{O}(\Delta x^2, \Delta t^2 )} [1], utilizamos os pontos intermediários na discretização das equações.
Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} temos
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\Delta t}\bigg( v_{j}^{n+\frac{1}{2}} - v_{j}^{n-\frac{1}{2}}\bigg) = \frac{1}{\Delta x}\Big(w_{j+\frac{1}{2}}^{n} - w_{j-\frac{1}{2}}^{n}\bigg) \Rightarrow v_{j}^{n+\frac{1}{2}} = v_{j}^{n-\frac{1}{2}} + \frac{\Delta t}{\Delta x} \bigg(w_{j+\frac{1}{2}}^{n} - w_{j-\frac{1}{2}}^{n} \bigg) } ,
Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w}
temos
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\Delta x}\bigg(v_{j+1}^{n+\frac{1}{2}} - v_{j}^{n+\frac{1}{2}}\bigg) = \frac{1}{\Delta t}\bigg(w_{j+\frac{1}{2}}^{n+1} - w_{j+\frac{1}{2}}^{n} \bigg) \Rightarrow w_{j+\frac{1}{2}}^{n+1} = w_{j+\frac{1}{2}}^{n} + \frac{\Delta t}{\Delta x} \bigg(v_{j+1}^{n+\frac{1}{2}} - v_{j}^{n+\frac{1}{2}}\bigg) } ,
Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u}
temos
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{j}^{n+\frac{1}{2}} = \frac{\partial u}{\partial t} \bigg|_{j}^{n+\frac{1}{2}} = \frac{1}{\Delta t} (u_{j}^{n+1} - u_j^n) \Rightarrow u_{j}^{n+1} = u_j^n + v_{j}^{n+\frac{1}{2}} \Delta t} ,
Utilizando o fato de que
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{j}^{n+\frac{1}{2}} = \frac{1}{\Delta t} (u_{j}^{n+1} - u_j^n)} ,
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{j+\frac{1}{2}}^{n} = \frac{1}{\Delta x} (u_{j+1}^{n} - u_{j}^{n})}
,
chegamos na equação para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{j}^{n+1}}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{j}^{n+1} = 2u_{j}^{n} - u_{j}^{n-1} + \frac{(\Delta t)^2}{(\Delta x)^2}(u_{j+1}^{n} - 2u_{j}^{n} + u_{j-1}^{n}) }
,
o que é equivalente a discretizarmos a equação da onda diretamente, utilizando que, para uma função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} ,
,
sendo a discretização em .
Método de Lax-Wendroff de Dois Passos
Para este método, de ordem , o primeiro passo consiste em calcular o valor de e utilizando o método de Lax-Friedrichs, para posterior cálculo de e :
,
,
,
,
Agora, no tempo :
,
,
Agrupando as equações,
,
,
E finalmente temos a equação unificada em u, utilizando a expressão para e as discretizações de e , como obtidas na seção sobre o Método de Lax-Friedrichs:
,
Implementação
Ao implementarmos o método, surgem dois problemas: o problema não é auto-inicializável, pois para calcularmos o valor de , necessitamos de (além de ). Entretanto, isto é rapidamente solucionado quando discretizamos a condição inicial de que :
,
ou seja, para o cálculo de , utilizamos que . Através do método de Leapfrog, dessa forma conseguimos isolar :
,
.
Porém, isso não ocorre com os outros dois métodos, pois surgem termos em diferentes posições para o tempo (de , , até ), sendo necessário resolvermos o sistema como um todo simultaneamente, ou seja, teríamos que inverter uma matriz. Por isso, foi utilizado o método de Leapfrog para o cálculo de em todos os métodos, devido a sua simplicidade.
Além disso, são necessários valores de e de , com correspondendo a , para calcularmos e , para qualquer tempo, utilizando os métodos de Lax-Wendroff de dois passos e Lax-Friedrichs. A solução a este problema foi utilizarmos
.
Pensando na condição inicial , e estendendo para além da corda (pensando no seno de ), observamos que ela respeita as equações acima.
Solução e Análise de erros
Primeiramente, apresentamos abaixo as soluções geradas pelos programas, em comparação com a solução analítica.
Aqui já podemos observar o que foi comentado na seção sobre o método de Lax-Friedrichs: devido à dissipação numérica inerente ao método, há uma diminuição da amplitude da onda ao longo do tempo, embora ela mantenha sua forma. Isso interferirá na análise do erro deste método, o que será apresentado na sequência.
A partir do cálulo da solução analítica da equação da onda, podemos calcular quanto o valor obtido pelos métodos difere da solução real, o que leva a uma visualização do erro corrente em cada método de integração.
Nesse caso, a solução é [2].A análise de erros se torna mais evidente durante a escolha do parâmetro , onde . Valores grandes trazem pouca acurácia, e valores pequenos necessitam de muito poder de computação (tempo e dinheiro).
O erro foi obtido efetuando uma média espacial, ou seja, o programa foi evoluindo até um tempo final , e, em , foi feita uma média sobre o valor absoluto da diferença entre a solução analítica e a numérica. Aqui variamos o valor de , fixando , de forma que .
Podemos observar que os erros crescem à medida que o parâmetro k se torna maior, como seria de se esperar.
Além disso, sabendo a ordem do erro dos métodos, podemos determinar a inclinação da reta que melhor se ajusta aos pontos. Se um método tem erro de ordem ,
em que é o erro local, ou seja, o erro de um passo do método, e é uma constante. Assim, o erro global , ou seja, o erro após N passos, é dado por
Como , . Logo, se o erro local é de ordem , o erro global (que é o que calculamos aqui) é de ordem . Além disso, como utilizamos escala logarítmica para representar os resultados, a função do erro global se torna
Ou seja, a inclinação do gráfico do erro global é .
Observamos que se determinarmos a reta que melhor se ajusta às curvas dos métodos de Leapfrog e Lax-Wendroff, ela tem inclinação aproximada de 1, já que os métodos são de ordem Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\Delta t)^2} . Com relação ao gráfico do erro do método de Lax-Friedrichs, é mais complicado de fazer sua análise, uma vez que há o efeito de dissipação numérica, que se intensifica para valores menores de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta t} . Podemos observar nos dados que o ponto de máximo na parte esquerda do gráfico corresponde a um erro de aproximadamente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0,63} , que é a média da solução analítica no tempo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = t_f} (conforme solução analítica, a amplitude no tempo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=100} é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos{\Big(\frac{100\pi}{49}\Big)} \approx 1} , e a média de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin{\Big(\frac{\pi x}{L}\Big)}} vale Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{\pi} \approx 0.64} ). Isso significa que, devido à dissipação, a solução numérica é praticamente 0 frente à solução analítica na parte esquerda do gráfico.
Simulação de Propagação de Onda 2D no Mar Dependente de Topografia
O modelo mais simples para a propagação de onda dependente da topografia parte da equação da onda [3] [4], incluindo uma velocidade dependente da posição, da forma Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle gH(x,y,t)} .
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^2 u}{\partial t^2} = \Big( \frac{\partial}{\partial x} gH(x,y,t) \frac{\partial u}{\partial x}\Big) + \Big( \frac{\partial}{\partial y} gH(x,y,t) \frac{\partial u}{\partial y}\Big) - \frac{\partial^2 H}{\partial t^2} } ,
Sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(x,y,t)}
uma representação da profundidade em águas calmas, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g}
a aceleração da gravidade e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(x, y, t)}
a elevação da água em relação ao nível de águas calmas. Em uma situação real, pode-se obtê-la por mapeamento eletrônico do terreno por sistema de sonar. A dependência em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t}
de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(x,y,t)}
permite um modelo no qual o terreno se modifica com o tempo. Isto é, pode-se observar o efeito que o deslocamento de placas tectônicas, deslizamentos, e até explosões provocam no comportamento das ondas na costa de um país e o reconhecimento de áreas críticas. Entretanto, utilizaremos aqui Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = H(x, y)}
, sem dependência no tempo, e mudaremos as condições iniciais para a modelagem do problema, além de usarmos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g=1}
, para simplificarmos as expressões.
Como primeira abordagem visando uma análise em 2D, a integração da equação em 1D (mesmo sendo uma situação muito idealizada) já traz resultados interessantes. Pode ser mostrado que a velocidade da onda pode ser dada por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v=\sqrt{gH}} , para o caso em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda<<H} , o que é razoável para um tsunami, que tem um comprimento de onda da ordem de até centenas de quilômetros, com uma profundidade da ordem de quilômetros[6]. Como o período da onde não se altera [6], quanto menor a profundidade, menor a velocidade, e menor o seu comprimento de onda. Além disso, devido à conservação de energia, e supondo que a extensão da frente de onda não seja alterada, é obtida a chamada Lei de Green[6]:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{A_2}{A_1} = \Bigg(\frac{H_1}{H_2}\Bigg)^{\frac{1}{4}}}
em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} é a amplitude da onda, e os índices representando dois meios. Logo, quanto menos profundo, maior a amplitude da onda. Esta informação por si só ajuda na construção de proteção contra quebra de ondas, pois é obtido o tamanho que as mesmas atingem. Nos gráficos abaixo podemos observar esses efeitos.
E no caso em que simulamos uma fina camada de líquido, podemos ver a diminuição de velocidade da onda e o aumento de sua amplitude, especialmente no trecho mais à esquerda:
É importante notar o quão poderosa é a integração de equações parciais na vida de um engenheiro.
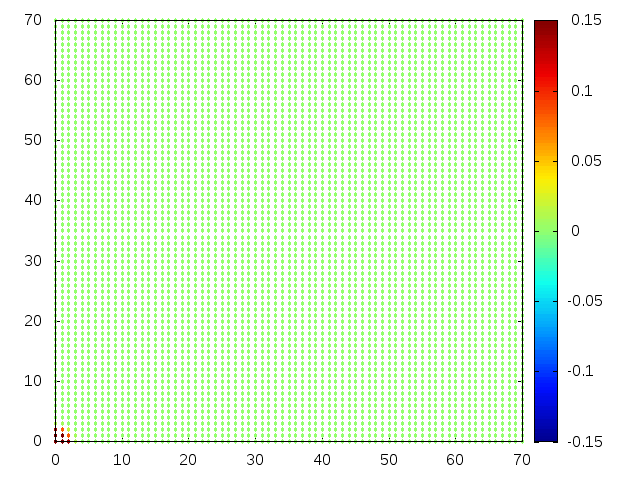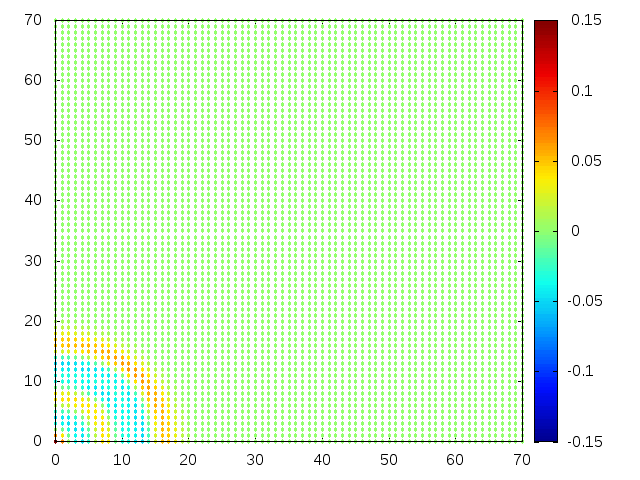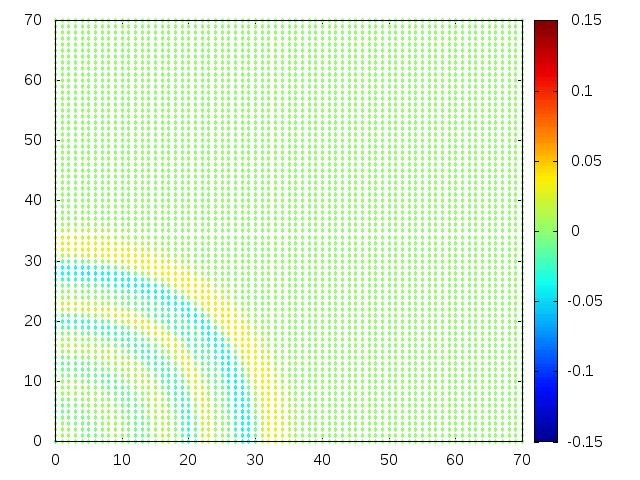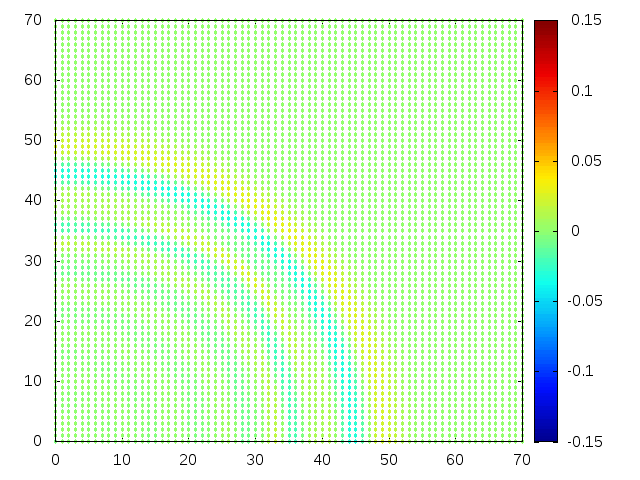
Estendendo o algoritmo de Leapfrog à situação 2D, obtemos, para uma condição inicial de uma gaussiana com média 0 e desvio padrão 1, tanto em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} quanto em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} , e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(x,y) = 1} :
Podemos então, analisar como a mesma condição inicial se porta quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(x,y) = 1-e^{\frac{-(x^2 + y^2)}{2}}}
, simulando uma elevação de terra:
Perfil da onda em sua diagonal:
Códigos
Equação da onda em uma dimensão
Erro: Lax-Wendroff de dois passos
Equação da onda em duas dimensões
Bibliografia
- ↑ 1,0 1,1 1,2 1,3 1,4 Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007). "Numerical Recipes: The Art of Scientific Computing" (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8.
- ↑ Weisstein, Eric W. "Wave Equation--1-Dimensional." From MathWorld--A Wolfram Web Resource; disponível em: [1]; último acesso em 26/11/2017
- ↑ Lie, Knut-Andreas. "The Wave Equation in 1D and 2D". Dept. of Informatics, University of Oslo; disponível em: [2]; último acesso em 23/10/2017.
- ↑ Hjorth-Jensen, Morten. Computational Physics, University of Oslo, 2009.
- ↑ Wadhams, M. J. Doble. "Digital terrain mapping of the underside of sea ice from a small AUV"; disponível em: DOI: 10.1029/2007GL031921 ; último acesso em 23/10/2017.
- ↑ 6,0 6,1 6,2 Silveira, F. L.; Varriale, M. C. "Propagação das ondas marítimas e dos tsunami". Caderno Brasileiro de Ensino de Física, V. 22, N. 2: P. 190-215, 2005.













































![{\displaystyle w_{j}^{n+1}=w_{j}^{n}+{\frac {\Delta t}{\Delta x}}{\Bigg [}{\frac {1}{2}}(v_{j+1}^{n}-v_{j-1}^{n})+{\frac {\Delta t}{2\Delta x}}(w_{j+1}^{n}-2w_{j}^{n}+w_{j-1}^{n}){\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3a64c670bcee4e22ac06f0fd7bfff9e3f055588)
![{\displaystyle v_{j}^{n+1}=v_{j}^{n}+{\frac {\Delta t}{\Delta x}}{\Bigg [}{\frac {1}{2}}(w_{j+1}^{n}-w_{j-1}^{n})+{\frac {\Delta t}{2\Delta x}}(v_{j+1}^{n}-2v_{j}^{n}+v_{j-1}^{n}){\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f320f92413007a3cb3294078873ba6a1fada3e6)


![{\displaystyle u_{j}^{n+1}=2u_{j}^{n}-u_{j}^{n-1}+{\frac {(\Delta t)^{2}}{2(\Delta x)^{2}}}{\Bigg [}{\frac {1}{2}}u_{j+2}^{n-1}-{\frac {1}{2}}u_{j-2}^{n-1}+u_{j+1}^{n}-u_{j+1}^{n-1}-2u_{j}^{n}+u_{j}^{n-1}+u_{j-1}^{n}-u_{j-1}^{n-1}{\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b5c239b890cdd05de6816d2444986009eb19f0f)