Grupo - Lennard Jones: mudanças entre as edições
| (152 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
Alunos: Ben-Hur Cardoso e Vinícius Garcia | |||
<math>U'(r') = 4 \epsilon \left [ \left ( \frac{\sigma}{r'} \right )^{12} | |||
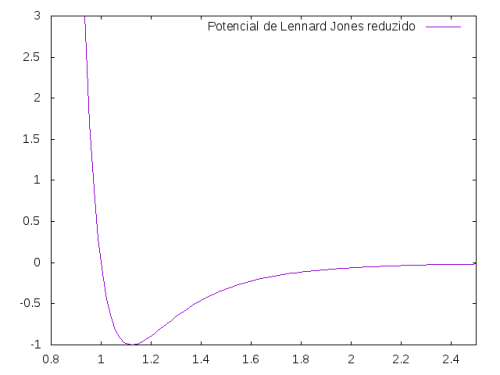
O potencial devido a interação entre duas partículas separadas por uma distância <math>r'</math> pode ser modelado pelo potencial de Lennard-Jones <ref>Lennard-Jones, J. E. (1924), "On the Determination of Molecular Fields", Proc. R. Soc. Lond. A, 106 (738): 463–477</ref>: | |||
<math>U'(r') = 4 \epsilon \left [ \left ( \frac{\sigma}{r'} \right )^{12} - \left ( \frac{\sigma}{r'} \right )^{6} \right ]</math> | |||
Posto em unidades reduzidas (<math>r \equiv r'/ \sigma</math> e <math>U \equiv U' / \epsilon</math>), o potencial reduz-se a: | Posto em unidades reduzidas (<math>r \equiv r'/ \sigma</math> e <math>U \equiv U' / \epsilon</math>), o potencial reduz-se a: | ||
<math>U(r) = 4 \left [ \left ( \frac{1}{r} \right )^{12} | <math>U(r) = 4 \left [ \left ( \frac{1}{r} \right )^{12} - \left ( \frac{1}{r} \right )^{6} \right ]</math> | ||
[[Arquivo:LennardJones.png|500px|center]] | |||
As quantidades físicas de interesse (como pressão, tempo e temperatura) possuem ordens de grandeza muito diferentes entre si quando se usa unidades do Sistema Internacional, o que faz com que fique difícil de identificar erros. Por causa disso, é computacionalmente viável trabalhar com o seguintes sistema de unidades básicas, que mantém os valores em baixas ordens de grandeza: | |||
{| class="wikitable" | {| class="wikitable" | ||
| Linha 30: | Linha 35: | ||
|} | |} | ||
onde <math>m_p</math> é a massa da partícula e <math>k_B</math> é a constante de Boltzmann. | onde <math>m_p</math> é a massa da partícula e <math>k_B</math> é a constante de Boltzmann. | ||
. | |||
Note que as novas unidades são adimensionais. Assim, para comparar o modelo com um sistema físico real, deve-se converter para as unidades desejadas. É interessante notar que a simulação feita utilizando as unidades reduzidas permite visualizar que sistemas distintos serão equivalentes, já que há infinitas combinações de densidade, temperatura, <math>\epsilon </math> e <math>\sigma </math> com mesmas unidades reduzidas. | |||
== Método Monte Carlo == | == Método Monte Carlo == | ||
| Linha 37: | Linha 44: | ||
=== Amostragem simples === | === Amostragem simples === | ||
O cálculo numérico de uma integral utilizando Monte Carlo parte da ideia de que uma integral pode ser reescrita como: | |||
<math> F = \int_a^b{f(x) dx} = (b - a)\langle f(x) \rangle </math> | <math> F = \int_a^b{f(x) dx} = (b - a)\langle f(x) \rangle </math> | ||
Dessa forma, utiliza-se amostragem aleatória massiva para estimar <math> \langle f(x) \rangle </math>, que é a média da função no intervalo de interesse. | Dessa forma, utiliza-se amostragem aleatória massiva para estimar <math> \langle f(x) \rangle </math>, que é a média da função no intervalo de interesse. O estimador para a média real é a média amostral, que por ser uma medida estatística terá sempre um erro inerente associado. | ||
=== Amostragem por importância === | === Amostragem por importância === | ||
Um problema da amostragem simples é que ela utiliza uma distribuição uniforme, que pode, | Um problema da amostragem simples é que ela utiliza uma distribuição uniforme, que pode, para uma função que tenha regiões onde seu valor é próximo de zero por exemplo, custar a estimar corretamente o valor médio da função. A fim de contornar isso, podemos utilizar uma distribuição <math> w(x) </math> tal que a razão <math> \frac{f(x)}{w(x)} </math> seja o mais constante possível. Reescrevendo a integral: | ||
<math> | |||
<math> F = \int_a^b{\frac{f(x)}{w(x)} w(x) dx} = (b - a)\left \langle \frac{f(x)}{w(x)} \right \rangle </math> | |||
Basicamente, é a média dos valores da função razão <math> \frac{f(x)}{w(x)} </math> com distribuição <math> w(x) </math> para sorteio dos pontos. Esse método diminui a variância amostral e faz com que seja muito mais eficiente a convergência do estimador média amostral para a média real da função. | |||
Dado uma amostra com <math>N</math> partículas, a abordagem introduzida por Metropolis segue o seguinte esquema: | === Algoritmo de Metropolis–Hastings === | ||
Dado uma amostra com <math>N</math> partículas, a abordagem introduzida por Metropolis (em 1953, algoritmo para distribuições simétricas) e Hastings (em 1970, algoritmo generalizado) segue o seguinte esquema: | |||
(1) Selecionar uma partícula aleatóriamente, e calcular sua energia <math>U(r)</math>; | (1) Selecionar uma partícula aleatóriamente, e calcular sua energia <math>U(r)</math>; | ||
(2) Dado o deslocamento <math>\mathbf{r_n} = \mathbf{r} + \mathbf{\Delta}</math>, calcular <math>U(r_n)</math>; | (2) Dado o deslocamento <math>\mathbf{r_n} = \mathbf{r} + \mathbf{\Delta}</math>, calcular <math>U(r_n)</math>; | ||
(3) Aceitar o movimento <math>\mathbf{r} \rightarrow \mathbf{r_n}</math> com probabilidade <math>p = min\{1; \exp[-\beta (U(r_n) - U(r))]\}</math> | |||
Devido ao fato das componentes de <math>\mathbf{\Delta}</math> poderem assumir valores postivos e negativos (com a nova posição limitada por alguma condição de contorno), após ser aceito a mudança de posição de uma dada partícula, elá poderá ser selecionada (no próximo passo) com a mesma probabilidade e voltar a sua posição original. Isso garante a condição de balanço detalhado. <ref> Daan Frenkel, Berend Smit, "Understanding molecular simulation: from algorithms to applications"</ref> | |||
=== Estimadores no Equilíbrio === | === Estimadores no Equilíbrio === | ||
Em todos os exemplos tratados aqui, será usado o ensemble NVT (com o número de partículas, volume e temperatura constantes). Dado isso, os sistemas são caracterizados com um densidade e uma temperatura. Com tais | Em todos os exemplos tratados aqui, será usado o ensemble NVT (com o número de partículas, volume e temperatura constantes) com <math>d</math> dimensões. Dado isso, os sistemas são caracterizados com um densidade e uma temperatura. Com tais sistemas no equilíbrio, são estimadas (média de sucessivas medidas) a energia total e a pressão, dadas respectivamente por: | ||
<math>U_T = \sum_i \sum_{j>i}U(r_{ij}) </math> | |||
<math>P = \frac{\rho}{\beta} + \frac{2\rho}{Nd}\sum_i \sum_{j>i}\mathbf{f(\mathbf{r_{ij}})} \cdot \mathbf{r_{ij}} </math> | |||
<math> | onde <math>\mathbf{r_{ij}} = \mathbf{r_{j}} - \mathbf{r_{i}}</math>. Além disso, é interessante a análise da capacidade térmica | ||
<math>C_v = \frac{\langle U_T^2 \rangle - \langle U_T \rangle ^2}{k_BT^2}</math> | |||
<math> | A função radial de distribuição de pares, é uma função que estima o quão provável é encontrar duas partículas a uma distância <math>r</math> dentro de um sistema de várias partículas. Em um sistema de <math>N</math> partículas, o <math>g(r)</math> é definido como a média do número de partículas a uma distância <math>r</math>: | ||
<math> g(r)=\frac{1}{N\rho}\langle\sum_{i=1}^N\sum_{j\neq i}^N\delta(r-|r_i-r_j|) \rangle</math> | |||
A distribuição de densidades é calculada dividindo espacialmente o sistema, no nosso caso de lado <math> L </math>, em <math> M </math> células de lado <math> \frac{L}{M} </math> e acumular em um histograma as densidades das células. Essa medida é relevante para identificação de fases no sistema. | |||
== Detalhes Técnicos== | |||
=== Condições de Contorno === | |||
== | Qualquer sistema possível de ser feito hoje com método Monte Carlo, apesar do grande poder computacional disponível, fica distante do limite termodinâmico. As condições de contorno podem ser estabelecidas de forma a tentar contornar isso. As condições utilizadas neste trabalho foram condições de contorno periódicas, que possibilitam que o sistema se comporte como se fosse muito maior do que é, desde que ele seja isotrópico. | ||
=== Convenção da imagem mínima === | |||
Construindo um sistema cúbico de lado L, com um número N de partículas fixo, as condições de contorno periódicas fazem com a simulação não se limite ao cubo. Ao calcular a interação entre duas partículas, portanto, a distância entre elas não é unívoca, já que há incontáveis cópias de cada uma, repetindo-se periodicamente. Resolve-se esse problema utilizando-se da convenção da imagem mínima, em que é calculada a interação com a imagem mais próxima das outras. | |||
=== Truncamento nas interações === | |||
Um problema da condição de contorno periódica é que, a princípio, cada partícula interagiria com todas as outras do sistema, que devido ao fato de ser periodicamente repetido, seriam infinitas. Como o potencial utilizado é de curto alcance, deve ser possível, de alguma forma, limitar as interações entre as partículas sem perda dos significados numéricos da simulação. Pode-se, então, truncar as interações de uma partícula <math> i </math> a partir de uma distância de corte <math> r_c </math> de forma que há uma descontinuidade no potencial dessa partícula na esfera de raio <math> r_c </math>. | |||
[[Arquivo: mic.png|300px|center]] | |||
Assim o potencial simulado é: | |||
<math> U_{trunc}(r) = \begin{cases}U_{LJ}(r) & , r \leq r_c\\0 & , r > r_c \end{cases} </math> | |||
Esse é o chamado truncamento simples. O subíndice LJ se refere ao potencial de Lennard-Jones. O problema é que isso cria uma contribuição indesejada à pressão, já que há uma força de impulso por conta dessa descontinuidade do potencial. | |||
Pode-se, então, usar o truncamento com deslocamento, que evita essa descontinuidade fazendo uma subtração em todo ponto do módulo do potencial de Lennard-Jones à distância <math> r_c </math>. Assim, o potencial simulado é: | |||
= | <math> U_{deslocado}(r) = \begin{cases}U_{LJ}(r) - U_{LJ}(r_c) & , r \leq r_c\\0 & , r > r_c \end{cases} </math> | ||
Com esse potencial, que é contínuo, as forças serão sempre finitas, o que retira a força de impulso que alteraria medidas de pressão. | |||
=== Translação === | === Translação === | ||
== | A possível nova posição de uma partícula será <math>(x_n, y_n, z_n)</math> tal que | ||
<math> x_n = x + \Delta (\alpha - 0.5)</math> | |||
<math> y_n = y + \Delta (\alpha - 0.5)</math> | |||
<math> z_n = z + \Delta (\alpha - 0.5)</math> | |||
sendo <math>\alpha</math> números aleatórios uniformemente distribuídos e <math> \Delta </math> o deslocamento máximo permitido. Se a nova posição for aceita seguindo o algorítmo de Metropolis, a partícula assumirá essa posição. Caso contrário, a antiga configuração contribuirá novamente na média. <ref> David P. Landau, Kurt Binder, "A Guide to Monte Carlo Simulations in Statistical Physics"</ref> | |||
O tamanho de <math> \Delta </math> não pode ser grande ao ponto de nunca ser aceito nem pequeno ao ponto de sempre ser aceito. Dado isso, buscando uma taxa de aceitação <math> \eta </math> entre <math> 30 \%</math> e <math> 50 \% </math>, define-se um <math> \Delta_0 </math> inicial que vai se ajustando no decorrer da simulação, executando - a cada passo Monte Carlo (<math>N</math> passos de simulação) - o seguinte algorítimo: | |||
Se (<math> \eta < 0.3 </math>): <math> \Delta \leftarrow \Delta \times (\eta / 0.3)</math> | |||
Se (<math> \eta > 0.5 </math>): <math> \Delta \leftarrow \Delta \times (\eta / 0.5)</math> | |||
== Sistema bidimensional == | |||
Dado um sistema com densidade <math> \rho = N / L^2 </math> e temperatura <math>T</math>, os sistemas foram feitos com: | |||
(A) <math> N = 256 </math> partículas | |||
(B) Quadrado de lado <math> L = (N / \rho)^{1/2} </math>, utilizando a convenção da imagem mínima | |||
(C) Incialização aleatória | |||
(D) Distância de corte <math>r_c = 2.5 \sigma</math> | |||
(E) Deslocamento máximo inicial <math>\Delta_0 = L/2 </math> | |||
=== Transição de fase líquido-gás === | |||
A partir do artigo de M Rovere et al <ref> M Rovere et al (1990) "The gas-liquid transition of the two-dimensional Lennard-Jones fluid". J. Phys.: Condens. Matter 2 7009 </ref>, que modelou o sistema apresentado, obtemos a informação da temperatura e da densidade críticas. Os valores encontrados pelos autores do artigo são <math> T = 0.5</math> e <math> \rho = 0.3 </math>, que determinam qual intervalo de valores de temperatura e densidade apresentam coexistência de fases distintas. | |||
=== Transição de fase com densidade fixa === | |||
Fixada a densidade <math> \rho = 0.3 </math>, foram realizadas simulações para as diferentes temperaturas <math> T \in \{0.45, 0.50, 0.70\}</math>. | |||
Evolução temporal da Energia Total: | |||
[[Arquivo:time_evolution_U_d_03.png|500px|center]] | |||
Observa-se que o sistema se encontra em equilíbrio a <math>10^5</math> passos Monte Carlo. Isso é corroborado pelos resultados do artigo de M Rovere et al. A partir do sistema equilibrado, são analisadas a distribuição de densidade e a função distribuição de pares para verificar a presença de uma (líquida) ou duas fases (líquida, gasosa), usando uma média de <math>10^5</math> medidas sucessivas. | |||
Para <math> T = 0.70</math> temos que: | |||
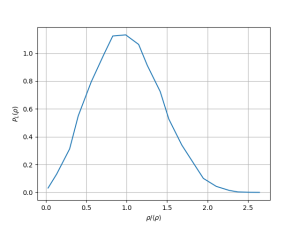
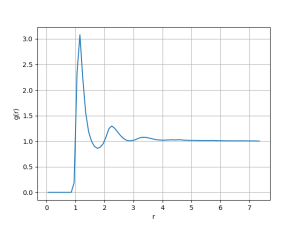
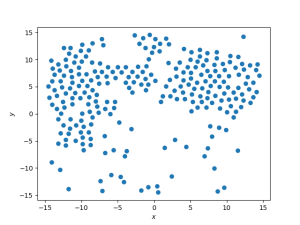
[[Arquivo: snapshot_t70_d_03.png|300px]] [[Arquivo: P_t70_d_03.png|300px]] [[Arquivo: g_t70_d_03.png|300px]] | |||
Nesse caso observa-se apenas uma fase, com a densidade média sendo a densidade global do sistema, que é diferente do centro do pico (<math> \rho \approx 1.0 </math>). Isso caracteriza a fase gasosa, que ocupa todo o espaço disponível. A função distribuição de pares rapidamente converge para 1 com pequenas oscilações, caracterizando um gás de alta densidade. | |||
Para <math> T = 0.50</math> temos que: | |||
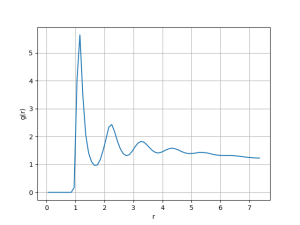
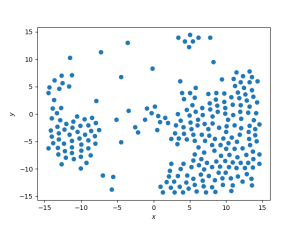
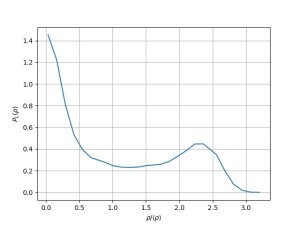
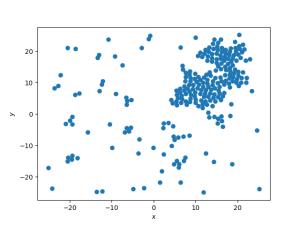
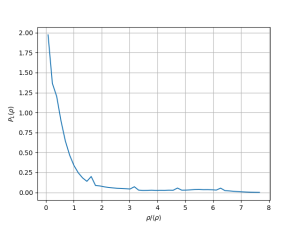
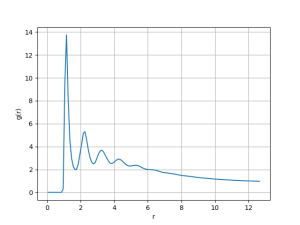
[[Arquivo: snapshot_t50_d_03.png|300px]] [[Arquivo: P_t50_d_03.png|300px]] [[Arquivo: g_t50_d_03.png|300px]] | |||
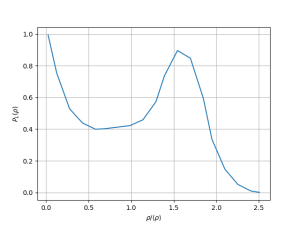
Nesse caso observa-se a coexistência das fases gasosa e líquida. Além disso, pode-se observar a densidade característica aproximada de cada fase a essa temperatura centrada nos respectivos picos (<math> \rho_g \approx 0.2 </math> e <math> \rho_l \approx 2.0 </math>). A função distribuição de pares representa a de uma fase líquida. | |||
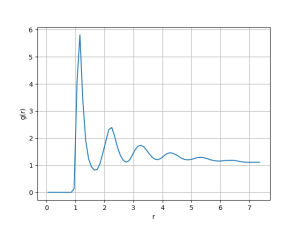
Para <math> T = 0.45</math> temos que: | |||
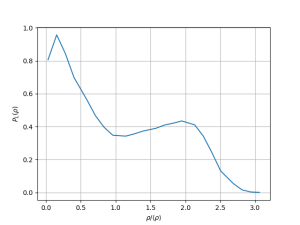
[[Arquivo: snapshot_t45_d_03.png|300px]] [[Arquivo: P_t45_d_03.png|300px]] [[Arquivo: g_t45_d_03.png|300px]] | |||
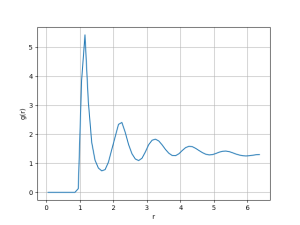
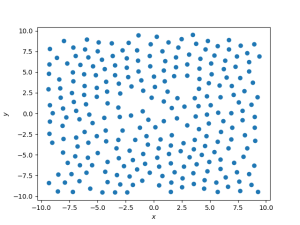
Nesse gráfico a primeira impressão é de coexistência de fases. Apesar disso, densidade zero não corresponde a uma fase real, e sim aos espaços vazios. Dessa forma, a fase aqui é a líquida. O ''snapshot'' permite visualizar isso, já que há aglomerados de densidade aparentemente constante separados por espaços praticamente sem partículas. A densidade da fase líquida a essa temperatura é aproximadamente o centro do pico da direita (<math> \rho \approx 2.3 </math>). | |||
Para <math> T = 0.30</math> temos que: | |||
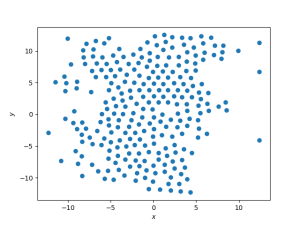
[[Arquivo: snapshot_t30_d_03.png|300px]] [[Arquivo: P_t30_d_03.png|300px]] [[Arquivo: g_t30_d_03.png|300px]] | |||
Assim como no gráfico anterior, há dois picos mas apenas um representa uma fase. A principal diferença é que o pico em zero é bem maior e mais agudo que no caso <math> T = 0.45</math>, o que ilustra que há mais espaço vazio. A densidade do líquido aqui é <math> \rho \approx 2.8 </math>. Nota-se que o sistema parece estar se organizando numa fase hexagonal, apesar de ainda ser amorfa, e a densidade já é bem mais alta. A distribuição de pares tem mínimos bem menores do que para os parâmetros acima tratados, caracterizando um sistema que parece estar próximo da transição para a fase hexagonal de baixa energia. | |||
De maneira geral, é possível estimar o intervalo de parâmetros para o qual ocorre a transição de fase líquido-gás. É possível, também, visualizar, a partir da distribuição de densidades, a coexistência de fases, já que cada estado tem uma densidade média característica a dada temperatura. | |||
=== Transição de fase com temperatura fixa === | |||
Dado a temperatura fixa <math> T = 0.45 </math>, é observado o sistema para as diferentes densidades <math> \rho \in \{0.10, 0.30, 0.40\}</math>. | |||
Evolução temporal da Energia Total: | |||
[[Arquivo:time_evolution_U_T_45.png|500px|center]] | |||
Observa-se que o sistema se encontra em equilíbrio a <math>10^5</math> passos Monte Carlo. Isso é corroborado pelos resultados do artigo de M Rovere et al. A partir do sistema equilibrado, são analisadas a distribuição de densidade e a função distribuição de pares para verificar a presença de uma (líquida) ou duas fases (líquida, gasosa), usando uma média de <math>10^5</math> medidas sucessivas. | |||
Para <math> \rho = 0.10</math> temos que: | |||
[[Arquivo: snapshot_t45_d_10.png|300px]] [[Arquivo: P_t45_d_10.png|300px]] [[Arquivo: g_t45_d_10.png|300px]] | |||
Observa-se no ''snapshot'' que o sistema parece ter fase líquida e fase gasosa coexistindo. O resultado da distribuição de densidades pode ter sido afetado pelo aumento da área (consequentemente também das células usadas para realização do histograma) já que o sistema ficou maior a fim de diminuir a densidade mantendo o número de partículas. Apesar disso, o resultado da função distribuição de pares parece razoável com a hipótese da fase líquida estar presente. | |||
Para <math> \rho = 0.30</math> temos que: | |||
[[Arquivo: snapshot_t45_d_03.png|300px]] [[Arquivo: P_t45_d_03.png|300px]] [[Arquivo: g_t45_d_03.png|300px]] | |||
Esse gráfico foi tratado anteriormente (para temperatura fixa) e está reproduzido novamente a fim de comparação. | |||
Para <math> \rho = 0.40</math> temos que: | |||
[[Arquivo: snapshot_t45_d_40.png|300px]] [[Arquivo: P_t45_d_40.png|300px]] [[Arquivo: g_t45_d_40.png|300px]] | |||
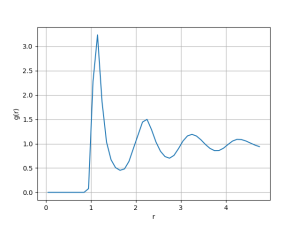
Nesse sistema há a presença de fase líquida com menos espaços vazios. O pico de densidade da fase líquida situa-se em <math> \rho \approx 1.5 </math>. Essa queda da densidade do líquido com aumento da densidade do sistema indica que uma transição de fase para gás pode estar próxima para esses parâmetros. | |||
Para <math> \rho = 0.70</math> temos que: | |||
[[Arquivo: snapshot_t45_d_70.png|300px]] [[Arquivo: P_t45_d_70.png|300px]] [[Arquivo: g_t45_d_70.png|300px]] | |||
Observa-se que o sistema tem relativa homogeneidade e ocupa toda a área. Isso se caracteriza como um gás, como pode ser verificado na distribuição de densidade, que tem apenas um pico em <math> \rho \approx 1.0 </math> (que não é a média global). Apesar disso, o sistema parece relativamente organizado, o que sugere uma possível transição de fase. Também sugere isso a distribuição de pares, que tem mínimos baixos que remetem à fase sólida. | |||
== Sistema tridimensional == | |||
Dado um sistema tridimensional com densidade <math> \rho = N / L^3</math> e temperatura <math>T</math>, os diagramas foram feitos com: | |||
(A) <math> N = 500 </math> partículas | |||
(B) Cubo de lado <math> L = (N / \rho)^{1/3} </math> com convenção da imagem mínima | |||
(C) Incialização aleatória | |||
(D) Distância de corte <math>r_c \in \{2.5 \sigma, 3.0 \sigma, 3.5 \sigma \} </math> | |||
(E) Deslocamento máximo inicial <math>\Delta_0 = L/2 </math> | |||
=== Transição de fase líquido-gás === | |||
Conforme o trabalho desenvolvido por Nicholas et al <ref>J.J. Nicolas, K.E. Gubbins, W.B. Streett, and D.J. Tildesley (1979). "Equation of state for | |||
the Lennard-Jones fluid". Mol. Phys., 37</ref>, os valores críticos na transição de fase líquido-gás para um fluido de Lennard-Jones tridimensional são <math>T_{cr} = 1.35</math> e <math>\rho_{cr} = 0.35</math>. | |||
=== T = 2.0 (acima do valor crítico)=== | |||
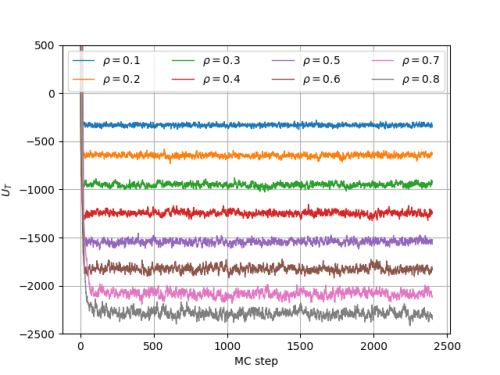
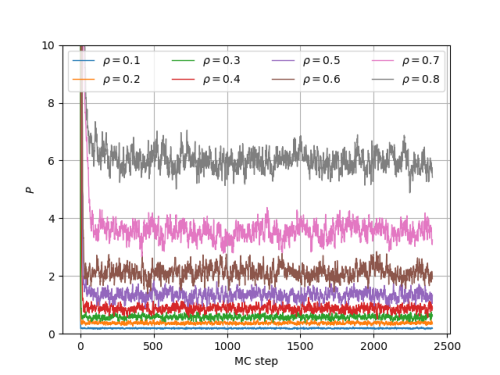
Tendo em vista que a análise no equilíbrio do sistema bidimensional foi feita após <math> 10^5 </math> passos Monte Carlo, é bastante possível que os sistemas tridimensionais aqui tratados não tenham alcançado o equilíbrio. Para <math>r_c = 2.5\sigma</math>, temos a evolução temporal da energia total e da pressão: | |||
[[Arquivo: t_t20_r25_U.png|500px]] [[Arquivo: t_t20_r25_P.png|500px]] | |||
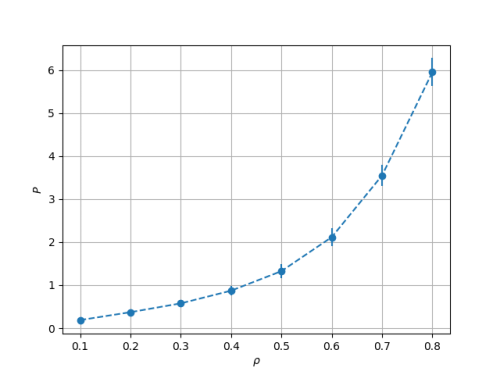
Estimando seus valores a partir do equilíbrio, determina-se o diagrama de fase: | |||
[[Arquivo:t20_r25_Pd.png|500px|center]] | |||
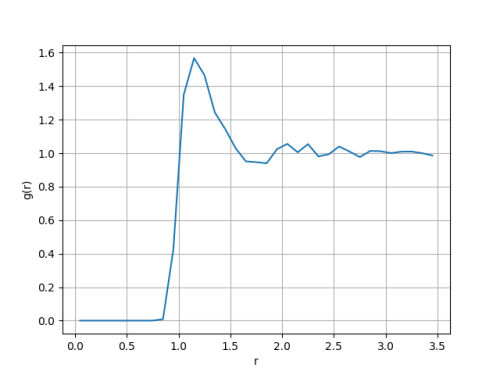
Além disso, tem-se as diferentes configurações espaciais para as densidades <math>\rho = 0.2</math> e <math>\rho = 0.6</math>, respectivamente: | |||
[[Arquivo:g_t20_d02_r25.png|500px]] [[Arquivo:g_t20_d06_r25.png|500px]] | |||
Executando o mesmo esquema, o diagrama é comparado para diferentes valores de <math>r_c</math>: | |||
[[Arquivo:t20_Pd.png|500px|center]] | |||
Nessa situação (acima do valor crítico de temperatura), o gráfico pressão - densidade mostra sua injetividade, e portanto, a não coexistência de fases (como esperado). | |||
==Referências== | ==Referências== | ||
<references /> | |||
Edição atual tal como às 07h48min de 23 de janeiro de 2018
Alunos: Ben-Hur Cardoso e Vinícius Garcia
O potencial devido a interação entre duas partículas separadas por uma distância Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r'}
pode ser modelado pelo potencial de Lennard-Jones [1]:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U'(r') = 4 \epsilon \left [ \left ( \frac{\sigma}{r'} \right )^{12} - \left ( \frac{\sigma}{r'} \right )^{6} \right ]}
Posto em unidades reduzidas (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r \equiv r'/ \sigma} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U \equiv U' / \epsilon} ), o potencial reduz-se a:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(r) = 4 \left [ \left ( \frac{1}{r} \right )^{12} - \left ( \frac{1}{r} \right )^{6} \right ]}
As quantidades físicas de interesse (como pressão, tempo e temperatura) possuem ordens de grandeza muito diferentes entre si quando se usa unidades do Sistema Internacional, o que faz com que fique difícil de identificar erros. Por causa disso, é computacionalmente viável trabalhar com o seguintes sistema de unidades básicas, que mantém os valores em baixas ordens de grandeza:
| Grandeza | Comprimento | Tempo | Massa | Temperatura | Energia | Pressão | Densidade |
|---|---|---|---|---|---|---|---|
| Unidade | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma \sqrt{m_p / \epsilon}} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_p} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon/k_B} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon / \sigma^3} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 / \sigma^{3}} |
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_p} é a massa da partícula e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B} é a constante de Boltzmann.
Note que as novas unidades são adimensionais. Assim, para comparar o modelo com um sistema físico real, deve-se converter para as unidades desejadas. É interessante notar que a simulação feita utilizando as unidades reduzidas permite visualizar que sistemas distintos serão equivalentes, já que há infinitas combinações de densidade, temperatura, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma } com mesmas unidades reduzidas.
Método Monte Carlo
Denomina-se método de Monte Carlo métodos estatísticos que se baseiam em amostragem aleatória massiva para cálculo numérico.
Amostragem simples
O cálculo numérico de uma integral utilizando Monte Carlo parte da ideia de que uma integral pode ser reescrita como:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = \int_a^b{f(x) dx} = (b - a)\langle f(x) \rangle }
Dessa forma, utiliza-se amostragem aleatória massiva para estimar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle f(x) \rangle } , que é a média da função no intervalo de interesse. O estimador para a média real é a média amostral, que por ser uma medida estatística terá sempre um erro inerente associado.
Amostragem por importância
Um problema da amostragem simples é que ela utiliza uma distribuição uniforme, que pode, para uma função que tenha regiões onde seu valor é próximo de zero por exemplo, custar a estimar corretamente o valor médio da função. A fim de contornar isso, podemos utilizar uma distribuição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w(x) } tal que a razão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{f(x)}{w(x)} } seja o mais constante possível. Reescrevendo a integral:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = \int_a^b{\frac{f(x)}{w(x)} w(x) dx} = (b - a)\left \langle \frac{f(x)}{w(x)} \right \rangle }
Basicamente, é a média dos valores da função razão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{f(x)}{w(x)} }
com distribuição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w(x) }
para sorteio dos pontos. Esse método diminui a variância amostral e faz com que seja muito mais eficiente a convergência do estimador média amostral para a média real da função.
Algoritmo de Metropolis–Hastings
Dado uma amostra com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} partículas, a abordagem introduzida por Metropolis (em 1953, algoritmo para distribuições simétricas) e Hastings (em 1970, algoritmo generalizado) segue o seguinte esquema:
(1) Selecionar uma partícula aleatóriamente, e calcular sua energia Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(r)}
;
(2) Dado o deslocamento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r_n} = \mathbf{r} + \mathbf{\Delta}}
, calcular Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(r_n)}
;
(3) Aceitar o movimento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r} \rightarrow \mathbf{r_n}}
com probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle p = min\{1; \exp[-\beta (U(r_n) - U(r))]\}}
Devido ao fato das componentes de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\Delta}} poderem assumir valores postivos e negativos (com a nova posição limitada por alguma condição de contorno), após ser aceito a mudança de posição de uma dada partícula, elá poderá ser selecionada (no próximo passo) com a mesma probabilidade e voltar a sua posição original. Isso garante a condição de balanço detalhado. [2]
Estimadores no Equilíbrio
Em todos os exemplos tratados aqui, será usado o ensemble NVT (com o número de partículas, volume e temperatura constantes) com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle d} dimensões. Dado isso, os sistemas são caracterizados com um densidade e uma temperatura. Com tais sistemas no equilíbrio, são estimadas (média de sucessivas medidas) a energia total e a pressão, dadas respectivamente por:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_T = \sum_i \sum_{j>i}U(r_{ij}) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \frac{\rho}{\beta} + \frac{2\rho}{Nd}\sum_i \sum_{j>i}\mathbf{f(\mathbf{r_{ij}})} \cdot \mathbf{r_{ij}} }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r_{ij}} = \mathbf{r_{j}} - \mathbf{r_{i}}} . Além disso, é interessante a análise da capacidade térmica
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_v = \frac{\langle U_T^2 \rangle - \langle U_T \rangle ^2}{k_BT^2}}
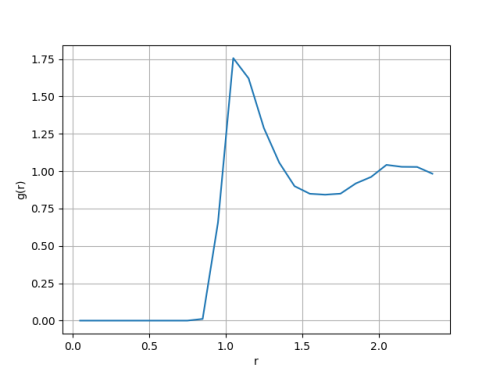
A função radial de distribuição de pares, é uma função que estima o quão provável é encontrar duas partículas a uma distância Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} dentro de um sistema de várias partículas. Em um sistema de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} partículas, o Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(r)} é definido como a média do número de partículas a uma distância Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(r)=\frac{1}{N\rho}\langle\sum_{i=1}^N\sum_{j\neq i}^N\delta(r-|r_i-r_j|) \rangle}
A distribuição de densidades é calculada dividindo espacialmente o sistema, no nosso caso de lado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L } , em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle M } células de lado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{L}{M} } e acumular em um histograma as densidades das células. Essa medida é relevante para identificação de fases no sistema.
Detalhes Técnicos
Condições de Contorno
Qualquer sistema possível de ser feito hoje com método Monte Carlo, apesar do grande poder computacional disponível, fica distante do limite termodinâmico. As condições de contorno podem ser estabelecidas de forma a tentar contornar isso. As condições utilizadas neste trabalho foram condições de contorno periódicas, que possibilitam que o sistema se comporte como se fosse muito maior do que é, desde que ele seja isotrópico.
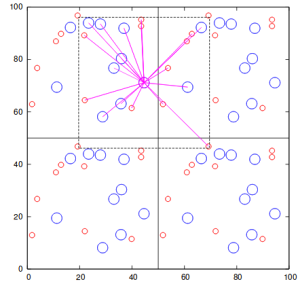
Convenção da imagem mínima
Construindo um sistema cúbico de lado L, com um número N de partículas fixo, as condições de contorno periódicas fazem com a simulação não se limite ao cubo. Ao calcular a interação entre duas partículas, portanto, a distância entre elas não é unívoca, já que há incontáveis cópias de cada uma, repetindo-se periodicamente. Resolve-se esse problema utilizando-se da convenção da imagem mínima, em que é calculada a interação com a imagem mais próxima das outras.
Truncamento nas interações
Um problema da condição de contorno periódica é que, a princípio, cada partícula interagiria com todas as outras do sistema, que devido ao fato de ser periodicamente repetido, seriam infinitas. Como o potencial utilizado é de curto alcance, deve ser possível, de alguma forma, limitar as interações entre as partículas sem perda dos significados numéricos da simulação. Pode-se, então, truncar as interações de uma partícula Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } a partir de uma distância de corte Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_c } de forma que há uma descontinuidade no potencial dessa partícula na esfera de raio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_c } .
Assim o potencial simulado é:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{trunc}(r) = \begin{cases}U_{LJ}(r) & , r \leq r_c\\0 & , r > r_c \end{cases} }
Esse é o chamado truncamento simples. O subíndice LJ se refere ao potencial de Lennard-Jones. O problema é que isso cria uma contribuição indesejada à pressão, já que há uma força de impulso por conta dessa descontinuidade do potencial.
Pode-se, então, usar o truncamento com deslocamento, que evita essa descontinuidade fazendo uma subtração em todo ponto do módulo do potencial de Lennard-Jones à distância Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_c } . Assim, o potencial simulado é:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{deslocado}(r) = \begin{cases}U_{LJ}(r) - U_{LJ}(r_c) & , r \leq r_c\\0 & , r > r_c \end{cases} }
Com esse potencial, que é contínuo, as forças serão sempre finitas, o que retira a força de impulso que alteraria medidas de pressão.
Translação
A possível nova posição de uma partícula será Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_n, y_n, z_n)} tal que
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_n = x + \Delta (\alpha - 0.5)}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_n = y + \Delta (\alpha - 0.5)}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_n = z + \Delta (\alpha - 0.5)}
sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} números aleatórios uniformemente distribuídos e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta } o deslocamento máximo permitido. Se a nova posição for aceita seguindo o algorítmo de Metropolis, a partícula assumirá essa posição. Caso contrário, a antiga configuração contribuirá novamente na média. [3]
O tamanho de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta } não pode ser grande ao ponto de nunca ser aceito nem pequeno ao ponto de sempre ser aceito. Dado isso, buscando uma taxa de aceitação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta } entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 30 \%} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 50 \% } , define-se um Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta_0 } inicial que vai se ajustando no decorrer da simulação, executando - a cada passo Monte Carlo (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} passos de simulação) - o seguinte algorítimo:
Se (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta < 0.3 }
): Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \leftarrow \Delta \times (\eta / 0.3)}
Se (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta > 0.5 }
): Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \leftarrow \Delta \times (\eta / 0.5)}
Sistema bidimensional
Dado um sistema com densidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = N / L^2 } e temperatura Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} , os sistemas foram feitos com:
(A) Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = 256 }
partículas
(B) Quadrado de lado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = (N / \rho)^{1/2} }
, utilizando a convenção da imagem mínima
(C) Incialização aleatória
(D) Distância de corte Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_c = 2.5 \sigma}
(E) Deslocamento máximo inicial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta_0 = L/2 }
Transição de fase líquido-gás
A partir do artigo de M Rovere et al [4], que modelou o sistema apresentado, obtemos a informação da temperatura e da densidade críticas. Os valores encontrados pelos autores do artigo são Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 0.5} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = 0.3 } , que determinam qual intervalo de valores de temperatura e densidade apresentam coexistência de fases distintas.
Transição de fase com densidade fixa
Fixada a densidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = 0.3 } , foram realizadas simulações para as diferentes temperaturas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \in \{0.45, 0.50, 0.70\}} .
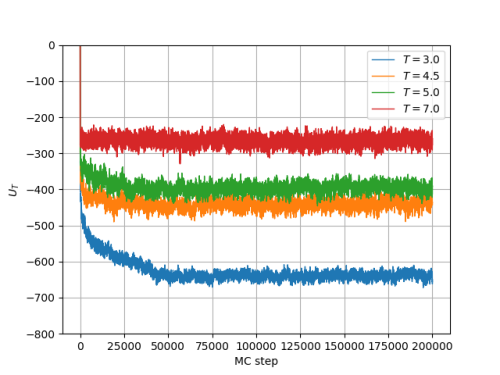
Evolução temporal da Energia Total:
Observa-se que o sistema se encontra em equilíbrio a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^5} passos Monte Carlo. Isso é corroborado pelos resultados do artigo de M Rovere et al. A partir do sistema equilibrado, são analisadas a distribuição de densidade e a função distribuição de pares para verificar a presença de uma (líquida) ou duas fases (líquida, gasosa), usando uma média de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^5} medidas sucessivas.
Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 0.70} temos que:
Nesse caso observa-se apenas uma fase, com a densidade média sendo a densidade global do sistema, que é diferente do centro do pico (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho \approx 1.0 } ). Isso caracteriza a fase gasosa, que ocupa todo o espaço disponível. A função distribuição de pares rapidamente converge para 1 com pequenas oscilações, caracterizando um gás de alta densidade.
Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 0.50} temos que:
Nesse caso observa-se a coexistência das fases gasosa e líquida. Além disso, pode-se observar a densidade característica aproximada de cada fase a essa temperatura centrada nos respectivos picos (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_g \approx 0.2 } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_l \approx 2.0 } ). A função distribuição de pares representa a de uma fase líquida.
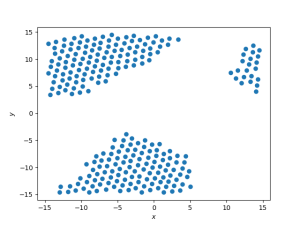
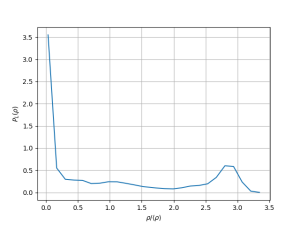
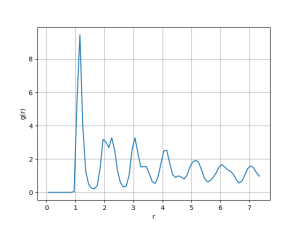
Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 0.45} temos que:
Nesse gráfico a primeira impressão é de coexistência de fases. Apesar disso, densidade zero não corresponde a uma fase real, e sim aos espaços vazios. Dessa forma, a fase aqui é a líquida. O snapshot permite visualizar isso, já que há aglomerados de densidade aparentemente constante separados por espaços praticamente sem partículas. A densidade da fase líquida a essa temperatura é aproximadamente o centro do pico da direita (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho \approx 2.3 } ).
Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 0.30} temos que:
Assim como no gráfico anterior, há dois picos mas apenas um representa uma fase. A principal diferença é que o pico em zero é bem maior e mais agudo que no caso Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 0.45} , o que ilustra que há mais espaço vazio. A densidade do líquido aqui é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho \approx 2.8 } . Nota-se que o sistema parece estar se organizando numa fase hexagonal, apesar de ainda ser amorfa, e a densidade já é bem mais alta. A distribuição de pares tem mínimos bem menores do que para os parâmetros acima tratados, caracterizando um sistema que parece estar próximo da transição para a fase hexagonal de baixa energia.
De maneira geral, é possível estimar o intervalo de parâmetros para o qual ocorre a transição de fase líquido-gás. É possível, também, visualizar, a partir da distribuição de densidades, a coexistência de fases, já que cada estado tem uma densidade média característica a dada temperatura.
Transição de fase com temperatura fixa
Dado a temperatura fixa Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 0.45 } , é observado o sistema para as diferentes densidades Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho \in \{0.10, 0.30, 0.40\}} .
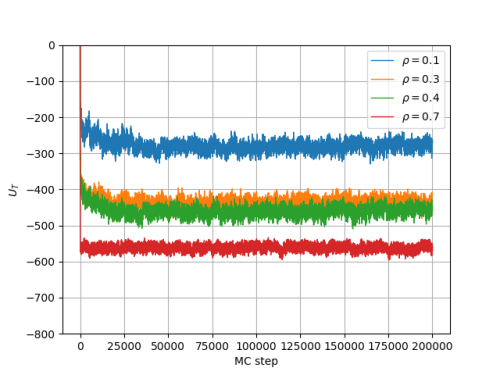
Evolução temporal da Energia Total:
Observa-se que o sistema se encontra em equilíbrio a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^5}
passos Monte Carlo. Isso é corroborado pelos resultados do artigo de M Rovere et al. A partir do sistema equilibrado, são analisadas a distribuição de densidade e a função distribuição de pares para verificar a presença de uma (líquida) ou duas fases (líquida, gasosa), usando uma média de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^5}
medidas sucessivas.
Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = 0.10} temos que:
Observa-se no snapshot que o sistema parece ter fase líquida e fase gasosa coexistindo. O resultado da distribuição de densidades pode ter sido afetado pelo aumento da área (consequentemente também das células usadas para realização do histograma) já que o sistema ficou maior a fim de diminuir a densidade mantendo o número de partículas. Apesar disso, o resultado da função distribuição de pares parece razoável com a hipótese da fase líquida estar presente.
Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = 0.30} temos que:
Esse gráfico foi tratado anteriormente (para temperatura fixa) e está reproduzido novamente a fim de comparação.
Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = 0.40} temos que:
Nesse sistema há a presença de fase líquida com menos espaços vazios. O pico de densidade da fase líquida situa-se em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho \approx 1.5 } . Essa queda da densidade do líquido com aumento da densidade do sistema indica que uma transição de fase para gás pode estar próxima para esses parâmetros.
Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = 0.70} temos que:
Observa-se que o sistema tem relativa homogeneidade e ocupa toda a área. Isso se caracteriza como um gás, como pode ser verificado na distribuição de densidade, que tem apenas um pico em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho \approx 1.0 } (que não é a média global). Apesar disso, o sistema parece relativamente organizado, o que sugere uma possível transição de fase. Também sugere isso a distribuição de pares, que tem mínimos baixos que remetem à fase sólida.
Sistema tridimensional
Dado um sistema tridimensional com densidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = N / L^3} e temperatura Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} , os diagramas foram feitos com:
(A) Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = 500 }
partículas
(B) Cubo de lado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = (N / \rho)^{1/3} }
com convenção da imagem mínima
(C) Incialização aleatória
(D) Distância de corte Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_c \in \{2.5 \sigma, 3.0 \sigma, 3.5 \sigma \} }
(E) Deslocamento máximo inicial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta_0 = L/2 }
Transição de fase líquido-gás
Conforme o trabalho desenvolvido por Nicholas et al [5], os valores críticos na transição de fase líquido-gás para um fluido de Lennard-Jones tridimensional são Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{cr} = 1.35} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{cr} = 0.35} .
T = 2.0 (acima do valor crítico)
Tendo em vista que a análise no equilíbrio do sistema bidimensional foi feita após Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^5 } passos Monte Carlo, é bastante possível que os sistemas tridimensionais aqui tratados não tenham alcançado o equilíbrio. Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_c = 2.5\sigma} , temos a evolução temporal da energia total e da pressão:
Estimando seus valores a partir do equilíbrio, determina-se o diagrama de fase:
Além disso, tem-se as diferentes configurações espaciais para as densidades Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = 0.2} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = 0.6} , respectivamente:
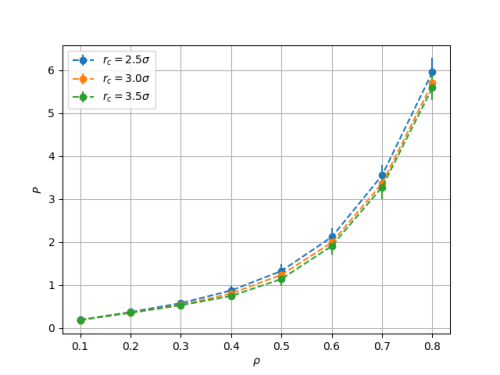
Executando o mesmo esquema, o diagrama é comparado para diferentes valores de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_c} :
Nessa situação (acima do valor crítico de temperatura), o gráfico pressão - densidade mostra sua injetividade, e portanto, a não coexistência de fases (como esperado).
Referências
- ↑ Lennard-Jones, J. E. (1924), "On the Determination of Molecular Fields", Proc. R. Soc. Lond. A, 106 (738): 463–477
- ↑ Daan Frenkel, Berend Smit, "Understanding molecular simulation: from algorithms to applications"
- ↑ David P. Landau, Kurt Binder, "A Guide to Monte Carlo Simulations in Statistical Physics"
- ↑ M Rovere et al (1990) "The gas-liquid transition of the two-dimensional Lennard-Jones fluid". J. Phys.: Condens. Matter 2 7009
- ↑ J.J. Nicolas, K.E. Gubbins, W.B. Streett, and D.J. Tildesley (1979). "Equation of state for the Lennard-Jones fluid". Mol. Phys., 37