Implementação do algoritmo de Neville: mudanças entre as edições
Ir para navegação
Ir para pesquisar
(Criou página com 'Imagem:Neville.png Aqui é descrito um possível mapeamento para fazer o algoritmo de Neville, são descritas as fórmulas do algoritmo de Neville e seu correspondente mapea...') |
Sem resumo de edição |
||
| Linha 5: | Linha 5: | ||
Algoritmo de Neville: | Algoritmo de Neville: | ||
P_{12} = \frac{1}{x_1 - x_2}[(x - x_2)P_{11} - (x - x_1)P_{22}] | :<math>P_{12} = \frac{1}{x_1 - x_2}[(x - x_2)P_{11} - (x - x_1)P_{22}] </math> | ||
Olhando em termos da matriz: | Olhando em termos da matriz: | ||
A_{12} = P_{12} = \frac{1}{X[1] - X[2]}[(x-X[2])A_{11} - (x-X[1])P_{22}]. | :<math>A_{12} = P_{12} = \frac{1}{X[1] - X[2]}[(x-X[2])A_{11} - (x-X[1])P_{22}].</math> | ||
Algoritmo de Neville: | Algoritmo de Neville: | ||
P_{23} = \frac{1}{x_2 - x_3}[(x-x_3)P_{22} - (x - x_2)P_{33}] | :<math>P_{23} = \frac{1}{x_2 - x_3}[(x-x_3)P_{22} - (x - x_2)P_{33}]</math> | ||
Mapeamento: | Mapeamento: | ||
A_{22} = P_{23} = \frac{1}{X[2] - X[3]}[(x-X[3])A_{21} - (x - X[2])A_{31}] | :<math>A_{22} = P_{23} = \frac{1}{X[2] - X[3]}[(x-X[3])A_{21} - (x - X[2])A_{31}]</math> | ||
A. N.: | A. N.: | ||
P_{34} = \frac{1}{x_3 - x_4}[(x-x_4)P_{33} - (x-x_3)P_{44}] | :<math>P_{34} = \frac{1}{x_3 - x_4}[(x-x_4)P_{33} - (x-x_3)P_{44}]</math> | ||
M.: | M.: | ||
A_{32} = P_{34} = \frac{1}{X[3] - X[4]}[(x-X[4])A_{31} - (x-X[3])A_{41}] | :<math>A_{32} = P_{34} = \frac{1}{X[3] - X[4]}[(x-X[4])A_{31} - (x-X[3])A_{41}]</math> | ||
Já é possível notar que | Já é possível notar que | ||
A_{ij} = \frac{1}{X[i] - X[k]}[(x - X[k])A_{i,j-1} - (x - X[i])A_{i+1,j-1}], k=j+i-1 | :<math>A_{ij} = \frac{1}{X[i] - X[k]}[(x - X[k])A_{i,j-1} - (x - X[i])A_{i+1,j-1}], k=j+i-1</math> | ||
Continuando com o A. N.: | Continuando com o A. N.: | ||
P_{123} = \frac{1}{x_1 - x_3}[(x-x_3)P_{12} - (x-x_1)P_{23}] | :<math>P_{123} = \frac{1}{x_1 - x_3}[(x-x_3)P_{12} - (x-x_1)P_{23}]</math> | ||
M.: | M.: | ||
A_{13} = P_{123} = \frac{1}{X[1] - X[3]}[(x-X[3])A_{12} - (x-X[1])A_{22}] | :<math>A_{13} = P_{123} = \frac{1}{X[1] - X[3]}[(x-X[3])A_{12} - (x-X[1])A_{22}]</math> | ||
A. N.: | A. N.: | ||
P_{234} = \frac{1}{x_2-x_4}[(x-x_4)P_{23} - (x-x_3)P_{34}] | :<math>P_{234} = \frac{1}{x_2-x_4}[(x-x_4)P_{23} - (x-x_3)P_{34}]</math> | ||
M.: | M.: | ||
A_{23} = P_{234} = \frac{1}{X[2]-X[4]}[(x-X[4])A_{22} - (x-X[3])A_{32}] | :<math>A_{23} = P_{234} = \frac{1}{X[2]-X[4]}[(x-X[4])A_{22} - (x-X[3])A_{32}]</math> | ||
A. N.: | A. N.: | ||
P_{1234} = \frac{1}{x_1 - x_4}[(x-x_4)P_{123} - (x-x_1)P_{234}] | :<math>P_{1234} = \frac{1}{x_1 - x_4}[(x-x_4)P_{123} - (x-x_1)P_{234}]</math> | ||
M.: | M.: | ||
A_{14} = P_{1234} = \frac{1}{X[1] - X[4]}[(x-X[4])A_{13} - (x-X[1])A_{23}] | :<math>A_{14} = P_{1234} = \frac{1}{X[1] - X[4]}[(x-X[4])A_{13} - (x-X[1])A_{23}]</math> | ||
Chegando finalmente a relação de recorrencia | Chegando finalmente a relação de recorrencia | ||
A_{ij} = \frac{1}{X[i] - X[k]}[(x - X[k])A_{i,j-1} - (x - X[i])A_{i+1,j-1}] | :<math>A_{ij} = \frac{1}{X[i] - X[k]}[(x - X[k])A_{i,j-1} - (x - X[i])A_{i+1,j-1}]</math> | ||
onde | onde | ||
k = j + i | :<math>k = j + i - 1 </math> | ||
No final do processo, o polinômio interpolador é dado por | No final do processo, o polinômio interpolador é dado por | ||
P(x) = A14. | :<math>P(x) = A14.</math> | ||
A leitura dos pontos é dado pelos valores de X e da primeira coluna da matriz A. | A leitura dos pontos é dado pelos valores de X e da primeira coluna da matriz A. | ||
X,Y \rightarrow X[i],A[i][1] | :<math>X,Y \rightarrow X[i],A[i][1]</math> | ||
A ordem do preenchimento é fundamental: | A ordem do preenchimento é fundamental: | ||
j=1;\, i=1,2,3,4 | :<math>j=1;\, i=1,2,3,4 </math> | ||
j=2;\, i=1,2,3 | :<math>j=2;\, i=1,2,3 </math> | ||
j=3;\, i=1,2 | :<math>j=3;\, i=1,2 </math> | ||
j=4;\, i=1 | :<math>j=4;\, i=1 </math> | ||
j=1...N; \, i=1...(N-j+1) | :<math>j=1...N; \, i=1...(N-j+1) </math> | ||
Edição atual tal como às 07h54min de 25 de outubro de 2011
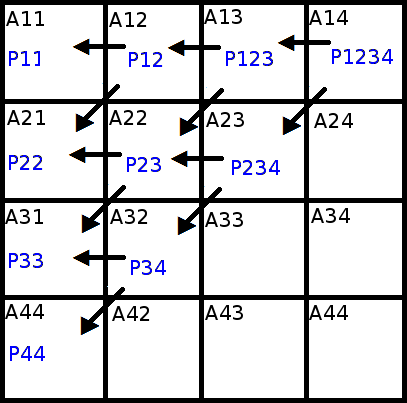
Aqui é descrito um possível mapeamento para fazer o algoritmo de Neville, são descritas as fórmulas do algoritmo de Neville e seu correspondente mapeamento.
Algoritmo de Neville:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{12} = \frac{1}{x_1 - x_2}[(x - x_2)P_{11} - (x - x_1)P_{22}] }
Olhando em termos da matriz:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{12} = P_{12} = \frac{1}{X[1] - X[2]}[(x-X[2])A_{11} - (x-X[1])P_{22}].}
Algoritmo de Neville:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{23} = \frac{1}{x_2 - x_3}[(x-x_3)P_{22} - (x - x_2)P_{33}]}
Mapeamento:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{22} = P_{23} = \frac{1}{X[2] - X[3]}[(x-X[3])A_{21} - (x - X[2])A_{31}]}
A. N.:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{34} = \frac{1}{x_3 - x_4}[(x-x_4)P_{33} - (x-x_3)P_{44}]}
M.:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{32} = P_{34} = \frac{1}{X[3] - X[4]}[(x-X[4])A_{31} - (x-X[3])A_{41}]}
Já é possível notar que
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{ij} = \frac{1}{X[i] - X[k]}[(x - X[k])A_{i,j-1} - (x - X[i])A_{i+1,j-1}], k=j+i-1}
Continuando com o A. N.:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{123} = \frac{1}{x_1 - x_3}[(x-x_3)P_{12} - (x-x_1)P_{23}]}
M.:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{13} = P_{123} = \frac{1}{X[1] - X[3]}[(x-X[3])A_{12} - (x-X[1])A_{22}]}
A. N.:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{234} = \frac{1}{x_2-x_4}[(x-x_4)P_{23} - (x-x_3)P_{34}]}
M.:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{23} = P_{234} = \frac{1}{X[2]-X[4]}[(x-X[4])A_{22} - (x-X[3])A_{32}]}
A. N.:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{1234} = \frac{1}{x_1 - x_4}[(x-x_4)P_{123} - (x-x_1)P_{234}]}
M.:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{14} = P_{1234} = \frac{1}{X[1] - X[4]}[(x-X[4])A_{13} - (x-X[1])A_{23}]}
Chegando finalmente a relação de recorrencia
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{ij} = \frac{1}{X[i] - X[k]}[(x - X[k])A_{i,j-1} - (x - X[i])A_{i+1,j-1}]}
onde
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k = j + i - 1 }
No final do processo, o polinômio interpolador é dado por
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x) = A14.}
A leitura dos pontos é dado pelos valores de X e da primeira coluna da matriz A.
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle X,Y \rightarrow X[i],A[i][1]}
A ordem do preenchimento é fundamental:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=1;\, i=1,2,3,4 }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=2;\, i=1,2,3 }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=3;\, i=1,2 }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=4;\, i=1 }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=1...N; \, i=1...(N-j+1) }