Equação de Klein-Gordon

INTRODUÇÃO

A equação de Klein-Gordon é uma das equações fundamentais na teoria quântica relativística. Ela descreve partículas escalares (partículas sem spin, como os mésons, em seu modelo básico) e é uma extensão relativística da equação de Schrödinger, incorporando a relação de energia relativística de Einstein $E=p^{2}c^{2}+m^{2}c^{4}$. A equação é nomeada em homenagem a Oskar Klein e Walter Gordon, que a formularam independentemente. De maneira geral, a equação pode ser escrita como:

$\left(\Box +{\frac {m^{2}c^{2}}{\hbar ^{2}}}\right)\psi (x,t)=0$

onde $\left(\Box ={\frac {\partial ^{2}}{c^{2}\partial t^{2}}}-\nabla ^{2}\right)$ é chamado operador de d'Alambert.

Abrindo a equação, é obtido:

${\frac {\partial ^{2}\psi }{\partial t^{2}}}=c^{2}\nabla ^{2}\psi -{\frac {m^{2}c^{4}}{\hbar ^{2}}}\psi$

${\frac {\partial ^{2}\psi }{\partial t^{2}}}=c^{2}{\frac {\partial ^{2}\psi }{\partial x^{2}}}-{\frac {m^{2}c^{4}}{\hbar ^{2}}}\psi$ (em uma dimensão)

MÉTODO DAS DIFERENÇAS FINITAS

O método das diferenças finitas é uma técnica numérica amplamente utilizada para resolver EDPs. Ele envolve a discretização das variáveis contínuas (geralmente no tempo ou no espaço), transformando as equações diferenciais em sistemas algébricos que podem ser resolvidos numericamente. Os primeiros passos para utilizar o método é fazer a discretização no tempo e no espaço. Para uma equação no tempo você discretiza o tempo em intervalos $\Delta t$ criando uma sequência de pontos $t_{n}=n\Delta t$. Para uma equação no espaço você discretiza o espaço em intervalos $\Delta x$ criando uma sequência de pontos $x_{i}=i\Delta x$. Depois de discretizar o espaço e o tempo, as derivadas contínuas são aproximadas por diferenças finitas. Isso envolve substituir as derivadas por aproximações baseadas nos valores de uma função nos pontos discretos:

${\frac {\partial u}{\partial t}}\approx {\frac {u_{i}^{n+1}-u_{i}^{n}}{\Delta t}}$ e ${\frac {\partial ^{2}u}{\partial t^{2}}}\approx {\frac {u_{i}^{n+1}-2u_{i}^{n}+u_{i}^{n-1}}{(\Delta t)^{2}}}$ para o tempo.

${\frac {\partial u}{\partial x}}\approx {\frac {u_{i+1}^{n}-u_{i}^{n}}{\Delta x}}e{\frac {\partial ^{2}u}{\partial x^{2}}}\approx {\frac {u_{i+1}^{n}-2u_{i}^{n}+u_{i-1}^{n}}{(\Delta x)^{2}}}$ para o espaço.

Na equação de Klein-Gordon, escrevemos desta o método das diferenças finitas:

${\frac {\partial ^{2}\psi (x,t)}{\partial t^{2}}}\approx {\frac {\psi (x,t+\Delta t)-2\psi (x,t)+\psi (x,t-\Delta t)}{(\Delta t)^{2}}}$

${\frac {\partial ^{2}\psi (x,t)}{\partial x^{2}}}\approx {\frac {\psi (x+\Delta x,t)-2\psi (x,t)+\psi (x-\Delta x,t)}{(\Delta x)^{2}}}$

ou seja:

${\frac {\psi (x,t+\Delta t)-2\psi (x,t)+\psi (x,t-\Delta t)}{(\Delta t)^{2}}}=c^{2}{\frac {\psi (x+\Delta x,t)-2\psi (x,t)+\psi (x,t-\Delta t)}{(\Delta x)^{2}}}-{\frac {m^{2}c^{4}}{\hbar ^{2}}}\psi$

isso nos leva a equação final:

$\psi (x,t+\Delta t)-2\psi (x,t)+\psi (x,t-\Delta t)={\frac {c^{2}\Delta t^{2}}{\Delta x^{2}}}\psi (x+\Delta x,t)-2\psi (x,t)+\psi (x,t-\Delta ,t)-{\frac {m^{2}c^{4}\Delta t^{2}}{\hbar ^{2}}}\psi$

chamarei $\alpha ={\frac {c\Delta t}{\Delta x}}$ e $\beta ={\frac {mc^{2}\Delta t}{\hbar }}$

portanto, $\psi (x,t+\Delta t)-2\psi (x,t)+\psi (x,t-\Delta t)=\alpha ^{2}\psi (x+\Delta x,t)-2\psi (x,t)+\psi (x,t-\Delta t)-\beta ^{2}\psi$

ou, mais usualmente: $\psi _{i}^{n+1}=2\psi _{i}^{n}-\psi _{i}^{n-1}+\alpha ^{2}(\psi _{i+1}^{n}-2\psi _{i}^{n}+\psi _{i-1}^{n})-\beta ^{2}\psi$

CRITÉRIO DE ESTABILIDADE

A Forma Contínua e Eiscretização da equação de Klein-Gordon contínua é: ${\frac {\partial ^{2}\psi }{\partial t^{2}}}=c^{2}{\frac {\partial ^{2}\psi }{\partial x^{2}}}-{\frac {m^{2}c^{4}}{\hbar ^{2}}}\psi .$

A forma discreta, usando diferenças finitas centralizadas no tempo e no espaço, é: $\psi _{i}^{n+1}=2\psi _{i}^{n}-\psi _{i}^{n-1}+{\frac {c^{2}\Delta t^{2}}{\Delta x^{2}}}(\psi _{i+1}^{n}-2\psi _{i}^{n}+\psi _{i-1}^{n})-{\frac {m^{2}c^{4}\Delta t^{2}}{\hbar ^{2}}}\psi _{i}^{n}.$ Aqui, definimos os coeficientes: $\alpha ={\frac {c\Delta t}{\Delta x}},\quad \beta ={\frac {mc^{2}\Delta t}{\hbar }}.$

Suposição de Solução Harmônica: Substituímos uma solução da forma: $\psi _{i}^{n}=G^{n}e^{ikx_{i}},$ onde:

 na equação: $G^{n+1}e^{ikx_{i}}=2G^{n}e^{ikx_{i}}-G^{n-1}e^{ikx_{i}}+\alpha ^{2}G^{n}\left(e^{ikx_{i+1}}-2e^{ikx_{i}}+e^{ikx_{i-1}}\right)-\beta ^{2}G^{n}e^{ikx_{i}}.$

Simplificação:

Como $e^{ikx_{i+1}}=e^{ikx_{i}}e^{ik\Delta x}$ e $e^{ikx_{i-1}}=e^{ikx_{i}}e^{-ik\Delta x}$, o termo centralizado se torna: $e^{ikx_{i+1}}-2e^{ikx_{i}}+e^{ikx_{i-1}}=e^{ikx_{i}}\left(e^{ik\Delta x}-2+e^{-ik\Delta x}\right).$ Usando $e^{ik\Delta x}+e^{-ik\Delta x}=2\cos(k\Delta x)$, temos: $e^{ikx_{i+1}}-2e^{ikx_{i}}+e^{ikx_{i-1}}=e^{ikx_{i}}\left(-2+2\cos(k\Delta x)\right).$ Substituímos isso na equação e cancelamos o fator $e^{ikx_{i}}$, que nunca é zero: $G^{n+1}=2G^{n}-G^{n-1}-\alpha ^{2}(2-2\cos(k\Delta x))G^{n}-\beta ^{2}G^{n}.$

Simplificando mais, obtemos: $G^{n+1}=(2-\alpha ^{2}(2-2\cos(k\Delta x))-\beta ^{2})G^{n}-G^{n-1}.$

Equação Característica: Assumimos uma solução da forma $G^{n}=G^{n}$ e obtemos uma equação quadrática para $G$: $G^{2}-G\left(2-\alpha ^{2}(2-2\cos(k\Delta x))-\beta ^{2}\right)+1=0.$

Condição de Estabilidade: Para estabilidade, as raízes de $G$ devem satisfazer $|G|\leq 1$. Isso leva ao critério: $\alpha \leq 1,\quad {\text{ou seja,}}\quad {\frac {c\Delta t}{\Delta x}}\leq 1.$

Conclusão Matemática A condição $\alpha \leq 1$ garante que os termos oscilatórios na solução não crescem exponencialmente. Essa análise também mostra que:

Quanto menor o passo de tempo $\Delta t$, mais precisa e estável é a solução. A relação entre os passos de tempo e espaço é crucial: aumentar muito $\Delta t$ sem ajustar $\Delta x$ pode levar à instabilidade.

C.C e C.I

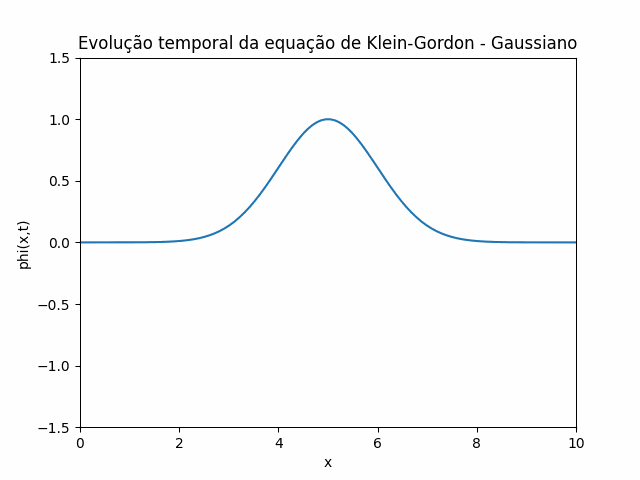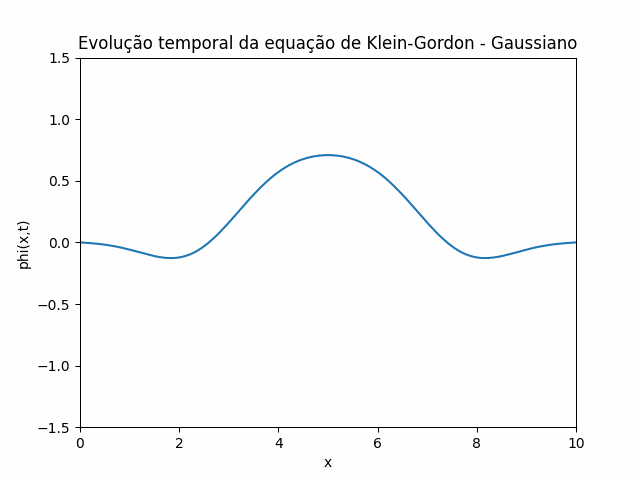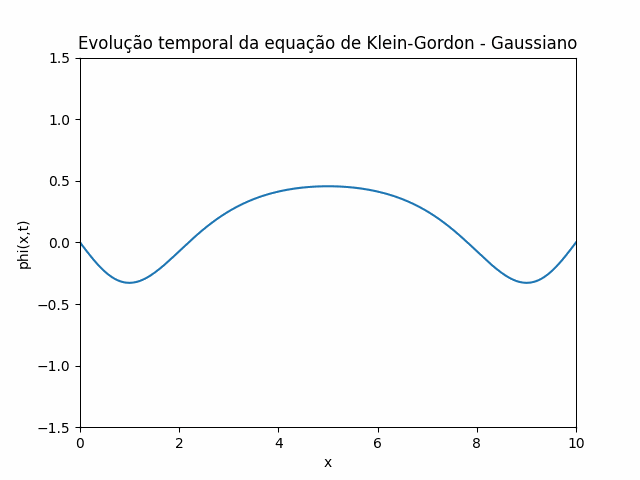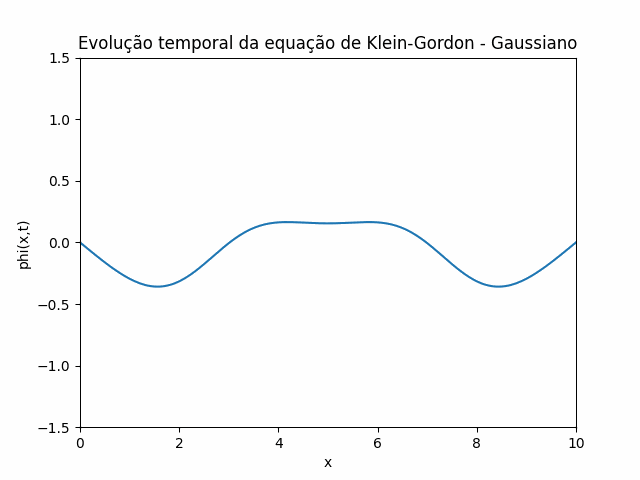
Condições iniciais e condições de contorno são fundamentais para a resolução da equação, já que elas ditam o comportamento da função oa longo do tempo e ao longo do espaço, para plotar a evolução temporal, utilizarei as seguintes condilções iniciais e de contorno:

$\psi (x,0)=Ae^{-{\frac {x-x_{0}}{2\sigma ^{2}}}}$ que define um pulso gaussiano como condição inicial.

e ${\frac {\partial \psi (x,0)}{\partial t}}=0$ que define que, no instante de tempo t=0, a função não possui velocidade inicial, o que implica que o pulso está parado inicialmente e sua evolução se deve pela propagação de flutuações espaciais.

Nesta condição, A é a altura do pulso, $x_{0}$ é a posição central do pulso e $\sigma$ é a largura do pulso.

Utilizarei também as condições de contorno em que $\psi (0,t)=0$ e $\psi (L,t)=0$ o que garante que a função 'morra' nas pontas.

Utilizando estas condições iniciais e condições de contorno, foi feito um gif que mostra a evolução temporal da equação de Klein-Gordon utilizando o método das diferenças finitas: