Dinâmica Molecular - Método das Caixas: mudanças entre as edições
Sem resumo de edição |
|||
| (24 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
Neste estudo, foi investigado o desempenho e a precisão de simulações de dinâmica molecular utilizando o potencial de Lennard-Jones. Foram comparados dois métodos computacionais: o método tradicional, que calcula as interações e as forças entre todos os pares de partículas que estão | Neste estudo, foi investigado o desempenho e a precisão de simulações de dinâmica molecular utilizando o potencial de Lennard-Jones. Foram comparados dois métodos computacionais: o método tradicional, que calcula as interações e as forças entre todos os pares de partículas que estão contidas em uma caixa bidimensional, e o método baseado em células, que otimiza os cálculos ao limitar o alcance das interações às células vizinhas. Ambos os métodos foram implementados em duas dimensões com condições periódicas de contorno (PBC). | ||
Avaliamos o desempenho dos métodos analisando o tempo de execução em função do número de partículas. Os resultados mostram que o método baseado em células reduz significativamente o tempo de execução para sistemas grandes, demonstrando sua eficiência e reprodutibilidade. A conservação da energia, incluindo as energias cinética, potencial e total, foi validada para ambos os métodos ao longo do tempo, mostrando que o método mantém o significado físico da simulação. | Avaliamos o desempenho dos métodos analisando o tempo de execução em função do número de partículas. Os resultados mostram que o método baseado em células reduz significativamente o tempo de execução para sistemas grandes, demonstrando sua eficiência e reprodutibilidade. A conservação da energia, incluindo as energias cinética, potencial e total, foi validada para ambos os métodos ao longo do tempo, mostrando que o método mantém o significado físico da simulação. | ||
| Linha 6: | Linha 6: | ||
Inicialmente, o problema do tempo perdido em simulações normais de dinâmica molecular está relacionado ao crescimento do número de cálculos necessários conforme aumenta o número de partículas no sistema. Essa questão tem um impacto direto na eficiência e no tempo de execução de simulações, já que para cada par de partículas, é necessário calcular a distância relativa, aplicar o potencial desejado, e determinar a força resultante. Portanto, a parte temporal mais custosa na simulação está no calculo de forças, e na determinação da distância de cada partícula. | Inicialmente, o problema do tempo perdido em simulações normais de dinâmica molecular está relacionado ao crescimento do número de cálculos necessários conforme aumenta o número de partículas no sistema. Essa questão tem um impacto direto na eficiência e no tempo de execução de simulações, já que para cada par de partículas, é necessário calcular a distância relativa, aplicar o potencial desejado, e determinar a força resultante. Portanto, a parte temporal mais custosa na simulação está no calculo de forças, e na determinação da distância de cada partícula. | ||
Para N partículas, temos <math>N=\frac{N(N-1)}{2}</math> pares de interação, e se tivermos um sistema com um número significativamente grande de partículas, o problema terá uma complexidade de <math> O(N^2) </math> . Essa dependência quadrática do número de partículas torna as simulações normais impraticáveis para sistemas com grande número de partículas <math> (N>10^5)</math> já que o tempo de execução cresce rapidamente. Além disso, são necessários recursos computacionais elevados para simulações maiores pois a demanda por processamento irá crescer cada vez mais, exigindo computadores mais potentes ou tempo de execução excessivo. | Para N partículas, temos <math>N=\frac{N(N-1)}{2}</math> pares de interação, e se tivermos um sistema com um número significativamente grande de partículas, o problema terá uma complexidade de <math> O(N^2) </math> . Essa dependência quadrática do número de partículas torna as simulações normais impraticáveis em computadores comuns para sistemas com grande número de partículas <math> (N>10^5)</math> já que o tempo de execução cresce rapidamente. Além disso, são necessários recursos computacionais elevados para simulações maiores pois a demanda por processamento irá crescer cada vez mais, exigindo computadores mais potentes ou tempo de execução excessivo. | ||
Portanto há a necessidade de diminuir a ordem para que o tempo seja menos custoso nas simulações. Para isso, existem diversos algorítmos e métodos que podem ser uteis, como o Método das Caixas, o Algorítmo de Edwald e PME, o Método de Multipolos Hierárquicos, e a Implementação Paralela. O objetivo deste trabalho é desenvolver o Método das Caixas, ou Método das Células, para a otimização das simulações. | Portanto há a necessidade de diminuir a ordem para que o tempo seja menos custoso nas simulações. Para isso, existem diversos algorítmos e métodos que podem ser uteis, como o Método das Caixas, o Algorítmo de Edwald e PME, o Método de Multipolos Hierárquicos, e a Implementação Paralela. O objetivo deste trabalho é desenvolver o Método das Caixas, ou Método das Células, para a otimização das simulações. | ||
== CONDIÇÕES PERIÓDICAS DE CONTORNO == | == CONDIÇÕES PERIÓDICAS DE CONTORNO == | ||
As condições periódicas de contorno (PBC) são utilizadas para simular sistemas finitos que se comportam como se fossem muito grandes, eliminando os efeitos artificiais de borda. Dessa maneira, em uma simulação com PBC, o sistema principal é replicado em todas as direções, formando uma grade infinita de caixas idênticas. Quando uma partícula cruza o limite de uma caixa, ela reaparece automaticamente pelo lado oposto, mantendo uma continuidade espacial. Esse mecanismo permite que partículas interajam não apenas dentro da caixa principal, mas também com as imagens de partículas em caixas vizinhas, criando um ambiente mais realista e aproximado às condições de sistemas macroscópicos. | As condições periódicas de contorno (PBC) são utilizadas para simular sistemas finitos que se comportam como se fossem muito grandes, eliminando os efeitos artificiais de borda. Dessa maneira, em uma simulação com PBC, o sistema principal é replicado em todas as direções, formando uma grade infinita de caixas idênticas. Quando uma partícula cruza o limite de uma caixa, ela reaparece automaticamente pelo lado oposto, mantendo uma continuidade espacial. Esse mecanismo permite que partículas interajam não apenas dentro da caixa principal, mas também com as imagens de partículas em caixas vizinhas, criando um ambiente mais realista e aproximado às condições de sistemas macroscópicos. <ref> https://arxiv.org/pdf/2001.07089 </ref> | ||
Além disso, as PBC | Além disso, as PBC são necessárias para o cálculo de distâncias entre partículas, considerando a menor distância possível entre elas, mesmo que estejam em caixas adjacentes. Isso é feito ajustando as coordenadas das partículas para a caixa principal, garantindo interações corretas. Esse ajuste reduz a necessidade de processar bordas artificiais e preserva a conservação de energia e momento. Com isso, as PBC se tornam fundamentais em simulações de líquidos, gases e sólidos, permitindo representar adequadamente sistemas que, na realidade, são infinitos ou muito maiores que o volume modelado. | ||
[[Arquivo:Limiteperiodicite.svg.png]] | |||
== EXPLICANDO O MÉTODO == | == EXPLICANDO O MÉTODO == | ||
O princípio básico do método das caixas é diminuir o número de cálculos de forças de interação entre as partículas, já que em uma simulação normal é computado a interação de cada uma delas com todas as outras. Porém, como as forças de interação são geralmente de curto alcance, basta calculá-las entre cada partícula e seus vizinhos mais próximos. | O princípio básico do método das caixas é diminuir o número de cálculos de forças de interação entre as partículas, já que em uma simulação normal é computado a interação de cada uma delas com todas as outras. Porém, como as forças de interação são geralmente de curto alcance, basta calculá-las entre cada partícula e seus vizinhos mais próximos. | ||
Para isso, podemos dividir o espaço da caixa em caixinhas quadradas de lado L que deve ser pelo menos igual ao raio de corte, que é a distância máxima em que as partículas ainda podem interagir. Dessa maneira, cada caixa pode ser identificada com um número correspondente, e cada caixa está associada também a uma lista de números que correspondem as partículas cujos centros ainda se encontram na caixa. As forças de interações de cada partícula será calculada apenas com as partículas da mesma célula e das células vizinhas. | Para isso, podemos dividir o espaço da caixa em caixinhas quadradas de lado L que deve ser pelo menos igual ao raio de corte, que é a distância máxima em que as partículas ainda podem interagir. Dessa maneira, cada caixa pode ser identificada com um número correspondente, e cada caixa está associada também a uma lista de números que correspondem as partículas cujos centros ainda se encontram na caixa. As forças de interações de cada partícula será calculada apenas com as partículas da mesma célula e das células vizinhas. <ref> Métodos Computacionais da Física - Claudio Scherer </ref> | ||
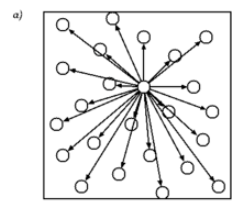
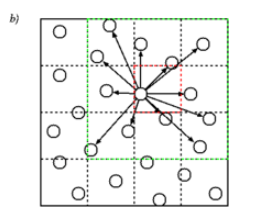
Na figura abaixo, em a) temos a interação de cada par de partícula, entre todas as partículas, e em b) dividimos o espaço em caixas que tem pelo menos um lado igual ao raio de corte do potencial, assim, computamos as interações entre as partículas na mesma caixa e em caixas vizinhas. | Na figura abaixo, em a) temos a interação de cada par de partícula, entre todas as partículas, e em b) dividimos o espaço em caixas que tem pelo menos um lado igual ao raio de corte do potencial, assim, computamos as interações entre as partículas na mesma caixa e em caixas vizinhas. | ||
[[Arquivo: | [[Arquivo:hhh.png]] | ||
[[Arquivo:Ggg.png]] | |||
(WIKIPEDIA CONTRIBUTORS, 2022) | (WIKIPEDIA CONTRIBUTORS, 2022) <ref> https://en.wikipedia.org/wiki/Cell_lists WIKIPEDIA CONTRIBUTORS. Cell lists. </ref> | ||
== RESULTADOS == | == RESULTADOS == | ||
| Linha 29: | Linha 32: | ||
Abaixo, encontra-se o gráfico de energia potencial, cinética e total, feito utilizando a simulação tradicional. | Abaixo, encontra-se o gráfico de energia potencial, cinética e total, feito utilizando a simulação tradicional, todos foram utilizados a mesma condição inicial e a mesma seed. | ||
[[Arquivo:dads.png]] | [[Arquivo:dads.png]] | ||
| Linha 35: | Linha 38: | ||
[[Arquivo:lll.png]] | [[Arquivo:lll.png]] | ||
Abaixo, encontram-se os mesmos gráficos acima, porém superpostos para fins de comparação. | |||
[[Arquivo:Coma.png]] | |||
Portanto, é notório que a energia total permanece constante com o tempo, o que mostra que o método funciona e não dá resultados diferentes do esperado. | Portanto, é notório que a energia total permanece constante com o tempo, o que mostra que o método funciona e não dá resultados diferentes do esperado. | ||
| Linha 46: | Linha 53: | ||
Abaixo, encontra-se o gráfico de Tempo de execução x Número de partículas. Assim, é visto que o método das caixas tem um tempo de execução bem menor que o método tradicional, concluindo que é um método simples e que deve ser utilizado em simulações computacionais de alto custo a fim de otimizar o tempo gasto. | Abaixo, encontra-se o gráfico de Tempo de execução x Número de partículas. Assim, é visto que o método das caixas tem um tempo de execução bem menor que o método tradicional, concluindo que é um método simples e que deve ser utilizado em simulações computacionais de alto custo a fim de otimizar o tempo gasto. | ||
[[Arquivo: | [[Arquivo:nomer.png]] | ||
[[Arquivo:ordem.png]] | |||
== CONCLUSÃO == | == CONCLUSÃO == | ||
O estudo conduzido sobre a aplicação do método das caixas em simulações de dinâmica molecular demonstra avanços significativos em termos de eficiência computacional, sem comprometer a precisão dos resultados físicos. Ao reduzir a complexidade computacional de | O estudo conduzido sobre a aplicação do método das caixas em simulações de dinâmica molecular demonstra avanços significativos em termos de eficiência computacional, sem comprometer a precisão dos resultados físicos. Ao reduzir a complexidade computacional de <math>O(N^2)</math> para <math>O(N)</math>, o método se mostra essencial para a simulação de sistemas com grande quantidade de partículas, viabilizando análises que seriam impraticáveis com o método tradicional. As condições periódicas de contorno (PBC) desempenham um papel crucial ao eliminar efeitos de borda, garantindo que o ambiente simulado seja realista e consistente com sistemas macroscópicos. A conservação das energias cinética, potencial e total, evidenciada nos resultados, comprova que o método das caixas não introduz distorções nos resultados físicos esperados. Além disso, a redução expressiva do tempo de execução, conforme ilustrado pelos gráficos, reforça a superioridade do método na otimização de recursos computacionais. | ||
Portanto, o método das caixas é uma ferramenta poderosa para otimizar simulações de dinâmica molecular, especialmente em sistemas com interações de curto alcance. Ele não apenas melhora a escalabilidade das simulações, mas também preserva a integridade dos resultados físicos, mostrando-se indispensável para estudos computacionais de grande escala em física, química e biologia. | Portanto, o método das caixas é uma ferramenta poderosa para otimizar simulações de dinâmica molecular, especialmente em sistemas com interações de curto alcance. Ele não apenas melhora a escalabilidade das simulações, mas também preserva a integridade dos resultados físicos, mostrando-se indispensável para estudos computacionais de grande escala em física, química e biologia. | ||
== REFERÊNCIAS == | == REFERÊNCIAS == | ||
Understanding Molecular Simulation - Daan Frenkel and Berend Smit | [https://www.eng.uc.edu/~beaucag/Classes/AdvancedMaterialsThermodynamics/Books/%5BComputational%20science%20(San%20Diego,%20Calif.)%5D%20Daan%20Frenkel_%20Berend%20Smit%20-%20Understanding%20molecular%20simulation%20_%20from%20algorithms%20to%20applications%20(2002,%20Academic%20Press%20)%20-%20libgen.lc.pdf Understanding Molecular Simulation - Daan Frenkel and Berend Smit] | ||
WIKIPEDIA CONTRIBUTORS. Cell lists. | [https://en.wikipedia.org/wiki/Cell_lists WIKIPEDIA CONTRIBUTORS. Cell lists.] | ||
Métodos Computacionais da Física - Claudio Scherer | Métodos Computacionais da Física - Claudio Scherer | ||
Edição atual tal como às 15h30min de 11 de dezembro de 2024
Neste estudo, foi investigado o desempenho e a precisão de simulações de dinâmica molecular utilizando o potencial de Lennard-Jones. Foram comparados dois métodos computacionais: o método tradicional, que calcula as interações e as forças entre todos os pares de partículas que estão contidas em uma caixa bidimensional, e o método baseado em células, que otimiza os cálculos ao limitar o alcance das interações às células vizinhas. Ambos os métodos foram implementados em duas dimensões com condições periódicas de contorno (PBC).
Avaliamos o desempenho dos métodos analisando o tempo de execução em função do número de partículas. Os resultados mostram que o método baseado em células reduz significativamente o tempo de execução para sistemas grandes, demonstrando sua eficiência e reprodutibilidade. A conservação da energia, incluindo as energias cinética, potencial e total, foi validada para ambos os métodos ao longo do tempo, mostrando que o método mantém o significado físico da simulação.
INTRODUÇÃO
Inicialmente, o problema do tempo perdido em simulações normais de dinâmica molecular está relacionado ao crescimento do número de cálculos necessários conforme aumenta o número de partículas no sistema. Essa questão tem um impacto direto na eficiência e no tempo de execução de simulações, já que para cada par de partículas, é necessário calcular a distância relativa, aplicar o potencial desejado, e determinar a força resultante. Portanto, a parte temporal mais custosa na simulação está no calculo de forças, e na determinação da distância de cada partícula.
Para N partículas, temos pares de interação, e se tivermos um sistema com um número significativamente grande de partículas, o problema terá uma complexidade de . Essa dependência quadrática do número de partículas torna as simulações normais impraticáveis em computadores comuns para sistemas com grande número de partículas já que o tempo de execução cresce rapidamente. Além disso, são necessários recursos computacionais elevados para simulações maiores pois a demanda por processamento irá crescer cada vez mais, exigindo computadores mais potentes ou tempo de execução excessivo.
Portanto há a necessidade de diminuir a ordem para que o tempo seja menos custoso nas simulações. Para isso, existem diversos algorítmos e métodos que podem ser uteis, como o Método das Caixas, o Algorítmo de Edwald e PME, o Método de Multipolos Hierárquicos, e a Implementação Paralela. O objetivo deste trabalho é desenvolver o Método das Caixas, ou Método das Células, para a otimização das simulações.
CONDIÇÕES PERIÓDICAS DE CONTORNO
As condições periódicas de contorno (PBC) são utilizadas para simular sistemas finitos que se comportam como se fossem muito grandes, eliminando os efeitos artificiais de borda. Dessa maneira, em uma simulação com PBC, o sistema principal é replicado em todas as direções, formando uma grade infinita de caixas idênticas. Quando uma partícula cruza o limite de uma caixa, ela reaparece automaticamente pelo lado oposto, mantendo uma continuidade espacial. Esse mecanismo permite que partículas interajam não apenas dentro da caixa principal, mas também com as imagens de partículas em caixas vizinhas, criando um ambiente mais realista e aproximado às condições de sistemas macroscópicos. [1]
Além disso, as PBC são necessárias para o cálculo de distâncias entre partículas, considerando a menor distância possível entre elas, mesmo que estejam em caixas adjacentes. Isso é feito ajustando as coordenadas das partículas para a caixa principal, garantindo interações corretas. Esse ajuste reduz a necessidade de processar bordas artificiais e preserva a conservação de energia e momento. Com isso, as PBC se tornam fundamentais em simulações de líquidos, gases e sólidos, permitindo representar adequadamente sistemas que, na realidade, são infinitos ou muito maiores que o volume modelado.
EXPLICANDO O MÉTODO
O princípio básico do método das caixas é diminuir o número de cálculos de forças de interação entre as partículas, já que em uma simulação normal é computado a interação de cada uma delas com todas as outras. Porém, como as forças de interação são geralmente de curto alcance, basta calculá-las entre cada partícula e seus vizinhos mais próximos. Para isso, podemos dividir o espaço da caixa em caixinhas quadradas de lado L que deve ser pelo menos igual ao raio de corte, que é a distância máxima em que as partículas ainda podem interagir. Dessa maneira, cada caixa pode ser identificada com um número correspondente, e cada caixa está associada também a uma lista de números que correspondem as partículas cujos centros ainda se encontram na caixa. As forças de interações de cada partícula será calculada apenas com as partículas da mesma célula e das células vizinhas. [2]
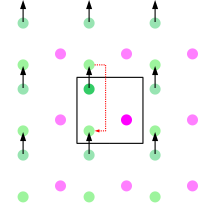
Na figura abaixo, em a) temos a interação de cada par de partícula, entre todas as partículas, e em b) dividimos o espaço em caixas que tem pelo menos um lado igual ao raio de corte do potencial, assim, computamos as interações entre as partículas na mesma caixa e em caixas vizinhas.
(WIKIPEDIA CONTRIBUTORS, 2022) [3]
RESULTADOS
A técnica das caixas em dinâmica molecular é usada para melhorar a eficiência computacional ao calcular interações entre partículas em sistemas com muitas partículas. Dividindo o espaço simulado em células menores, as partículas interagem apenas com vizinhas dentro de um raio de corte, reduzindo a complexidade computacional de para , o que permite realizar simulações mais rápidas sem comprometer a precisão das medidas físicas, como energia potencial e forças entre partículas, que permanecem consistentes com o potencial de Lennard-Jones. Além disso, quando combinada com condições periódicas de contorno, a técnica elimina efeitos de borda indesejados. Portanto, serão analisadas medidas de energia, tanto com simulações tradicionais quanto com simulações que utilizam o método das caixas para comprovar não só a eficácia do método, mas também que o tempo de simulação é bem menor.
Abaixo, encontra-se o gráfico de energia potencial, cinética e total, feito utilizando a simulação tradicional, todos foram utilizados a mesma condição inicial e a mesma seed.

Abaixo, encontra-se o gráfico de energia potencial, cinética e total, feito utilizando o método das caixas.
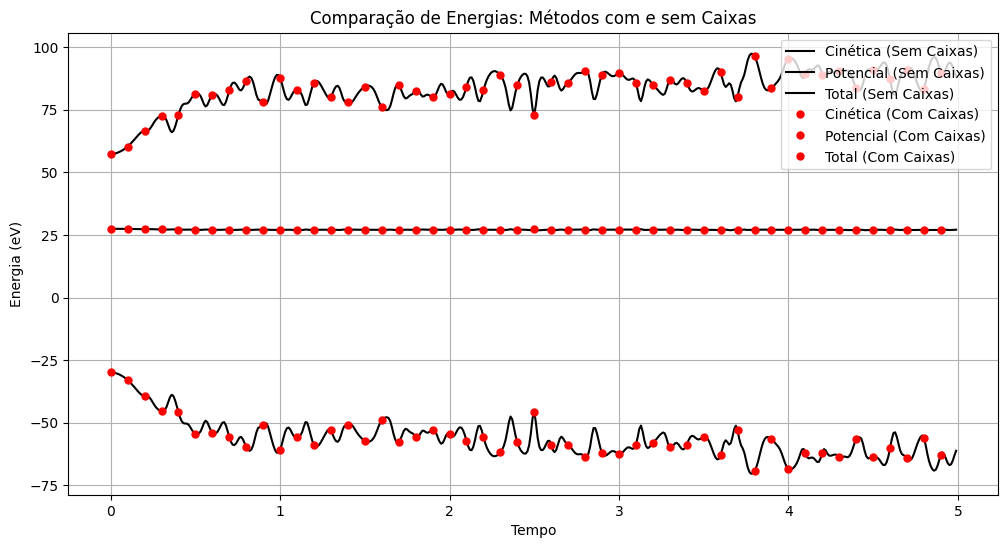
Abaixo, encontram-se os mesmos gráficos acima, porém superpostos para fins de comparação.
Portanto, é notório que a energia total permanece constante com o tempo, o que mostra que o método funciona e não dá resultados diferentes do esperado.
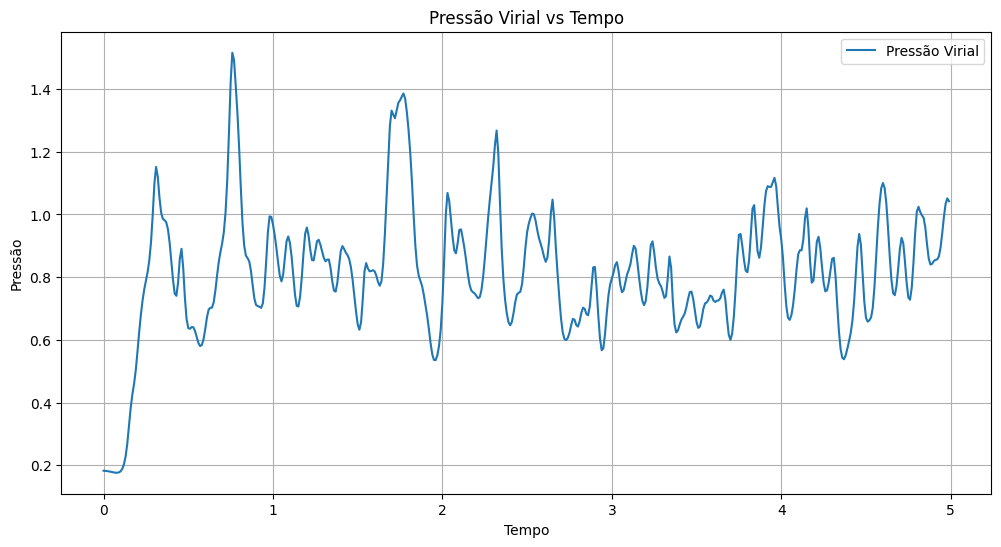
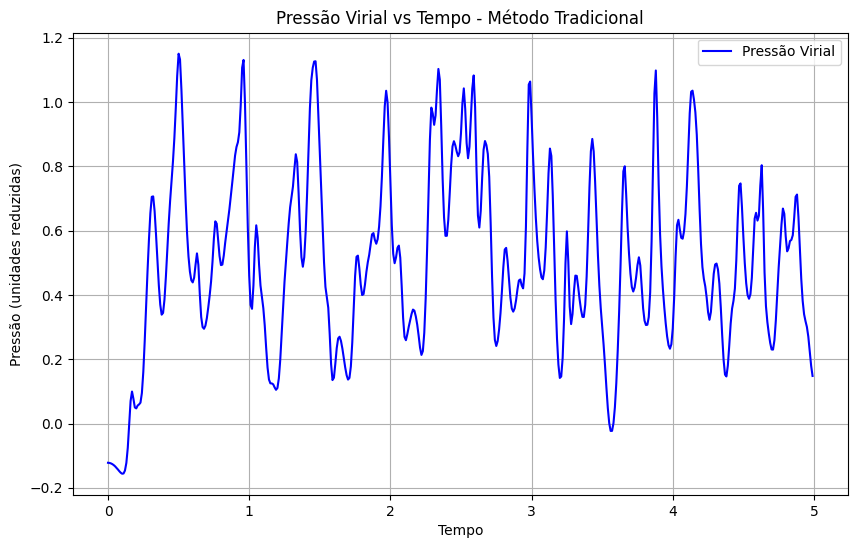
Por fim, nas figuras abaixo está o gráfico da pressão do sistema, calculada utilizando o método das caixas e o método tradicional. É notório que os resultados permanecem semelhantes e, portanto, a veracidade do método das caixas ainda é sustentável.
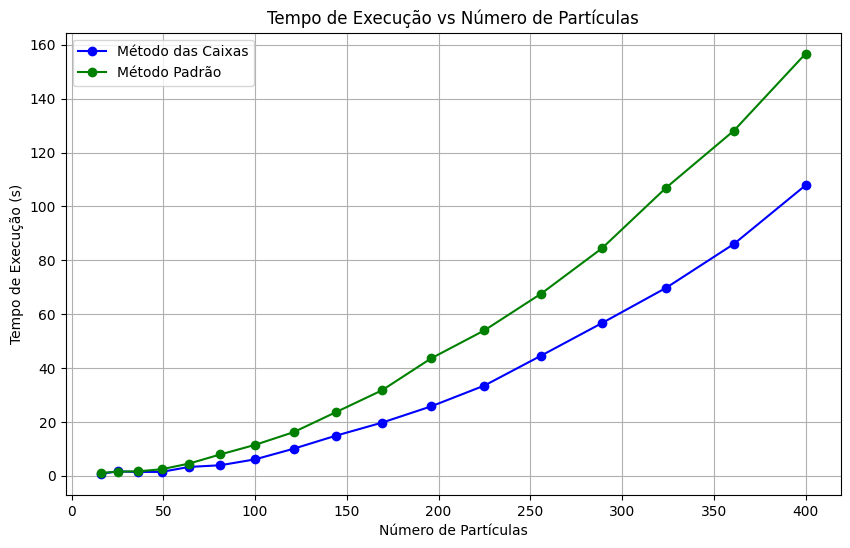
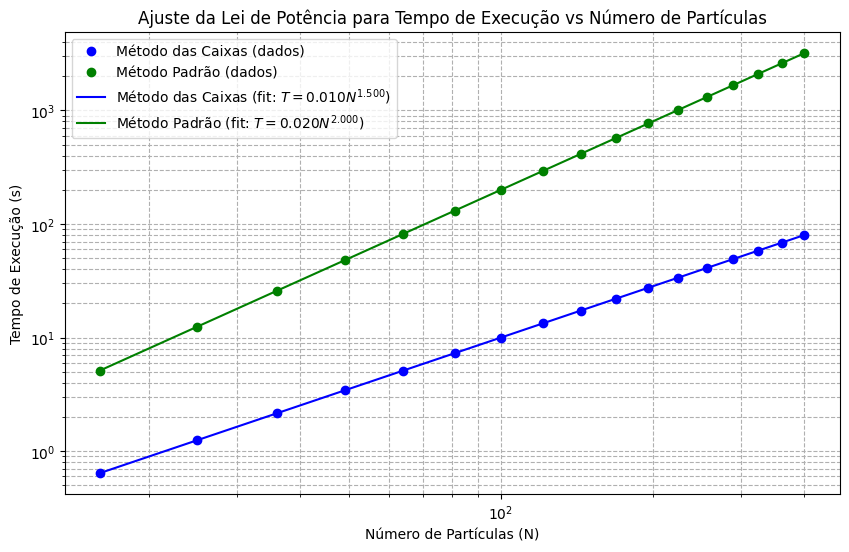
Abaixo, encontra-se o gráfico de Tempo de execução x Número de partículas. Assim, é visto que o método das caixas tem um tempo de execução bem menor que o método tradicional, concluindo que é um método simples e que deve ser utilizado em simulações computacionais de alto custo a fim de otimizar o tempo gasto.
CONCLUSÃO
O estudo conduzido sobre a aplicação do método das caixas em simulações de dinâmica molecular demonstra avanços significativos em termos de eficiência computacional, sem comprometer a precisão dos resultados físicos. Ao reduzir a complexidade computacional de para , o método se mostra essencial para a simulação de sistemas com grande quantidade de partículas, viabilizando análises que seriam impraticáveis com o método tradicional. As condições periódicas de contorno (PBC) desempenham um papel crucial ao eliminar efeitos de borda, garantindo que o ambiente simulado seja realista e consistente com sistemas macroscópicos. A conservação das energias cinética, potencial e total, evidenciada nos resultados, comprova que o método das caixas não introduz distorções nos resultados físicos esperados. Além disso, a redução expressiva do tempo de execução, conforme ilustrado pelos gráficos, reforça a superioridade do método na otimização de recursos computacionais. Portanto, o método das caixas é uma ferramenta poderosa para otimizar simulações de dinâmica molecular, especialmente em sistemas com interações de curto alcance. Ele não apenas melhora a escalabilidade das simulações, mas também preserva a integridade dos resultados físicos, mostrando-se indispensável para estudos computacionais de grande escala em física, química e biologia.
REFERÊNCIAS
Understanding Molecular Simulation - Daan Frenkel and Berend Smit
WIKIPEDIA CONTRIBUTORS. Cell lists.
Métodos Computacionais da Física - Claudio Scherer
- ↑ https://arxiv.org/pdf/2001.07089
- ↑ Métodos Computacionais da Física - Claudio Scherer
- ↑ https://en.wikipedia.org/wiki/Cell_lists WIKIPEDIA CONTRIBUTORS. Cell lists.