Termostato de Andersen: mudanças entre as edições
| Linha 60: | Linha 60: | ||
== RESULTADOS == | == RESULTADOS == | ||
Para verificar se o termostato está corretamente simulando o ensemble canônico, foram escolhidas 3 temperaturas diferentes. Para cada uma delas, foi simulado n=108 partículas, com densidade p=0.8442, nu=0.5, dt=0.001 e número de passos N=50.000. | |||
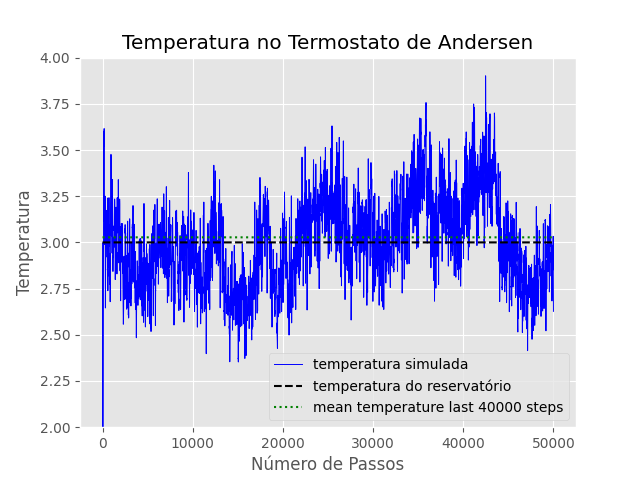
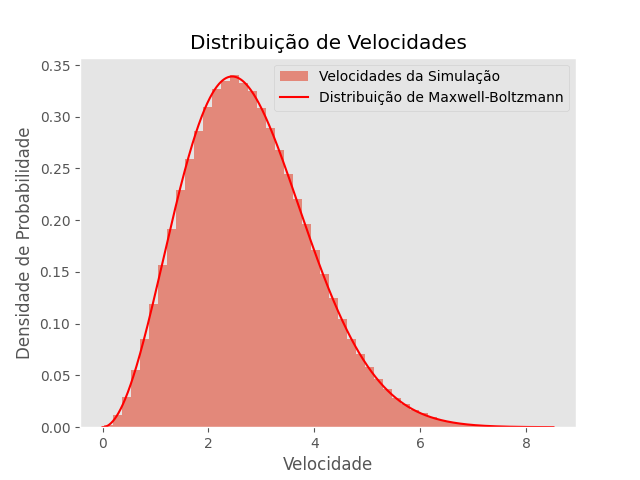
T=1 | São mostradas abaixo a série temporal para cada uma das temperaturas. Para checar de forma mais consistente se o sistema no equilíbrio realmente corresponde ao ensemble canônico, foi comparada a curva teórica da distribuição de Maxwell-Boltzmann para a temperatura correspondente, com um histograma das velocidades em todas as dimensões obtidas nos últimos 40.000 passos (os primeiros 10.000 passos é o transiente para o equilíbrio). | ||
Além disso, foi calculada a média e o desvio-padrão para cada uma dessas medidas. | |||
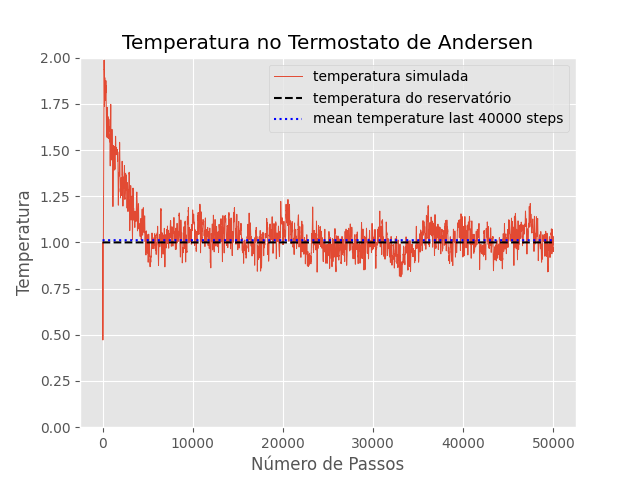
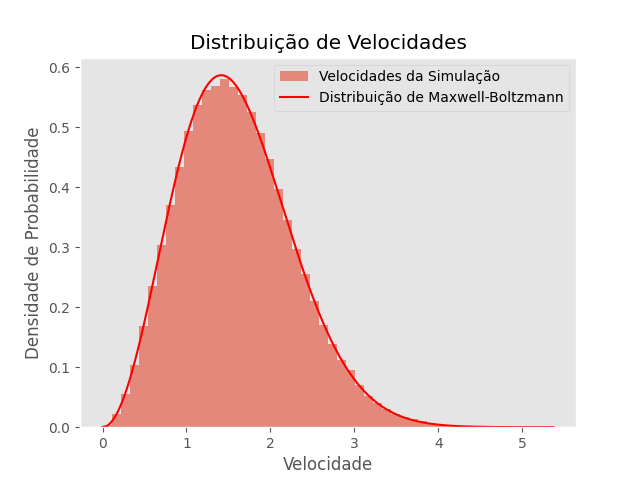
=== T=1 === | |||
<math>\mu = 1.011</math> | <math>\mu = 1.011</math> | ||
<math>\sigma = 0.067</math> | <math>\sigma = 0.067</math> | ||
| Linha 70: | Linha 73: | ||
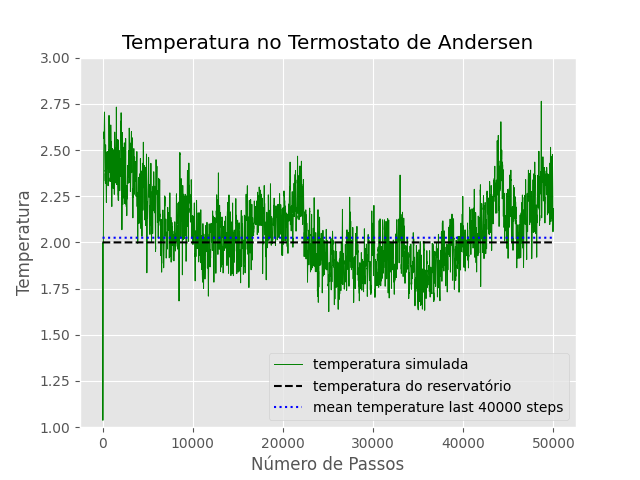
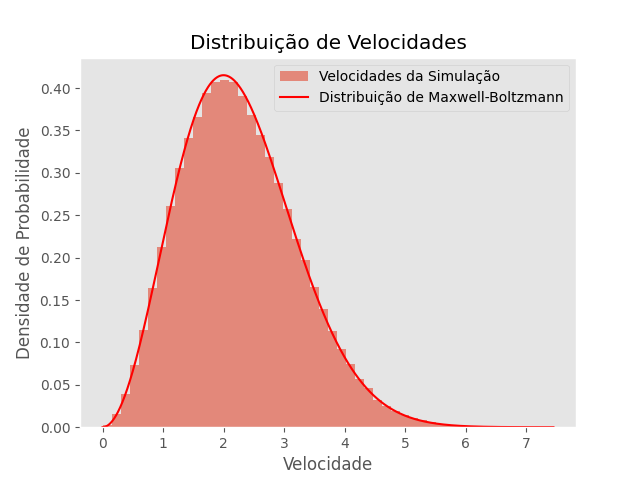
T=2 | === T=2 === | ||
<math>\mu = 2.025</math> | <math>\mu = 2.025</math> | ||
<math>\sigma = 0.166</math> | <math>\sigma = 0.166</math> | ||
| Linha 79: | Linha 83: | ||
T=3 | === T=3 === | ||
<math>\mu = 3.027</math> | <math>\mu = 3.027</math> | ||
<math>\sigma = 0.247</math> | <math>\sigma = 0.247</math> | ||
Edição das 20h26min de 9 de dezembro de 2024
INTRODUÇÃO
A dinâmica molecular é uma técnica que naturalmente simula sistemas clássicos compostos por N partículas interagindo dentro de um volume V. Nesse contexto, as posições das partículas são atualizadas com base no potencial de interação escolhido. Sob a suposição de ergodicidade — ou seja, que as médias temporais equivalem às médias de ensemble —, as simulações resultam em amostragens do ensemble microcanônico (NVE). Nesse ensemble, o número de partículas N, o volume V, e a energia total E permanecem constantes (aproximadamente).
Ao colocar um sistema em contato com um reservatório térmico a uma temperatura T, mudamos do ensemble microcanônico (NVE), onde a energia é mantida constante, para o ensemble canônico (NVT), no qual a temperatura do sistema é constante. Nesse novo ensemble, a distribuição de probabilidade das velocidades das partículas segue a forma da distribuição de Maxwell-Boltzmann, uma distribuição gaussiana associada à temperatura T. Um dos métodos mais simples para realizar uma amostragem correta do ensemble canônico é o termostato de Andersen. Neste estudo, focaremos na análise desse termostato, explorando sua implementação, características e aplicação na simulação de sistemas termodinâmicos.
FUNDAMENTO TEÓRICO E DETALHES DA IMPLEMENTAÇÃO
Temperatura
A definição de temperatura em um sistema clássico em função das velocidades das partículas pode ser obtida pela equipartição de energia:
Temos então:
onde é o número de graus de liberdade do sistema. No ensemble microcanônico, como o momento é conservado, temos , mas no ensemble canônico, e portanto no termostato de Andersen, o momento não é conservado e utilizamos .
Condições de Contorno Periódicas
As condições de contorno periódicas são fundamentais para garantir que simulações computacionais de sistemas físicos representem com precisão o comportamento de sistemas grandes e infinitos. Elas ajudam a evitar efeitos de borda que não são representativos do comportamento real de partículas em um espaço muito grande, permitindo simulações mais realistas e precisas.
É utilizada a convenção da imagem mínima, que calcula a menor distância entre as partículas, sendo essa sempre menor ou igual a .
Integração de Velocity-Verlet
Escolhido principalmente por não ser de ORDEM N² como o RK2, por exemplo. Precisamos calcular apenas 1 vez a força em cada passo do algoritmo. Assim, é o melhor "custo-benefício" dentre os possíveis algoritmos, tendo uma precisão razoável.
Condições Iniciais
Em todas as simulações, foram escolhidas as posições iniciais das partículas em uma grade cúbica igualmente espaçadas, para evitar que as partículas iniciem muito próximas, causando erros devido ao potencial entre as partículas, que no caso do Lennard-Jones cresce muito rápido quando as partículas se aproximam demais.
As velocidades foram escolhidas a partir de uma distribuição uniforme no intervalo , sendo reescaladas para a temperatura do reservatório, apesar de não fazer diferença para a convergência do algoritmo.
Potencial de Lennard-Jones
Unidades Adimensionais
TERMOSTATO DE ANDERSEN
Para simular o contato do sistema com um reservatório térmico, a cada passo de tempo Δt é realizado um procedimento de Monte Carlo. Nesse processo, N partículas são selecionadas aleatoriamente, uma de cada vez, e suas velocidades são atualizadas. Essas novas velocidades são sorteadas a partir da distribuição gaussiana centrada em zero com . Essa abordagem introduz um elemento de estocasticidade ao modelo, permitindo que a temperatura média do sistema oscile em torno da temperatura T do reservatório.
Na prática, a interação entre o sistema e o reservatório é controlada pela frequência de colisão . Para cada partícula, é gerado um número aleatório no intervalo [0,1]. Caso a velocidade da partícula é atualizada conforme descrito.
Algoritmo
Podemos descrever o algoritmo em 4 passos:
1. Inicia-se com um conjunto de posições e velocidades.
2. Integra-se as equações do movimento para um passo .
3. N partículas são selecionadas para colidir com o reservatório térmico.
4. Para cada partícula selecionada, definir nova velocidade a partir da distribuição de Maxwell-Boltzmann correspondente à temperatura T do reservatório.
RESULTADOS
Para verificar se o termostato está corretamente simulando o ensemble canônico, foram escolhidas 3 temperaturas diferentes. Para cada uma delas, foi simulado n=108 partículas, com densidade p=0.8442, nu=0.5, dt=0.001 e número de passos N=50.000. São mostradas abaixo a série temporal para cada uma das temperaturas. Para checar de forma mais consistente se o sistema no equilíbrio realmente corresponde ao ensemble canônico, foi comparada a curva teórica da distribuição de Maxwell-Boltzmann para a temperatura correspondente, com um histograma das velocidades em todas as dimensões obtidas nos últimos 40.000 passos (os primeiros 10.000 passos é o transiente para o equilíbrio). Além disso, foi calculada a média e o desvio-padrão para cada uma dessas medidas.
T=1
T=2
T=3







![{\displaystyle [-0.5,0.5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f82e0cb567f3dc7df3709b7077b346272589753)