Termostato de Andersen: mudanças entre as edições
| Linha 8: | Linha 8: | ||
=== Temperatura === | === Temperatura === | ||
<math> | |||
\[ | \[ | ||
\left\langle \frac{1}{2} m v_\alpha^2 \right\rangle = \frac{1}{2} k_B T | \left\langle \frac{1}{2} m v_\alpha^2 \right\rangle = \frac{1}{2} k_B T | ||
\] | \] | ||
</math> | |||
== TERMOSTATO DE ANDERSEN == | == TERMOSTATO DE ANDERSEN == | ||
Edição das 19h26min de 9 de dezembro de 2024
INTRODUÇÃO
A dinâmica molecular é uma técnica que naturalmente simula sistemas clássicos compostos por N partículas interagindo dentro de um volume V. Nesse contexto, as posições das partículas são atualizadas com base no potencial de interação escolhido. Sob a suposição de ergodicidade — ou seja, que as médias temporais equivalem às médias de ensemble —, as simulações resultam em amostragens do ensemble microcanônico (NVE). Nesse ensemble, o número de partículas N, o volume V, e a energia total E permanecem constantes (aproximadamente).
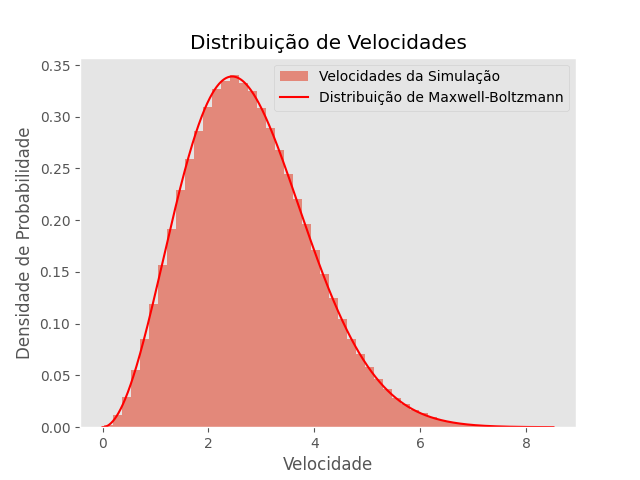
Ao colocar um sistema em contato com um reservatório térmico a uma temperatura T, mudamos do ensemble microcanônico (NVE), onde a energia é mantida constante, para o ensemble canônico (NVT), no qual a temperatura do sistema é constante. Nesse novo ensemble, a distribuição de probabilidade das velocidades das partículas segue a forma da distribuição de Maxwell-Boltzmann, uma distribuição gaussiana associada à temperatura T. Um dos métodos mais simples para realizar uma amostragem correta do ensemble canônico é o termostato de Andersen. Neste estudo, focaremos na análise desse termostato, explorando sua implementação, características e aplicação na simulação de sistemas termodinâmicos.
FUNDAMENTO TEÓRICO
Temperatura
Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \[ \left\langle \frac{1}{2} m v_\alpha^2 \right\rangle = \frac{1}{2} k_B T \] }
TERMOSTATO DE ANDERSEN
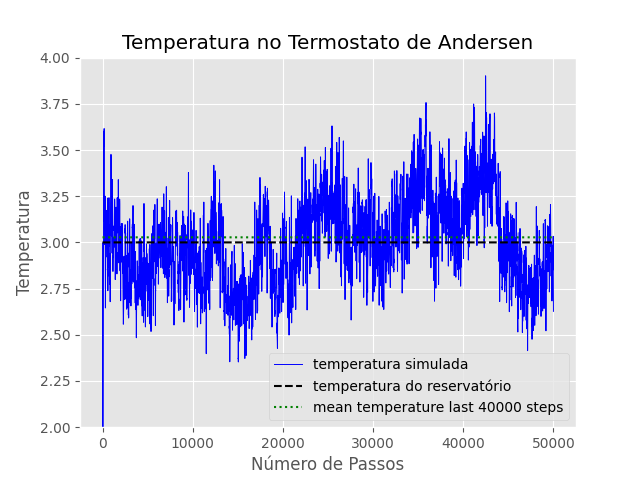
Para simular o contato do sistema com um reservatório térmico, a cada passo de tempo Δt é realizado um procedimento de Monte Carlo. Nesse processo, N partículas são selecionadas aleatoriamente, uma de cada vez, e suas velocidades são atualizadas. Essas novas velocidades são sorteadas a partir da distribuição gaussiana centrada em zero com . Essa abordagem introduz um elemento de estocasticidade ao modelo, permitindo que a temperatura média do sistema oscile em torno da temperatura T do reservatório.
Na prática, a interação entre o sistema e o reservatório é controlada pela frequência de colisão . Para cada partícula, é gerado um número aleatório no intervalo [0,1]. Caso a velocidade da partícula é atualizada conforme descrito.
Algoritmo
Podemos descrever o algoritmo em 4 passos:
1. Inicia-se com um conjunto de posições e velocidades.
2. Integra-se as equações do movimento para um passo .
3. N partículas são selecionadas para colidir com o reservatório térmico.
4. Para cada partícula selecionada, definir nova velocidade a partir da distribuição de Maxwell-Boltzmann correspondente à temperatura T do reservatório.
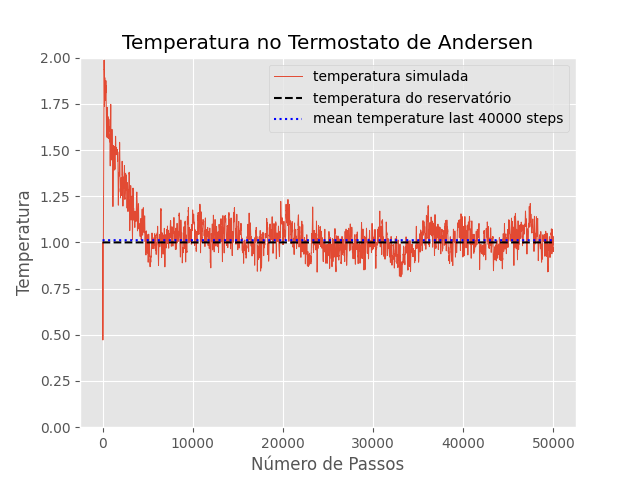
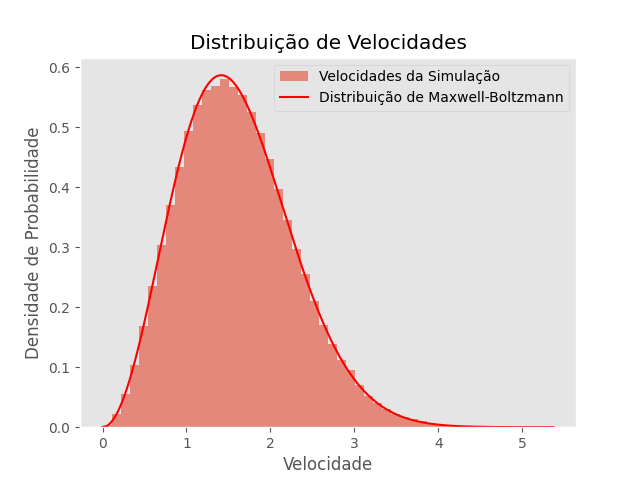
RESULTADOS
T=1
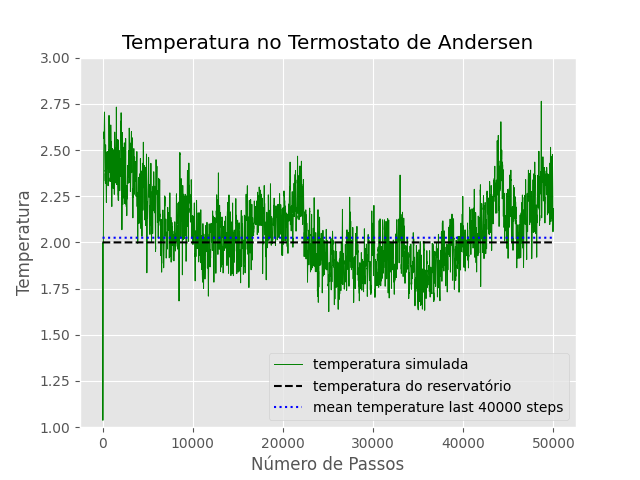
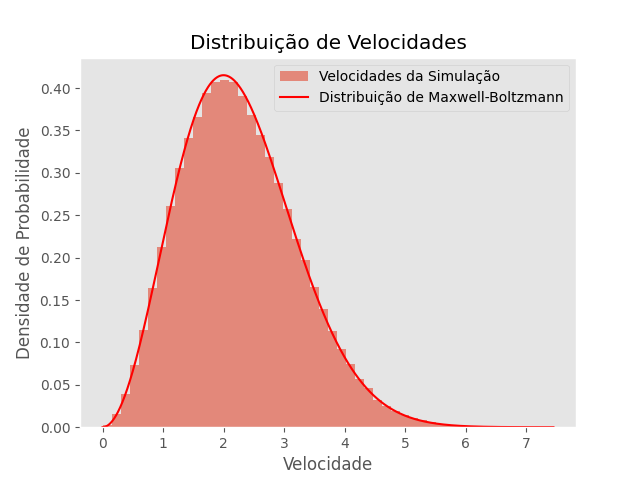
T=2
T=3