Equação de Dirac: mudanças entre as edições
| (25 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 2: | Linha 2: | ||
=Introdução= | =Introdução= | ||
A equação de Dirac descreve uma partícula relativística de spin <math>\frac{1}{2}</math>, como o elétron, com estrutura análoga | A equação de Dirac descreve uma partícula relativística de spin <math>\frac{1}{2}</math>, como o elétron, com estrutura análoga à da equação de Schrödinger. Ela surgiu inicialmente como tentativa de explicar discrepâncias entre experimentos e teoria para o espectro do átomo de hidrogênio, possibilitando correções para o cálculo da energia do elétron em diferentes níveis (as chamadas correções de ''estrutura fina''). Além disso, por meio dela foi possível prever a existência de antimatéria: descrevendo o elétron, ela também descreve o pósitron. | ||
A fim de compatibilizar a Mecânica Quântica com a Relatividade Especial, a equação diferencial parcial é de ''primeira'' ordem tanto no tempo quanto no espaço (diferentemente da equação de Schrödinger, que é de ''segunda'' ordem no espaço). A equação de Dirac pode ser escrita de diversas formas; aqui, apresentamo-la explicitamente como um sistema de EDPs acopladas, mais conveniente para os propósitos do trabalho. | A fim de compatibilizar a Mecânica Quântica com a Relatividade Especial, a equação diferencial parcial é de ''primeira'' ordem tanto no tempo quanto no espaço (diferentemente da equação de Schrödinger, que é de ''segunda'' ordem no espaço). A equação de Dirac pode ser escrita de diversas formas; aqui, apresentamo-la explicitamente como um sistema de EDPs acopladas, mais conveniente para os propósitos do trabalho. | ||
| Linha 523: | Linha 523: | ||
==Método Leap-frog== | ==Método Leap-frog== | ||
O método de Leap-frog (LF) é um método | O método de Leap-frog (LF) é um método explícito, contendo apenas termos em um mesmo instante do tempo no cálculo das derivadas espaciais. Na simulação realizada, utilizou-se a equação de Dirac em duas dimensões com potencial magnético nulo: | ||
<center> | <center> | ||
<math> | <math> | ||
i \partial_t \mathbf{\Phi} = [-\frac{i}{\varepsilon}(\sigma_1\partial_x+\sigma_2\partial_y) + \frac{1}{\varepsilon^2}\sigma_3] \mathbf{\Phi} + [V(t,x)I_2] \mathbf{\Phi} | i \partial_t \mathbf{\Phi} = \left[-\frac{i}{\varepsilon}(\sigma_1\partial_x+\sigma_2\partial_y) + \frac{1}{\varepsilon^2}\sigma_3 \right] \mathbf{\Phi} + [V(t,x)I_2] \mathbf{\Phi} | ||
</math> | </math> | ||
</center> | </center> | ||
onde se utiliza um parâmetro de escala <math>\varepsilon \in (0,1]</math>, conforme [[Equação_de_Dirac#Referências|(3)]]. Esse parâmetro está relacionado com a escolha de unidades do problema, e determina o comportamento relativístico do sistema estudado: quando <math>\varepsilon \to 0</math>, estamos no limite não relativístico; quando <math>\varepsilon \to 1</math>, estamos no limite relativístico com a velocidade da onda <math>v \to c</math>. | |||
Enuncia-se o método LF como: | |||
<center> | <center> | ||
<math> | <math> | ||
i \partial_t \mathbf{\Phi}_{i,j}^{n} = [-\frac{i}{\varepsilon}(\sigma_1\partial_x+\sigma_2\partial_y) + \frac{1}{\varepsilon^2}\sigma_3] \mathbf{\Phi}_{i,j}^{n} + [V(t,x)I_2] \mathbf{\Phi}_{i,j}^{n} | i \partial_t \mathbf{\Phi}_{i,j}^{n} = \left[-\frac{i}{\varepsilon}(\sigma_1\partial_x+\sigma_2\partial_y) + \frac{1}{\varepsilon^2}\sigma_3 \right] \mathbf{\Phi}_{i,j}^{n} + [V(t,x)I_2] \mathbf{\Phi}_{i,j}^{n} | ||
</math> | </math> | ||
</center> | </center> | ||
De forma análoga ao | De forma análoga ao caso de uma dimensão, é feita a discretização temporal e espacial. Utiliza-se a discretização temporal como <math>t_n=t0+n\Delta t</math> na dimensão <math>y</math> na forma <math>y_j=y_0+jh</math> e na dimensão <math>x</math> como <math>x_i=x_0+ih</math>, onde <math>j</math> e <math>i</math> são números inteiros. Em adição, discretiza-se as derivadas espaciais e temporal da seguinte forma: | ||
<center> | <center> | ||
| Linha 576: | Linha 578: | ||
</center> | </center> | ||
Ao substituir as derivadas pela forma discreta, e isolar o termo do passo termoral posterior, obtêm-se a forma final como: | |||
<center> | <center> | ||
<math> | <math> | ||
{\Phi_1}_{i,j}^{n+1}=-\frac{\Delta t}{h\varepsilon}[({\Phi_4}_{i+1,j}^{n}-{\Phi_4}_{i-1,j}^{n})-i({\Phi_4}_{i,j+1}^{n}-{\Phi_4}_{i,j-1}^{n})]-2i\Delta t[\frac{1}{\varepsilon^2}+V_{i,j}^{n}]{\Phi_1}_{i,j}^{n}+{\Phi_1}_{i,j}^{n-1} | {\Phi_1}_{i,j}^{n+1}=-\frac{\Delta t}{h\varepsilon} \left[({\Phi_4}_{i+1,j}^{n}-{\Phi_4}_{i-1,j}^{n})-i({\Phi_4}_{i,j+1}^{n}-{\Phi_4}_{i,j-1}^{n}) \right]-2i\Delta t \left[\frac{1}{\varepsilon^2}+V_{i,j}^{n} \right]{\Phi_1}_{i,j}^{n}+{\Phi_1}_{i,j}^{n-1} | ||
</math> | </math> | ||
</center> | </center> | ||
| Linha 586: | Linha 588: | ||
<center> | <center> | ||
<math> | <math> | ||
{\Phi_4}_{i,j}^{n+1}=-\frac{\Delta t}{h\varepsilon}[({\Phi_1}_{i+1,j}^{n}-{\Phi_1}_{i-1,j}^{n})+i({\Phi_1}_{i,j+1}^{n}-{\Phi_1}_{i,j-1}^{n})]+2i\Delta t[\frac{1}{\varepsilon^2}+V_{i,j}^{n}]{\Phi_4}_{i,j}^{n}+{\Phi_4}_{i,j}^{n-1} | {\Phi_4}_{i,j}^{n+1}=-\frac{\Delta t}{h\varepsilon} \left[({\Phi_1}_{i+1,j}^{n}-{\Phi_1}_{i-1,j}^{n})+i({\Phi_1}_{i,j+1}^{n}-{\Phi_1}_{i,j-1}^{n}) \right]+2i\Delta t \left[\frac{1}{\varepsilon^2}+V_{i,j}^{n} \right]{\Phi_4}_{i,j}^{n}+{\Phi_4}_{i,j}^{n-1} | ||
</math> | </math> | ||
</center> | </center> | ||
| Linha 594: | Linha 596: | ||
Assumindo que o potencial <math>V</math> é independente do tempo, pode-se provar via método de von Neumann que o método de Leap-frog é estável | Assumindo que o potencial <math>V</math> é independente do tempo, pode-se provar via método de von Neumann que o método de Leap-frog é estável sob as condições: | ||
<center> | <center> | ||
| Linha 602: | Linha 604: | ||
</center> | </center> | ||
Para <math> h>0 </math> e <math> 0<\varepsilon \leq 1. </math> | Para <math> h>0 </math> e <math> 0<\varepsilon \leq 1. </math> [[Equação_de_Dirac#Referências|(3)]] | ||
=Simulações em Julia= | =Simulações em Julia= | ||
| Linha 952: | Linha 954: | ||
</source><br /> | </source><br /> | ||
==Equação 1D com potencial "escalar"== | ==Equação 1D com potencial "escalar"== | ||
Consideraremos agora o problema com o potencial "escalar" <math>V_{sc}</math>. Dentro do formalismo da relatividade, os potenciais podem ser classificados de acordo com o seu comportamento frente a uma transformação de Poincaré: o potencial <math>V</math> se transforma como um vetor (por isso chamado de potencial "vetor"), e o potencial <math>V_{sc}</math>, como um escalar (potencial "escalar"). Como exemplo de potencial do tipo vetor, temos os potenciais eletromagnéticos; e de potencial do tipo escalar, pode-se citar modelos de confinamento. Na prática, pode-se dizer que o potencial <math>V_{sc}</math> altera a massa de repouso "efetiva" da partícula. Para este assunto, deixamos [[Equação_de_Dirac#Referências|(4)]] e [[Equação_de_Dirac#Referências|(5)]] como referências. | |||
Por ser um tópico bastante especializado, será considerado aqui apenas o caso do poço infinito. O problema é apenas uma extensão do que foi exposto [[Equação_de_Dirac#Poço Infinito|nessa seção]]; a [[Equação_de_Dirac#Método_de_Crank-Nicolson|discretização]] e a estabilidade do método de Crank-Nicolson são análogas, bastando apenas fazer <math>\alpha^n = 1 + \frac{i \Delta t}{2}(V^n _j + V_{{sc}_j}^n + 1)</math> e <math>\beta^n = 1 + \frac{i \Delta t}{2}(V^n _j - V_{{sc}_j}^n -1)</math>. | Por ser um tópico bastante especializado, será considerado aqui apenas o caso do poço infinito. O problema é apenas uma extensão do que foi exposto [[Equação_de_Dirac#Poço Infinito|nessa seção]]; a [[Equação_de_Dirac#Método_de_Crank-Nicolson|discretização]] e a estabilidade do método de Crank-Nicolson são análogas, bastando apenas fazer <math>\alpha^n = 1 + \frac{i \Delta t}{2}(V^n _j + V_{{sc}_j}^n + 1)</math> e <math>\beta^n = 1 + \frac{i \Delta t}{2}(V^n _j - V_{{sc}_j}^n -1)</math>. | ||
| Linha 1 139: | Linha 1 138: | ||
Passamos agora para o estudo da equação de Dirac em duas dimensões. Para tanto, a equação foi integrada utilizando-se o método de Leap-Frog, tanto com um potencial coulombiano central como com um potencial cossenoide. Em ambos casos, o potencial não depende do tempo e a condição inicial constituiu-se de um pacote gaussiano, centralizado em <math>(0,0)</math> para <math>\Phi_1</math> e em <math>(1,1)</math> para <math>\Phi_4</math>. | |||
O procedimento adotado segue o utilizado em [[Equação_de_Dirac#Referências|(3)]]. De forma aproximada, atribuiu-se para o passo temporal <math>n=1</math>: | |||
<center> | <center> | ||
<math> | <math> | ||
\mathbf{\Phi}_{i,j}^{1}=\mathbf{\Phi}_{i,j}^{0} -sin(\frac{\Delta t }{\varepsilon})\sigma_1(\delta_x+\delta_y)\mathbf{\Phi}_{i,j}^{0}-i(sin(\frac{\Delta t }{\varepsilon^2})\sigma_3+\Delta t V_{i,j}^{0} I_2)\mathbf{\Phi}_{i,j}^{0} | \mathbf{\Phi}_{i,j}^{1}=\mathbf{\Phi}_{i,j}^{0} -\sin \left(\frac{\Delta t }{\varepsilon} \right)\sigma_1(\delta_x+\delta_y)\mathbf{\Phi}_{i,j}^{0}-i \left(\sin\left(\frac{\Delta t }{\varepsilon^2}\right)\sigma_3+\Delta t V_{i,j}^{0} I_2\right)\mathbf{\Phi}_{i,j}^{0} | ||
</math> | </math> | ||
</center> | </center> | ||
Segue abaixo o código utilizado para ambos potenciais, | Segue abaixo o código utilizado para ambos potenciais, onde seu uso difere apenas em qual potencial foi comentado. A escolha do parâmetro de escala foi <math>\varepsilon = 0.8</math>. | ||
| Linha 1 156: | Linha 1 157: | ||
using Plots | using Plots | ||
using LinearAlgebra | using LinearAlgebra | ||
using LaTeXStrings | |||
using Printf | |||
function initial_values() | function initial_values() | ||
| Linha 1 163: | Linha 1 166: | ||
dt=0.01 | dt=0.01 | ||
ep=0.8 #0<ep<=1 -> := v/c | ep=0.8 #0<ep<=1 -> := v/c | ||
tmax=8. | |||
x=LinRange(-L,L,2*Int(L/h)) | x=LinRange(-L,L,2*Int(L/h)) | ||
| Linha 1 211: | Linha 1 215: | ||
end | end | ||
return L,h,dt,ep,x,y,V,psi1,psi4,nextpsi1,nextpsi4 | return L,h,dt,ep,tmax,x,y,V,psi1,psi4,nextpsi1,nextpsi4 | ||
end | end | ||
| Linha 1 217: | Linha 1 221: | ||
L,h,dt,ep,x,y,V,psi1,psi4,nextpsi1,nextpsi4=initial_values() | L,h,dt,ep,tmax,x,y,V,psi1,psi4,nextpsi1,nextpsi4=initial_values() | ||
#listas para salvar os frames do gif | #listas para salvar os frames do gif | ||
| Linha 1 227: | Linha 1 231: | ||
vv=deepcopy(psi4) | vv=deepcopy(psi4) | ||
t=0; | t=0; | ||
while t < tmax | while t < tmax | ||
| Linha 1 262: | Linha 1 266: | ||
end | end | ||
#montagem do gif | #montagem do gif | ||
function psi_anim(x,y, | function psi_anim(x,y,psi1,psi4,tmax) | ||
i=1 | i=1 | ||
anim = @animate while i<=length( | anim = @animate while i<=length(psi1) | ||
prob = abs2.(psi1[i])+abs2.(psi4[i]) | |||
t=0.01*i | t=0.01*i | ||
| Linha 1 277: | Linha 1 277: | ||
#titulo=@sprintf("| \Phi |^{2}em t = %f", | #titulo=@sprintf("| \Phi |^{2}em t = %f", | ||
u=2*L/h #exibe a malha de forma reduzida | u=2*L/h #exibe a malha de forma reduzida | ||
p = surface(x[Int(u/4):Int(3*u/4)],y[Int(u/4):Int(3*u/4)],prob[Int(u/4):Int(3*u/4),Int(u/4):Int(3*u/4)],title=titulo, xlabel = "x",ylabel="y",zlabel="Densidade de Probabilidade" ,zlim=(- | p = surface(x[Int(u/4):Int(3*u/4)],y[Int(u/4):Int(3*u/4)],prob[Int(u/4):Int(3*u/4),Int(u/4):Int(3*u/4)],title=titulo, xlabel = "x",ylabel="y",zlabel="Densidade de Probabilidade" ,zlim=(-0.5,1.75),clim=(0, maximum(prob))) | ||
i+= | i+=5 | ||
end | end | ||
arquivo = " | arquivo = "psi_coulomb.gif" | ||
gif(anim, arquivo, fps= | gif(anim, arquivo, fps=15) | ||
end | end | ||
psi_anim(x,y,anim_psi1,tmax) | psi_anim(x,y,anim_psi1,anim_psi4,tmax) | ||
| Linha 1 294: | Linha 1 293: | ||
===Potencial Coulombiano=== | ===Potencial Coulombiano=== | ||
Na animação gerada, nota-se | Na animação gerada, nota-se a dispersão para o infinito no momento inicial e o movimento semelhante a uma órbita que a curva de densidade de probabilidade <math>|\mathbf{\Phi}|^2</math> realiza em torno do centro do sistema de coordenadas, pois o potencial escolhido varia radialmente de forma positiva. Observa-se um padrão de ruído na parte central, o qual não foi estudado a fundo, mas, nesse caso, é exclusivo de pontos próximos ao ponto de divergência da função potencial. | ||
[[Arquivo:Psi_coulomb.gif]] | |||
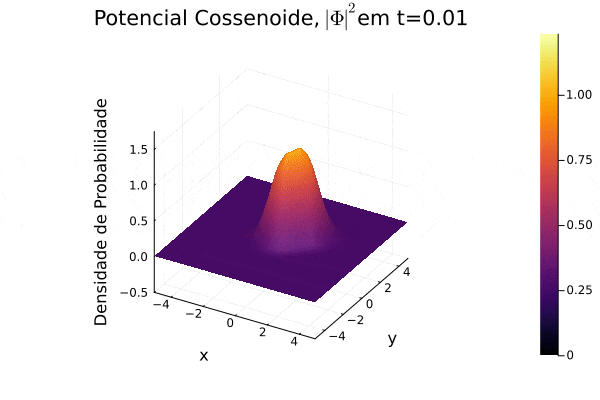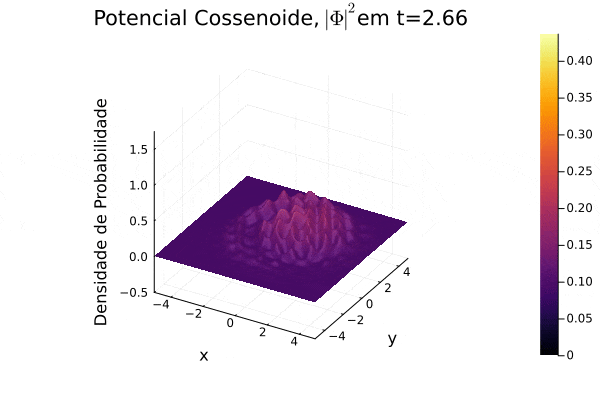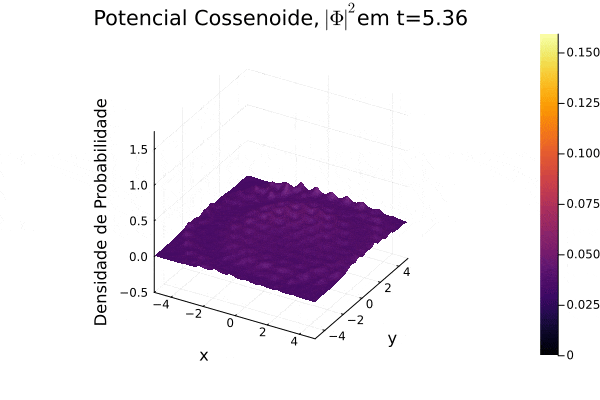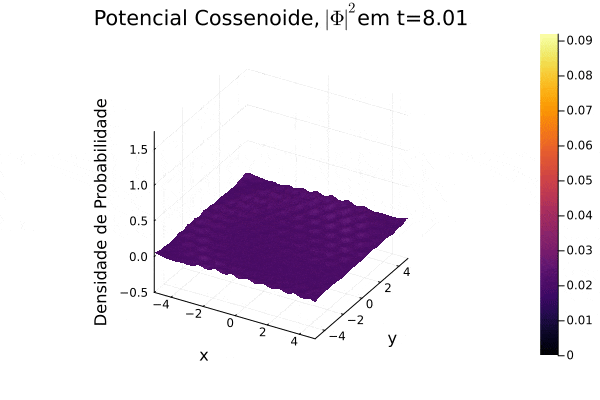
===Potencial Cossenoide=== | ===Potencial Cossenoide=== | ||
Reproduziu-se o potencial estudado | Reproduziu-se o potencial estudado em [[Equação_de_Dirac#Referências|(3)]], onde recebe o nome de "honeycomb potential". Observa-se, no período de tempo exibido, o espalhamento da função potencial no plano cartesiano e que a função densidade de probabilidade <math>|\mathbf{\Phi}|^2</math> forma um contorno de curva que se assemelha um favo de mel. | ||
[[Arquivo:Psi_cosin.gif]] | |||
=Referências= | =Referências= | ||
# The quantum theory of the electron. Proceedings of the Royal Society of London A, v. 117, n. 778, p. 610–624, fev. 1928. | # DIRAC, P. A. M. The quantum theory of the electron. Proceedings of the Royal Society of London A, v. 117, n. 778, p. 610–624, fev. 1928. | ||
# SAKURAI, J. J. Mecânica quântica moderna. 2. ed. Porto Alegre: Bookman, 2012. | # SAKURAI, J. J. Mecânica quântica moderna. 2. ed. Porto Alegre: Bookman, 2012. | ||
# BAO, W. et al. Numerical Methods and Comparison for the Dirac Equation in the Nonrelativistic Limit Regime. Journal of Scientific Computing, v. 71, n. 3, p. 1094–1134, jun. 2017. | # BAO, W. et al. Numerical Methods and Comparison for the Dirac Equation in the Nonrelativistic Limit Regime. Journal of Scientific Computing, v. 71, n. 3, p. 1094–1134, jun. 2017. | ||
# SOFF, G. et al. Solution of the Dirac Equation for Scalar Potentials and its Implications in Atomic Physics. Zeitschrift für Naturforschung A, v. 28, n. 9, p. 1389–1396, 1 set. 1973. | # SOFF, G. et al. Solution of the Dirac Equation for Scalar Potentials and its Implications in Atomic Physics. Zeitschrift für Naturforschung A, v. 28, n. 9, p. 1389–1396, 1 set. 1973. | ||
# THALLER, B. The Dirac equation. Berlin: Springer, 2010. | # THALLER, B. The Dirac equation. Berlin: Springer, 2010. | ||
Edição atual tal como às 15h25min de 27 de agosto de 2024
Grupo: André Luis Della Valentina, Lucas dos Santos Assmann, Vinícius Bayne Müller
Introdução
A equação de Dirac descreve uma partícula relativística de spin , como o elétron, com estrutura análoga à da equação de Schrödinger. Ela surgiu inicialmente como tentativa de explicar discrepâncias entre experimentos e teoria para o espectro do átomo de hidrogênio, possibilitando correções para o cálculo da energia do elétron em diferentes níveis (as chamadas correções de estrutura fina). Além disso, por meio dela foi possível prever a existência de antimatéria: descrevendo o elétron, ela também descreve o pósitron.
A fim de compatibilizar a Mecânica Quântica com a Relatividade Especial, a equação diferencial parcial é de primeira ordem tanto no tempo quanto no espaço (diferentemente da equação de Schrödinger, que é de segunda ordem no espaço). A equação de Dirac pode ser escrita de diversas formas; aqui, apresentamo-la explicitamente como um sistema de EDPs acopladas, mais conveniente para os propósitos do trabalho.
Assim como a equação de Schrödinger, a construção da equação de Dirac vem a partir do operador Hamiltoniano, que descreve a evolução temporal do estado quântico em questão:
onde, como anteriormente, os autovalores de correspondem aos valores possíveis de energia que o sistema pode assumir.
A mudança com relação à Mecânica Quântica não relativística acontece quando consideramos a energia relativística da partícula:
Assim, o Hamiltoniano é modificado para representar a medida da energia relativística total.
Diferentemente da equação de Schrödinger, aqui não representa apenas uma função de onda, mas sim um conjunto de quatro delas. Usando a notação
,
as componentes de representam as funções de onda associadas ao elétron e ao pósitron: () representa a função de onda do elétron com spin up (down), e () representa a função de onda do pósitron com spin up (down). O objeto é chamado de spinor.
Dedução da equação de Dirac em uma e duas dimensões
Consideraremos neste trabalho a equação de Dirac em uma e duas dimensões, e . A escolha dessas coordenadas se dá pela conveniência do acoplamento das EDPs: nesse caso, as quatro equações acopladas passam a ser acopladas duas a duas, facilitando o estudo do sistema. A dedução aqui apresentada é baseada em (1) e (2).
Construção do Hamiltoniano completo
Consideremos uma partícula sob ação de um potencial (onde ), que afeta a energia potencial da partícula, e de um potencial "escalar" , que afeta a massa de repouso da mesma. Seguindo uma das propostas possíveis para o Hamiltoniano, temos
onde ; e são matrizes 4x4 adimensionais e é o vetor momento linear da partícula.
Pode-se mostrar que e devem satisfazer certos vínculos, limitando as escolhas possíveis para essas matrizes. A escolha mais simples e usualmente adotada consiste em tomar
Sendo , podemos escrever o produto escalar como
Portanto, em notação matricial o Hamiltoniano pode ser escrito como
Unidades naturais e redução para duas dimensões
A fim de simplificar o formalismo, adotamos as chamadas "unidades naturais", onde . Note que isso equivale a reescalar as quantidades físicas do problema por um fator adequado. Ao fazer , também assumimos que a partícula está no limite relativístico.
Além disso, queremos estudar o problema em duas dimensões. Observamos que ; logo, . Portanto, temos o Hamiltoniano simplificado
Forma explícita final
Retornando ao problema original, queremos resolver
Novamente utilizando a notação matricial, obtemos
Realizando a multiplicação matricial, pode-se ver que se obtém dois sistemas acoplados: com e com . Escolhendo o sistema de com :
Simplificando e isolando a derivada temporal, obtemos por fim
Por fim, a equação em uma dimensão () é facilmente obtida: basta fazer
Neste trabalho, serão considerados principalmente problemas apenas com o potencial ; assim, caso indicado o contrário, será assumido .
Discretização
A equação de Dirac 1D pode ser escrita, na forma matricial, como
onde e é matriz identidade de dimensão 2. As matrizes de Pauli são escritas, aqui, como e .
Para discretizar uma equação diferencial parcial como essa, é necessário discretizar o espaço e o tempo. Convenciona-se como um passo finito de tempo e como um passo finito no espaço, de tal forma que , onde são números inteiros. Define-se a notação e também . Discretiza-se as derivadas parciais explicitamente com uma expansão em série de taylor da própria função:
Considerando uma derivada discretizada e truncando na primeira ordem:
O processo é completamente análogo para a derivada espacial, porém para facilitar a aplicação do método mantém-se o espaço centrado em , em outras palavras faz-se uma expansão em torno de , obtendo:
Com isso, obtém-se uma equação para um método explícito no tempo da equação de Dirac 1D.
Pode-se também desenvolver um método implícito no tempo fazendo a expansão de em torno de , obtendo:
Ao aplicar esta aproximação na equação discretizada basta dar um passo a frente em todos os elementos, obtendo um método implícito no tempo, já que há dependência com .
Neste trabalho, foram utilizados dois métodos de integração numérica diferentes: o de Crank-Nicolson, para a equação de Dirac em uma dimensão, e o de Leap-Frog, para a equação em duas dimensões. Deixamos (3) como referência para estes e outros métodos numéricos aplicados ao problema.
Método de Crank-Nicolson
O método de Crank-Nicolson (CN) consiste em uma média entre um método explícito e outro implícito no espaço. Utilizar-se-á a notação para representar justamente a média entre ambos os métodos, ou seja:
Define-se a notação:
Dessa maneira, enuncia-se o método CN para a equação de Dirac 1D como:
,
onde são as discretizações explícitas das derivadas.
Para que seja possível aplicar e estudar o método, é necessário passar da notação matricial para escalar:
Isolando cada tempo em um lado da igualdade:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2\right]\mathbf{\Phi^{n+1} _j} + \frac{\Delta t}{4h}\sigma_1\left[\mathbf{\Phi^{n+1} _{j+1}} - \mathbf{\Phi^{n+1} _{j-1}}\right] = }
Abrindo as matrizes Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_1, \sigma_3}
e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_2}
e operando-as sobre o vetor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\Phi}}
na equação, tem-se:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} +\frac{i\Delta t}{2} \begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix} + \frac{i}{2}\Delta t V^{n+1} _j \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}\right) \begin{bmatrix} \psi^{n+1} _{1,j} \\ \psi^{n+1} _{4,j} \\ \end{bmatrix} +\frac{\Delta t}{4h} \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} \psi^{n+1} _{1,j+1} - \psi^{n+1} _{1,j-1} \\ \psi^{n+1} _{4,j+1} - \psi^{n+1} _{4,j-1} \\ \end{bmatrix} = \left(\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} -\frac{i\Delta t}{2} \begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix} -\frac{i}{2}\Delta t V^{n} _j \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}\right) \begin{bmatrix} \psi^{n} _{1,j} \\ \psi^{n} _{4,j} \\ \end{bmatrix} -\frac{\Delta t}{4h} \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} \psi^{n} _{1,j+1} - \psi^{n} _{1,j-1} \\ \psi^{n} _{4,j+1} - \psi^{n} _{4,j-1} \\ \end{bmatrix} }
Pode-se realizar as operações matriciais e escrever duas equações escalares. Para facilitar a notação, utiliza-se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^n _j = \psi^n _{1,j}}
e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g^n _j = \psi^n _{4,j}}
:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \left[1 + \frac{i \Delta t}{2}(V^{n+1} _j + 1)\right]f^{n+1} _j + \frac{\Delta t}{4h}(g^{n+1}_{j+1} - g^{n+1}_{j-1}) = \left[1 - \frac{i \Delta t}{2}(V^{n} _j + 1)\right]f^{n} _j - \frac{\Delta t}{4h}(g^{n}_{j+1} - g^{n}_{j-1}) \\ \left[1 + \frac{i \Delta t}{2}(V^{n+1} _j - 1)\right]g^{n+1} _j + \frac{\Delta t}{4h}(f^{n+1}_{j+1} - f^{n+1}_{j-1} ) = \left[1 - \frac{i \Delta t}{2}(V^{n} _j - 1)\right]g^{n} _j - \frac{\Delta t}{4h}(f^{n}_{j+1} - f^{n}_{j-1}) \end{cases} }
Tem-se então um número Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n}
de equações onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n}
é o número de elementos do espaço discretizado. Portanto o primeiro termo das duas equações gera uma matriz diagonal, pois multiplica os termos espaciais dependentes de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_j}
; já o segundo termo gera uma matriz tridiagonal com diagonal principal nula. Nota-se que os primeiros termos dos dois lados da igualdade são o conjugado um do outro: define-se, portanto, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha^n = 1 + \frac{i \Delta t}{2}(V^{n+1} _j + 1)}
e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = 1 + \frac{i \Delta t}{2}(V^{n+1} _j - 1)}
.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \alpha^{n+1}f^{n+1} _j + \dfrac{\Delta t}{4h}(g^{n+1}_{j+1} - g^{n+1}_{j-1}) = \alpha^{n^*}f^{n} _j - \dfrac{\Delta t}{4h}(g^{n}_{j+1} - g^{n}_{j-1} ) \\ \beta^{n+1}g^{n+1} _j + \dfrac{\Delta t}{4h}(f^{n+1}_{j+1} - f^{n+1}_{j-1} ) = \beta^{n^*}g^{n} _j - \dfrac{\Delta t}{4h}(f^{n}_{j+1} - f^{n}_{j-1}) \end{cases} }
Considerando que o potencial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V}
é só função da posição, escreve-se o método como:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} Af^{n+1} + Bg^{n+1} = A^*f^n - Bg^n \\ Cg^{n+1} + Bf^{n+1} = C^*g^n - Bf^n \\ \end{cases} } ,
onde
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = \begin{bmatrix} \alpha & 0 & 0 & \cdots & 0\\ 0 & \alpha & 0 & \cdots & 0 \\ 0 & 0 & \alpha & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & \cdots & \cdots & \alpha \\ \end{bmatrix}; \quad B = \begin{bmatrix} 0 & \frac{\Delta t}{4h} & 0 & \cdots & 0\\ -\frac{\Delta t}{4h} & 0 & \frac{\Delta t}{4h} & \cdots & 0 \\ 0 & -\frac{\Delta t}{4h} & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ 0 & \cdots & \cdots & -\frac{\Delta t}{4h} & 0 \\ \end{bmatrix}; \quad C = \begin{bmatrix} \beta & 0 & 0 & \cdots & 0\\ 0 & \beta & 0 & \cdots & 0 \\ 0 & 0 & \beta & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & \cdots & \cdots & \beta \\ \end{bmatrix} } .
Por fim, pode-se escrever o método resolvendo o sistema
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} f^{n+1} = F^{-1}D f^n -F^{-1}E g^n \\ g^{n+1} = J^{-1}G f^n - J^{-1}H g^n \\ \end{cases} } ,
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D = (B^{-1}A^* + C^{-1}B)} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E = (I + C^{-1}C^*)} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = (B^{-1}A - C^{-1}B)} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle G = (A^{-1}A^* + I)} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = (A^{-1}B + B^{-1}C^*)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J= (A^{-1}B - B^{-1}C)} .
Com isso, e com condições iniciais e de contorno bem estabelecidas, já é possível aplicar o método, dado que todas essas matrizes dependem somente dos parâmetros do sistema.
Estabilidade Crank-Nicolson
Utilizar-se-á o método de von Neumann para analisar a estabilidade do método de Crank-Nicolson para a equação de Dirac unidimensional. Para tanto, supõe-se que a função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\Phi^{n} _j}} pode ser dada pela série de Fourier
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\Phi^{n} _j} = \sum_{k=0}^{\inf} \mathbf{A}^{n}e^{ikqjh} }
Devido à independência linear de cada termo do somatório, ao substituir na equação do método haverá uma equação para cada ente do somatório. Se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\frac{\mathbf{A}^{n+1}}{\mathbf{A}^{n}}\right| \le 1} , então pode-se dizer que o método estável, já que dessa forma garante-se uma não divergência.
Aplica-se um termo geral da série de índice Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} no método CN para a equação de Dirac 1D:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2\right]\mathbf{A}^{n+1}e^{ikqjh} + \frac{\Delta t}{4h}\sigma_1\mathbf{A}^{n+1}\left[e^{ikq(j+1)h} - e^{ikq(j-1)h}\right] = \left[I_2 - \frac{i}{2}\Delta t\sigma_3 - \frac{i}{2}\Delta t V^{n} _jI_2\right]\mathbf{A}^{n}e^{ikqjh} - \frac{\Delta t}{4h}\sigma_1\mathbf{A}^{n}\left[e^{ikq(j+1)h} - e^{ikq(j-1)h}\right] }
Divide-se tudo por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{ikqjh}} e isola-se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A}} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2 + \frac{\Delta t}{4h}\sigma_1\left(e^{ikqh} - e^{-ikqh}\right)\right]\mathbf{A}^{n+1}= \left[I_2 - \frac{i}{2}\Delta t\sigma_3 - \frac{i}{2}\Delta t V^{n} _jI_2 - \frac{\Delta t}{4h}\sigma_1\left(e^{ikqh} - e^{-ikqh}\right)\right]\mathbf{A}^{n} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2 + \frac{\Delta t}{4h}\sigma_1\left(\frac{\sin (kqh)}{2i}\right)\right]\mathbf{A}^{n+1}= \left[I_2 - \frac{i}{2}\Delta t\sigma_3 - \frac{i}{2}\Delta t V^{n} _jI_2 - \frac{\Delta t}{4h}\sigma_1\left(\frac{\sin (kqh)}{2i}\right)\right]\mathbf{A}^{n} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2 - \frac{i\Delta t}{4h}\sigma_1\left(\frac{\sin (kqh)}{2}\right)\right]\mathbf{A}^{n+1}= \left[I_2 - \frac{i}{2}\Delta t\sigma_3 - \frac{i}{2}\Delta t V^{n} _jI_2 + \frac{i\Delta t}{4h}\sigma_1\left(\frac{\sin (kqh)}{2}\right)\right]\mathbf{A}^{n} }
Nota-se que os termos que multiplicam o fator Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A}} são o conjugado um do outro. Define-se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_l} como a componente l escalarda multiplicação da matriz Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2 - \frac{i\Delta t}{4h}\sigma_1\left(\frac{\sin (kqh)}{2}\right)} pelo vetor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{{A_l}^{n+1}}{{A_l}^{n}} = \frac{z^*}{z} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\frac{{A_l}^{n+1}}{{A_l}^{n}}\right| = \left|\frac{z^*}{z}\right| = \frac{|z^*|}{|z|} = 1 } ,
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} é sempre diferente de zero, visto que a parte real é dada por uma matriz identidade constante.
Mostra-se, portanto, que a razão entre os coeficientes da série de Fourier nunca diverge, ou seja, o método é incondicionalmente estável.
Método Leap-frog
O método de Leap-frog (LF) é um método explícito, contendo apenas termos em um mesmo instante do tempo no cálculo das derivadas espaciais. Na simulação realizada, utilizou-se a equação de Dirac em duas dimensões com potencial magnético nulo:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \partial_t \mathbf{\Phi} = \left[-\frac{i}{\varepsilon}(\sigma_1\partial_x+\sigma_2\partial_y) + \frac{1}{\varepsilon^2}\sigma_3 \right] \mathbf{\Phi} + [V(t,x)I_2] \mathbf{\Phi} }
onde se utiliza um parâmetro de escala Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon \in (0,1]} , conforme (3). Esse parâmetro está relacionado com a escolha de unidades do problema, e determina o comportamento relativístico do sistema estudado: quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon \to 0} , estamos no limite não relativístico; quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon \to 1} , estamos no limite relativístico com a velocidade da onda Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v \to c} .
Enuncia-se o método LF como:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \partial_t \mathbf{\Phi}_{i,j}^{n} = \left[-\frac{i}{\varepsilon}(\sigma_1\partial_x+\sigma_2\partial_y) + \frac{1}{\varepsilon^2}\sigma_3 \right] \mathbf{\Phi}_{i,j}^{n} + [V(t,x)I_2] \mathbf{\Phi}_{i,j}^{n} }
De forma análoga ao caso de uma dimensão, é feita a discretização temporal e espacial. Utiliza-se a discretização temporal como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_n=t0+n\Delta t} na dimensão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} na forma Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_j=y_0+jh} e na dimensão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_i=x_0+ih} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} são números inteiros. Em adição, discretiza-se as derivadas espaciais e temporal da seguinte forma:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_t\mathbf{\Phi^n _{i,j}} = \frac{\mathbf{\Phi^{n+1} _{i,j}} - \mathbf{\Phi^{n-1} _{i,j}}}{2\Delta t} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_x\mathbf{\Phi^n _{i,j}} = \frac{\mathbf{\Phi^{n} _{i+1,j}} - \mathbf{\Phi^{n} _{i-1,j}}}{2h} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_y\mathbf{\Phi^n _{i,j}} = \frac{\mathbf{\Phi^{n} _{i,j+1}} - \mathbf{\Phi^{n} _{i,j-1}}}{2h} }
Primeiramente, reescreve-se o método na forma escalar como:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \partial_t {\Phi_1}_{i,j}^{ n} = -\frac{i}{\varepsilon}(\partial_x-i\partial_y) {\Phi_4}_{i,j}^{n} + \frac{1}{\varepsilon^2}{\Phi_1}_{i,j}^{n} + V(t,x){\Phi_1}_{i,j}^{n} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \partial_t {\Phi_4}_{i,j}^{n} = -\frac{i}{\varepsilon}(\partial_x+i\partial_y) {\Phi_1}_{i,j}^{n} - \frac{1}{\varepsilon^2}{\Phi_4}_{i,j}^{n} + V(t,x){\Phi_4}_{i,j}^{n} }
Ao substituir as derivadas pela forma discreta, e isolar o termo do passo termoral posterior, obtêm-se a forma final como:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\Phi_1}_{i,j}^{n+1}=-\frac{\Delta t}{h\varepsilon} \left[({\Phi_4}_{i+1,j}^{n}-{\Phi_4}_{i-1,j}^{n})-i({\Phi_4}_{i,j+1}^{n}-{\Phi_4}_{i,j-1}^{n}) \right]-2i\Delta t \left[\frac{1}{\varepsilon^2}+V_{i,j}^{n} \right]{\Phi_1}_{i,j}^{n}+{\Phi_1}_{i,j}^{n-1} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\Phi_4}_{i,j}^{n+1}=-\frac{\Delta t}{h\varepsilon} \left[({\Phi_1}_{i+1,j}^{n}-{\Phi_1}_{i-1,j}^{n})+i({\Phi_1}_{i,j+1}^{n}-{\Phi_1}_{i,j-1}^{n}) \right]+2i\Delta t \left[\frac{1}{\varepsilon^2}+V_{i,j}^{n} \right]{\Phi_4}_{i,j}^{n}+{\Phi_4}_{i,j}^{n-1} }
Estabilidade do Método Leap-frog
Assumindo que o potencial é independente do tempo, pode-se provar via método de von Neumann que o método de Leap-frog é estável sob as condições:
Para e (3)
Simulações em Julia
Equação 1D
Fez-se simulações do método de Crank-Nicolson para a equação de Dirac unidimensional em três configurações de potenciais diferentes: Nulo (Partícula Livre), Poço Infinito e Oscilador Harmônico Simples. Para todos os casos utilizou-se uma condição inicial de um pacote gaussiano de desvio padrão para uma das componentes de , sendo a outra componente nula. O módulo quadrado do pacote gaussiano deve ter área unitária dentro da malha utilizada (de até ), por isso a constante de normalização deve ser .
Segue trecho do código comum a todos as simulações realizadas; a única diferença é que em um caso do OHS o pacote gaussiano é deslocado do meio da malha para a posição .
using Plots
using LaTeXStrings
using LinearAlgebra
using Integrals
function init(x, sigma)
arg1 = @. ((-(x-25)^2)/(2*sigma^2))
arg2 = 1/sqrt(sqrt(pi)*sigma)
return arg2*exp.(arg1) ##Inicializo com um pacote gaussiano
end
function OHS(V,x, k)
V = @. 0.5*k*(x-25)^2
return V
end
function poco(V, h)
#Quero colocar nas posições 18 e 32
V[round(Int64, 18/h)] = 100000
V[round(Int64, 32/h)] = 100000
return V
end
##Matrizes do método de Crank-Nicholson
function matriz(dt,h,L, V)
A = Diagonal(ones(L).*(1 .+ im*dt*0.5.*(V.+1)))
B = LinearAlgebra.Tridiagonal(ones(L-1).*(-dt/(4*h)), zeros(L), ones(L-1).*(dt/(4*h)))
C = Diagonal(ones(L).*(1 .+ im*dt*0.5.*(V.-1)))
A = Array(A)
B = Array(B)
C = Array(C)
A_i = inv(A)
B_i = inv(B)
C_i = inv(C)
AiB = A_i*B
CiB = C_i*B
D = B_i*conj(A) + CiB
E = I(L) + C_i*conj(C)
F = B_i*A -CiB
G = A_i*conj(A) + I(L)
H = AiB + B_i*conj(C)
J = AiB - B_i*conj(C)
F_i = inv(F)
J_i = inv(J)
K = F_i*D
L = F_i*E
M = J_i*G
N = J_i*H
return K, L, M, N
end
function CN(size, h, tsize, V, dt, ci)
f = zeros(Complex, tsize, size) #Cada linha representa vetor posição em um tempo diferente. ## phi 1
g = zeros(Complex, tsize, size) ##phi 4
A, B, C, D = matriz(dt, h, size, V) #Matrizes do método Crank-Nicholson
f[1, :] = ci ##Condição Inicial
g[1, :] = zeros(size)
##Condições de Contorno
f[:, 1] = zeros(tsize)
f[:, end] = zeros(tsize)
g[:, 1] = zeros(tsize)
g[:, end] = zeros(tsize)
i=2 #Não interfiro nos contornos
while i<tsize
f[i, :] = A*f[i-1, :] - B*g[i-1, :]
g[i, :] = C*f[i-1, :] - D*g[i-1, :]
i+=1
end
return f, g
end
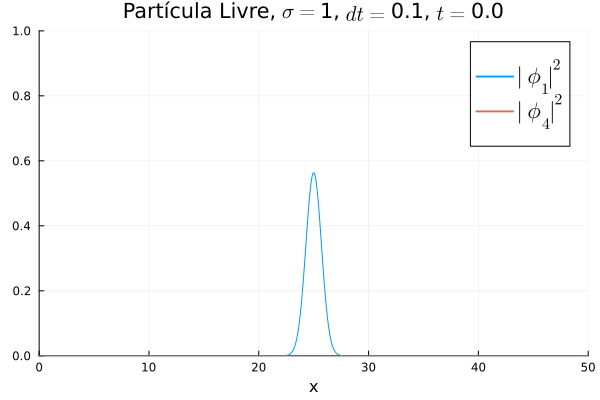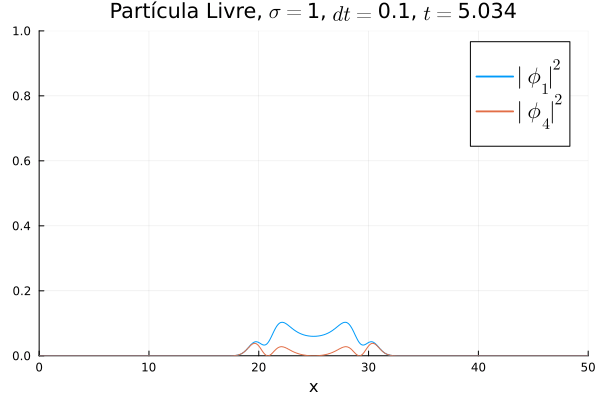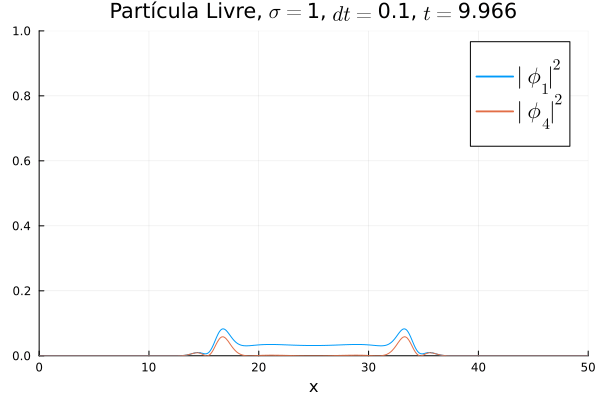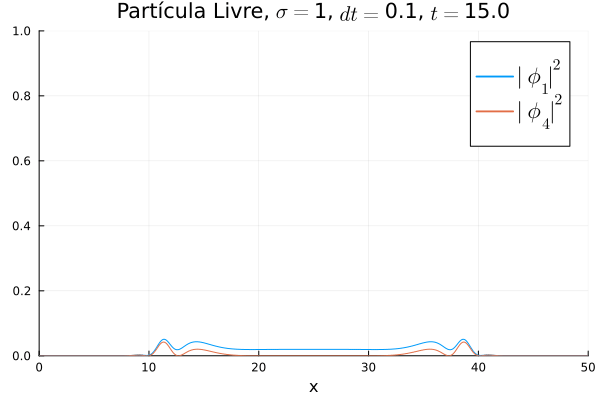
Partícula Livre
Aplicou-se o código demonstrado com potencial nulo para simular o caso da partícula livre. Segue abaixo código utilizado para gerar a animação:
Nota-se que mesmo que seja nula no início, a existência da partícula (neste caso, o elétron com spin up) gera a outra (pósitron com spin down). O comportamento é de dispersão, ou seja, a tendência é que a posição fique cada vez menos definida: a partícula livre, por estar fora da ação de um potencial, apresenta momento bem definido; pelo Princípio da Incerteza, a posição torna-se incerta. Nota-se também que as bordas estão longe o suficiente na escala de tempo utilizada, de maneira que as condições de contorno não afetam a simulação.
function main()
L = 50 #Dimensão espacial matriz
k=0.1 #"Constante Elástica" do oscilador harmônico
sigma = 1 #Largura do pacote gaussiano
dt = 0.02
size= 10*L
h = L/size ##Passo espacial
tmax = 15
tsize = round(Int64, tmax/dt) #Tamanho do vetor tempo
t = LinRange(0, tmax, tsize)
x = LinRange(0, L, size)
V = zeros(size)
xi = init(LinRange(0, L, size), sigma) #Condição inicial pacote gaussiano
f,g =CN(size,h,tsize, V, dt,xi)
i=1
anim = @animate while i<=tsize
f_real = real(f[i, :])
f_imag = imag(f[i, :])
g_real = real(g[i, :])
g_imag = imag(g[i, :])
probf = abs2.(f[i, :])
probg = abs2.(g[i, :])
prob = probf + probg
p=plot(x, probf, label=L"$|\phi_1|^2$", legendfont=font(15))
plot!(x, probg, label=L"$|\phi_4|^2$", legendfont=font(15))
titulo = "Partícula Livre"*", "*L"$\sigma=$"*string(sigma)*", "* L"$dt=$"*string(dt)* ", " *L"$t=$" * string(round(t[i], digits=3))
plot!(title=titulo,
xlabel = "x",
xlim=(0,50),
xticksfont = font(13),
ticksfontsize = 10,
ylim=(0,1),
yticksfont=font(13),
)
i+=1
end
arquivo = "diracfree.gif"
gif(anim, arquivo, fps=30)
end
main()
Poço Infinito
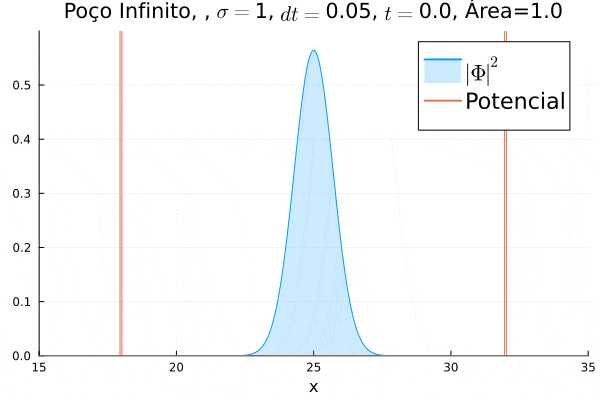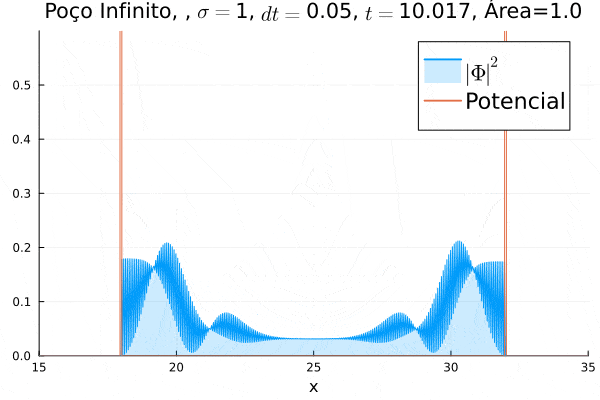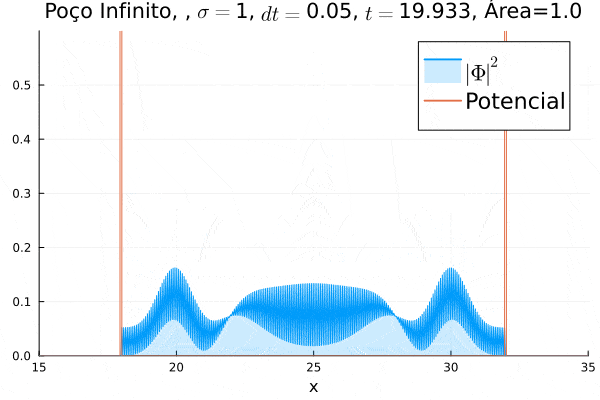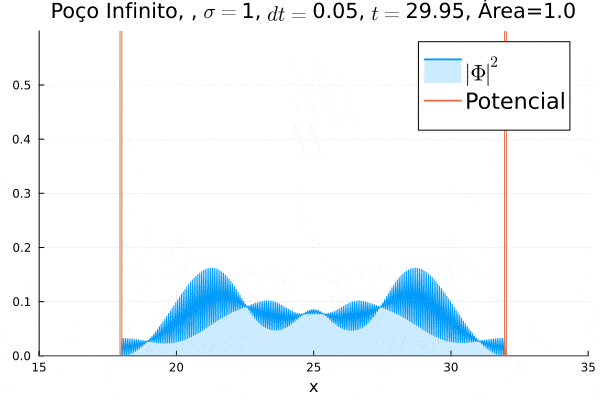
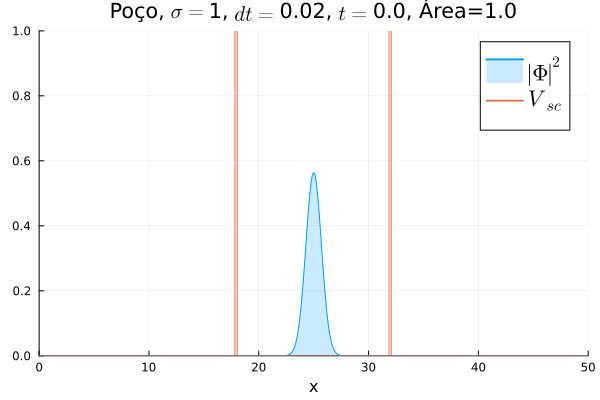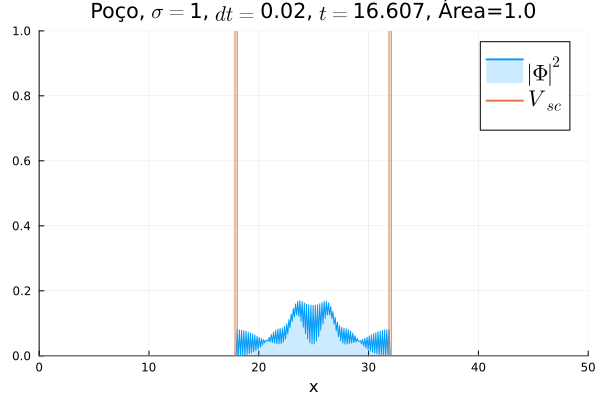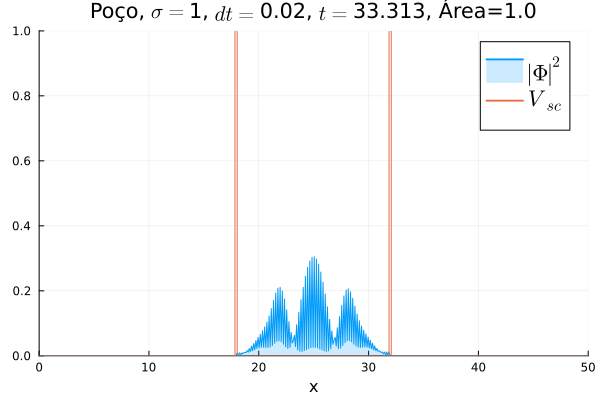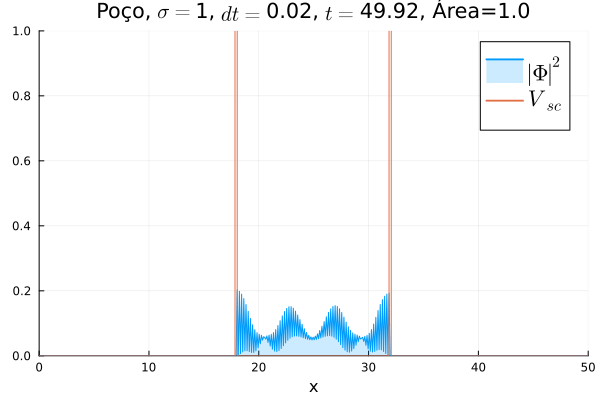
O poço infinito foi simulado colocando dois potenciais muito grandes em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=18} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=32} . Abaixo está reproduzida a animação.
Nota-se que a função simulada é a soma dos quadrados dos módulos de cada função de onda (elétron e pósitron); é a integral de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Phi|^2 = |\phi_1|^2+|\phi_4|^2} que deve sempre ser unitária, o que concorda com o obtido. Na animação é possível perceber um comportamento semelhante ao de uma onda estacionária, onde tem-se vários "harmônicos" associados ao pacote de ondas: como esperado, a função de onda é uma combinação linear dos autoestados do poço infinito.
Segue trecho do código utilizado para gerar a animação:
function main()
L = 50 #Dimensão espacial matriz
sigma = 1 #Largura do pacote gaussiano
dt = 0.05 #Passo temporal
size= 30*L #Utilizado para definir o passo espacial
h = L/size #Passo espacial
tmax = 30 #
tsize = round(Int64, tmax/dt) tamanho do vetor tempo.
t = LinRange(0, tmax, tsize)
x = LinRange(0, L, size)
V = zeros(size)
xi = init(LinRange(0, L, size), sigma) #Condição inicial de pacote gaussiano centralizado em x=25
#V = OHS(V,x,k)
V = poco(V, h) #Inicializa o potencial
f,g =CN(size,h,tsize, V, dt,xi) #Obtém as funções de onda e sua respectiva evolução temporal
##Produz-se a animação
i=1
anim = @animate while i<=tsize
f_real = real(f[i, :])
f_imag = imag(f[i, :])
g_real = real(g[i, :])
g_imag = imag(g[i, :])
probf = abs2.(f[i, :])
probg = abs2.(g[i, :])
prob = probf + probg
problem = SampledIntegralProblem(prob, x) #Resolve a integral em cada tempo, calculando a área e mostrando na animação
method = TrapezoidalRule()
integral = solve(problem, method)
integral = round(integral[1]; digits=3) #Arredonda.
integral = string(integral)
p = plot(x, prob,label=L"$|\Phi|^2$", legendfont=font(15), fill=true, fillalpha=0.2)
titulo = "Poço Infinito"*", "*", "*L"$\sigma=$"*string(sigma)*", "* L"$dt=$"*string(dt)* ", " *L"$t=$" * string(round(t[i], digits=3))*", Área="*integral
plot!(x,V, label="Potencial", legendfont=font(15))
plot!(title=titulo,
xlabel = "x",
xlim=(15,35),
xticksfont = font(13),
ticksfontsize = 10,
ylim=(0,0.6),
yticksfont=font(13),
)
i+=2 ##O passo é dado de 2 em 2 para deixar gif mais leve.
end
arquivo = "diracpoco.gif"
gif(anim, arquivo, fps=30)
end
main()
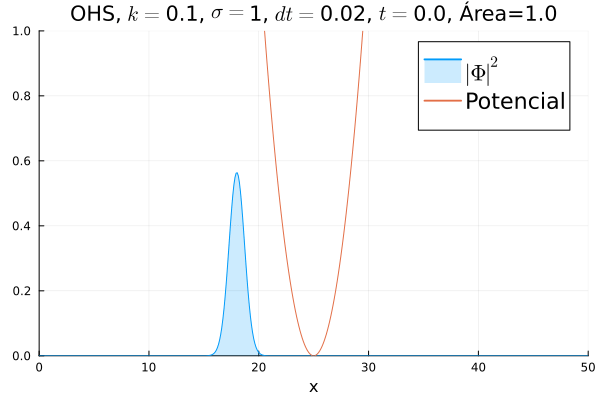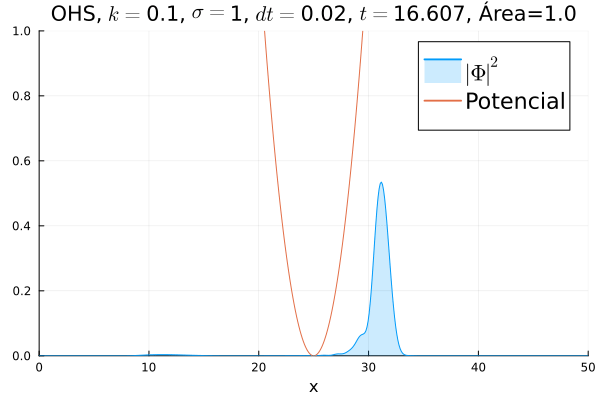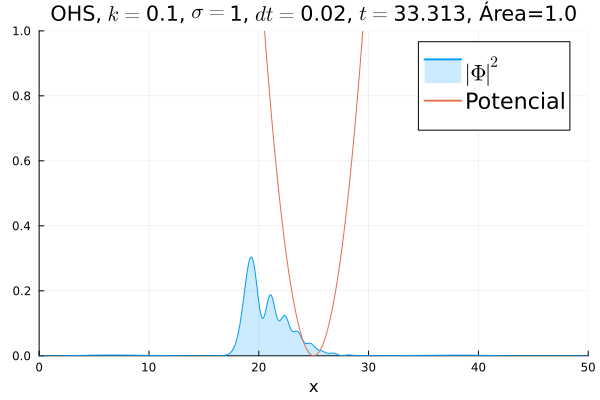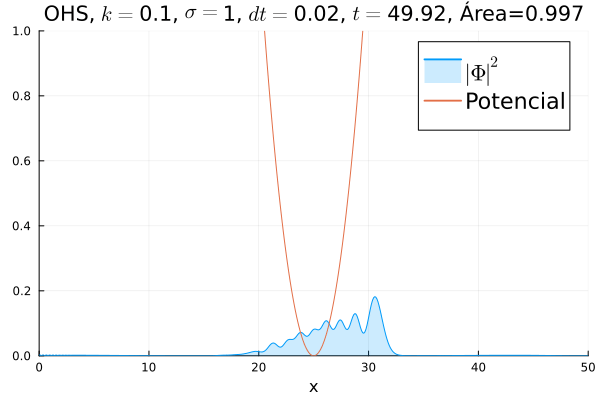
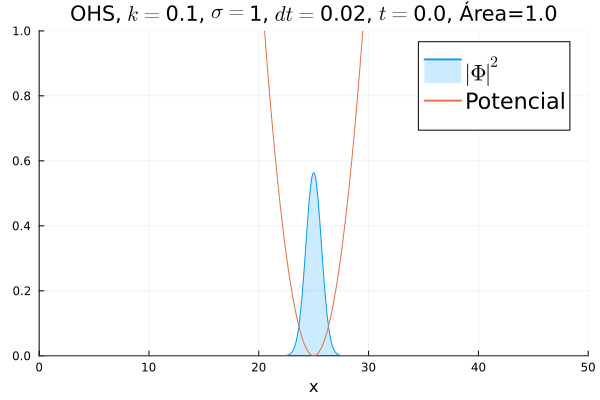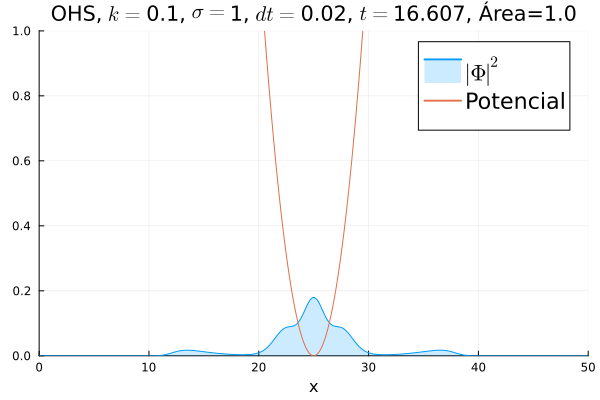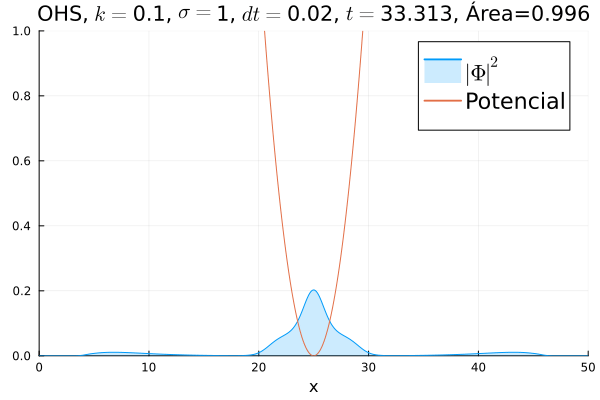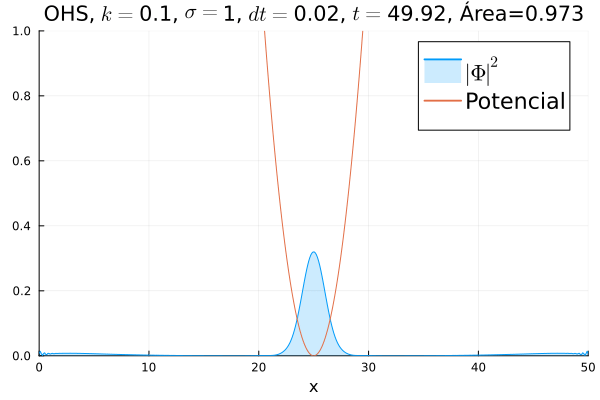
Oscilador Harmônico Simples
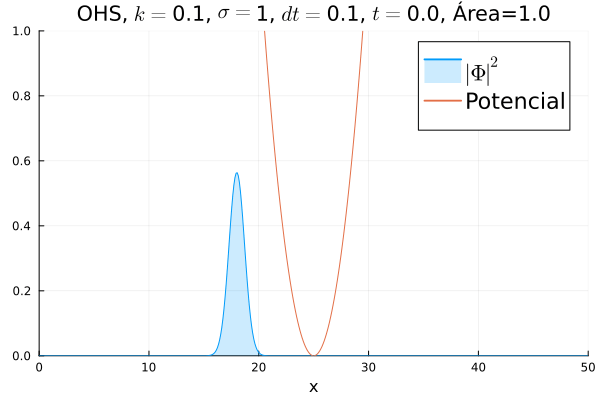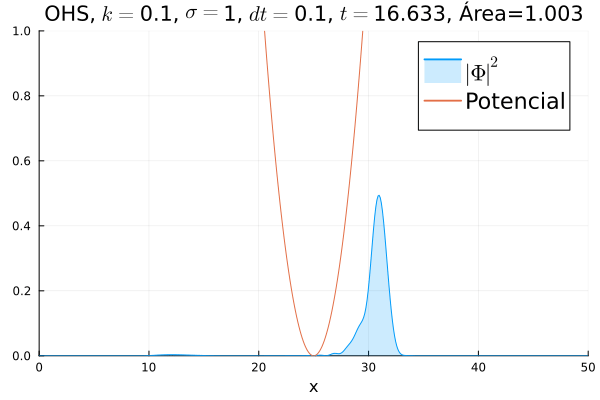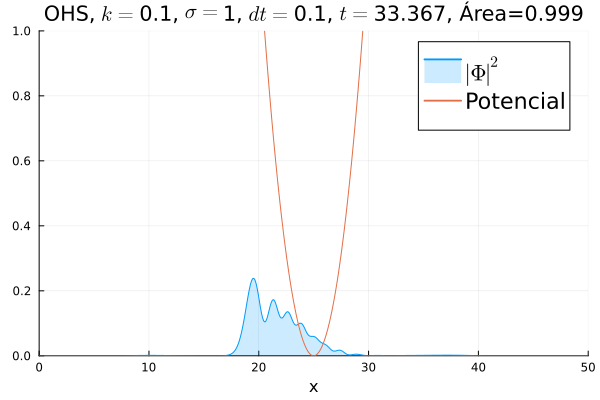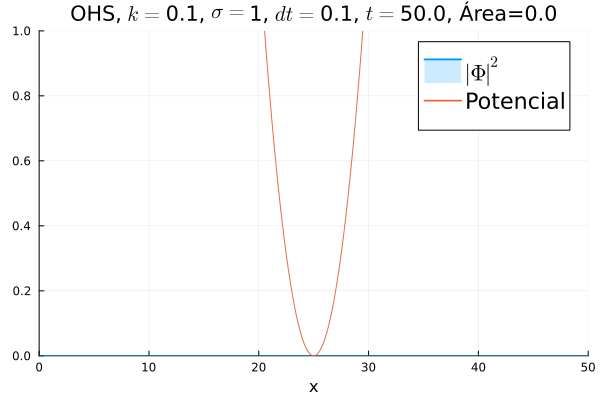
Inicialmente, realizou-se a simulação deslocando o pacote gaussiano para a posição inicial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=18} , com a finalidade de observar a oscilação. Testou-se a simulação com diferentes Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} 's; escolheu-se o que está mostrado abaixo pois facilita a visualização do comportamento oscilatório.
Nota-se um comportamento análogo ao caso clássico; porém, em alguns momentos é possível observar certos harmônicos do pacote de onda. Além disso, nota-se nas extremidades um valor máximo para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\mathbf{\Phi}|^2} , também condizente com o caso clássico.
Durante testes nas simulações, notou-se que a área sob a curva possui variações quando se utiliza um passo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta t} muito alto. Nesse caso, a convergência do método de Crank-Nicolson para os valores teóricos depende da malha utilizada, embora a estabilidade dele seja incondicional. A diferença pode ser vista comparando-se a animação abaixo com a anterior:
Em seguida, passou-se para uma condição inicial com um pacote gaussiano centralizado:
Mesmo que a posição inicial esteja no centro, devido ao fato da posição não estar bem definida ocorrem pequenas oscilações em torno do ponto de equilíbrio.
Por fim, segue o código utilizado para o oscilador harmônico simples (a diferença entre cada caso é só as constantes e a condição inicial).
function main()
L = 50 #Dimensão espacial matriz
k=0.1 #"Constante Elástica" do oscilador harmônico
sigma = 1 #Largura do pacote gaussiano
dt = 0.02
size= 10*L
h = L/size ##Passo espacial
tmax = 50
tsize = round(Int64, tmax/dt) #Tamanho do vetor tempo
t = LinRange(0, tmax, tsize)
x = LinRange(0, L, size)
V = zeros(size)
xi = init(LinRange(0, L, size), sigma) #Condição inicial pacote gaussiano
V = OHS(V,x,k) ##inicializa o potencial
f,g =CN(size,h,tsize, V, dt,xi)
i=1
#Faz o gif
anim = @animate while i<=tsize
f_real = real(f[i, :])
f_imag = imag(f[i, :])
g_real = real(g[i, :])
g_imag = imag(g[i, :])
probf = abs2.(f[i, :])
probg = abs2.(g[i, :])
prob = probf + probg
problem = SampledIntegralProblem(prob, x) ##Calcula a área sob a curva
method = TrapezoidalRule()
integral = solve(problem, method)
integral = round(integral[1]; digits=3)
integral = string(integral)
p = plot(x, prob,label=L"$|\Phi|^2$", legendfont=font(15), fill=true, fillalpha=0.2)
#=
p=plot(x, probf, label=L"$|\phi_1|^2$", legendfont=font(15))
plot!(x, probg, label=L"$|\phi_4|^2$", legendfont=font(15))
=#
titulo = "OHS"*", "*L"$k=$"*string(k)*", "*L"$\sigma=$"*string(sigma)*", "* L"$dt=$"*string(dt)* ", " *L"$t=$" * string(round(t[i], digits=3))*", Área="*integral
plot!(x,V, label="Potencial", legendfont=font(15))
plot!(title=titulo,
xlabel = "x",
xlim=(0,50),
xticksfont = font(13),
ticksfontsize = 10,
ylim=(0,1),
yticksfont=font(13),
)
i+=5 ##Feito de 5 em 5 para deixar .gif mais leve
end
arquivo = "diracOHS.gif"
gif(anim, arquivo, fps=30)
end
main()
Equação 1D com potencial "escalar"
Consideraremos agora o problema com o potencial "escalar" Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{sc}} . Dentro do formalismo da relatividade, os potenciais podem ser classificados de acordo com o seu comportamento frente a uma transformação de Poincaré: o potencial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} se transforma como um vetor (por isso chamado de potencial "vetor"), e o potencial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{sc}} , como um escalar (potencial "escalar"). Como exemplo de potencial do tipo vetor, temos os potenciais eletromagnéticos; e de potencial do tipo escalar, pode-se citar modelos de confinamento. Na prática, pode-se dizer que o potencial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{sc}} altera a massa de repouso "efetiva" da partícula. Para este assunto, deixamos (4) e (5) como referências.
Por ser um tópico bastante especializado, será considerado aqui apenas o caso do poço infinito. O problema é apenas uma extensão do que foi exposto nessa seção; a discretização e a estabilidade do método de Crank-Nicolson são análogas, bastando apenas fazer Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha^n = 1 + \frac{i \Delta t}{2}(V^n _j + V_{{sc}_j}^n + 1)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta^n = 1 + \frac{i \Delta t}{2}(V^n _j - V_{{sc}_j}^n -1)} .
Poço Infinito
Fez-se uma simulação completamente análoga à anterior, mas usando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=0} e definindo o poço infinito em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{sc}} . A animação está reproduzida abaixo.
Não há diferença notável com relação ao poço infinito em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} : o confinamento da partícula não muda, mesmo que a sua massa de repouso "efetiva" sim. No entanto, ressalta-se que esse é o comportamento conjunto das duas componentes Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_1} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_4} ; o comportamento individual de cada uma pode ser diferente.
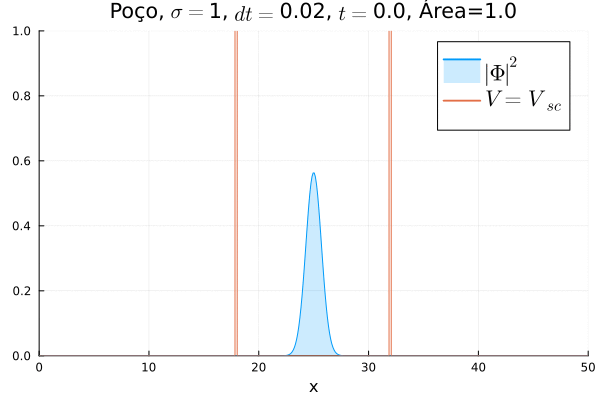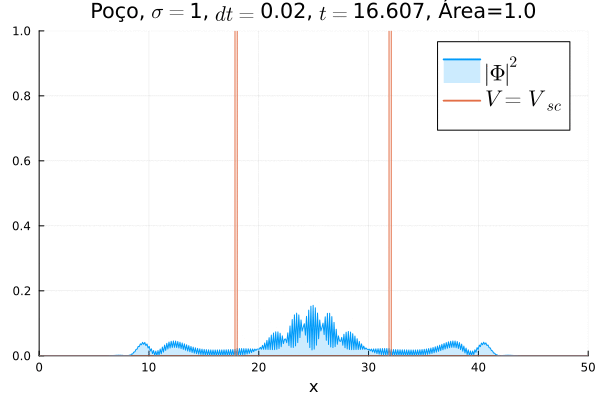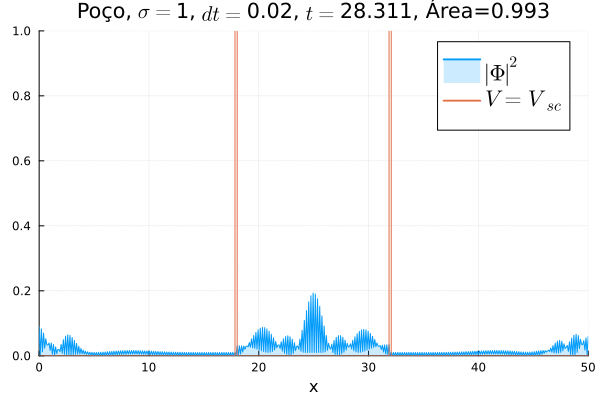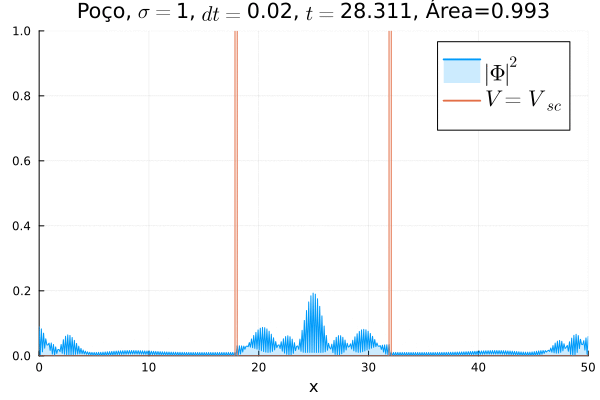
Em seguida, foi feita uma simulação colocando o poço infinito nos dois potenciais, ou seja, fazendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=V_{sc}}
, conforme animação abaixo.
Dessa vez, o comportamento é bastante diferente: a partícula fica apenas parcialmente confinada no poço, sendo parte da função de onda transmitida. Assim, observa-se um fenômeno que não ocorre na formulação não relativística da Mecânica Quântica: o de tunelamento em uma barreira infinita.
Segue abaixo o código utilizado para produzir as animações, adaptado do código utilizado aqui. A diferença entre as duas animações é de apenas uma linha, definindo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=0} ou Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=V_{sc}} .
using Plots
using LaTeXStrings
using LinearAlgebra
using Integrals
function init(x, sigma)
arg1 = @. ((-(x-25)^2)/(2*sigma^2))
arg2 = 1/sqrt(sqrt(pi)*sigma)
return arg2*exp.(arg1) ##Inicializo com um pacote gaussiano
end
function poco(V, h)
#Quero colocar nas posições 18 e 32
V[round(Int64, 18/h)] = 100000
V[round(Int64, 32/h)] = 100000
return V
end
##Matrizes do método de Crank-Nicholson
function matriz(dt,h,L, V, Sc)
A = Diagonal(ones(L).*(1 .+ im*dt*0.5.*(V+Sc.+1)))
B = LinearAlgebra.Tridiagonal(ones(L-1).*(-dt/(4*h)), zeros(L), ones(L-1).*(dt/(4*h)))
C = Diagonal(ones(L).*(1 .+ im*dt*0.5.*(V-Sc.-1)))
A = Array(A)
B = Array(B)
C = Array(C)
A_i = inv(A)
B_i = inv(B)
C_i = inv(C)
AiB = A_i*B
CiB = C_i*B
D = B_i*conj(A) + CiB
E = I(L) + C_i*conj(C)
F = B_i*A -CiB
G = A_i*conj(A) + I(L)
H = AiB + B_i*conj(C)
J = AiB - B_i*conj(C)
F_i = inv(F)
J_i = inv(J)
K = F_i*D
L = F_i*E
M = J_i*G
N = J_i*H
return K, L, M, N
end
function CN(size, h, tsize, V, Sc, dt, ci)
f = zeros(Complex, tsize, size) #Cada linha representa vetor posição em um tempo diferente. ## phi 1
g = zeros(Complex, tsize, size) ##phi 4
A, B, C, D = matriz(dt, h, size, V, Sc) #Matrizes do método Crank-Nicholson
f[1, :] = ci ##Condição Inicial
g[1, :] = zeros(size)
##Condições de Contorno
f[:, 1] = zeros(tsize)
f[:, end] = zeros(tsize)
g[:, 1] = zeros(tsize)
g[:, end] = zeros(tsize)
i=2 #Não interfiro nos contornos
while i<tsize
f[i, :] = A*f[i-1, :] - B*g[i-1, :]
g[i, :] = C*f[i-1, :] - D*g[i-1, :]
i+=1
end
return f, g
end
function main()
L = 50 #Dimensão espacial matriz
sigma = 1 #Largura do pacote gaussiano
dt = 0.02
size= 10*L
h = L/size ##Passo espacial
tmax = 50
tsize = round(Int64, tmax/dt) #Tamanho do vetor tempo
t = LinRange(0, tmax, tsize)
x = LinRange(0, L, size)
V = zeros(size)
Sc = copy(V)
xi = init(LinRange(0, L, size), sigma) #Condição inicial pacote gaussiano
Sc = poco(Sc,h) ##potencial "escalar"
V = copy(Sc) ##potencial "vetor"
f,g = CN(size,h,tsize,V,Sc,dt,xi)
i=1
#Faz o gif
anim = @animate while i<=tsize
f_real = real(f[i, :])
f_imag = imag(f[i, :])
g_real = real(g[i, :])
g_imag = imag(g[i, :])
probf = abs2.(f[i, :])
probg = abs2.(g[i, :])
prob = probf + probg
problem = SampledIntegralProblem(prob, x) ##Calcula a área sob a curva
method = TrapezoidalRule()
integral = solve(problem, method)
integral = round(integral[1]; digits=3)
integral = string(integral)
p = plot(x, prob,label=L"$|\Phi|^2$", legendfont=font(15), fill=true, fillalpha=0.2)
titulo = "Poço"*", "*L"$\sigma=$"*string(sigma)*", "* L"$dt=$"*string(dt)* ", " *L"$t=$" * string(round(t[i], digits=3))*", Área="*integral
plot!(x,Sc, label=L"$V=V_{sc}$", legendfont=font(15))
plot!(title=titulo,
xlabel = "x",
xlim=(0,50),
xticksfont = font(13),
ticksfontsize = 10,
ylim=(0,1),
yticksfont=font(13),
)
i+=5 ##Feito de 5 em 5 para deixar .gif mais leve
end
arquivo = "diracVscVPoco.gif"
gif(anim, arquivo, fps=30)
end
main()
Equação 2D
Passamos agora para o estudo da equação de Dirac em duas dimensões. Para tanto, a equação foi integrada utilizando-se o método de Leap-Frog, tanto com um potencial coulombiano central como com um potencial cossenoide. Em ambos casos, o potencial não depende do tempo e a condição inicial constituiu-se de um pacote gaussiano, centralizado em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (0,0)} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_1} e em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1,1)} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_4} .
O procedimento adotado segue o utilizado em (3). De forma aproximada, atribuiu-se para o passo temporal Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=1} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\Phi}_{i,j}^{1}=\mathbf{\Phi}_{i,j}^{0} -\sin \left(\frac{\Delta t }{\varepsilon} \right)\sigma_1(\delta_x+\delta_y)\mathbf{\Phi}_{i,j}^{0}-i \left(\sin\left(\frac{\Delta t }{\varepsilon^2}\right)\sigma_3+\Delta t V_{i,j}^{0} I_2\right)\mathbf{\Phi}_{i,j}^{0} }
Segue abaixo o código utilizado para ambos potenciais, onde seu uso difere apenas em qual potencial foi comentado. A escolha do parâmetro de escala foi Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon = 0.8} .
using Plots
using LinearAlgebra
using LaTeXStrings
using Printf
function initial_values()
L=10 #Malha de 4*(L/h)² de -L a L nas duas dimensões
h=1/16 #dx,dy=h
dt=0.01
ep=0.8 #0<ep<=1 -> := v/c
tmax=8.
x=LinRange(-L,L,2*Int(L/h))
y=LinRange(-L,L,2*Int(L/h))
#Potencial Coulombiano
V= zeros(ComplexF64,2*Int(L/h),2*Int(L/h))
Qe=1.
K=1 #K=9*10^9
V = [ -K*Qe/sqrt((x[i]^2 + y[j]^2)) for i in 1:2*Int(L/h), j in 1:2*Int(L/h) ]
#Potencial Cossenoide
#V = [ cos((-4*pi/sqrt(3))*x[i])+cos((2*pi/sqrt(3))*x[i]+2*pi*y[j])+cos((2*pi/sqrt(3))*x[i]-2*pi*y[j]) for i in 1:2*Int(L/h), j in 1:2*Int(L/h) ]
#psi 1 inicial (t=0)
psi1 =zeros(ComplexF64,2*Int(L/h),2*Int(L/h))
psi1 = [ (exp(-((x[i])^2+(y[j])^2)/2)) for i in 1:2*Int(L/h), j in 1:2*Int(L/h) ]
#psi4 iniciall (t=0)
psi4 =zeros(ComplexF64,2*Int(L/h),2*Int(L/h))
psi4 = [ exp(-((x[i] -1 )^2+(y[j] -1)^2)/2) for i in 1:2*Int(L/h), j in 1:2*Int(L/h) ]
#próximo psi1 (t=0+dt)
nextpsi1 =zeros(ComplexF64,2*Int(L/h),2*Int(L/h))
j=2
while j < 2*Int(L/h)
i=2
while i < 2*Int(L/h)
nextpsi1[i,j] = psi1[i,j]-sin(dt/ep)*((psi4[i+1,j]-psi4[i-1,j]) + (psi4[i,j+1]-psi4[i,j-1]))/(2*h)-im*(-im*sin(dt/(ep^2))*psi4[i,j]+h*V[i,j]*psi1[i,j])
i+=1
end
j+=1
end
#próximo psi4 (t=0+dt)
nextpsi4 =zeros(ComplexF64,2*Int(L/h),2*Int(L/h))
j=2
while j < 2*Int(L/h)
i=2
while i < 2*Int(L/h)
nextpsi4[i,j]= psi4[i,j]-sin(dt/ep)*((psi1[i+1,j]-psi1[i-1,j]) + (psi1[i,j+1]-psi1[i,j-1]))/(2*h)-im*(im*sin(dt/(ep^2))*psi1[i,j]+h*V[i,j]*psi4[i,j])
i+=1
end
j+=1
end
return L,h,dt,ep,tmax,x,y,V,psi1,psi4,nextpsi1,nextpsi4
end
L,h,dt,ep,tmax,x,y,V,psi1,psi4,nextpsi1,nextpsi4=initial_values()
#listas para salvar os frames do gif
anim_psi1=[]
anim_psi4=[]
#cópia para manipulação
uu=deepcopy(psi1)
vv=deepcopy(psi4)
t=0;
while t < tmax
global j
global uu; global vv;
global u; global v;
u=deepcopy(nextpsi1)
v=deepcopy(nextpsi4)
j=2
while j < 2*Int(L/h)
global i=2
while i < 2*Int(L/h)
global i
nextpsi1[i,j]= -(dt/(ep*h))*(v[i+1,j]-v[i-1,j])+((im*dt)/(ep*h))*(v[i,j+1]-v[i,j-1])-((2*im*dt)/(ep^2))*u[i,j]-(2*dt*im)*V[i,j]*u[i,j]+uu[i,j]
nextpsi4[i,j]= -(dt/(ep*h))*(u[i+1,j]-u[i-1,j])-((im*dt)/(ep*h))*(u[i,j+1]-u[i,j-1])+((2*im*dt)/(ep^2))*v[i,j]+(2*dt*im)*V[i,j]*v[i,j]+vv[i,j]
i+=1
end
j+=1
end
uu=deepcopy(u)
vv=deepcopy(v)
global t+=dt
push!(anim_psi1,deepcopy(nextpsi1))
push!(anim_psi4,deepcopy(nextpsi4))
end
#montagem do gif
function psi_anim(x,y,psi1,psi4,tmax)
i=1
anim = @animate while i<=length(psi1)
prob = abs2.(psi1[i])+abs2.(psi4[i])
t=0.01*i
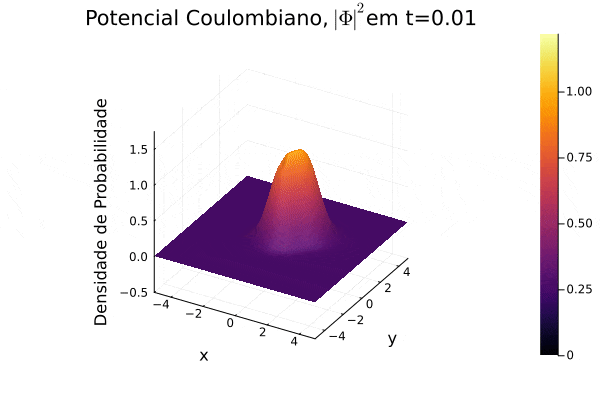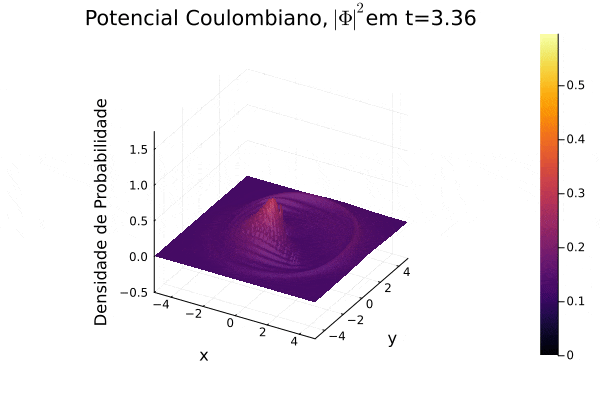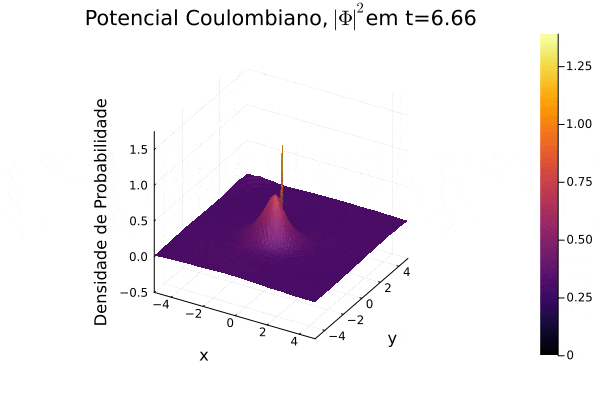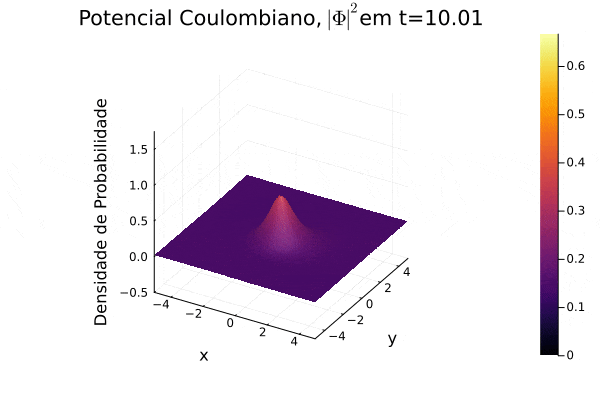
titulo="Potencial Coulombiano, "*L"| \Phi |^{2}"*@sprintf("em t=%0.2f",t)
#titulo=@sprintf("| \Phi |^{2}em t = %f",
u=2*L/h #exibe a malha de forma reduzida
p = surface(x[Int(u/4):Int(3*u/4)],y[Int(u/4):Int(3*u/4)],prob[Int(u/4):Int(3*u/4),Int(u/4):Int(3*u/4)],title=titulo, xlabel = "x",ylabel="y",zlabel="Densidade de Probabilidade" ,zlim=(-0.5,1.75),clim=(0, maximum(prob)))
i+=5
end
arquivo = "psi_coulomb.gif"
gif(anim, arquivo, fps=15)
end
psi_anim(x,y,anim_psi1,anim_psi4,tmax)
Potencial Coulombiano
Na animação gerada, nota-se a dispersão para o infinito no momento inicial e o movimento semelhante a uma órbita que a curva de densidade de probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\mathbf{\Phi}|^2} realiza em torno do centro do sistema de coordenadas, pois o potencial escolhido varia radialmente de forma positiva. Observa-se um padrão de ruído na parte central, o qual não foi estudado a fundo, mas, nesse caso, é exclusivo de pontos próximos ao ponto de divergência da função potencial.
Potencial Cossenoide
Reproduziu-se o potencial estudado em (3), onde recebe o nome de "honeycomb potential". Observa-se, no período de tempo exibido, o espalhamento da função potencial no plano cartesiano e que a função densidade de probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\mathbf{\Phi}|^2} forma um contorno de curva que se assemelha um favo de mel.
Referências
- DIRAC, P. A. M. The quantum theory of the electron. Proceedings of the Royal Society of London A, v. 117, n. 778, p. 610–624, fev. 1928.
- SAKURAI, J. J. Mecânica quântica moderna. 2. ed. Porto Alegre: Bookman, 2012.
- BAO, W. et al. Numerical Methods and Comparison for the Dirac Equation in the Nonrelativistic Limit Regime. Journal of Scientific Computing, v. 71, n. 3, p. 1094–1134, jun. 2017.
- SOFF, G. et al. Solution of the Dirac Equation for Scalar Potentials and its Implications in Atomic Physics. Zeitschrift für Naturforschung A, v. 28, n. 9, p. 1389–1396, 1 set. 1973.
- THALLER, B. The Dirac equation. Berlin: Springer, 2010.




































![{\displaystyle i\hbar {\frac {\partial }{\partial t}}\Psi =H\Psi \to \left[iI_{4}{\frac {\partial }{\partial t}}-H\right]\Psi =0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a47cd71f320c16b7c19d774e965a50d7a9ffe74c)







![{\displaystyle i\partial _{t}\mathbf {\Phi } =[-i\sigma _{1}\partial _{x}+\sigma _{3}]\mathbf {\Phi } +[V(t,x)I_{2}]\mathbf {\Phi } }](https://wikimedia.org/api/rest_v1/media/math/render/svg/856d45f8bb00f22f263d8cb7b4beaa0994aca01b)

















![{\displaystyle i\delta _{t}\mathbf {\Phi _{j}^{n}} =[-i\sigma _{1}\delta _{x}+\sigma _{3}]\mathbf {\Phi _{j}^{n}} +[V_{j}^{n}I_{2}]\mathbf {\Phi _{j}^{n}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/066376632627056eca4aa2be571668af4d36d9ae)
![{\displaystyle i{\frac {\mathbf {\Phi _{j}^{n+1}} -\mathbf {\Phi _{j}^{n}} }{\Delta t}}=[-i\sigma _{1}\delta _{x}+\sigma _{3}]\mathbf {\Phi _{j}^{n}} +[V_{j}^{n}I_{2}]\mathbf {\Phi _{j}^{n}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7446ce3f82727c2b53fa903abb6796149e3ae1b4)
![{\displaystyle i\mathbf {\Phi _{j}^{n+1}} =\mathbf {\Phi _{j}^{n}} +\Delta t[-i\sigma _{1}\delta _{x}+\sigma _{3}]\mathbf {\Phi _{j}^{n}} +\Delta t[V_{j}^{n}I_{2}]\mathbf {\Phi _{j}^{n}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab7fbc7e09a9758938eb89013fe5030a54e5abc1)




![{\displaystyle i\mathbf {\Phi _{j}^{n+1}} =\mathbf {\Phi _{j}^{n}} +\Delta t[-i\sigma _{1}\delta _{x}+\sigma _{3}]\mathbf {\Phi _{j}^{n+1}} +\Delta t[V_{j}^{n+1}I_{2}]\mathbf {\Phi _{j}^{n+1}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/315ca5c2ae8c8d289445d2fad96a783defa76791)



![{\displaystyle i\delta _{t}\mathbf {\Phi _{j}^{n}} =[-i\sigma _{1}\delta _{x}+\sigma _{3}]\mathbf {\Phi _{j}^{n+1/2}} +[V_{j}^{n+1/2}I_{2}]\mathbf {\Phi _{j}^{n+1/2}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/31e9be8f4009379093880a6419a1bfc7236ab22d)


![{\displaystyle i{\frac {\mathbf {\Phi _{j}^{n+1}} -\mathbf {\Phi _{j}^{n}} }{\Delta t}}=-{\frac {i}{2}}\sigma _{1}\left[{\frac {\mathbf {\Phi _{j+1}^{n+1}} -\mathbf {\Phi _{j-1}^{n+1}} }{2h}}+{\frac {\mathbf {\Phi _{j+1}^{n}} -\mathbf {\Phi _{j-1}^{n}} }{2h}}\right]+\sigma _{3}\left({\frac {\mathbf {\Phi _{j}^{n+1}} +\mathbf {\Phi _{j}^{n}} }{2}}\right)+I_{2}\left({\frac {V_{j}^{n+1}\mathbf {\Phi _{j}^{n+1}} +V_{j}^{n}\mathbf {\Phi _{j}^{n}} }{2}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36c63cac7e0404678553d9417eff8e3740d63a6e)
![{\displaystyle \left[I_{2}-{\frac {i}{2}}\Delta t\sigma _{3}-{\frac {i}{2}}\Delta tV_{j}^{n}I_{2}\right]\mathbf {\Phi _{j}^{n}} -{\frac {\Delta t}{4h}}\sigma _{1}\left[\mathbf {\Phi _{j+1}^{n}} -\mathbf {\Phi _{j-1}^{n}} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8730f3d4a62979df98a9dba9c63c334ea822a579)