Equações de Lotka-Volterra Estocásticas

Grupo: André Luis Della Valentina, Lucas dos Santos Assmann, Vinícius Bayne Müller

Introdução

O modelo de Lotka-Volterra foi desenvolvido originalmente na década de 1920, de maneira independente por Vito Volterra e Alfred Lotka, e é utilizado para descrever a dinâmica de populações com relações de predatismo. Em sua forma mais simples, as equações de Lotka-Volterra podem ser escritas como

${\begin{cases}{\dot {x}}=x(a-by)\\{\dot {y}}=y(-c+fx)\end{cases}}$

onde $x$ e $y$ denotam, respectivamente, a densidade populacional de presas e de predadores, e $a$, $b$, $c$ e $f$ são constantes positivas.

Pode-se interpretar os parâmetros da seguinte maneira:

• $a$: taxa de crescimento livre da presa;
• $b$: taxa de predação;
• $c$: taxa de mortalidade livre do predador;
• $f$: taxa de crescimento do predador devido à predação.

É interessante notar que o sistema apresenta um ponto fixo não trivial em $(x^{\ast },y^{\ast })=\left({\frac {c}{f}},{\frac {a}{b}}\right)$. Pode-se mostrar também que as demais soluções (além da trivial) são órbitas fechadas no espaço de fase.

Nesse modelo simples, não há competição entre indivíduos de uma mesma espécie e não há limite ecológico para o sustento das populações; ou seja, a população de presas cresce exponencialmente na ausência de predadores. A fim de tornar esse modelo mais realista, pretendemos estudar versões estocásticas do mesmo, que podem ser construídas de diferentes maneiras, e analisar o efeito do ruído sobre o comportamento dinâmico.

Modelo estocástico

Buscamos construir um modelo estocástico de Lotka-Volterra utilizando um processo de Wiener; contudo, a adição de ruído branco nas equações diferenciais pode ser feita de várias maneiras. Consideraremos, aqui, duas delas: ruído adicionado nos parâmetros e ruído externo ao sistema.

Ruído externo

Como primeiro modelo, simplesmente adicionaremos um ruído externo nas equações diferenciais. Esse ruído pode ser interpretado como fatores ambientais independentes das populações, causando tanto benefícios (abundância de alimento, condições climáticas favoráveis para reprodução etc.) como prejuízos (escassez, condições climáticas desfavoráveis etc.). Como as equações tratam de densidades populacionais, devemos utilizar um ruído _multiplicativo_, pois os efeitos dos fatores externos sentidos pelas populações devem ser proporcionais ao tamanho dela. Assim, escrevemos o modelo como

${\begin{cases}{\dot {X}}=X(a-bY)+\epsilon _{x}\xi _{x}X\\{\dot {Y}}=Y(-c+fX)+\epsilon _{y}\xi _{y}Y\end{cases}}$

onde os $\xi _{i}$ são os ruídos brancos de cada variável, e $\epsilon _{i}$, a intensidade dos mesmos.

Ao escrever o diferencial total, obtemos

${\begin{cases}dX=X(a-bY)dt+\epsilon _{x}X\bullet dW_{x}\\dY=Y(-c+fX)dt+\epsilon _{y}Y\bullet dW_{y}\end{cases}}$

Itô

Transformando as equações acima para equações diferenciais estocásticas no sentido de Itô, obtemos

${\begin{cases}dX=X(a-bY+{\frac {1}{2}}{\epsilon _{x}}^{2})dt+\epsilon _{x}XdW_{x}\\dY=Y(-c+fX+{\frac {1}{2}}{\epsilon _{y}}^{2})dt+\epsilon _{y}YdW_{y}\\\end{cases}}$

Observa-se que, além de um incremento de Wiener proporcional a $X$ e $Y$, obtém-se parâmetros determinísticos "efetivos" $a\to a+{\frac {1}{2}}{\epsilon _{x}}^{2}$ e $c\to c-{\frac {1}{2}}{\epsilon _{y}}^{2}$.

Ruído nos parâmetros

Analisaremos o modelo proposto no sentido de Itô e no sentido de Stratonovich.

Itô

Uma outra maneira de explorar o ruído nas equações de Lotka-Volterra é substituir o ruído de tal maneira que $a\to a+{\epsilon _{x}}X\xi _{x}(t)$ e $c\to c+{\epsilon _{y}}Y\xi _{y}(t)$, onde $\epsilon _{x}$ e $\epsilon _{y}$ são constantes e $\xi _{i}(t)$ é o ruído branco definido pelo processo de Wiener. O que modelaria um sistema que relaciona as populações entre dois níveis vizinhos da cadeia alimentar, abrangendo uma biodiversidade representada por parâmetros efetivos estocásticos nas taxas $a$ e $c$ proporcional ao número de presas e predadores, ou seja, há uma diversidade de taxas de reprodutibilidade das presas e mortalidades dos predadores, o que representaria diversas populações de especíes diferentes. Dessa maneira, obtém-se a seguinte equação diferencial:

${\begin{cases}{\dot {X}}=X(a-bY)+\epsilon _{x}\xi _{x}(t)X^{2}\\{\dot {Y}}=Y(-c+fX)-\epsilon _{y}\xi _{y}(t)Y^{2}\end{cases}}$

Seja $A_{x}(X(t),Y(t))=X(a-bY)$, $A_{y}(X(t),Y(t))=Y(-c+fX)$, $B_{x}(X(t))=\epsilon _{x}X^{2}$ e $B_{y}(Y(t))=\epsilon _{x}Y^{2}$. Integra-se essa equação em ambos os lados de tal forma que:

${\begin{cases}\int _{t}^{t+\Delta t}{dX}=\int _{t}^{t+\Delta t}{X(a-bY)dt'}+\epsilon _{x}\int _{t}^{t+\Delta t}{X^{2}\xi _{x}(t')dt'}\\\int _{t}^{t+\Delta t}{dY}=\int _{t}^{t+\Delta t}{Y(-c+fX)dt'}+\epsilon _{y}\int _{t}^{t+\Delta t}{Y^{2}\xi _{y}(t')dt'}\end{cases}}$

A parte determinista é integrada trivialmente, porém para integrar o segundo termo das equações é necessário aproximar $B_{x}(X(t))\to B_{x}\left(X+{\frac {1}{2}}\Delta X\right)$ no intervalo $\Delta t$, e o mesmo para $B_{y}(Y(t))$. Expande-se $B_{i}$ em série de Taylor, conforme o cálculo de Itô, e então obtém-se as equações diferenciais estocásticas ao tomar o limite $\Delta t\to dt$:

${\begin{cases}dX=X(a-bY+{\epsilon _{x}}^{2}X^{2})dt+\epsilon _{x}X^{2}\bullet dW_{x}\\dY=Y(-c+fX+{\epsilon _{y}}^{2}Y^{2})dt-\epsilon _{y}Y^{2}\bullet dW_{y}\\\end{cases}}$

Ao integrá-las de $t$ a $t+\Delta t$ obtém-se o método numérico utilizado para fazer as simulações computacionais. Nota-se que a integral dos segundos termos são aproximadas para $B_{i}\Delta W_{i}$ no intervalo $\Delta t$. Então, é utilizado o método de Heun para integrar a parte determinística da equação, obtendo portanto o seguinte método:

${\begin{cases}X_{n+1}=X_{n}+{\frac {1}{2}}(k_{1x}+k_{2x})\Delta t+\epsilon _{x}X_{n}^{2}\Delta W_{x}\\Y_{n+1}=Y_{n}+{\frac {1}{2}}(k_{1y}+k_{2y})\Delta t-\epsilon _{y}Y_{n}^{2}\Delta W_{y}\\\end{cases}}$

onde

${\begin{cases}k_{1x}=X_{n}(a-bY_{n}+{\epsilon _{x}}^{2}X_{n}^{2})\\k_{2x}=(X_{n}+k_{1x}\Delta t)(a-b(Y_{n}+k_{1y}\Delta t)+{\epsilon _{x}}^{2}(X_{n}+k_{1x}\Delta t)^{2})\\k_{1y}=Y_{n}(-c+dX_{n}+{\epsilon _{y}}^{2}Y_{n}^{2})\\k_{2x}=(Y_{n}+k_{1y}\Delta t)(-c+d(X_{n}+k_{1x}\Delta t)+{\epsilon _{y}}^{2}(Y_{n}+k_{1y}\Delta t)^{2})\\\end{cases}}$

O índice $n$ representa o passo $\Delta t$ na iteração do método.

Stratonovich

O ruído pode ser adicionado nos parâmetros $b$ e $d$, de forma que $b\to b+\epsilon _{x}\xi _{x}(t))$ e $d\to d+\epsilon _{y}\xi _{y}(t))$, onde o ruído segue a forma de Stratonovich. Essa mudança pode ser interpretada como a predação de predadores de um mesmo nicho ecológico sobre uma presa, considerando que não há competição entre as diferentes espécies. Por outro lado, pode ser pensado como uma variação do efeito da caça sobre a população de um mesmo predador. Dessa forma, a dinâmica populacional se comporta como:

${\begin{cases}{\dot {X}}=X(a-bY)-\epsilon _{x}XY\xi _{x}(t)\\{\dot {Y}}=Y(-c+fX)+\epsilon _{y}XY\xi _{y}(t)\end{cases}}$

onde $\xi (t)$ é um ruído branco e $\epsilon >=0$. Considerando que $\bullet$ denota a integral de Stratonovich e $W_{n}(t)$ um escalar oriundo de processos de Wigner independentes, utiliza-se para aplicação no método numérico a seguinte equação diferencial estocástica:

${\begin{cases}{\dot {X}}=X(a-bY)dt-\epsilon _{x}XY\bullet dW_{x}\\{\dot {Y}}=Y(-c+fX)dt+\epsilon _{y}XY\bullet dW_{y}\end{cases}}$

Utilizando o método de Heun têm-se:

${\begin{cases}X_{n+1}=X_{n}+{\frac {1}{2}}(A(x_{n})+A(X_{1}))\Delta t+{\frac {1}{2}}\Delta W_{x}(B(x_{n})+B(X_{1}))\\Y_{n+1}=Y_{n}+{\frac {1}{2}}(A(y_{n})+A(Y_{1}))\Delta t+{\frac {1}{2}}\Delta W_{y}(B(y_{n})+B(Y_{1}))\\\end{cases}}$

onde

${\begin{cases}A(x_{n})=x_{n}(a-by_{n})\\A(y_{n})=y_{n}(-c+fx_{n})\\\\B(x_{n})=\epsilon _{x}x_{n}y_{n}\\B(y_{n})=-\epsilon _{y}x_{n}y_{n}\\\\X_{1}=x_{n}+{\sqrt {\Delta t}}A(x_{n})+\Delta W_{n}B(x_{n})\\Y_{1}=y_{n}+{\sqrt {\Delta t}}A(y_{n})+\Delta W_{n}B(y_{n})\\\\A(X_{1})=X_{1}(a-bY_{1})\\A(Y_{1})=Y_{1}(-c+fX_{1})\\\\B(X_{1})=\epsilon _{x}X_{1}Y_{1}\\B(Y_{1})=-\epsilon _{y}X_{1}Y_{1}\\\end{cases}}$

Código

A estrutura do código foi a mesma para os três casos considerados, mudando apenas os detalhes da equação diferencial utilizada. A integração numérica da parte determinística foi feita pelo Método de Heun. Todas as análises foram realizadas a partir de um número N de realizações independentes e então calcula-se a média e/ou variância para cada passo de tempo destas realizações. Podendo analisar fielmente as tendências do sistema estatisticamente.

Resultados

Nesta seção, abordará-se-a diversos aspectos sobre o comportamento numérico dos sistemas simulados. Avalia-se qualitativamente estabilidade e o comportamento do sistema conforme variação dos parâmetros a, b, c, f, condições iniciais e também da intensidade do ruído.

Ruído nos parâmetros

Itô

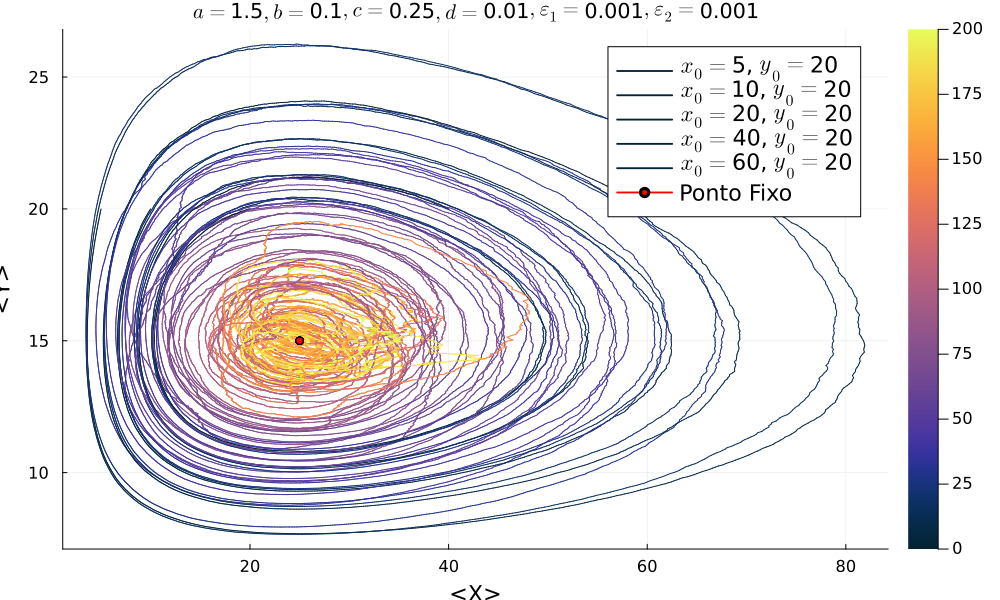
Primeiramente realizou-se simulações variando o número de presas iniciais para um número fixo de predadores, representando-o em um mapa de fase da média de 50 realizações:

Nota-se um comportamento característico de atratores, onde o ponto fixo das equações de Lotka-Volterra determinística é o mesmo (ponto vermelho). Evidencia-se que esse ponto fixo não depende das condições iniciais.

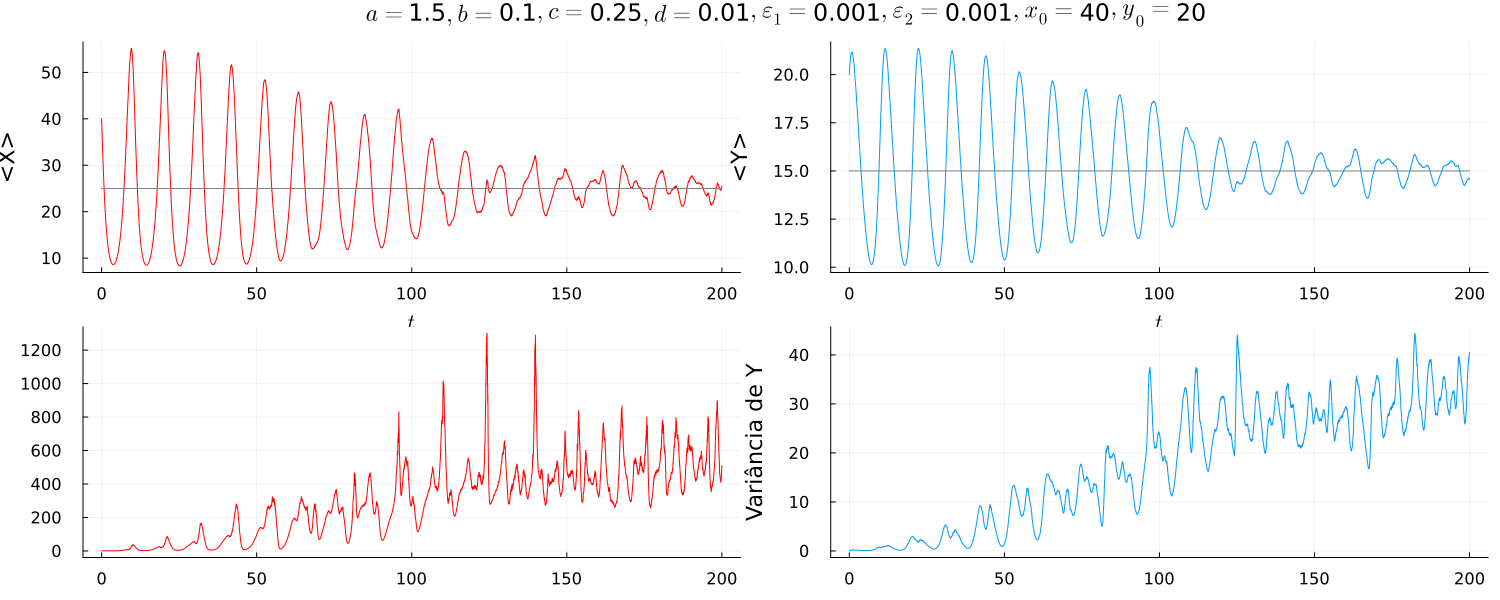
O comportamento atrativo fica claro ao analisar a média e a variância em função do tempo:

As amplitudes para os predadores e as presas diminuem conforme o tempo, porém nota-se que o ruído passa a se tornar mais evidente quando as amplitudes das órbitas são menores.

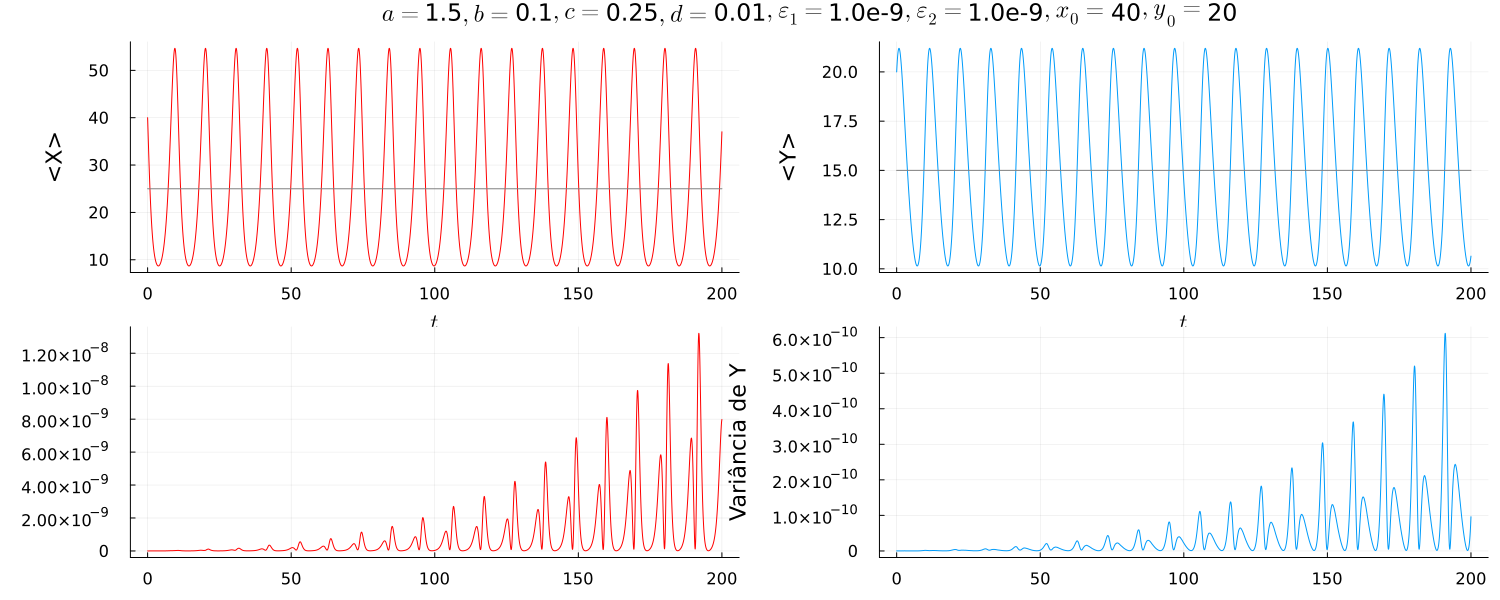
Com a finalidade de testar a coerência do sistema com o determinístico, integrou-se as equações para um ruído da ordem de $10^{-9}$.

Mostrando, portanto, que o sistema estocástico se reduz ao determinístico no limite em que o ruído é muito pequeno, dado que observa-se órbitas fechadas. Espera-se que a variância seja nula em um sistema determinístico, porém numericamente obteve-se oscilações que são da ordem do ruído ou menor, corroborando para a convergência do sistema estocástico para o determinístico para pequenos ruídos.

Ao realizar as simulações notou-se que o sistema é bastante sensível ao ruído, convergindo para valores bem estritos para os parâmetros, ruído e condição inicial. Mostrando, portanto, que embora esse sistema modele uma interação entre dois níveis da cadeia alimentar, ele possui alguns graves problemas, como a fácil divergência, devido, provavelmente, aos termos cúbicos das equações. Porém também houve resultados interessantes como os atratores, que podem representar uma espécie de equilíbrio ecológico, onde não há extinções com o passar do tempo. Um dos problemas mais sérios com relação ao modelo é que mesmo na ausência de presas a população de predadores pode crescer indefinidamente, o que não condiz com a realidade.

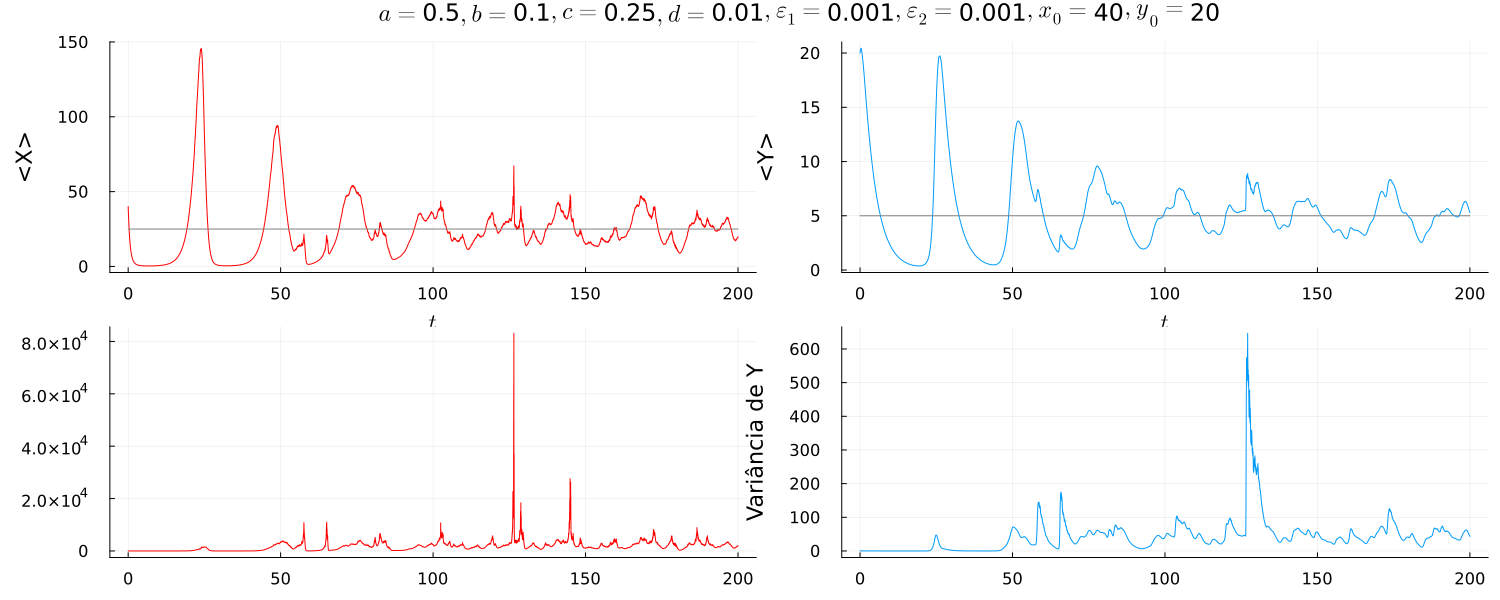
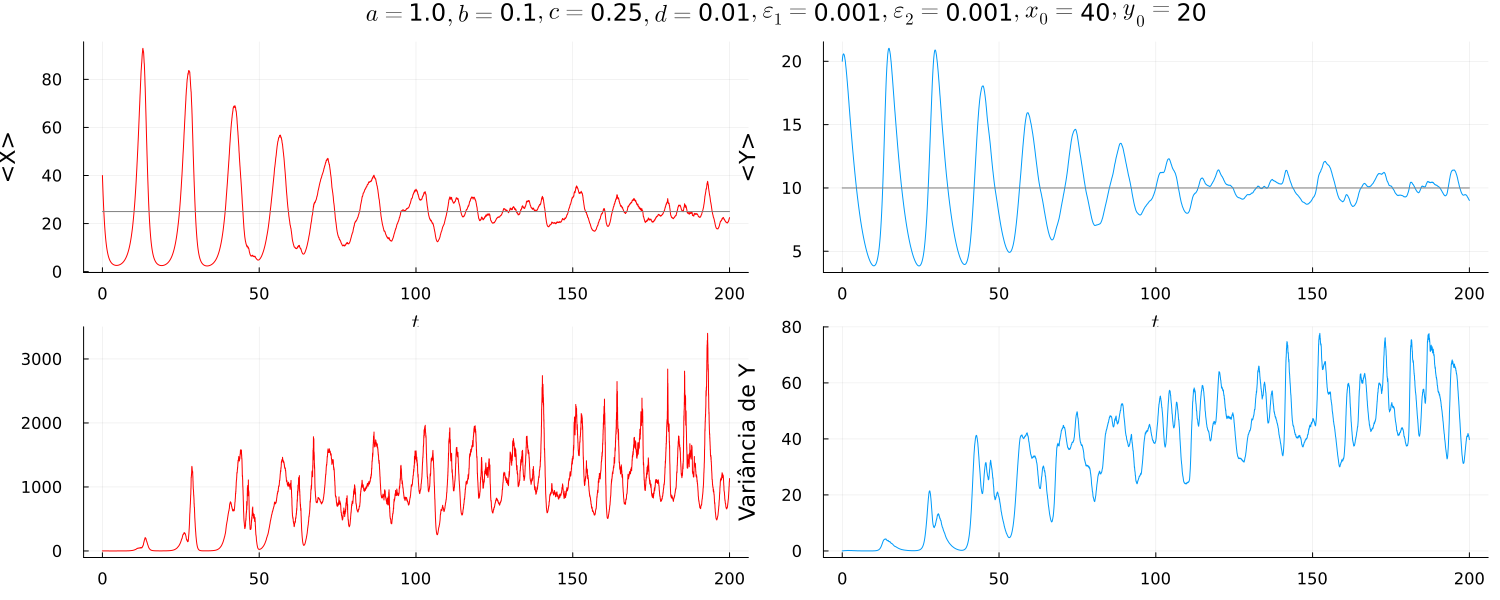
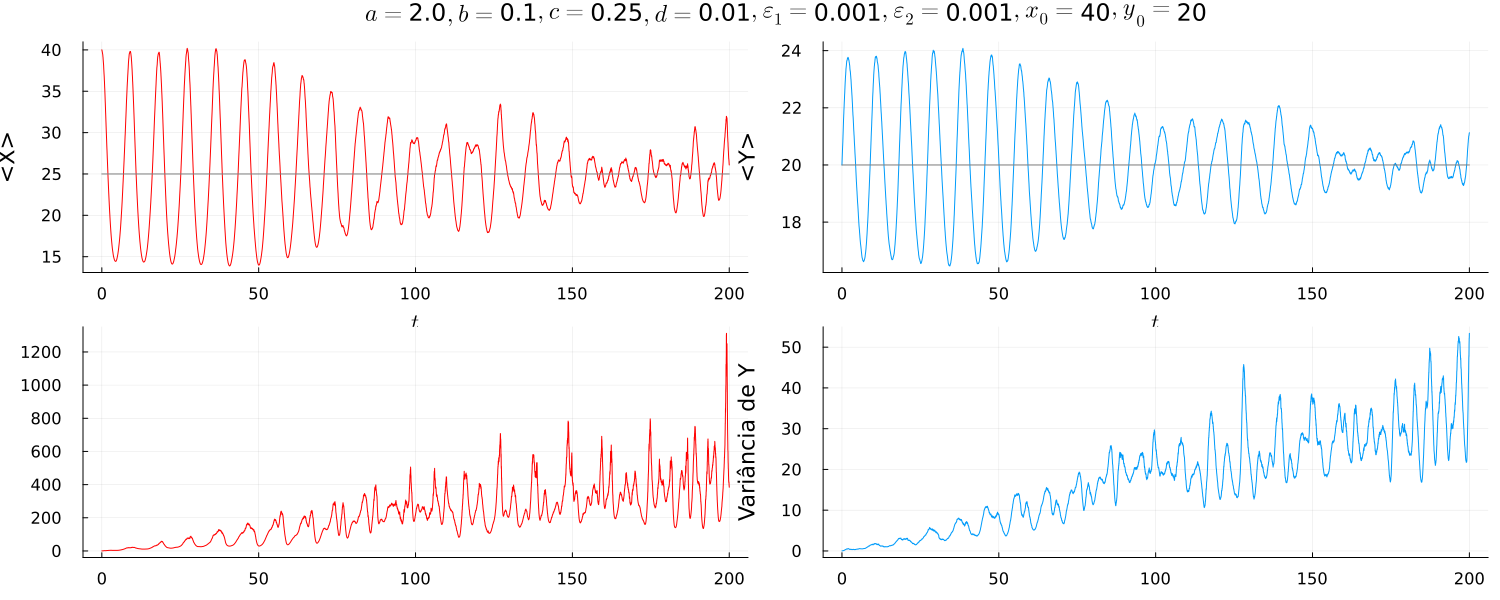
As simulações realizadas variando os parâmetros trouxeram pequenas modificações no comportamento do sistema, como a alteração do período, a quantidade de órbitas bem definidas e suas amplitudes.

Nota-se que os períodos vão diminuindo conforme $a$ aumenta enquanto as amplitudes tendem a diminuir. Os ruídos se tornaram mais presentes com grandes variâncias nas simulações com $a$ pequenos. Outra tendência observada foi de que o regime ruídoso parece ocorrer mais tarde para valores de $a$ maiores. O que provavelmente está associado com o fato de o ruído se tornar mais presente para pequenas oscilações temporais do número de presas, o que ocorre na região próxima do ponto fixo.

Referências

1. BRAUER, F.; CASTILLO-CHAVEZ, C. Mathematical Models in Population Biology and Epidemiology. New York, NY: Springer New York, 2012. v. 40
2. COELHO, P. J. de O. Equações de Lotka–Volterra Estocásticas: Simulações com o Matlab. 25 de junho de 2015. Disponível em https://www.academia.edu/52185574/Sistema_de_competi%C3%A7%C3%A3o_Lotka_Volterra_sob_ru%C3%ADdo_branco. Acesso em ago. 2024.
3. SCHERER, C. Métodos computacionais da física. 2. ed ed. São Paulo: Liv. da Física, 2010.
4. KHASMINSKII, R. Z.; KLEBANER, F. C. Long term behavior of solutions of the Lotka-Volterra system under small random perturbations. The Annals of Applied Probability, v. 11, n. 3, 1 ago. 2001.