Julia: mudanças entre as edições
| (27 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 26: | Linha 26: | ||
== Testes de Velocidade == | == Testes de Velocidade == | ||
A fim de pessoalmente testar a velocidade da linguagem de programação, foi escrito um programa em Julia de maneira similar ao programa de Python para o FTCS aplicado na Equação de Difusão (também conhecida como Equação do Calor). | |||
A Equação da Difusão em uma dimensão pode ser escrita da forma: | |||
<center><math>\frac{df}{dt}=\frac{d^{2}f}{dx^{2}}</math></center> | |||
No método de FTCS (Forward-Time Central-Space) definimos a derivada em t na forma não simetrizada (forward) e as derivadas em x na forma simetrizada: | |||
<center><math>\frac{df}{dt} = \frac{f(x, t+dt) - f(x,t)}{dt}</math></center> | |||
<p> | |||
<center><math>\frac{d^{2}f}{dx^{2}} = \frac{f(x+dx, t) + f(x-dx, t) - 2f(x,t)}{dx^{2}}</math></center> | |||
E substuindo na equação da difusão, em notação discreta temos: | |||
<center><math>f_{j}^{n+1} = f_{j}^{n} + D\frac{dt}{(dx)^{2}}[f_{j+1}^{n} + f_{j-1}^{n} - 2 f_{j}^{n}]</math></center> | |||
'''Observação:''' esse procedimento funciona bem se <math>k=D\frac{dt}{(dx)^{2}} <= 1/2</math>, segundo análise de estabilidade do método. | |||
Dessa forma, foi escrito um programa para integrar a Equação de Difusão através do método de FTCS nas linguagens Python e Julia. | |||
Para '''Python''': | |||
<pre> | |||
# FTCS aplicado na equacao da difusao. Linguagem: PYTHON | |||
import copy | |||
import numpy as np | |||
import matplotlib.pyplot as plt | |||
def init(): | |||
L=50;D=1.;dt=0.05;dx=1.;t=0;tmax=100. | |||
k=D*dt/(dx*dx) | |||
return L,k,dt,t,tmax | |||
L,k,dt,t,tmax = init() | |||
x = np.arange(0,L,1) | |||
f = np.zeros(x.shape) | |||
a = int(L/3) | |||
b = int(2*L/3) | |||
f[a:b]=1. | |||
f1 = copy.deepcopy(f) | |||
f2 = copy.deepcopy(f) | |||
while t<tmax: | |||
t+=dt | |||
f1[1:L-1]=f[1:L-1]+k*(f[0:L-2]+f[2:L]-2*f[1:L-1]) | |||
f1[L-1]=f[L-1]+k*(f[L-2]+f[0]-2*f[L-1]) | |||
f1[0]=f[0]+k*(f[1]+f[L-1]-2*f[0]) | |||
f=copy.deepcopy(f1) | |||
sum0=sum(f1) | |||
sum1=sum(f2) | |||
print("Integral em t=0: %7.4f" % sum0) | |||
print("Integral em tmax: %7.4f" % sum1) | |||
plt.plot(x,f,x,f2) | |||
plt.show() | |||
</pre> | |||
Em '''Julia''': | |||
<pre> | |||
# FTCS aplicado na equacao da difusao. Linguagem: JULIA | |||
using PyPlot | |||
L=50 | |||
D=1. | |||
dt=0.05 | |||
dx=1. | |||
t=0 | |||
tmax=100. | |||
k=D*dt/(dx*dx) | |||
x = collect(0:1:L-1) | |||
f = zeros(L) | |||
f1 = zeros(L) | |||
a = trunc(Int, L/3) | |||
b = trunc(Int, 2*L/3) | |||
f[a+1:b] .= 1. | |||
f2 = deepcopy(f) | |||
while t<tmax | |||
global t+=dt | |||
f1[2:L-1] = f[2:L-1] + k*(f[1:L-2] + f[3:L] - 2*f[2:L-1]) | |||
f1[L] = f[L] + k*(f[L-1] + f[1] - 2*f[L]) | |||
f1[1] = f[1] + k*(f[2] + f[L] - 2*f[1]) | |||
global f = deepcopy(f1) | |||
end | |||
sum0 = sum(f1) | |||
sum1 = sum(f2) | |||
println("Integral em t=0: ", sum0) | |||
println("Integral em tmax: ", sum1) | |||
plt.plot(x,f,x,f2) | |||
plt.show() | |||
</pre> | |||
Foi testado o tempo de execução da parte principal dos dois programas (isto é, sem fazer o gráfico dos resultados), através do timer do terminal, como mostra na próxima figura: | |||
<center>[[Arquivo:Ftcs_time.png|border]] | |||
'''Legenda:''' Tempo de execução dos dois programas, em Julia e em Python, para o método de FTCS aplicado à Equação de Difusão | |||
</center> | |||
É possível perceber, através da figura acima, que o tempo de execução de Python para o FTCS aplicado à Equação de Difusão é menor do que o de Julia. Em razão disso, foi testado um programa simples, como mostra abaixo, que incrementa uma variável 10 vezes, sendo o seu valor inicial 0. | |||
<center>[[Arquivo:For.png|border]] | |||
'''Legenda:''' Programa para incrementar o valor de uma variável, nesse caso ''i'', 10 vezes, escrito em Julia e em Python | |||
</center> | |||
E posteriormente, novamente, foi testado o tempo de execução da parte principal dos programas através do terminal: | |||
<center>[[Arquivo:For_time.png|border]] | |||
'''Legenda:''' Tempo de execução dos dois programas, em Julia e em Python, para o programa que incrementa o valor da variável 10 vezes | |||
</center> | |||
É possível perceber que para esse simples programa de incrementação, Python ainda obtém melhor performance do que Julia. | |||
== Performance de Julia == | |||
Tentando entender o que traria tal performance em Cálculo Numérico para Julia, foi chegado à conclusão de que ser uma linguagem que se utilizada de ''variáveis dinâmicas'' e ''multi-métodos'' seria uma das grandes contribuições da linguagem. | |||
'''Variáveis dinâmicas:''' | |||
Em Python as variáveis são interpretadas em runtime, ou seja, '''tempo de execução''' => o programa checa toda hora se a variável mudou e isso torna ele mais lento | |||
'''Variáveis estáticas:''' | |||
Em C as variáveis são fixas, e isso é visto é em '''tempo de compilação''' => precisa pensar nas variáveis e isso torna o tempo de programação mais lento | |||
Em Julia isso é basicamente opcional, não é preciso definir as variáveis, mas é possível, e elas podem mudar dinamicamente, em tempo de execução. E ainda, Julia se utiliza de multi-métodos para não ter que lidar com a constante checagem dos tipos das variáveis, como Python faz! | |||
'''Despacho único:''' | |||
Em geral, em linguagens de programação funções podem ter o mesmo nome, portanto deve existir algum mecanismo que irá realizar o despacho da | |||
chamada de tais funções, resolvendo o conflito dos nomes iguais. | |||
Na maioria das linguagens de programação populares (python, C++, javascript, C#), o despacho da chamada de funções ocorre apenas levando em consideração o primeiro argumento da mesma, tal mecanismo é chamado de '''despacho único'''. Como exemplo, vamos considerar o seguinte exemplo em python | |||
<syntaxhighlight lang="python"> | |||
class MyClass1: | |||
def some_function(self, a): | |||
print("Value-1:", a) | |||
class MyClass2: | |||
def some_function(self, a): | |||
print("Value-2:", a) | |||
my_obj_1 = MyClass1() | |||
my_obj_2 = MyClass2() | |||
</syntaxhighlight> | |||
Existem duas funções com o nome <code>some_function</code>, e obviamente tentar chamá-las dessa forma <code>some_function("some_text")</code> não funciona. A chamada correta é feita da seguinte forma: | |||
* <code>my_obj_1.some_function("some_text")</code>: Executa a função em <code>MyClass1</code>. | |||
* <code>my_obj_2.some_function("some_text")</code>: Executa a função em <code>MyClass2</code> | |||
A sintaxe para chamar funções <code>my_obj.some_function(...)</code> é apenas o padrão adotado pelo python, mas ela é equivalente a <code>some_function(my_obj, ...) </code>, ou seja, quem determina qual função é de fato executada, é o primeiro argumento da chamada, os demais argumentos não são levados em consideração no momento do despacho. | |||
'''Despacho múltiplo:''' | |||
Em Julia, o despacho da execução de funções leva em consideração todos os seus argumentos, não apenas o primeiro, esse mecanismo leva o nome de '''despacho múltiplo'''. Para ilustrar o despacho múltiplo em ação, considere que estamos trabalhando em um código de dinâmica de partículas, e estamos precisando escrever uma função para calcular a energia potencial do sistema, que depende das massas, então podemos implementar a seguinte função | |||
<syntaxhighlight lang="julia"> | |||
function potencial_energy(mass, positions, pars) | |||
println("Calculando energia potencial") | |||
end | |||
</syntaxhighlight> | |||
em que | |||
* mass: Massas das partícula. | |||
* positions: Posições das partículas. | |||
* pars: Parâmetros do potencial em questão. | |||
mas suponha que agora estamos interessados em explorar o sistemas quando todas as massas são iguais, e desejamos usar essa condição para melhorar o desempenho do cálculo da energia potencial. Poderíamos adicionar algumas estruturas condicionais dentro da função acima para isso, mas uma melhor forma é fazer com que a função <code>potencial_energy</code> despache no argumento <code>mass</code>, então, precisamos criar um tipo que represente massas iguais, que apenas vai possui um único atributo (a massa comum a todas as partículas) e um novo método para <code>potencial_energy</code> que despacha utilizando esse tipo: | |||
<syntaxhighlight lang="julia"> | |||
struct SameMass | |||
masss::Float64 | |||
end | |||
function potencial_energy(mass::SameMass, positions, pars) | |||
println("Calculando energia potencial com otimização para massas iguais") | |||
end | |||
</syntaxhighlight> | |||
Esse novo método possui uma implementação otimizada para o caso em que todas as massas são iguais. Nada precisa mudar no código que chama <code>potencial_energy</code>, pois o despacho múltiplo vai fazer com que seja executado a implementação correta. | |||
Agora suponha que estamos interessado em outro potencial (Potencial2), ao invés de criar uma nova função para Potencial2, vamos fazer com que <code>potencial_energy</code> despache no argumento <code>pars</code> | |||
<syntaxhighlight lang="julia"> | |||
struct Potencial2 | |||
par1::Int | |||
par2::Float64 | |||
end | |||
function potencial_energy(mass, positions, pars::Potencial2) | |||
println("Calculando energia potencial para Potencial2") | |||
end | |||
</syntaxhighlight> | |||
Ainda, podemos fazer um método para Potencial2 que é otimizado para todas as massas iguais | |||
<syntaxhighlight lang="julia"> | |||
function potencial_energy(mass::SameMass, positions, pars::Potencial2) | |||
println(""Calculando energia potencial com otimização para massas iguais para Potencial2") | |||
end | |||
</syntaxhighlight> | |||
Agora que estamos trabalhando com dois potencias, é inteligente também criar um tipo para o primeiro potencial, que vamos chamar de Potencial1: | |||
<syntaxhighlight lang="julia"> | |||
struct Potencial1 | |||
par1::Float64 | |||
par2::Float64 | |||
end | |||
</syntaxhighlight> | |||
O seguinte exemplo utiliza os métodos que criamos | |||
<syntaxhighlight lang="julia"> | |||
positions = [] # Suponha que as posições das partículas estejam aqui | |||
pars_1 = Potencial1(3.14, 2.71) | |||
pars_2 = Potencial2(137, 3.48) | |||
mass = [] # Suponha que as diferentes massas das partículas estejam aqui | |||
same_mass = SameMass(1) | |||
potencial_energy(mass, positions, pars_1) | |||
potencial_energy(mass, positions, pars_2) | |||
potencial_energy(same_mass, positions, pars_1) | |||
potencial_energy(same_mass, positions, pars_2) | |||
</syntaxhighlight> | |||
executando, temos a seguinte saída: | |||
Calculando energia potencial | |||
Calculando energia potencial para Potencial2 | |||
Calculando energia potencial com otimização para massas iguais | |||
Calculando energia potencial com otimização para massas iguais para Potencial2 | |||
== Performance de Julia: na prática == | |||
Para resumir, temos: | |||
Python => dynamic (variáveis dinâmicas) single dispatch (métodos únicos) | |||
C++ => static (variáveis estáticas) single dispatch | |||
Julia => dynamic multiple dispatch | |||
Na prática, é mostrado abaixo um exemplo da performance de Julia como linguagem de programação em dynamic multiple dispatch. | |||
O mesmo programa foi escrito em Julia e em C++. | |||
Em '''Julia''': | |||
<pre> | |||
abstract type Animal end | |||
struct Cachorro <: Animal | |||
nome::String | |||
end | |||
struct Gato <: Animal | |||
nome::String | |||
end | |||
# Função de encontro que recebe tipo genérico de animal | |||
function encontroDeAnimais(a::Animal, b::Animal) | |||
acao = encontro(a,b) | |||
println("$(a.nome) encontra $(b.nome) e $acao") | |||
end | |||
# Funções de expressão única que recebem diferentes tipos de animais | |||
encontro(a::Cachorro, b::Cachorro) = "cheira" | |||
encontro(a::Cachorro, b::Gato) = "persegue" | |||
encontro(a::Gato, b::Gato) = "lambe" | |||
encontro(a::Gato, b::Cachorro) = "ignora" | |||
# Instanciando os bichinhos | |||
gato1 = Gato("Luciene Maria") | |||
gato2 = Gato("Mel") | |||
cachorro1 = Cachorro("Batata") | |||
cachorro2 = Cachorro("Snoopy") | |||
# Chamando função encontroDeAnimais | |||
encontroDeAnimais(gato1, gato2) | |||
encontroDeAnimais(gato1, cachorro2) | |||
encontroDeAnimais(cachorro1, cachorro2) | |||
</pre> | |||
Em '''C++''': | |||
<pre> | |||
#include <iostream> | |||
using namespace std; | |||
class Animal { | |||
public: | |||
string nome; | |||
}; | |||
string encontro(Animal a, Animal b) {} | |||
// Função de encontro que recebe tipo genérico de animal | |||
void encontroDeAnimais(Animal a, Animal b) { | |||
string acao = encontro(a,b); | |||
cout << a.nome << " encontra " << b.nome << " e " << acao << endl; | |||
} | |||
class Cachorro:public Animal {}; | |||
class Gato:public Animal {}; | |||
// Funções de expressão única que recebem diferentes tipos de animais | |||
string encontro(Cachorro a, Cachorro b) { return "cheira"; } | |||
string encontro(Cachorro a, Gato b) { return "persegue"; } | |||
string encontro(Gato a, Gato b) { return "lambe"; } | |||
string encontro(Gato a, Cachorro b) { return "ignora"; } | |||
int main() { | |||
// Instanciando os bichinhos | |||
Gato gato1; gato1.nome = "Luciene Maria"; | |||
Gato gato2; gato2.nome = "Mel"; | |||
Cachorro cachorro1; cachorro1.nome = "Batata"; | |||
Cachorro cachorro2; cachorro2.nome = "Snoopy"; | |||
// Chamando função encontroDeAnimais | |||
encontroDeAnimais(gato1, gato2); | |||
encontroDeAnimais(gato1, cachorro2); | |||
encontroDeAnimais(cachorro1, cachorro2); | |||
return 0; | |||
} | |||
</pre> | |||
Para '''Julia''' nós obtemos o seguinte '''resultado''': | |||
<pre> | |||
Luciene Maria encontra Mel e lambe | |||
Luciene Maria encontra Snoopy e ignora | |||
Batata encontra Snoopy e cheira | |||
</pre> | |||
Para '''C++''' o '''resultado''' é: | |||
<pre> | |||
Luciene Maria encontra Mel e | |||
Falha de Segmentação | |||
</pre> | |||
Isso acontece porque C++ não aceita que uma função utilize-se de uma variável sem antes saber qual o tipo dessa variável! Por isso, poder utilizar-se de variáveis dinâmicas quando há multi-métodos é um diferencial que acaba por incrementar a performance de Julia como linguagem de programação visada para o Cálculo Numérico. | |||
'''Observação:''' é importante ressaltar que os testes feitos não são conclusivos para debater a performance de Julia, em termos estatísticos, e além disso, ser uma linguagem de programação que utiliza de variáveis dinâmicas e multi-métodos não é o único motivo pelo qual Julia poderia trazer tal performance em Cálculo Numérico. Podemos ainda contar com a sua capacidade de '''metaprogramação''', ou seja, Julia pode usar macros e eles são aplicados em tempo de interpretação. Há ainda outros fatores da construção da linguagem que contribuem para sua performance que aqui não foram citados. | |||
== Aprendendo Julia == | |||
'''Ambiente de programação''' | |||
Após feita a instalação de Julia, para abri-la no seu terminal de comando é preciso apenas digitar: <pre>$julia</pre> para entrar em seu ambiente de programação. | |||
É possível, também, programar em um arquivo de texto (salvo como .jl) e executar o programa pelo terminal, fazendo simplesmente: | |||
<pre> | |||
$julia programa.jl | |||
</pre> | |||
'''Impressão na tela''' | |||
<pre> | |||
println("Hello World") | |||
Saída: | |||
Hello World | |||
</pre> | |||
'''Variáveis''' | |||
Variáveis são atribuídas dinamicamente e podem mudar. | |||
<pre> | |||
s = 1 | |||
s = "Oi" | |||
println(s) | |||
println(typeof(s)) | |||
Saída: | |||
Oi | |||
String | |||
</pre> | |||
<pre> | |||
s::String | |||
s = 1 | |||
println(s) | |||
Saída: | |||
TypeError: in typeassert, expected String, got Int32 | |||
</pre> | |||
'''Condicionais''' | |||
<pre> | |||
cats = 12 | |||
if cats < 1 | |||
println("You should adopt a cat.") | |||
elseif cats >= 1 && cats <=6 | |||
println("Not enough cats.") | |||
elseif cats >= 7 && cats <= 12 | |||
println("Still not enough cats.") | |||
else | |||
println("Gato have more cats.") | |||
end | |||
Saída: | |||
Still not enough cats. | |||
</pre> | |||
<pre> | |||
i = 0 | |||
while (i < 10) | |||
global i += 1 | |||
println(i) | |||
end | |||
Saída: | |||
1 | |||
2 | |||
3 | |||
4 | |||
5 | |||
6 | |||
7 | |||
8 | |||
9 | |||
10 | |||
</pre> | |||
<pre> | |||
for i = 1:10 | |||
println(i) | |||
end | |||
Saída: | |||
1 | |||
2 | |||
3 | |||
4 | |||
5 | |||
6 | |||
7 | |||
8 | |||
9 | |||
10 | |||
</pre> | |||
<pre> | |||
for i in [1,2,3] | |||
println(i) | |||
end | |||
Saída: | |||
1 | |||
2 | |||
3 | |||
</pre> | |||
'''Arrays''' | |||
<pre> | |||
# Criando um array de zeros | |||
a1 = zeros() | |||
println(a1) | |||
# Posso definir o tipo e o tamanho do Array (linhas, colunas) também | |||
a1 = zeros(Int32, 1, 4) | |||
println(a1) | |||
Saída: | |||
0.0 | |||
[0 0 0 0] | |||
</pre> | |||
<pre> | |||
# Criando um array do tipo inteiro | |||
a2 = Array{Int32} | |||
println(a2) | |||
# Criando um array (de outra maneira) do tipo float | |||
a3 = Float64[] | |||
println(a3) | |||
Saída: | |||
Array{Int32,N} where N [...] | |||
Float64[] | |||
</pre> | |||
<pre> | |||
# Criando um array e definindo valores | |||
a4 = [1,2,3] | |||
#Imprimindo a4 | |||
println("Array: ", a4) | |||
Saída: | |||
Array: [1, 2, 3] | |||
</pre> | |||
<pre> | |||
a4 = [1,2,3] | |||
# Imprimindo valor de um indíce específico | |||
println("Imprimindo primeiro elemento: ", a4[1]) | |||
# Imprimindo último valor do array | |||
println("Imprimindo último elemento: ",a4[end]) | |||
Saída: | |||
Imprimindo primeiro elemento: 1 | |||
Imprimindo último elemento: 3 | |||
</pre> | |||
<pre> | |||
a4 = [1,2,3] | |||
println(a4[2]) | |||
# Valores podem mudar (diferente de Tuplas, que veremos adiante) | |||
a4[2] = 4 | |||
println(a4[2]) | |||
Saída: | |||
2 | |||
4 | |||
</pre> | |||
<pre> | |||
a4 = [1,2,3] | |||
println(a4) | |||
# Número de elementos | |||
println("Imprimindo número de elementos: ",length(a4)) | |||
Saída: | |||
[1, 2, 3] | |||
Imprimindo número de elementos: 3 | |||
</pre> | |||
<pre> | |||
a4 = [1,2,3] | |||
# Soma os valores do array | |||
println("Imprimindo soma dos elementos: ",sum(a4)) | |||
# Põe os valores começando no índice 2 | |||
splice!(a4, 2:1, [8,9]) | |||
println("Imprimindo Array tendo feito splice!(a4, 2:1, [8,9]): ",a4) | |||
# Remove os itens do índice 2 ao 3 | |||
4splice!(a4, 2:3) | |||
println("Imprimindo Array tendo feito splice!(a4, 2:3): ",a4) | |||
Saída: | |||
Imprimindo soma dos elementos: 6 | |||
Imprimindo Array tendo feito splice!(a4, 2:1, [8,9]): [1, 8, 9, 2, 3] | |||
Imprimindo Array tendo feito splice!(a4, 2:3): [1, 2, 3] | |||
</pre> | |||
<pre> | |||
a4 = [1,2,3] | |||
# Pegar valor máximo e valor mínimo | |||
println("Imprimindo valor máximo: ",maximum(a4)) | |||
println("Imprimindo Array valor mínimo: ",minimum(a4)) | |||
# Multiplicando todos os elementos do array por outro número sem precisar de um for | |||
println("Imprimindo multiplicação dos elementos por 2: ",a4 * 2) | |||
Saída: | |||
Imprimindo valor máximo: 3 | |||
Imprimindo Array valor mínimo: 1 | |||
Imprimindo multiplicação dos elementos por 2: [2, 4, 6] | |||
</pre> | |||
<pre> | |||
# Arrays podem conter funções | |||
a5 = [sin, cos, tan] | |||
for n in a5 | |||
println(n(0)) | |||
end | |||
Saída: | |||
0.0 | |||
1.0 | |||
0.0 | |||
</pre> | |||
<pre> | |||
# Para os acostumados com range | |||
a6 = collect(1:5) | |||
println(a6) | |||
Saída: | |||
[1, 2, 3, 4, 5] | |||
</pre> | |||
'''Tuplas''' | |||
A maioria das funções de array funciona com tuplas. | |||
<pre> | |||
# Valores não podem mudar | |||
t1 = (1,2,3,4) | |||
println(t1[2]) | |||
t1[2] = 5 | |||
println(t1[2]) | |||
Saída: | |||
2 | |||
MethodError: no method matching setindex!(::NTuple{4,Int32}, ::Int32, ::Int32) | |||
</pre> | |||
<pre> | |||
# Imprimindo a tupla inteira | |||
println(t1) | |||
# Imprimindo a tupla inteira | |||
for i in t1 | |||
println(i) | |||
end | |||
Saída: | |||
(1, 2, 3, 4) | |||
1 | |||
2 | |||
3 | |||
4 | |||
</pre> | |||
'''Dicionários''' | |||
A palavra-chave deve ser única. | |||
<pre> | |||
d1 = Dict("pi"=>3.14, "e"=>2.718) | |||
# Imprimir um valor | |||
println(d1["pi"]) | |||
Saída: | |||
3.14 | |||
</pre> | |||
<pre> | |||
d1 = Dict("pi"=>3.14, "e"=>2.718) | |||
# Imprimindo todas as palavras-chaves | |||
println(keys(d1)) | |||
# Imprimindo todos os valores | |||
println(values(d1)) | |||
# Adicionar uma palavra-chave | |||
d1["golden"] = 1.618 | |||
# Deleter uma palavra-chave | |||
delete!(d1, "pi") | |||
# Imprimindo todas as palavras-chaves | |||
println(keys(d1)) | |||
# Imprimindo todos os valores | |||
println(values(d1)) | |||
Saída: | |||
["pi", "e"] | |||
[3.14, 2.718] | |||
["e", "golden"] | |||
[2.718, 1.618] | |||
</pre> | |||
<pre> | |||
d1 = Dict("pi"=>3.14, "e"=>2.718) | |||
# Ver se a palavra-chave existe | |||
println(haskey(d1, "pi")) | |||
# Imprimindo palavras-chaves E valores | |||
for kv in d1 | |||
println(kv) | |||
end | |||
Saída: | |||
true | |||
"pi" => 3.14 | |||
"e" => 2.718 | |||
</pre> | |||
'''Sets''' | |||
Sets são arrays com elementos únicos. | |||
<pre> | |||
st1 = Set(["Jim", "Pam", "Jim"]) | |||
# Ele não pega os elementos repetidos | |||
println(st1) | |||
Saída: | |||
Set(["Pam", "Jim"]) | |||
</pre> | |||
<pre> | |||
st1 = Set(["Jim", "Pam", "Jim"]) | |||
# Adicionando um elemento | |||
push!(st1, "Michael") | |||
println(st1) | |||
# Ver se um elemento está no Set | |||
println(in("Dwight", st1)) | |||
Saída: | |||
Set(["Pam", "Michael", "Jim"]) | |||
false | |||
</pre> | |||
<pre> | |||
st1 = Set(["Jim", "Pam", "Jim"]) | |||
st2 = Set(["Stanley", "Meredith"]) | |||
# Combinando Sets | |||
println(union(st1, st2)) | |||
# Imprimindo todo o elemento que os dois Sets tem em comum | |||
println(intersect(st1, st2)) | |||
# Imprimindo elementos que estão no primeiro Set, mas não no segundo | |||
println(setdiff(st1, st2)) | |||
Saída: | |||
Set(["Jim", "Meredith", "Stanley", "Pam"]) | |||
Set(String[]) | |||
Set(["Pam", "Jim"]) | |||
</pre> | |||
'''Funções''' | |||
<pre> | |||
using Printf | |||
# Função de expressão única | |||
soma(x,y) = x + y | |||
x, y = 1, 2 | |||
@printf("%d + %d = %d\n", x, y, x+y) | |||
Saída: | |||
1 + 2 = 3 | |||
</pre> | |||
<pre> | |||
# Função de múltiplas expressões | |||
function adoptACat(cats) | |||
if cats <= 1 | |||
println("You should adopt a cat.") | |||
else | |||
println("You should adopt a cat. They're cute.") | |||
end | |||
end | |||
adoptACat(2) | |||
Saída: | |||
You should adopt a cat. They're cute. | |||
</pre> | |||
<pre> | |||
v1 = 5 | |||
function changeV1(v1) | |||
v1 = 10 | |||
end | |||
changeV1(v1) | |||
println(v1) | |||
Saída: | |||
5 | |||
</pre> | |||
<pre> | |||
v1 = 5 | |||
function changeV1(v1) | |||
v1 = 10 | |||
return v1 | |||
end | |||
changeV1(v1) | |||
println(v1) | |||
v2 = changeV1(v1) | |||
println(v2) | |||
Saída: | |||
5 | |||
10 | |||
</pre> | |||
<pre> | |||
# Usando variáveis globais dentro da função | |||
v1 = 5 | |||
function changeV12() | |||
global v1 = 10 | |||
end | |||
changeV12() | |||
println(v1) | |||
Saída: | |||
10 | |||
</pre> | |||
<pre> | |||
# Quando não sei quantos argumentos vou passar | |||
function soma(args...) | |||
sum = 0 | |||
for i in args | |||
sum += i | |||
end | |||
println(sum) | |||
end | |||
soma(1,2,3) | |||
Saída: | |||
6 | |||
</pre> | |||
<pre> | |||
# Retornando mais de um valor | |||
function retorna2(valor) | |||
return (valor + 1, valor + 2) | |||
end | |||
println(retorna2(4)) | |||
Saída: | |||
(5, 6) | |||
</pre> | |||
<pre> | |||
# Map é uma função anônima que aplica uma função para cada elemento | |||
v = map(x -> x * x, [1,2,3]) | |||
println(v) | |||
Saída: | |||
[1, 4, 9] | |||
</pre> | |||
'''Structs''' | |||
<pre> | |||
struct Estudante | |||
name::String | |||
saldoTRI::Float32 | |||
cartaoUFRGS::Int | |||
end | |||
# Criando um objeto | |||
estudante1 = Estudante("Raquel", 10.50, 244449) | |||
println(estudante1.name, "\n", estudante1.saldoTRI, "\n", estudante1.cartaoUFRGS) | |||
Saída: | |||
Raquel | |||
10.5 | |||
244449 | |||
</pre> | |||
'''Tipos Abstratos''' | |||
Tipos abstratos não podem ser instanciados como as Structs (instanciar => fazer estudante1 = | |||
Estudante(“Raquel”, 10.50, 244449) => criar um objeto) MAS podem ter subTipos e isso é muito | |||
útil! | |||
<pre> | |||
abstract type animal end | |||
struct cachorro <: animal | |||
nome::String | |||
latido::String | |||
end | |||
struct gato <: animal | |||
nome::String | |||
miado::String | |||
end | |||
cachorro1 = cachorro("Urso", "Au Au") | |||
gato1 = gato("Lucia Irene", "Miau") | |||
# Criando funções pros subTipos | |||
function fazerSom(animal::cachorro) | |||
println("$(animal.nome) diz $(animal.latido)") | |||
end | |||
function fazerSom(animal::gato) | |||
println("$(animal.nome) diz $(animal.miado)") | |||
end | |||
fazerSom(cachorro1) | |||
fazerSom(gato1) | |||
Saída: | |||
Urso diz Au Au | |||
Lucia Irene diz Miau | |||
</pre> | |||
== Modularizando códigos em Julia == | |||
== Módulos == | |||
Na Julia é possível agrupar pedaços de códigos em módulos, cuja função é puramente de organização. Módulos são definidos pela palavra-chave `module` e eles introduzem um novo escopo, por exemplo: | |||
<syntaxhighlight lang="julia"> | |||
module MyModule | |||
struct SomeStruct | |||
some_attr::Float64 | |||
end | |||
function sum(a ,b) | |||
println(a + b) | |||
end | |||
function product(a ,b) | |||
println(a * b) | |||
end | |||
end | |||
</syntaxhighlight> | |||
Para acessar o conteúdo dos módulos fora deles, é necessário qualificar o nome do item de interesse, por exemplo, podemos utilizar a função `sum` da seguinte forma: | |||
<syntaxhighlight lang="julia"> | |||
module MyModule | |||
... | |||
end | |||
function main() | |||
MyModule.sum(1, 3) | |||
end | |||
main() | |||
</syntaxhighlight> | |||
Em python, cada arquivo <code>.py</code> é um módulo, em Julia não existe esse conceito, um arquivo <code>.jl</code> pode conter diversos módulos e um módulo pode estar espalhado em diversos arquivos. | |||
* Mais informações sobre módulos podem ser encontradas no [https://docs.julialang.org/en/v1/manual/modules/#modules manual da Julia] | |||
== Separando o código em arquivos == | |||
A Julia não possui o conceito de código em diferentes arquivos, assim como é no python por exemplo (cada arquivo é um módulo), mas podemos, apenas por questão de conveniência, separar o código em diferentes arquivos, no entanto um deles vai ser o arquivo principal, e seu dever e incluir todos os outros arquivos utilizando o comando `include`. | |||
== Criando pacotes == | |||
Vamos criar um pacote que pode ser utilizado em qualquer lugar em sua máquina (utilizando <code>using MyPkgName</code>), para isso navegue para o local em que se deseja color os arquivos do pacote, abra um REPL e execute | |||
<syntaxhighlight lang="julia"> | |||
using PkgTemplate | |||
t = Template(dir=".") | |||
t("MyPkg") | |||
</syntaxhighlight> | |||
Isto irá automaticamente criar uma pasta contendo os arquivos do pacote na localização atual. Para podermos utilizá-lo em qualquer lugar, precisamos adicioná-lo no ambiente atual, que pode ser feito da seguinte forma: | |||
* Utilizando o mesmo REPL que foi utilizado para criar o pacote, entre no modo de gerenciamento de pacotes (aparte ] com a entrada do REPL vazia) | |||
* Execute o comanndo | |||
:<syntaxhighlight lang="julia"> | |||
pkg> activate MyPkg | |||
</syntaxhighlight> | |||
a partir de agora, qualquer arquivo pode utilizar | |||
<syntaxhighlight lang="julia"> | |||
using MyPkg | |||
</syntaxhighlight> | |||
* Para mais informações sobre como gerenciar/criar pacotes em julia, [https://pkgdocs.julialang.org/v1/#**1.**-Introduction clique aqui]. | |||
* Para mais informações sobre como criar pacotes com o PkgTemplate, [https://juliaci.github.io/PkgTemplates.jl/stable/user/#PkgTemplates-User-Guide clique aqui]. | |||
Edição atual tal como às 11h31min de 24 de agosto de 2024
Julia é uma linguagem relativamente nova de programação que começou a ser desenvolvida em 2009 por Jeff Bezanson, Stefan Karpinski, Viral B. Shah, e Alan Edelman, um grupo do MIT. Ela foi oficialmente lançada para o mundo em 2012.
Em uma entrevista, quando perguntaram a Alan o por quê do nome Julia, ele disse que numa conversa anos atrás alguém sugeriu que Julia seria um bom nome para uma linguagem de programação.
Julia pode ser usada para propósitos gerais de programação, assim como Python, mas em sua criação foi visada a utilização de Julia para Cálculo Numérico.
Aspectos Gerais
Julia é uma linguagem de alto nível, isso significa, de maneira sucinta, que ela não é executada utilizando somente o processador, assim como acontece com linguagens de baixo nível, como Assembly, por exemplo.
É escrita em C, C++, e Scheme, usando a estrutura do compilador LLVM (para melhor entendimento, o compilador de C é o GCC, por exemplo), enquanto a maior parte da biblioteca padrão de Julia é implementada na própria Julia.
Um fato importante sobre Julia para os programadores de Python é que todas as bibliotecas de Python são usáveis através de um comando simples: PyCall.
Um fato importante sobre Julia para os programadores de C é que Julia possui APIs (Interfaces de Programação de Aplicativos) especiais para chamada de funções em C diretamente.
Velocidade
De acordo com testes feitos pelos próprios criadores de Julia, sua velocidade é similar com a de C.
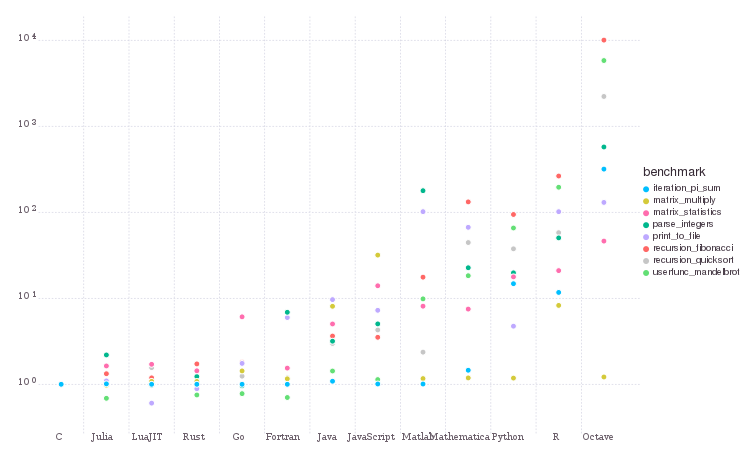
Fonte: [1]
Testes de Velocidade
A fim de pessoalmente testar a velocidade da linguagem de programação, foi escrito um programa em Julia de maneira similar ao programa de Python para o FTCS aplicado na Equação de Difusão (também conhecida como Equação do Calor).
A Equação da Difusão em uma dimensão pode ser escrita da forma:
No método de FTCS (Forward-Time Central-Space) definimos a derivada em t na forma não simetrizada (forward) e as derivadas em x na forma simetrizada:
E substuindo na equação da difusão, em notação discreta temos:
Observação: esse procedimento funciona bem se , segundo análise de estabilidade do método.
Dessa forma, foi escrito um programa para integrar a Equação de Difusão através do método de FTCS nas linguagens Python e Julia.
Para Python:
# FTCS aplicado na equacao da difusao. Linguagem: PYTHON
import copy
import numpy as np
import matplotlib.pyplot as plt
def init():
L=50;D=1.;dt=0.05;dx=1.;t=0;tmax=100.
k=D*dt/(dx*dx)
return L,k,dt,t,tmax
L,k,dt,t,tmax = init()
x = np.arange(0,L,1)
f = np.zeros(x.shape)
a = int(L/3)
b = int(2*L/3)
f[a:b]=1.
f1 = copy.deepcopy(f)
f2 = copy.deepcopy(f)
while t<tmax:
t+=dt
f1[1:L-1]=f[1:L-1]+k*(f[0:L-2]+f[2:L]-2*f[1:L-1])
f1[L-1]=f[L-1]+k*(f[L-2]+f[0]-2*f[L-1])
f1[0]=f[0]+k*(f[1]+f[L-1]-2*f[0])
f=copy.deepcopy(f1)
sum0=sum(f1)
sum1=sum(f2)
print("Integral em t=0: %7.4f" % sum0)
print("Integral em tmax: %7.4f" % sum1)
plt.plot(x,f,x,f2)
plt.show()
Em Julia:
# FTCS aplicado na equacao da difusao. Linguagem: JULIA
using PyPlot
L=50
D=1.
dt=0.05
dx=1.
t=0
tmax=100.
k=D*dt/(dx*dx)
x = collect(0:1:L-1)
f = zeros(L)
f1 = zeros(L)
a = trunc(Int, L/3)
b = trunc(Int, 2*L/3)
f[a+1:b] .= 1.
f2 = deepcopy(f)
while t<tmax
global t+=dt
f1[2:L-1] = f[2:L-1] + k*(f[1:L-2] + f[3:L] - 2*f[2:L-1])
f1[L] = f[L] + k*(f[L-1] + f[1] - 2*f[L])
f1[1] = f[1] + k*(f[2] + f[L] - 2*f[1])
global f = deepcopy(f1)
end
sum0 = sum(f1)
sum1 = sum(f2)
println("Integral em t=0: ", sum0)
println("Integral em tmax: ", sum1)
plt.plot(x,f,x,f2)
plt.show()
Foi testado o tempo de execução da parte principal dos dois programas (isto é, sem fazer o gráfico dos resultados), através do timer do terminal, como mostra na próxima figura:
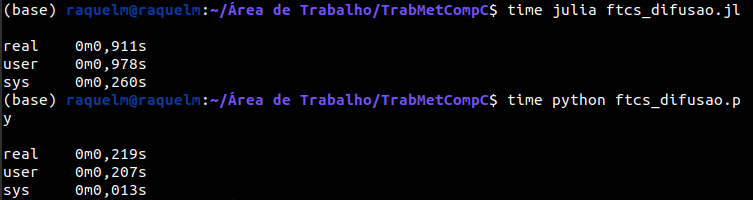
Legenda: Tempo de execução dos dois programas, em Julia e em Python, para o método de FTCS aplicado à Equação de Difusão
É possível perceber, através da figura acima, que o tempo de execução de Python para o FTCS aplicado à Equação de Difusão é menor do que o de Julia. Em razão disso, foi testado um programa simples, como mostra abaixo, que incrementa uma variável 10 vezes, sendo o seu valor inicial 0.
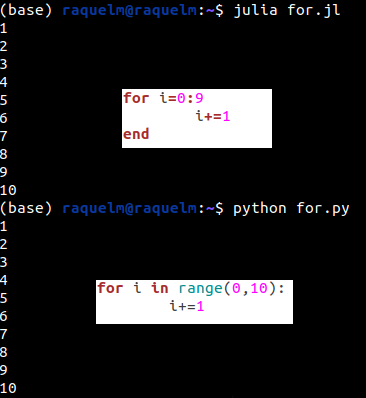
Legenda: Programa para incrementar o valor de uma variável, nesse caso i, 10 vezes, escrito em Julia e em Python
E posteriormente, novamente, foi testado o tempo de execução da parte principal dos programas através do terminal:
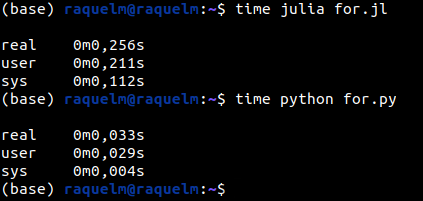
Legenda: Tempo de execução dos dois programas, em Julia e em Python, para o programa que incrementa o valor da variável 10 vezes
É possível perceber que para esse simples programa de incrementação, Python ainda obtém melhor performance do que Julia.
Performance de Julia
Tentando entender o que traria tal performance em Cálculo Numérico para Julia, foi chegado à conclusão de que ser uma linguagem que se utilizada de variáveis dinâmicas e multi-métodos seria uma das grandes contribuições da linguagem.
Variáveis dinâmicas:
Em Python as variáveis são interpretadas em runtime, ou seja, tempo de execução => o programa checa toda hora se a variável mudou e isso torna ele mais lento
Variáveis estáticas:
Em C as variáveis são fixas, e isso é visto é em tempo de compilação => precisa pensar nas variáveis e isso torna o tempo de programação mais lento
Em Julia isso é basicamente opcional, não é preciso definir as variáveis, mas é possível, e elas podem mudar dinamicamente, em tempo de execução. E ainda, Julia se utiliza de multi-métodos para não ter que lidar com a constante checagem dos tipos das variáveis, como Python faz!
Despacho único:
Em geral, em linguagens de programação funções podem ter o mesmo nome, portanto deve existir algum mecanismo que irá realizar o despacho da chamada de tais funções, resolvendo o conflito dos nomes iguais.
Na maioria das linguagens de programação populares (python, C++, javascript, C#), o despacho da chamada de funções ocorre apenas levando em consideração o primeiro argumento da mesma, tal mecanismo é chamado de despacho único. Como exemplo, vamos considerar o seguinte exemplo em python
class MyClass1:
def some_function(self, a):
print("Value-1:", a)
class MyClass2:
def some_function(self, a):
print("Value-2:", a)
my_obj_1 = MyClass1()
my_obj_2 = MyClass2()
Existem duas funções com o nome some_function, e obviamente tentar chamá-las dessa forma some_function("some_text") não funciona. A chamada correta é feita da seguinte forma:
my_obj_1.some_function("some_text"): Executa a função emMyClass1.my_obj_2.some_function("some_text"): Executa a função emMyClass2
A sintaxe para chamar funções my_obj.some_function(...) é apenas o padrão adotado pelo python, mas ela é equivalente a some_function(my_obj, ...) , ou seja, quem determina qual função é de fato executada, é o primeiro argumento da chamada, os demais argumentos não são levados em consideração no momento do despacho.
Despacho múltiplo:
Em Julia, o despacho da execução de funções leva em consideração todos os seus argumentos, não apenas o primeiro, esse mecanismo leva o nome de despacho múltiplo. Para ilustrar o despacho múltiplo em ação, considere que estamos trabalhando em um código de dinâmica de partículas, e estamos precisando escrever uma função para calcular a energia potencial do sistema, que depende das massas, então podemos implementar a seguinte função
function potencial_energy(mass, positions, pars)
println("Calculando energia potencial")
end
em que
- mass: Massas das partícula.
- positions: Posições das partículas.
- pars: Parâmetros do potencial em questão.
mas suponha que agora estamos interessados em explorar o sistemas quando todas as massas são iguais, e desejamos usar essa condição para melhorar o desempenho do cálculo da energia potencial. Poderíamos adicionar algumas estruturas condicionais dentro da função acima para isso, mas uma melhor forma é fazer com que a função potencial_energy despache no argumento mass, então, precisamos criar um tipo que represente massas iguais, que apenas vai possui um único atributo (a massa comum a todas as partículas) e um novo método para potencial_energy que despacha utilizando esse tipo:
struct SameMass
masss::Float64
end
function potencial_energy(mass::SameMass, positions, pars)
println("Calculando energia potencial com otimização para massas iguais")
end
Esse novo método possui uma implementação otimizada para o caso em que todas as massas são iguais. Nada precisa mudar no código que chama potencial_energy, pois o despacho múltiplo vai fazer com que seja executado a implementação correta.
Agora suponha que estamos interessado em outro potencial (Potencial2), ao invés de criar uma nova função para Potencial2, vamos fazer com que potencial_energy despache no argumento pars
struct Potencial2
par1::Int
par2::Float64
end
function potencial_energy(mass, positions, pars::Potencial2)
println("Calculando energia potencial para Potencial2")
end
Ainda, podemos fazer um método para Potencial2 que é otimizado para todas as massas iguais
function potencial_energy(mass::SameMass, positions, pars::Potencial2)
println(""Calculando energia potencial com otimização para massas iguais para Potencial2")
end
Agora que estamos trabalhando com dois potencias, é inteligente também criar um tipo para o primeiro potencial, que vamos chamar de Potencial1:
struct Potencial1
par1::Float64
par2::Float64
end
O seguinte exemplo utiliza os métodos que criamos
positions = [] # Suponha que as posições das partículas estejam aqui
pars_1 = Potencial1(3.14, 2.71)
pars_2 = Potencial2(137, 3.48)
mass = [] # Suponha que as diferentes massas das partículas estejam aqui
same_mass = SameMass(1)
potencial_energy(mass, positions, pars_1)
potencial_energy(mass, positions, pars_2)
potencial_energy(same_mass, positions, pars_1)
potencial_energy(same_mass, positions, pars_2)
executando, temos a seguinte saída:
Calculando energia potencial Calculando energia potencial para Potencial2 Calculando energia potencial com otimização para massas iguais Calculando energia potencial com otimização para massas iguais para Potencial2
Performance de Julia: na prática
Para resumir, temos:
Python => dynamic (variáveis dinâmicas) single dispatch (métodos únicos)
C++ => static (variáveis estáticas) single dispatch
Julia => dynamic multiple dispatch
Na prática, é mostrado abaixo um exemplo da performance de Julia como linguagem de programação em dynamic multiple dispatch.
O mesmo programa foi escrito em Julia e em C++.
Em Julia:
abstract type Animal end
struct Cachorro <: Animal
nome::String
end
struct Gato <: Animal
nome::String
end
# Função de encontro que recebe tipo genérico de animal
function encontroDeAnimais(a::Animal, b::Animal)
acao = encontro(a,b)
println("$(a.nome) encontra $(b.nome) e $acao")
end
# Funções de expressão única que recebem diferentes tipos de animais
encontro(a::Cachorro, b::Cachorro) = "cheira"
encontro(a::Cachorro, b::Gato) = "persegue"
encontro(a::Gato, b::Gato) = "lambe"
encontro(a::Gato, b::Cachorro) = "ignora"
# Instanciando os bichinhos
gato1 = Gato("Luciene Maria")
gato2 = Gato("Mel")
cachorro1 = Cachorro("Batata")
cachorro2 = Cachorro("Snoopy")
# Chamando função encontroDeAnimais
encontroDeAnimais(gato1, gato2)
encontroDeAnimais(gato1, cachorro2)
encontroDeAnimais(cachorro1, cachorro2)
Em C++:
#include <iostream>
using namespace std;
class Animal {
public:
string nome;
};
string encontro(Animal a, Animal b) {}
// Função de encontro que recebe tipo genérico de animal
void encontroDeAnimais(Animal a, Animal b) {
string acao = encontro(a,b);
cout << a.nome << " encontra " << b.nome << " e " << acao << endl;
}
class Cachorro:public Animal {};
class Gato:public Animal {};
// Funções de expressão única que recebem diferentes tipos de animais
string encontro(Cachorro a, Cachorro b) { return "cheira"; }
string encontro(Cachorro a, Gato b) { return "persegue"; }
string encontro(Gato a, Gato b) { return "lambe"; }
string encontro(Gato a, Cachorro b) { return "ignora"; }
int main() {
// Instanciando os bichinhos
Gato gato1; gato1.nome = "Luciene Maria";
Gato gato2; gato2.nome = "Mel";
Cachorro cachorro1; cachorro1.nome = "Batata";
Cachorro cachorro2; cachorro2.nome = "Snoopy";
// Chamando função encontroDeAnimais
encontroDeAnimais(gato1, gato2);
encontroDeAnimais(gato1, cachorro2);
encontroDeAnimais(cachorro1, cachorro2);
return 0;
}
Para Julia nós obtemos o seguinte resultado:
Luciene Maria encontra Mel e lambe Luciene Maria encontra Snoopy e ignora Batata encontra Snoopy e cheira
Para C++ o resultado é:
Luciene Maria encontra Mel e Falha de Segmentação
Isso acontece porque C++ não aceita que uma função utilize-se de uma variável sem antes saber qual o tipo dessa variável! Por isso, poder utilizar-se de variáveis dinâmicas quando há multi-métodos é um diferencial que acaba por incrementar a performance de Julia como linguagem de programação visada para o Cálculo Numérico.
Observação: é importante ressaltar que os testes feitos não são conclusivos para debater a performance de Julia, em termos estatísticos, e além disso, ser uma linguagem de programação que utiliza de variáveis dinâmicas e multi-métodos não é o único motivo pelo qual Julia poderia trazer tal performance em Cálculo Numérico. Podemos ainda contar com a sua capacidade de metaprogramação, ou seja, Julia pode usar macros e eles são aplicados em tempo de interpretação. Há ainda outros fatores da construção da linguagem que contribuem para sua performance que aqui não foram citados.
Aprendendo Julia
Ambiente de programação
Após feita a instalação de Julia, para abri-la no seu terminal de comando é preciso apenas digitar:
$julia
para entrar em seu ambiente de programação.
É possível, também, programar em um arquivo de texto (salvo como .jl) e executar o programa pelo terminal, fazendo simplesmente:
$julia programa.jl
Impressão na tela
println("Hello World")
Saída:
Hello World
Variáveis
Variáveis são atribuídas dinamicamente e podem mudar.
s = 1 s = "Oi" println(s) println(typeof(s)) Saída: Oi String
s::String s = 1 println(s) Saída: TypeError: in typeassert, expected String, got Int32
Condicionais
cats = 12
if cats < 1
println("You should adopt a cat.")
elseif cats >= 1 && cats <=6
println("Not enough cats.")
elseif cats >= 7 && cats <= 12
println("Still not enough cats.")
else
println("Gato have more cats.")
end
Saída:
Still not enough cats.
i = 0 while (i < 10) global i += 1 println(i) end Saída: 1 2 3 4 5 6 7 8 9 10
for i = 1:10 println(i) end Saída: 1 2 3 4 5 6 7 8 9 10
for i in [1,2,3] println(i) end Saída: 1 2 3
Arrays
# Criando um array de zeros a1 = zeros() println(a1) # Posso definir o tipo e o tamanho do Array (linhas, colunas) também a1 = zeros(Int32, 1, 4) println(a1) Saída: 0.0 [0 0 0 0]
# Criando um array do tipo inteiro
a2 = Array{Int32}
println(a2)
# Criando um array (de outra maneira) do tipo float
a3 = Float64[]
println(a3)
Saída:
Array{Int32,N} where N [...]
Float64[]
# Criando um array e definindo valores
a4 = [1,2,3]
#Imprimindo a4
println("Array: ", a4)
Saída:
Array: [1, 2, 3]
a4 = [1,2,3]
# Imprimindo valor de um indíce específico
println("Imprimindo primeiro elemento: ", a4[1])
# Imprimindo último valor do array
println("Imprimindo último elemento: ",a4[end])
Saída:
Imprimindo primeiro elemento: 1
Imprimindo último elemento: 3
a4 = [1,2,3] println(a4[2]) # Valores podem mudar (diferente de Tuplas, que veremos adiante) a4[2] = 4 println(a4[2]) Saída: 2 4
a4 = [1,2,3]
println(a4)
# Número de elementos
println("Imprimindo número de elementos: ",length(a4))
Saída:
[1, 2, 3]
Imprimindo número de elementos: 3
a4 = [1,2,3]
# Soma os valores do array
println("Imprimindo soma dos elementos: ",sum(a4))
# Põe os valores começando no índice 2
splice!(a4, 2:1, [8,9])
println("Imprimindo Array tendo feito splice!(a4, 2:1, [8,9]): ",a4)
# Remove os itens do índice 2 ao 3
4splice!(a4, 2:3)
println("Imprimindo Array tendo feito splice!(a4, 2:3): ",a4)
Saída:
Imprimindo soma dos elementos: 6
Imprimindo Array tendo feito splice!(a4, 2:1, [8,9]): [1, 8, 9, 2, 3]
Imprimindo Array tendo feito splice!(a4, 2:3): [1, 2, 3]
a4 = [1,2,3]
# Pegar valor máximo e valor mínimo
println("Imprimindo valor máximo: ",maximum(a4))
println("Imprimindo Array valor mínimo: ",minimum(a4))
# Multiplicando todos os elementos do array por outro número sem precisar de um for
println("Imprimindo multiplicação dos elementos por 2: ",a4 * 2)
Saída:
Imprimindo valor máximo: 3
Imprimindo Array valor mínimo: 1
Imprimindo multiplicação dos elementos por 2: [2, 4, 6]
# Arrays podem conter funções a5 = [sin, cos, tan] for n in a5 println(n(0)) end Saída: 0.0 1.0 0.0
# Para os acostumados com range a6 = collect(1:5) println(a6) Saída: [1, 2, 3, 4, 5]
Tuplas
A maioria das funções de array funciona com tuplas.
# Valores não podem mudar
t1 = (1,2,3,4)
println(t1[2])
t1[2] = 5
println(t1[2])
Saída:
2
MethodError: no method matching setindex!(::NTuple{4,Int32}, ::Int32, ::Int32)
# Imprimindo a tupla inteira println(t1) # Imprimindo a tupla inteira for i in t1 println(i) end Saída: (1, 2, 3, 4) 1 2 3 4
Dicionários
A palavra-chave deve ser única.
d1 = Dict("pi"=>3.14, "e"=>2.718)
# Imprimir um valor
println(d1["pi"])
Saída:
3.14
d1 = Dict("pi"=>3.14, "e"=>2.718)
# Imprimindo todas as palavras-chaves
println(keys(d1))
# Imprimindo todos os valores
println(values(d1))
# Adicionar uma palavra-chave
d1["golden"] = 1.618
# Deleter uma palavra-chave
delete!(d1, "pi")
# Imprimindo todas as palavras-chaves
println(keys(d1))
# Imprimindo todos os valores
println(values(d1))
Saída:
["pi", "e"]
[3.14, 2.718]
["e", "golden"]
[2.718, 1.618]
d1 = Dict("pi"=>3.14, "e"=>2.718)
# Ver se a palavra-chave existe
println(haskey(d1, "pi"))
# Imprimindo palavras-chaves E valores
for kv in d1
println(kv)
end
Saída:
true
"pi" => 3.14
"e" => 2.718
Sets
Sets são arrays com elementos únicos.
st1 = Set(["Jim", "Pam", "Jim"]) # Ele não pega os elementos repetidos println(st1) Saída: Set(["Pam", "Jim"])
st1 = Set(["Jim", "Pam", "Jim"])
# Adicionando um elemento
push!(st1, "Michael")
println(st1)
# Ver se um elemento está no Set
println(in("Dwight", st1))
Saída:
Set(["Pam", "Michael", "Jim"])
false
st1 = Set(["Jim", "Pam", "Jim"]) st2 = Set(["Stanley", "Meredith"]) # Combinando Sets println(union(st1, st2)) # Imprimindo todo o elemento que os dois Sets tem em comum println(intersect(st1, st2)) # Imprimindo elementos que estão no primeiro Set, mas não no segundo println(setdiff(st1, st2)) Saída: Set(["Jim", "Meredith", "Stanley", "Pam"]) Set(String[]) Set(["Pam", "Jim"])
Funções
using Printf
# Função de expressão única
soma(x,y) = x + y
x, y = 1, 2
@printf("%d + %d = %d\n", x, y, x+y)
Saída:
1 + 2 = 3
# Função de múltiplas expressões
function adoptACat(cats)
if cats <= 1
println("You should adopt a cat.")
else
println("You should adopt a cat. They're cute.")
end
end
adoptACat(2)
Saída:
You should adopt a cat. They're cute.
v1 = 5 function changeV1(v1) v1 = 10 end changeV1(v1) println(v1) Saída: 5
v1 = 5 function changeV1(v1) v1 = 10 return v1 end changeV1(v1) println(v1) v2 = changeV1(v1) println(v2) Saída: 5 10
# Usando variáveis globais dentro da função v1 = 5 function changeV12() global v1 = 10 end changeV12() println(v1) Saída: 10
# Quando não sei quantos argumentos vou passar function soma(args...) sum = 0 for i in args sum += i end println(sum) end soma(1,2,3) Saída: 6
# Retornando mais de um valor function retorna2(valor) return (valor + 1, valor + 2) end println(retorna2(4)) Saída: (5, 6)
# Map é uma função anônima que aplica uma função para cada elemento v = map(x -> x * x, [1,2,3]) println(v) Saída: [1, 4, 9]
Structs
struct Estudante
name::String
saldoTRI::Float32
cartaoUFRGS::Int
end
# Criando um objeto
estudante1 = Estudante("Raquel", 10.50, 244449)
println(estudante1.name, "\n", estudante1.saldoTRI, "\n", estudante1.cartaoUFRGS)
Saída:
Raquel
10.5
244449
Tipos Abstratos
Tipos abstratos não podem ser instanciados como as Structs (instanciar => fazer estudante1 = Estudante(“Raquel”, 10.50, 244449) => criar um objeto) MAS podem ter subTipos e isso é muito útil!
abstract type animal end
struct cachorro <: animal
nome::String
latido::String
end
struct gato <: animal
nome::String
miado::String
end
cachorro1 = cachorro("Urso", "Au Au")
gato1 = gato("Lucia Irene", "Miau")
# Criando funções pros subTipos
function fazerSom(animal::cachorro)
println("$(animal.nome) diz $(animal.latido)")
end
function fazerSom(animal::gato)
println("$(animal.nome) diz $(animal.miado)")
end
fazerSom(cachorro1)
fazerSom(gato1)
Saída:
Urso diz Au Au
Lucia Irene diz Miau
Modularizando códigos em Julia
Módulos
Na Julia é possível agrupar pedaços de códigos em módulos, cuja função é puramente de organização. Módulos são definidos pela palavra-chave `module` e eles introduzem um novo escopo, por exemplo:
module MyModule
struct SomeStruct
some_attr::Float64
end
function sum(a ,b)
println(a + b)
end
function product(a ,b)
println(a * b)
end
end
Para acessar o conteúdo dos módulos fora deles, é necessário qualificar o nome do item de interesse, por exemplo, podemos utilizar a função `sum` da seguinte forma:
module MyModule
...
end
function main()
MyModule.sum(1, 3)
end
main()
Em python, cada arquivo .py é um módulo, em Julia não existe esse conceito, um arquivo .jl pode conter diversos módulos e um módulo pode estar espalhado em diversos arquivos.
- Mais informações sobre módulos podem ser encontradas no manual da Julia
Separando o código em arquivos
A Julia não possui o conceito de código em diferentes arquivos, assim como é no python por exemplo (cada arquivo é um módulo), mas podemos, apenas por questão de conveniência, separar o código em diferentes arquivos, no entanto um deles vai ser o arquivo principal, e seu dever e incluir todos os outros arquivos utilizando o comando `include`.
Criando pacotes
Vamos criar um pacote que pode ser utilizado em qualquer lugar em sua máquina (utilizando using MyPkgName), para isso navegue para o local em que se deseja color os arquivos do pacote, abra um REPL e execute
using PkgTemplate
t = Template(dir=".")
t("MyPkg")
Isto irá automaticamente criar uma pasta contendo os arquivos do pacote na localização atual. Para podermos utilizá-lo em qualquer lugar, precisamos adicioná-lo no ambiente atual, que pode ser feito da seguinte forma:
- Utilizando o mesmo REPL que foi utilizado para criar o pacote, entre no modo de gerenciamento de pacotes (aparte ] com a entrada do REPL vazia)
- Execute o comanndo
pkg> activate MyPkg
a partir de agora, qualquer arquivo pode utilizar
using MyPkg
- Para mais informações sobre como gerenciar/criar pacotes em julia, clique aqui.
- Para mais informações sobre como criar pacotes com o PkgTemplate, clique aqui.



![{\displaystyle f_{j}^{n+1}=f_{j}^{n}+D{\frac {dt}{(dx)^{2}}}[f_{j+1}^{n}+f_{j-1}^{n}-2f_{j}^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b7f6e49593597da54a759c57f0bd9f6997f1ac7)
