Equação de Ginzburg-Landau complexa: mudanças entre as edições
| Linha 19: | Linha 19: | ||
== Dedução == | == Dedução == | ||
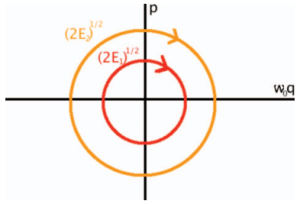
[[File:Phase_space_circle.png|right|Espaço de fase do oscilador harmônico]] | [[File:Phase_space_circle.png|thumb|right|Espaço de fase do oscilador harmônico]] | ||
A energia de um oscilador harmônico é expressa pela equação abaixo, onde <math>E</math> é a energia, <math>q</math> e <math>p</math> a coordenada e seu respectivo momento, <math>m</math> é a massa e <math>\omega_0</math> a frequência angular | A energia de um oscilador harmônico é expressa pela equação abaixo, onde <math>E</math> é a energia, <math>q</math> e <math>p</math> a coordenada e seu respectivo momento, <math>m</math> é a massa e <math>\omega_0</math> a frequência angular | ||
Edição das 13h39min de 27 de abril de 2024
A equação de Ginzburg-Landau complexa (CGLE) surgiu inicialmente em 1969 como um modelo para o inicio de instabilidades em problemas de convecção de fluídos. A partir de então, ela se tornou uma das equações não lineares mais estudadas da física, descrevendo uma variedade enorme de fenômenos como:
- Ondas não lineares;
- Transições de fase de segunda ordem;
- Supercondutividade;
- Superfluidez;
- Condensado de Bose-Einstein.
A equação de Ginzburg-Landau complexa, quando escrita de modo a minimizar o número de constantes, é dada pela equação abaixo:
É possível deduzir a CGLE a partir do oscilador linear harmônico por meio de argumentos de simetria, encontrando a equação de Stuart-Landau, e, em seguida, considerando um sistema estendido no espaço.
Dedução
A energia de um oscilador harmônico é expressa pela equação abaixo, onde é a energia, e a coordenada e seu respectivo momento, é a massa e a frequência angular
Ao realizar as seguintes mudanças de variáveis, e , a equação da energia produz trajetórias circulares no espaço de fase de e