O sistema
O exemplo a ser considerado é da biologia matemática, muitas ferramentas matemáticas utilizado na dinâmica de populações encontra-se também na dinâmica de epidemias. O objetivo deste tópico não é se aprofundar na modelagem em si, mas a utilizar como motivação para compreender melhor os sistemas de equações diferenciais com atraso baseado no artigo "Oscillations in SIRS model with distributed delays".
Uma doença do tipo SIRS é caracterizada por um tempo de infecção  e um tempo de imunidade
e um tempo de imunidade  . Isto é, um indivíduo que se infecte em um tempo
. Isto é, um indivíduo que se infecte em um tempo  vai deterministicamente se recuperar em um tempo
vai deterministicamente se recuperar em um tempo  , tornando-se temporariamente imune por um tempo
, tornando-se temporariamente imune por um tempo  . Então no instante
. Então no instante  perde a imunidade tornando-se suscetível novamente. Este sistema pode ser representado por um conjunto de equações para a fração de população infecciosa (e infectada)
perde a imunidade tornando-se suscetível novamente. Este sistema pode ser representado por um conjunto de equações para a fração de população infecciosa (e infectada)  e suscetível
e suscetível  :
:


Onde  é a taxa de contágio por indivíduo. A fração da subpopulação em recuperação (imune) é dada por
é a taxa de contágio por indivíduo. A fração da subpopulação em recuperação (imune) é dada por  . O primeiro termos em ambas as equações representa o contágio dos suscetíveis pelos infecciosos, daqui em diante muitas vezes será referido como:
. O primeiro termos em ambas as equações representa o contágio dos suscetíveis pelos infecciosos, daqui em diante muitas vezes será referido como:  . Os segundos termos representam a recuperação ou a perda de imunidade após
. Os segundos termos representam a recuperação ou a perda de imunidade após  e
e  decorrido desde a infecção, respectivamente. Isto é:
decorrido desde a infecção, respectivamente. Isto é:


Em outras palavras, uma fração  se contagia no instante
se contagia no instante  , no instante
, no instante  ela se recupera, diminuindo os infecciosos. No instante
ela se recupera, diminuindo os infecciosos. No instante  ela perde a imunidade, aumentando a quantidade de suscetíveis. Estas equações exigem condições iniciais, matematicamente usualmente se fornece funções arbitrárias
ela perde a imunidade, aumentando a quantidade de suscetíveis. Estas equações exigem condições iniciais, matematicamente usualmente se fornece funções arbitrárias  e
e  no intervalo
no intervalo ![{\textstyle \left[-\tau _{0},0\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78093fef9dbf06a6b990659bd088590201247bd7) . Porém de um ponto de vista epidemiológico, é razoável prover condições iniciais em
. Porém de um ponto de vista epidemiológico, é razoável prover condições iniciais em  e dinâmicas complementares nos intervalos
e dinâmicas complementares nos intervalos  e
e  .
.
 somente contágio local. Utiliza-se as equações apenas com os primeiros termos, sem atraso.
somente contágio local. Utiliza-se as equações apenas com os primeiros termos, sem atraso. Transição do estágio de infeccioso para em recuperação, ou seja, retira-se apenas o segundo termo na equação da dinâmica dos suscetíveis.
Transição do estágio de infeccioso para em recuperação, ou seja, retira-se apenas o segundo termo na equação da dinâmica dos suscetíveis.
E com as condições iniciais:

Ponto de equilíbrio
Para análise dos pontos de equilíbrio uma representação integral é uma forma melhor forma de representar o sistema, pois se fizermos algo análogo ao que foi feito em Equações diferenciais com atrasos, não será possível obter nenhuma informação sobre o ponto de equilíbrio, pois aparentemente qualquer par de valores poderia representar um ponto de equilíbrio. Para a dinâmica dos infecciosos é proposto então:

A interpretação é direta, integra-se sobre sobre todos os indivíduos que se contagiaram entre o tempo  e
e  . Estes serão os infecciosos no instante
. Estes serão os infecciosos no instante  , uma vez que todos infectados anteriormente a este tempo já estarão recuperados. A constante de integração
, uma vez que todos infectados anteriormente a este tempo já estarão recuperados. A constante de integração  a princípio é arbitrária, mas espera-se que
a princípio é arbitrária, mas espera-se que  pois não deve haver outras fontes de infecções adicionais. Complementariamente:
pois não deve haver outras fontes de infecções adicionais. Complementariamente:

Pelo lado esquerdo, pode-se perceber ver que isto se refere a população que não está se recuperando, isto é  , ou seja, os infectados e suscetíveis. A integral cobre os contágios que ocorreram durante
, ou seja, os infectados e suscetíveis. A integral cobre os contágios que ocorreram durante  anterior. Desta forma, esta integral fornece o número de pessoas que estão no período de recuperação, logo é razoável supor que
anterior. Desta forma, esta integral fornece o número de pessoas que estão no período de recuperação, logo é razoável supor que  uma vez que também não há outras fontes de pessoas em recuperação. Para um estado de equilíbrio então que a fração de contagiados em um instante
uma vez que também não há outras fontes de pessoas em recuperação. Para um estado de equilíbrio então que a fração de contagiados em um instante  qualquer é constante, pode-se escrever
qualquer é constante, pode-se escrever  . Para
. Para  :
:

E para  , de maneira análoga:
, de maneira análoga:

Uma vez que  . Lembrando que
. Lembrando que  , então no estado de equilíbrio
, então no estado de equilíbrio  , denotando os pontos de equilíbrio apenas como
, denotando os pontos de equilíbrio apenas como  e
e  , obtém-se do primeiro resultado:
, obtém-se do primeiro resultado:

E do segundo:

Assim o ponto de equilíbrio é:  .
.
Validade da aproximação e sistema de equações sem atraso
Uma atenção especial deve ser dada a consideração de que  quando foi proposto a equação integral para
quando foi proposto a equação integral para  . A formulação matemática do modelo sem atraso é usualmente escrito como:
. A formulação matemática do modelo sem atraso é usualmente escrito como:

Integrando a equação da dinâmica de  do sistema sem atraso, de
do sistema sem atraso, de  a
a  , obtém-se:
, obtém-se:
![{\displaystyle {\begin{aligned}{\frac {di\left(t\right)}{dt}}&=\beta s\left(t\right)i\left(t\right)-{\frac {i\left(t\right)}{\tau _{i}}}\\\int _{i\left(t^{*}-\tau _{i}\right)}^{i\left(t^{*}\right)}di&=\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt-{\frac {1}{\tau _{i}}}\int _{t^{*}-\tau _{i}}^{t^{*}}i\left(t\right)dt\\i\left(t^{*}\right)&=\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt+\left[i\left(t^{*}-\tau _{i}\right)-{\frac {1}{\tau _{i}}}\int _{t^{*}-\tau _{i}}^{t^{*}}i\left(t\right)dt\right]{eq:tri}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a453641c87483dc6419ad8f45edce081a2d2c66)
Considerando no equilíbrio que  :
:

Sendo que no equilíbrio os valores são constantes  e
e  :
:

De onde é possível obter também o mesmo ponto de equilíbrio obtido anteriormente:

Outra formar de comparar as equações, é que para obter versão integral apresentada para  a partir de::
a partir de::
![{\displaystyle i\left(t^{*}\right)=\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt+\left[i\left(t^{*}-\tau _{i}\right)-{\frac {1}{\tau _{i}}}\int _{t^{*}-\tau _{i}}^{t^{*}}i\left(t\right)dt\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c115219a9620bbe48ab9463e822f1d8324cfab7)
É é necessário que o termo entre colchete seja zerado. Isto é, considerando que no equilíbrio  e
e  sejam constantes:
sejam constantes:

Desta forma a condição imposta anteriormente é recuperada. Agora percebe-se que o ponto de equilíbrio é independente das condições iniciais, depende apenas dos parâmetros escolhidos  e
e  . Por exemplo, resolvendo numericamente o sistema de equações diferenciais proposto, com os parâmetros
. Por exemplo, resolvendo numericamente o sistema de equações diferenciais proposto, com os parâmetros  ,
,  e
e  , e condições iniciais
, e condições iniciais  , o sistema atinge o equilíbrio precisamente nos pontos calculados.
, o sistema atinge o equilíbrio precisamente nos pontos calculados.
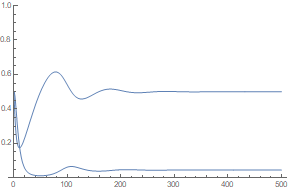
Solução numérica do sistema de equações diferenciais sem atraso obtido via Mathematica.
Além disto, pode-se verificar que  e
e  , concordando com nossos cálculos analíticos. Isto implica que no equilíbrio, a população total infecciosa em um instante
, concordando com nossos cálculos analíticos. Isto implica que no equilíbrio, a população total infecciosa em um instante  é sempre dada inteiramente pelos que foram infectados durante um período anterior
é sempre dada inteiramente pelos que foram infectados durante um período anterior  , ou seja, a área dada pelo retângulo de largura
, ou seja, a área dada pelo retângulo de largura  e altura
e altura  , uma vez que no equilíbrio as frações
, uma vez que no equilíbrio as frações  e
e  são constantes. Estes resultados concordam com a suposição de que
são constantes. Estes resultados concordam com a suposição de que  .
.
Porém tentando o mesmo procedimento para a equação com atraso, obtém-se:
![{\displaystyle {\begin{aligned}{\frac {di\left(t\right)}{dt}}=&\beta s\left(t\right)i\left(t\right)-\beta s\left(t-\tau _{i}\right)i\left(t-\tau _{i}\right)\\\int _{i\left(t^{*}-\tau _{i}\right)}^{i\left(t^{*}\right)}di=&\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt-\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t-\tau _{i}\right)i\left(t-\tau _{i}\right)dt\\i\left(t^{*}\right)=&\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt+\left[i\left(t^{*}-\tau _{i}\right)-\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t-\tau _{i}\right)i\left(t-\tau _{i}\right)dt\right]{eq:cat}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd8a500d717706c37e14bf29bc0311f60d2da7ab)
Utilizando a consideração  , é possível obter apenas
, é possível obter apenas  . Para recuperar a equação original seria necessário que, de modo análogo a equação sem atraso, a seguinte igualdade fosse válida:
. Para recuperar a equação original seria necessário que, de modo análogo a equação sem atraso, a seguinte igualdade fosse válida:

Isto é, de modo análogo ao caso anterior, que no equilíbrio a fração de infecciosos em um tempo  seja dado inteiramente pelos que foram contagiados em um tempo
seja dado inteiramente pelos que foram contagiados em um tempo  . Porém neste caso qualquer par de pontos
. Porém neste caso qualquer par de pontos  poderia consistir em um ponto de equilíbrio para um conjunto de parâmetros
poderia consistir em um ponto de equilíbrio para um conjunto de parâmetros  qualquer. A dependência se torna das condições iniciais. Utilizando por exemplo condições iniciais constantes como frequentemente é utilizado na literatura de equações com atraso, a própria condição inicial se torna um ponto de equilíbrio
qualquer. A dependência se torna das condições iniciais. Utilizando por exemplo condições iniciais constantes como frequentemente é utilizado na literatura de equações com atraso, a própria condição inicial se torna um ponto de equilíbrio  . Pode-se pensar que desta fração
. Pode-se pensar que desta fração  de infecciosos , a cada instante
de infecciosos , a cada instante  , uma quantidade de
, uma quantidade de  de infecciosos são curados, porém outra quantidade igual
de infecciosos são curados, porém outra quantidade igual  de suscetíveis são infectados, mantendo a taxa de variação zerada e a quantidade total de infecciosos constante. Assim sendo, pensando em situações reais, para um instante
de suscetíveis são infectados, mantendo a taxa de variação zerada e a quantidade total de infecciosos constante. Assim sendo, pensando em situações reais, para um instante  , há quantidade
, há quantidade  da fração que permanece infecciosa mesmo após
da fração que permanece infecciosa mesmo após  , que soma-se aos novos infectados, mantendo a fração constante. Isto é, para a equação:
, que soma-se aos novos infectados, mantendo a fração constante. Isto é, para a equação:

Então  . Para retirar esta constante, pode-se pensar que é como se no equilíbrio precisasse de
. Para retirar esta constante, pode-se pensar que é como se no equilíbrio precisasse de

tempo para que uma pessoa infecciosa se curasse, ao invés de

. Pois após

tempo toda a população

terá sido substituída por uma nova população infecciosa isto é

, uma vez que a cada instante

tem-se que uma fração

da população suscetível sendo infectada, e outra fração

da população infecciosa que se recuperou pois foi infectada em um instante anterior

. . Reescrevendo a integral com este novo limite

Uma vez que  para estas condições iniciais. Além disto, a expressão para
para estas condições iniciais. Além disto, a expressão para  é análoga a equação encontrada para o ponto de equilíbrio do sistema sem atraso, isto é
é análoga a equação encontrada para o ponto de equilíbrio do sistema sem atraso, isto é  . Toda discussão foi feita para condições iniciais constantes, quando se utiliza o método proposto, a análise torna-se mais complicada, mas ainda é notável que o ponto de equilíbrio depende das condições iniciais.Utilizando o conjunto de parâmetros
. Toda discussão foi feita para condições iniciais constantes, quando se utiliza o método proposto, a análise torna-se mais complicada, mas ainda é notável que o ponto de equilíbrio depende das condições iniciais.Utilizando o conjunto de parâmetros  ,
,  e
e  , para diferentes valores iniciais é possível obter:
, para diferentes valores iniciais é possível obter:
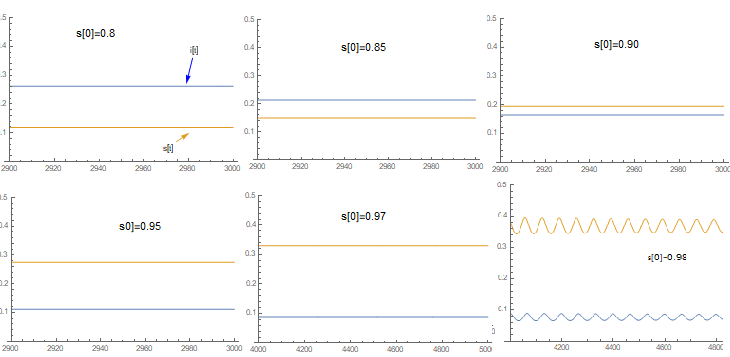
Solução em equilíbrio do sistema de equações diferenciais com atraso para diferentes valores iniciais de infecciosos.
Pode-se notar que aproximadamente:
Lembrando da integral proposta para a condição de equilíbrio condição de equilíbrio:

Novamente  , mais especificamente
, mais especificamente  . Este resultado faz sentido, pois de acordo com o procedimento proposto, não há momento em que os infecciosos iniciais
. Este resultado faz sentido, pois de acordo com o procedimento proposto, não há momento em que os infecciosos iniciais  se recuperam. Durante o tempo
se recuperam. Durante o tempo  uma fração da população se infecta, e então esta mesma fração começa a se recuperar após
uma fração da população se infecta, e então esta mesma fração começa a se recuperar após  , mas os infecciosos iniciais, nunca se recuperam, funcionando como fontes permanentes de infecção. Outra forma de comparar, é que olhando o conjunto de equações diferenciais originais o termo responsável pela recuperação dos infecciosos no instante
, mas os infecciosos iniciais, nunca se recuperam, funcionando como fontes permanentes de infecção. Outra forma de comparar, é que olhando o conjunto de equações diferenciais originais o termo responsável pela recuperação dos infecciosos no instante  depende da quantidade total de infecciosos no próprio instante
depende da quantidade total de infecciosos no próprio instante  . No conjunto de equações com atraso, é a fração da população da população que foi contagiada em um instante anterior. Ou seja, uma fração da população que se infectou em um instante
. No conjunto de equações com atraso, é a fração da população da população que foi contagiada em um instante anterior. Ou seja, uma fração da população que se infectou em um instante  , é a mesma que se recuperara em um instante posterior
, é a mesma que se recuperara em um instante posterior  , porém a quantidade inicial de infecciosos não se contagiou em nenhum momento desta ’linha do tempo', então também não se recuperam em nenhum momento.
, porém a quantidade inicial de infecciosos não se contagiou em nenhum momento desta ’linha do tempo', então também não se recuperam em nenhum momento.
Porém ainda que  , quanto mais próximo a população inicial de infecciosos for de
, quanto mais próximo a população inicial de infecciosos for de  , melhor será aproximação, Por isso a análise em torno do ponto de equilíbrio, e o próprio ponto de equilíbrio se torna uma aproximação válida apenas quando é adotado valores próximos de
, melhor será aproximação, Por isso a análise em torno do ponto de equilíbrio, e o próprio ponto de equilíbrio se torna uma aproximação válida apenas quando é adotado valores próximos de  para
para  .
.
Análise do ponto de equilíbrio
Obtendo a equação transcendental
Aplicando então uma perturbação nos pontos de equilíbrios, isto é:  e
e 
 pode-se obter uma aproximação linear em torno do ponto de equilíbrio (uma observação é que o teste utilizando os limites leva a uma indeterminação, uma vez que não há termo linear). Então analisando o termo que chamamos de contágios:
pode-se obter uma aproximação linear em torno do ponto de equilíbrio (uma observação é que o teste utilizando os limites leva a uma indeterminação, uma vez que não há termo linear). Então analisando o termo que chamamos de contágios:

Ignorando os termos não lineares e denotando  e
e  :
:

Tem-se então:

E:

O sistema linearizado em torno do ponto de equilíbrio é então:

Reescrevendo matricialmente:

Ou ainda:

A equação característica para um sistema do tipo:

É dado por:
![{\displaystyle \det \left[\Delta \left(\lambda \right)\right]=\det \left[\lambda \mathbb {I} -A_{0}-\sum _{i=1}^{k}A_{i}e^{-\lambda T_{i}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af165a4947325d8223f3e6bc9dbe57c2acfbe569)
A função  é chamada de quase-polinômio característico. Como de costume, se para para todo
é chamada de quase-polinômio característico. Como de costume, se para para todo  , for
, for  o sistema é assintoticamente estável.
o sistema é assintoticamente estável.
Detalhes:
- Se não houver atraso, a equação é reduzida a
![{\textstyle \det \left[\lambda \mathbb {I} -A_{0}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/385c1cfaf89279b436eb62e91a64e45625af1385) . Como para achar as raízes deve-se fazer
. Como para achar as raízes deve-se fazer ![{\textstyle \det \left[\Delta \left(\lambda \right)\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b6401e8e0b97bad294469d0bcb08e63a3cdd426) , obtém-se o resultado tradicional.
, obtém-se o resultado tradicional.
- Se houver apenas uma equação, e não um sistema, então os termos
 serão constantes e não uma matrizes. Substituindo
serão constantes e não uma matrizes. Substituindo  :
:

Então:

Obtém-se o quase-polinômio característico proposto pro sistema conforme. Dessa forma, a equação transcendental característica para o sistema que estamos interessados é:
![{\displaystyle {\begin{aligned}\det \left[\Delta \left(\lambda \right)\right]=&\det \left[\lambda \mathbb {I} -A_{0}-A_{1}e^{-\lambda \tau _{0}}-A_{2}e^{-\lambda \tau _{i}}\right]\\=&\det \left[\left({\begin{array}{cc}\lambda &0\\0&\lambda \end{array}}\right)-\beta \left({\begin{array}{cc}-i^{*}&-s^{*}\\i^{*}&s^{*}\end{array}}\right)-\beta \left({\begin{array}{cc}i^{*}&s^{*}\\0&0\end{array}}\right)e^{-\lambda \tau _{0}}+\beta \left({\begin{array}{cc}0&0\\i^{*}&s^{*}\end{array}}\right)e^{-\lambda \tau _{i}}\right]\\=&\det \left[\left({\begin{array}{cc}\lambda +\beta i^{*}\left(1-e^{-\lambda \tau _{0}}\right)&\beta s^{*}\left(1-e^{-\lambda \tau _{0}}\right)\\\beta i^{*}\left(e^{-\lambda \tau _{i}}-1\right)&\lambda +\beta \left(e^{-\lambda \tau _{i}}-1\right)s^{*}\end{array}}\right)\right]\\=&\left[\lambda +\beta i^{*}\left(1-e^{-\lambda \tau _{0}}\right)\right]\left[\lambda +\beta \left(e^{-\lambda \tau _{i}}-1\right)s^{*}\right]-i^{*}\beta \left(e^{-\lambda \tau _{i}}-1\right)s^{*}\beta \left(1-e^{-\lambda \tau _{0}}\right)\\=&\lambda ^{2}+\lambda \beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]+\beta ^{2}s^{*}i^{*}\left(e^{-\lambda \tau _{i}}-1\right)\left(1-e^{-\lambda \tau _{0}}\right)-\beta ^{2}s^{*}i^{*}\left(e^{-\lambda \tau _{i}}-1\right)\left(1-e^{-\lambda \tau _{0}}\right)\\=&\lambda ^{2}+\lambda \beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cd8f17768c479c7e3a2cbc539ed13c67fdf6f38)
Para encontrar as raízes
![{\displaystyle {\begin{aligned}\lambda ^{2}+\lambda \beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/757b2f6a0a8648034d3949191c4098ae1acb152f)
Esta equação é chamada de equação característica transcendental. Uma raiz é  , e a outra pode ser obtida a partir de:
, e a outra pode ser obtida a partir de:
![{\displaystyle {\begin{aligned}\lambda +\beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdf78f7b306aa827762fa0b596e14ff81918e685)
Como uma raiz é  , se
, se  há um equilíbrio instável próximo ao ponto de equilíbrio.
há um equilíbrio instável próximo ao ponto de equilíbrio.
- Observações:
- Equação transcendental: equação que contém uma função transcendental da variável que deve ser resolvida.
- Função transcendental: função que não satisfaz uma equação polinomial, em contraste com uma função algébrica, isto é, transcende a álgebra”. Um exemplo é a função exponencial.
- Função algébrica: função que pode ser definida como a raiz de uma equação polinomial.
Soluções aproximadas são obtidas por métodos gráficos conforme feito anteriormente para soluções reais em Equações diferenciais com atrasos, ou até simplesmente observando o gráfico. Mas neste caso será utilizado algoritmos.
Obtendo as raízes da equação transcendental
Método de Newton
Também conhecido como método de Newton-Raphson, aproxima a função com uma linha. Esta linha atravessa o ponto  e tem inclinação igual a derivada da própria função. Matematicamente isto é:
e tem inclinação igual a derivada da própria função. Matematicamente isto é:

Então encontra-se o  que atravessa o eixo e o utiliza como uma nova tentativa. Ou seja o segundo ponto sobre a reta é
que atravessa o eixo e o utiliza como uma nova tentativa. Ou seja o segundo ponto sobre a reta é  , então:
, então:

Para estender o método para o plano complexo, basta substituir variável real  por uma variável complexa
por uma variável complexa  . A partir disto, o loop é repetido.
. A partir disto, o loop é repetido.
Aplicando o método
Então sendo:
![{\displaystyle {\begin{aligned}f\left(\lambda \right)&=\lambda +\beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]\\f'\left(\lambda \right)&=1+\beta \left[\tau _{0}i^{*}e^{-\lambda \tau _{0}}-s^{*}\tau _{i}e^{-\lambda \tau _{i}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/567b36fa7c40c26cc6255397872da4c824b38e63)
Foi utilizado um algoritmo em Python para buscar as raízes complexas. O gráfico original é  . Onde
. Onde  é chamado de taxa de reprodução básica. Para facilitar foi escolhido denotar
é chamado de taxa de reprodução básica. Para facilitar foi escolhido denotar  . Com poucas manipulações é possível mostrar que:
. Com poucas manipulações é possível mostrar que:

Assim para um  constante pode-se variar apenas
constante pode-se variar apenas  e
e  . Deste modo o algoritmo proposto busca a existência de raízes com parte real positiva, isto é, o conjunto de equações apresenta comportamento instável na proximidade do ponto de equilíbrio. Esta busca ocorre para cada par de valores
. Deste modo o algoritmo proposto busca a existência de raízes com parte real positiva, isto é, o conjunto de equações apresenta comportamento instável na proximidade do ponto de equilíbrio. Esta busca ocorre para cada par de valores  na malha formada por
na malha formada por  , onde
, onde  e
e  , com intervalos de
, com intervalos de  . Especificamente em cada par de valores é executado o algoritmo de Newton-Raphson com o chute inicial partindo de cada ponto possível do plano complexo dentro da região delimitada por
. Especificamente em cada par de valores é executado o algoritmo de Newton-Raphson com o chute inicial partindo de cada ponto possível do plano complexo dentro da região delimitada por  , com espaçamento entre os pontos de
, com espaçamento entre os pontos de  . Isto ocorre enquanto nenhuma raiz com parte real positiva seja encontrada, além disso, é realizada no máximo
. Isto ocorre enquanto nenhuma raiz com parte real positiva seja encontrada, além disso, é realizada no máximo  tentativas de aproximação, e é considerado
tentativas de aproximação, e é considerado  se
se  .
.
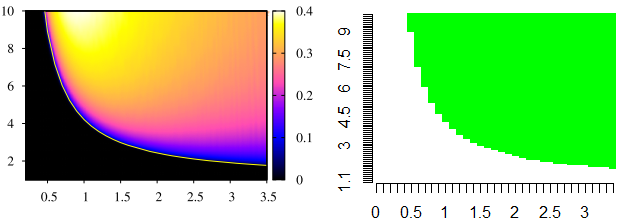
A esquerda a imagem original retirada do artigo. A região preta são soluções sem oscilação e a colorida onde há a presença de oscilações. A direita a imagem obtida através do algoritmo proposto onde a região verde indica que foi encontrado autovalores positivos.
Algoritmos
O conjunto de equações diferenciais sem atraso pode ser solucionado via Mathematica:
tmax = 400; b = 0.4; ti = 5; tr = 5;
sol = NDSolve[{
s'[t] == -b*s[t]*i[t] + r[t]/tr,
i'[t] == +b*s[t]*i[t] - i[t]/ti,
r'[t] == i[t]/ti - r[t]/tr,
s[0] == 0.5, i[0] == 0.5, r[0] == 0},
{s, i, r}, {t, 0, 500}];
Plot[{i[t] /. sol, s[t]} /. sol, {t, 0, 500}, PlotRange -> {0., 1.}]
O sistema de equações diferenciais com atraso pode ser pode ser solucionado via Python utilizando o método de Euler conforme proposto :
import matplotlib.pyplot as plt
import numpy as np
#Função para resolver o sistema de equações diferenciais
def sistema(R0,R1):
#Parâmetro R0=b.ti
#Parâmetro R1=tr/ti
#Parâmetros da dinâmica
b =4
ti=R0/b
tr=R1*R0/b
to=ti+tr
# Listas para guardar a evolução do sistema
s=[]
i=[]
d=0.001 #Passo para o método de Euler
#Primeira parte:
N1=int(ti/d) #Quantidade de passos
i.append(1e-16) #Condição inicial de inectado i0
s.append(1-i[0]) #Condição inicial de suscetíveis s0=1-i0
#Resolve o sistema Usando o método de Euler
for k in range(N1):
s.append(s[k]+d*(-b*s[k]*i[k]))
i.append(i[k]+d*(b*s[k]*i[k]))
#Segunda parte
N2=int(to/d)
for k in range(N1,N2):
s.append(s[k]+d*(-b*s[k]*i[k]))
i.append(i[k]+d*(b*s[k]*i[k]-b*s[k-int(ti/d)]*i[k-int(ti/d)]))
#Terceira parte
N3=int(1800/d)
for k in range(N2,N3):
s.append(s[k]+d*(-b*s[k]*i[k]+b*s[k-int(to/d)]*i[k-int(to/d)]))
i.append(i[k]+d*(+b*s[k]*i[k]-b*s[k-int(ti/d)]*i[k-int(ti/d)]))
O sistema também pode ser resolvido via Mathematica:
b = 0.8; ti = 5; to = 20;
ci1 = NDSolve[{
s1'[t] == -b*s1[t]*i1[t],
i1'[t] == +b*s1[t]*i1[t],
s1[0] == 0.99, i1[0] == 0.01},
{s1, i1}, {t, 0, ti}];
ci2 = NDSolve[{
s2'[t] == -b*s2[t]*i2[t],
i2'[t] == +b*s2[t]*i2[t] - b*s2[t - ti]*i2[t - ti],
s2[t /; t <= ti] == s1[t] /. ci1,
i2[t /; t <= ti] == i1[t] /. ci1},
{s2, i2}, {t, 0, to}];
sol = NDSolve[{
s'[t] == -b*s[t]*i[t] + b*s[t - to]*i[t - to],
i'[t] == +b*s[t]*i[t] - b*s[t - ti]*i[t - ti],
s[t /; t <= to] == s2[t] /. ci2, i[t /; t <= to] == i2[t] /. ci2},
{s, i}, {t, 0, 300}];
Plot[{i[t] /. sol, s[t] /. sol}, {t, 0, 300}, PlotRange -> {0., 1.}]
O código abaixo foi escrito em Python e é responsável por buscas raízes complexas com a parte real positiva na equação transcendental discutida anteriormente.
#Código para resolver a equação transcendental
def raizes():
sol=np.zeros((35,90)) # Matriz para guardar as raízes
err=1e-12 # Erro admitido
sy=0
for R0 in np.arange(1,10,0.1): #Percorrer os valores RO=b.
print(str(100*(sy+1)/90)+"%")
sx=0
for R1 in np.arange(0,3.5,0.1): #Percorrer os valores R1=tr/ti
#Parâmetros da dinâmica
b =4
ti=R0/b
tr=R1*R0/b
to=ti+tr
#Pontos de equilíbrio
io=(b*ti-1)/(b*to)
so=1/(b*ti)
#Matriz das raízes para os parâmetros atuais
r=np.zeros((20, 20))
#Os chutes iniciais serão pontos dentro da malha [-1,1] em 2D
m=0
for a in np.arange(-1,1,0.1):
n=0
for y in np.arange(-1,1,0.1):
i=y*1j
x=a+i # Ponto inicial
N=10000000 # Quantidade máxima de aproximações
#Valor da função para o chute inicial
f=x+b*(so*(np.power(np.e,-x*ti)-1)-io*(np.power(np.e,-x*to)-1))
for k in range(N):
if (k==N-2):
print("!") #Indicando que chegou no último passo sem achar a raízs
if (abs(f)<err):
break # Se chou a raíz, do loop
try:
f =x+b*(so*(np.power(np.e,-x*ti)-1)-io*(np.power(np.e,-x*to)-1))
df=1+b*(to*io*np.power(np.e,-x*to)-ti*so*np.power(np.e,-x*ti))
nx=x-f/df # Próximo chute
x=nx
except:
print(str(R0)+","+str(R1))
break
if(abs(np.real(x))<err): # A raíz é zero
r[m,n]=0
elif (np.real(x)>0): # Raíz positiva
r[m,n]=1
break
else:
r[m,n]=-1 # Raíz negativa
n=n+1
else: # Quando acabar o loop interno
m=m+1
continue # Continua
break # Se o loop interno foi encerrado antes da hora, encerra o externo
res=[]
for i in range(20):
res.append(max(r[i]))
sol[sx,sy]=max(res) # Se houve raíz positiva, obtém.
sx=sx+1
sy=sy+1
#Registra
f = open("raizes.dat", "w")
for i in sol:
for j in i:
f.write(str(j)+" ")
f.write("\n")
f.close()
raizes()
A partir dos dados gerados com o código anterior, é possível visualizá-los em R com o seguinte código:
library('tseries') #Bibliotea pra ler matriz
library('plot.matrix') #Biblioteca pra plotar matriz
m <- read.matrix( "Raizes.dat") #Os dados são lidos no formato de matriz
m<-t(m) # São feitas algumas correções devido à ordem que os dados são gravados
m <-m[90:2, 1:35]
rownames(m) <- (99:11)/10 #Ajusta-se os nomes das linhas e colunas
colnames(m) <- (0:34)/10
#E plota-se
plot(m, col=c('black', 'white', 'green'), breaks=c(-2, -0.25,0.25, 2), xlab='R1', ylab='R0',main='Raizes',border=NA)
Principais materiais utilizados
- Oscillations in SIRS model with distributed delays (S. Gonçalves e outros, The European Physical Journal B)
- Root finding algorithms (Eugeniy E. Mikhailov, Faculdade de William e Mary)
- Stability and stabilization of time-delay systems ( Gerhard Manfred Schoen ,Instituto Federal de Tecnologia de Zurique)

















![{\textstyle \left[-\tau _{0},0\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78093fef9dbf06a6b990659bd088590201247bd7)





























![{\displaystyle {\begin{aligned}{\frac {di\left(t\right)}{dt}}&=\beta s\left(t\right)i\left(t\right)-{\frac {i\left(t\right)}{\tau _{i}}}\\\int _{i\left(t^{*}-\tau _{i}\right)}^{i\left(t^{*}\right)}di&=\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt-{\frac {1}{\tau _{i}}}\int _{t^{*}-\tau _{i}}^{t^{*}}i\left(t\right)dt\\i\left(t^{*}\right)&=\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt+\left[i\left(t^{*}-\tau _{i}\right)-{\frac {1}{\tau _{i}}}\int _{t^{*}-\tau _{i}}^{t^{*}}i\left(t\right)dt\right]{eq:tri}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a453641c87483dc6419ad8f45edce081a2d2c66)






![{\displaystyle i\left(t^{*}\right)=\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt+\left[i\left(t^{*}-\tau _{i}\right)-{\frac {1}{\tau _{i}}}\int _{t^{*}-\tau _{i}}^{t^{*}}i\left(t\right)dt\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c115219a9620bbe48ab9463e822f1d8324cfab7)











![{\displaystyle {\begin{aligned}{\frac {di\left(t\right)}{dt}}=&\beta s\left(t\right)i\left(t\right)-\beta s\left(t-\tau _{i}\right)i\left(t-\tau _{i}\right)\\\int _{i\left(t^{*}-\tau _{i}\right)}^{i\left(t^{*}\right)}di=&\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt-\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t-\tau _{i}\right)i\left(t-\tau _{i}\right)dt\\i\left(t^{*}\right)=&\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt+\left[i\left(t^{*}-\tau _{i}\right)-\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t-\tau _{i}\right)i\left(t-\tau _{i}\right)dt\right]{eq:cat}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd8a500d717706c37e14bf29bc0311f60d2da7ab)





















































![{\displaystyle \det \left[\Delta \left(\lambda \right)\right]=\det \left[\lambda \mathbb {I} -A_{0}-\sum _{i=1}^{k}A_{i}e^{-\lambda T_{i}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af165a4947325d8223f3e6bc9dbe57c2acfbe569)



![{\textstyle \det \left[\lambda \mathbb {I} -A_{0}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/385c1cfaf89279b436eb62e91a64e45625af1385)
![{\textstyle \det \left[\Delta \left(\lambda \right)\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b6401e8e0b97bad294469d0bcb08e63a3cdd426)




![{\displaystyle {\begin{aligned}\det \left[\Delta \left(\lambda \right)\right]=&\det \left[\lambda \mathbb {I} -A_{0}-A_{1}e^{-\lambda \tau _{0}}-A_{2}e^{-\lambda \tau _{i}}\right]\\=&\det \left[\left({\begin{array}{cc}\lambda &0\\0&\lambda \end{array}}\right)-\beta \left({\begin{array}{cc}-i^{*}&-s^{*}\\i^{*}&s^{*}\end{array}}\right)-\beta \left({\begin{array}{cc}i^{*}&s^{*}\\0&0\end{array}}\right)e^{-\lambda \tau _{0}}+\beta \left({\begin{array}{cc}0&0\\i^{*}&s^{*}\end{array}}\right)e^{-\lambda \tau _{i}}\right]\\=&\det \left[\left({\begin{array}{cc}\lambda +\beta i^{*}\left(1-e^{-\lambda \tau _{0}}\right)&\beta s^{*}\left(1-e^{-\lambda \tau _{0}}\right)\\\beta i^{*}\left(e^{-\lambda \tau _{i}}-1\right)&\lambda +\beta \left(e^{-\lambda \tau _{i}}-1\right)s^{*}\end{array}}\right)\right]\\=&\left[\lambda +\beta i^{*}\left(1-e^{-\lambda \tau _{0}}\right)\right]\left[\lambda +\beta \left(e^{-\lambda \tau _{i}}-1\right)s^{*}\right]-i^{*}\beta \left(e^{-\lambda \tau _{i}}-1\right)s^{*}\beta \left(1-e^{-\lambda \tau _{0}}\right)\\=&\lambda ^{2}+\lambda \beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]+\beta ^{2}s^{*}i^{*}\left(e^{-\lambda \tau _{i}}-1\right)\left(1-e^{-\lambda \tau _{0}}\right)-\beta ^{2}s^{*}i^{*}\left(e^{-\lambda \tau _{i}}-1\right)\left(1-e^{-\lambda \tau _{0}}\right)\\=&\lambda ^{2}+\lambda \beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cd8f17768c479c7e3a2cbc539ed13c67fdf6f38)
![{\displaystyle {\begin{aligned}\lambda ^{2}+\lambda \beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/757b2f6a0a8648034d3949191c4098ae1acb152f)

![{\displaystyle {\begin{aligned}\lambda +\beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdf78f7b306aa827762fa0b596e14ff81918e685)








![{\displaystyle {\begin{aligned}f\left(\lambda \right)&=\lambda +\beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]\\f'\left(\lambda \right)&=1+\beta \left[\tau _{0}i^{*}e^{-\lambda \tau _{0}}-s^{*}\tau _{i}e^{-\lambda \tau _{i}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/567b36fa7c40c26cc6255397872da4c824b38e63)
















