Introdução à equações diferenciais com atraso
Anterior: Métodos de Lyapunov | Índice: Ecologia | Próximo: Solução via integrais sucessivas
Antes de começar, duas curiosidades é que a necessidade de trabalhar com equações diferenciais com atrasos tem como um dos marcos iniciais ter sido enfatizado inicialmente por Lotka em modelos epidemiológicos de malária, e a história do desenvolvimento das equações diferenciais com atraso se mistura com das equações intetegro-diferenciais.
Prosseguindo, definindo então como uma variável que descreve o comportamento de um processo no intervalo , para definir uma equação diferencial funcional (functional differential equation - FDE) precisamos definir:
- e são conjuntos de números reais dependentes do tempo definido para todo ;
- é uma função contínua em ;
- é a derivada de .
- Para cada , tem-se onde ;
- Da mesma forma onde .
Ou seja, para cada instante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t} , temos uma função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x_{t}\left(s\right)} que é a função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x} no instante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t} deslocada no tempo por uma quantidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle s} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle s} é retirado do conjunto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle T_{1}\left(t\right)} no instante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t} . Um ponto importante é que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x\left(t\right),T_{1}\left(t\right)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle T_{2}\left(T\right)} são Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n-dimensionais} , então podem representar um sistema de equações. Podemos dizer que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x} satisfaz uma FDE se para quase todo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t\in\left[t_{0},t_{1}\right]} a seguinte igualdade é válida:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{x}\left(t\right)=f\left(t,x_{t},\dot{x}_{t},u\left(t\right)\right)}
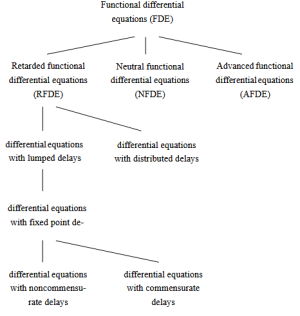
Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u\left(t\right)} é chamado muitas vezes de entrada na teoria de controle e é dado para todo o intervalo de tempo necessário. Essa equação contém três tipos de equações diferenciais:
- Equação diferencial funcional com retardo (retarded functional differential equations - RFDE): Se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle T_{1}\left(t\right)\subset\left(-\infty,0\right]} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle T_{2}\left(t\right)=\oslash} . Isto é, a condição para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle T_{2}} implica que não depende da derivada de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x_{t}} e a primeira condição implica que o deslocamento representa sempre um atraso. Denotando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle T\subset\left[0,\infty\right)} , então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x_{t}\left(s\right)=x\left(t-s\right)} onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle s\geq0} .
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{x}\left(t\right)=f\left(t,x_{t},u\left(t\right)\right)}
Ou seja, em outras palavras, a taxa da variação do estado de uma RFDE é determinado pela entrada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u\left(t\right)} , bem como os estados atuais e passados do sistema.. Em teoria do controle é chamado de sistema com atraso no tempo.
- Equação diferencial funcional neutral (neutral functional differential equations - NFDE): Se a taxa de variação do sistema depende dos seus valores passados, incluindo a derivada, isto é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle T_{1}\left(t\right)\subset\left(-\infty,0\right]} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle T_{2}\left(t\right)\subset\left(-\infty,0\right]} . Um exemplo de sistema escalar linear seria:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{x}\left(t\right)=\dot{x}\left(t-1\right)+x\left(t\right)+u\left(t\right)}
- Equação diferencioal funcional avançada (Advanced functional differential equations - AFDE): parecido com RFDE, mas ao invés do atraso, temos um avanço, isto é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle T_{1}\left(t\right)\subset\left[0,\infty\right)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle T_{2}\left(t\right)=\oslash} . Neste caso a taxa de variação do sistema depende dos seus atuais e futuros valores, além da entrada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u\left(t\right)} .
Uma observação é que RFDE se converte em AFDE para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t<0} e vice-versa. O foco nos próximos tópicos será em RFDE. Se o conjunto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle T_{1}\left(t\right)} é finito para cada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t\in\left[t_{0},t_{1}\right]} , então é chamado de FDE com atrasos discretos. Se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle T_{1}\left(t\right)} é contínuo, então os atrasos são distribuídos. No caso de atrasos discretos, ainda podemos separar em sistemas em que os atrasos são relacionados por inteiros, chamando-os de atrasos comensuráveis. Como por exemplo:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{x}\left(t\right)=A_{0}x\left(t\right)+\sum_{i=1}^{k}A_{i}x\left(t-ih\right)}
E quando não estão relacionados é chamado de incomensuráveis.
Principais materiais utilizados:
- Stability and stabilization of time-delay systems (Gerhard Manfred Schoen, Instituto Federal de Tecnologia de Zurique)
Anterior: Métodos de Lyapunov | Índice: Ecologia | Próximo: Solução via integrais sucessivas


![{\textstyle \left[t_{0}-\tau _{max},t_{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8b2d8075087c058182a64ddfa907d6273c4aa57)


![{\textstyle t\in \left[t_{0},t_{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c0278e66ff704255773b696815d421aef609672)

![{\textstyle \left[t_{0},t_{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35ff44ec79675073f26d48a6815a6e37469e2715)