Clusterização

PÁGINA EM CONSTRUÇÃO

Clusterização do Modelo de Ising

O modelo de Ising é definido como uma malha de tamanho L, quadrada quando em duas dimensões e cúbica quando em três dimensões, onde cada vértice apresenta um componente de spin de magnitude fixa que pode apontar para cima ou para baixo (+1 ou -1, respectivamente). O sistema pode ser descrito pelo seguinte hamiltoniano:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{Ising} = -J \sum_{\langle ij \rangle} s_i s_j}

onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} representa o valor do spin e a soma é feita sobre os pares de vértices próximas que são conectadas com um acoplamento ferromagnético de força Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J > 0} .

Para um modelo de Ising bidimensional (o tipo que consideramos) é possível calcular [1] sua temperatura crítica exata como:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c = \frac{2J}{\log(1 + \sqrt{2})} \simeq 2.269J}

Acima dessa temperatura o sistema está na ‘’’fase paramagnética‘’’, onde a magnetização média é nula, e abaixo dessa temperatura o sistema está na fase ‘’’fase ferromagnética’’’, onde a maioria dos spins se alinham e a magnetização se torna não-nula. Ao estudar o modelo de Ising em geral temos maior interesse no comportamento do sistema perto de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} , onde o sistema forma grupos grandes de spins para cima ou para baixo. Esses grupos contribuem muito para a energia do sistema, causando muita flutuação quando invertem.

O algoritmo de Metropolis é um ótimo algoritmo para realizar simulações do modelo de Ising [1]. Porém, sua dinâmica de flip único é ineficiente especialmente quando próxima da temperatura crítica do sistema. As imprecisões estatísticas de quantidades como magnetização e energia interna do sistema aumentam quando próximo da temperatura crítica. Assim, quando esses grandes grupos de spins alinhados (clusters) invertem, há grandes imprecisões. Essa imprecisão aumenta com o tamanho das flutuações, mas diminui com o número de medidas feitas na simulação, então para se estudar a região perto de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} de modo mais preciso é necessário que a simulação aconteça por mais tempo. Porém, uma outra fraqueza do algoritmo de Metropolis é seu tempo de correlação $\tau$ grande ao redor da temperatura crítica. Isso significa que o número de medidas de uma simulação é pequena, então para diminuir as imprecisões estatísticas causadas pelas poucas medidas é necessário rodar o algoritmo por mais tempo.

Uma das propriedades do modelo de Ising é o fato de flutuações grandes gerarem medidas mais imprecisas. Porém, o tempo de correlação e o modo como ele se comporta próximo a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} é uma propriedade do algoritmo utilizado para estudar o sistema, e então é algo que pode ser otimizado.

Expoentes Críticos

Para estudar mais sobre a eficiência dos algoritmos no modelo de Ising podemos definir a temperatura reduzida como:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = \frac{T - T_c}{T_c}}

Essa grandeza indica o quão distante estamos da temperatura crítica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} , de modo que para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=0} estamos em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} . A partir disso, e sabendo que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} indica a largura médio dos clusters, temos que a expressão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi \sim |t|^{- \nu}} demonstra a divergência da largura de correlação (largura dos clusters). Se tratando do tempo, definimos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau \sim |t|^{-z \nu}} como o tempo de correlação da simulação, medido em passos de Monte Carlo por sítio da rede. O expoente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} , chamado de expoente dinâmico, é um modo de quantificar a diferença de tempo que acontece devido à divergência. Um valor grande de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} simboliza que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} fica grande, por exemplo, fazendo uma simulação mais demorada e menos precisa quando próximo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} .

Combinando as duas equações vistas, podemos escrever que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau \sim \xi^z} . Essa relação indica que o tempo de correlação aumenta com o tamanho típico dos clusters. Considerando um sistema de tamanho finito porém (os tipos de sistema que simulamos), o valor máximo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} vai ser o tamanho Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} do sistema (e.g. um sistema Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 64} xFalhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 64} tem Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L=64} ). Podemos assim concluir que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau \sim L^z} .

Sabendo a temperatura crítica do sistema (para Ising 2D, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c = 2.269J} é possível usar a relação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau \sim L^z} para medir Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} por meio de simulações onde a temperatura do sistema é igual à temperatura crítica para vários tamanhos diferentes de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} , plotando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} versus Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} em escala logarítmica. A inclinação da reta que liga todos esses pontos nos dá o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} .

Por meio desse método, temos que o Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} do algoritmo de Metropolis é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = 2.1655 \pm 0.0012} [5] e o Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} do algoritmo de Wolff (um algoritmo de clusterização) é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = 0.25 \pm 0.001} [6].

O motivo do tempo grande do algoritmo de Metropolis é a divergência do tamanho de correlação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} próximo da temperatura crítica. Ao se aproximar de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} , grandes regiões se formam onde todos os spins estão alinhados, e é demorado para que o algoritmo inverta essas regiões, dado que ele inverte os spins sítio por sítio.

Algoritmos de cluster, como o de Wolff, fazem uso da técnica de clusterização. Com isso, os algoritmos encontram agrupam spins alinhados em clusters que apontam para a mesma direção e invertem os spins desse cluster ao mesmo tempo. Algoritmos de clusterização permitem uma exploração mais efetivo do espaço de fase próximo da temperatura crítica por serem mais eficientes e de precisarem de menos iterações para terem medidas precisas.

Balanço Detalhado

Para respeitarmos o Balanço Detalhado, precisamos que a mudança da rede de um estado $Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} para um estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} ocorra com a mesma probabilidade da mudança de um estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} , denotamos essa mudança por: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(\mu \to \nu) = A(\nu \to \mu)} , com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x \to y)} sendo a razão de aceitação da mudança de um estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} para um estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} .

Supondo que estamos mudando de um estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} para outro estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} , temos que a diferença de energia entre esses dois é resultado da quebra das ligações entre pares de spins orientados na mesma direção que não foram adicionados ao cluster, já que, não há uma garantia que a ida de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu \to \mu } quebre a mesma quantidade de ligações que a volta de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu \to \nu} . A probabilidade de não adicionarmos um spin vizinho ao cluster é dada por: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 - P_{add}} ; uma vez que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{add}} é a probabilidade de incluir esse spin no cluster.

Supondo que existam Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} ligações a serem quebradas na ida de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu \to \mu} , a probabilidade desse evento é dada por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1-P_{add})^m} . Porém, o mesmo pode não valer para a volta de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu \to \nu} , em razão disso, precisamos analisar o caso em que não há o mesmo número de ligações a serem quebradas na volta e então a probabilidade será dada por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1-P_{add})^n} com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} sendo o número de ligações a serem quebradas de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu \to \nu} .

Consideramos agora que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\nu}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\mu}} sejam as energias associadas aos estados Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu } , respectivamente, temos que: a cada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} ligações que são quebradas de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu \to \nu} a energia aumenta com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle +2J} e para cada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} novas ligações geradas de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu \to \nu} a energia diminui com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2J} . Pode-se escrever então que a diferença de energia entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} é dada por: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\nu} - E_{\mu} = 2mJ -2nJ = 2J(m-n)}

Seguindo a definição do Balanço Detalhado e impondo que o Processo Markoviano dessas mudanças de estados descritas acima respeite a Distribuição de Boltzmann, precisamos que: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{(1-P_{add})^m A(\mu \to \nu)}{(1-P_{add})^n A(\nu \to \mu) } = e^{-\beta(E_{\nu} - E_{\mu})} = (1-P_{add})^{m-n}\frac{A(\mu \to \nu)}{A(\nu \to \mu)}} , tal que, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{A(\mu \to \nu)}{A(\nu \to \mu)} = \big[e^{2\beta J}(1-P_{add})\big]^{n-m}\;\;\;\; \Longrightarrow P_{add} = 1-e^{-2\beta J} \Longrightarrow \frac{(1-P_{add})^m A(\mu \to \nu)}{(1-P_{add})^n A(\nu \to \mu) }=1 }

Algoritmo de Wolf

Dinâmica do Algoritmo

O algoritmo de Wolff baseia-se principalmente em 4 passos. são estes:

• 1 - Escolhe-se um sítio aleatório da rede;
• 2 - Entre seus 4 vizinhos, se o spin do vizinho for igual ao do sítio inicial, adicionamos o vizinho ao cluster com probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{add} = 1-e^{2\beta J}}
• 3 - Para cada vizinho que foi adicionado ao cluster no passo anterior, repetimos o processo do passo 2 adicionando os vizinhos desse vizinho que possuem spin na mesma direção com a mesma probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{add}} . Faz-se isso para todos os sítios que são adicionados ao cluster.
• 4 - Quando todos os vizinhos de todos os sítios adicionados ao cluster tiveram ao menos uma “chance” de serem adicionados ao cluster, flipamos o cluster.

Dinâmica do algoritmo.
Demonstração da dinâmica de clusterização do algoritmo na temperatura crítica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \; T_c = 2.269J } .

Simulações

Animações

Animações do algoritmo de Wolff em função da Temperatura Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} .
Simulação para temperatura abaixo da temperatura crítica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} .	Simulação na temperatura crítica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} .	Simulação para tempetura acima da temperatura crítica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} .

Propriedades do Algoritmo de Wolff

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{add}\;= \;1 - e^{-2\beta J} }

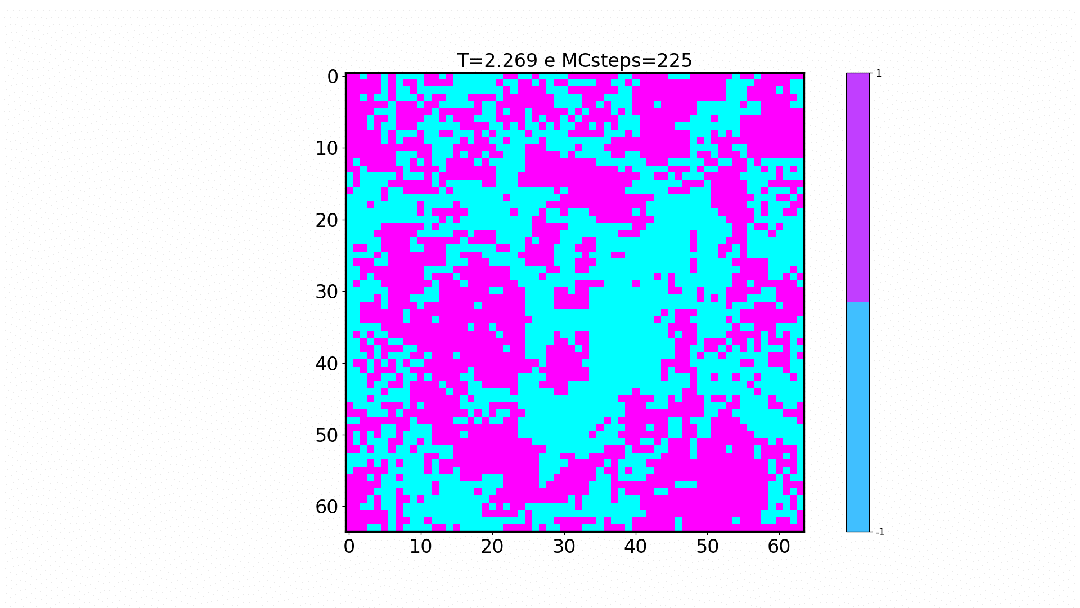
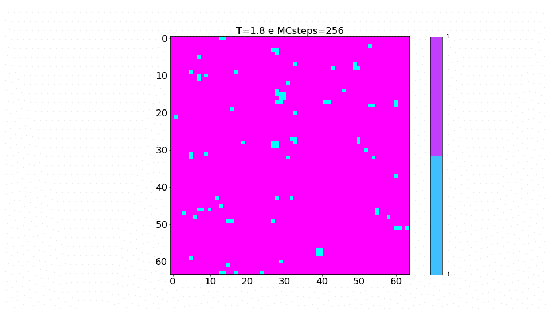
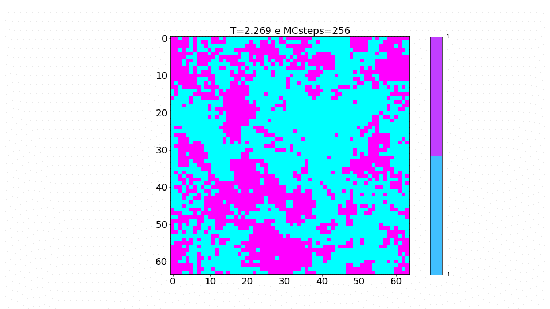
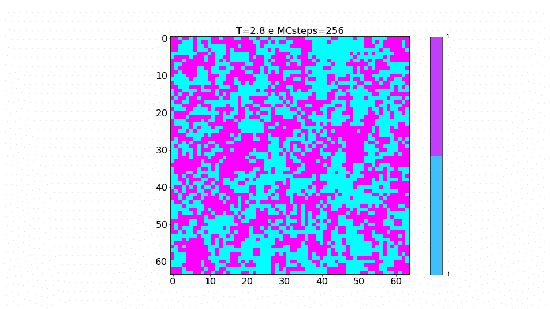
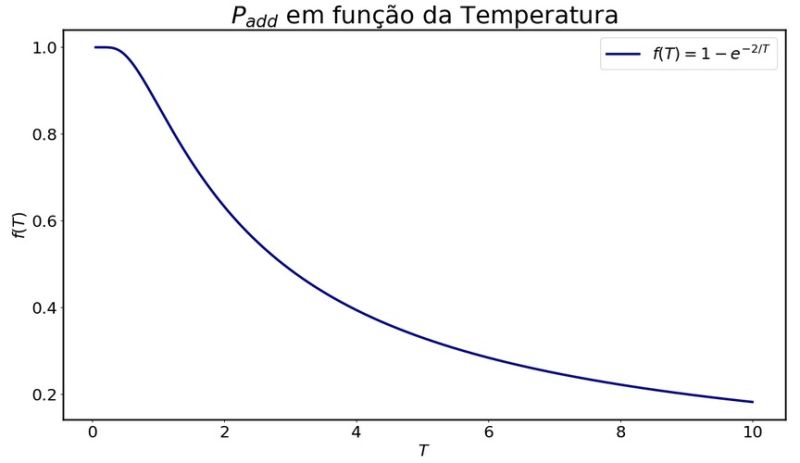
Nas animações acima, pode-se perceber que a temperatura tem papel importante na dinâmica apresentada em decorrência da forma com a qual está relacionada a probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{add}} , como podemos ver o gráfico a seguir:

Probabilidade em função da temperatura.

Gráfico da probabilidade de aceitação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{add}} em função de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T}

Neste gráfico temos a probabilidade de um spin que possui a mesma orientação que o sítio inicial escolhido ser aceito e adicionado ao cluster em função da temperatura da rede. É de se esperar que conforme a temperatura aumente a probabilidade do spin ser adicionado ao cluster diminua e para temperaturas mais baixas espera-se o contrário. Com base nisso, podemos formular a ideia do tamanho médio dos cluster (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_s} ) que é invertido durante os passos de Monte Carlo em função da temperatura e associar este tamanho com a fração representada por este na rede.

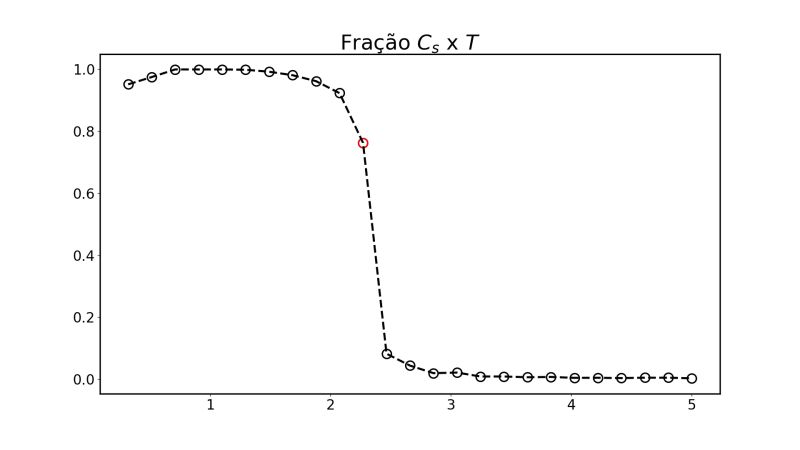
Fração do Tamanho dos Clusters (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_s} )

No gráfico abaixo podemos perceber a mesma natureza que foi observados nas animações desenvolvidas, já que a fração do tamanho dos cluster diminui conforme a temperatura aumenta, ou seja, com a temperatura alta os clusters são menores e por isso representam uma fração menor e para temperatura acima de 3J essa fração é quase zero. Já para temperaturas mais baixas, essa fração aproxima-se de 1 o que significa que grande parte da rede, ou praticamente toda a rede, está sendo invertida em cada passo; exatamente o que observamos na animação para T=1.8J.

Gráfico de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_s} .

Gráfico de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_s} em função de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T}

Série Temporal para a medida de magnetização

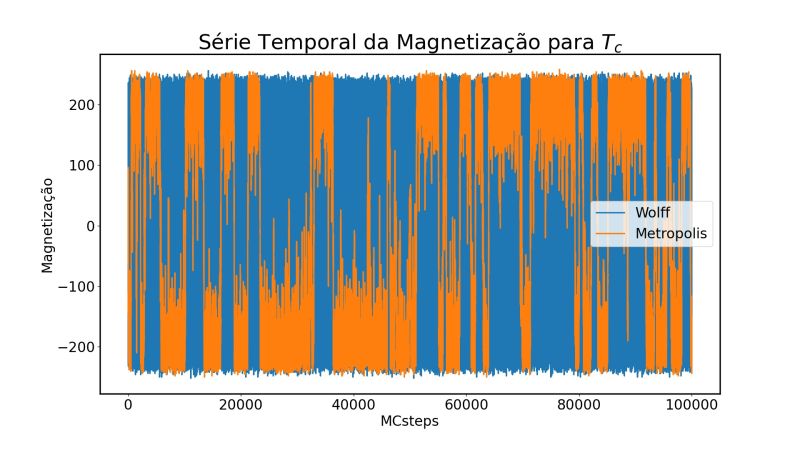
Série Temporal da magnetização.
Gráfico da série temporal da medida de magnetização comparando os algoritmos

Podemos observar na figura acima medidas da magnetização usando o algoritmo de Wolff e o algoritmo de Metropolis para um sistema Ising 2D de mesmo tamanho (16x16) na temperatura crítica (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c=2.269J} ). Nota-se que o algoritmo de Wolff explora o espaço de fase ao redor dessa temperatura em muito menos passos que o algoritmo de Metropolis, sendo mais eficiente para se obter medidas precisas ao redor dessa região.

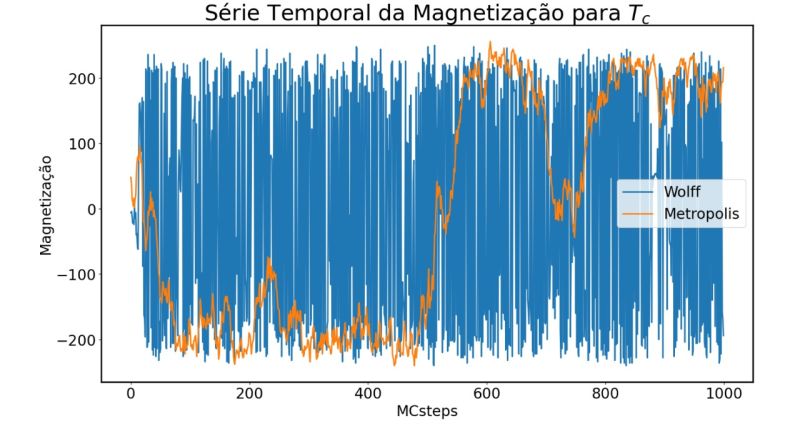
Na figura abaixo podemos observar esse mesmo sistema para um número menor de passos. É possível notar que para que o algoritmo de Metropolis inverta os clusters de spins alinhados a fim de chegar nos mesmos limites dos valores de magnetização há uma demora muito maior de tempo, que se deve à sua dinâmica de single spin flip. Nesse caso, enquanto Wolff já explora o espaço de fase ao redor de T_c em menos de 100 passos, Metropolis precisa de pelo menos 600 passos.

Esse comportamento é o que esperamos dado a desaceleração crítica (critical slowing down), onde a medida que o sistema aumenta de tamanho se torna mais difícil de gerar configurações estatisticamente independentes [3]. Os clusters do algoritmo de Wolff mitigam esse efeito, sendo um sistema muito eficiente para eliminar correlações não locais.

Série Temporal da magnetização até 1000 passos.
Gráfico da série temporal da medida de magnetização comparando os algoritmos nos primeiros 1000 passos

Códigos Fonte

Função da Dinâmica de Clusterização

def cluster_din(sitio):
    stack = []
    oldspin = s[sitio]
    newspin = (-1)*s[sitio]
    s[sitio] = newspin
    sp=1
    stack.append(sitio)
    
    while (sp):
        sp = sp-1
        atual = stack[sp]
        stack.pop()        
    
        for j in range(4):
            nn=viz[atual][j]
            if s[nn] == oldspin: #IF da orientação do vizinho
             rfloat1 = rng.random()
             if (rfloat1<prob) : #IF da inclusão no cluster
                 stack.append(nn)
                 sp = sp+1
                 s[nn] = newspin
    return

Função do Cálculo da Magnetização

def cluster_din_mag(sitio, mag):
    stack = []
    oldspin = s[sitio]
    newspin = (-1)*s[sitio]
    s[sitio] = newspin
    mag = mag +2*s[sitio]
    sp=1
    stack.append(sitio)
    
    while (sp):
        sp = sp-1
        atual = stack[sp]
        stack.pop()        
    
        for j in range(4):
            nn=viz[atual][j]
            if s[nn] == oldspin:   
             rfloat1 = rng.random()
             if (rfloat1<prob) : #IF da inclusão no buffer
                 stack.append(nn)
                 sp = sp+1
                 s[nn] = newspin
                 mag = mag +2*s[nn]
    return mag

Conclusão

Conclui-se então que os resultados obtidos com o códigos produzidos estão, de certa forma, de acordo com o esperado e fez-se possível elucidar as diferenças entre as duas dinâmicas dos algoritmos (Metropolis e Wolff) mostrando os pontos positivos do algoritmo de Wolff e as razões pelas quais se sai melhor na geração de dados estatisticamente independentes do modelo de Ising 2D. Todos os códigos, imagens e gifs gerados para esta apresentação estão disponíveis em: https://github.com/mgteus/MonteCarlo.

Referências

[1] M. E. J. Newman, G. T. Barkema, "Monte Carlo Methods in Statistical Physics". Oxford University Press Inc., New York, 1999.

[2] Materias da disciplina disponíveis em: <https://moodle.ufrgs.br/course/view.php?id=80767>

[3] E. Luijten, “Introduction to Cluster Monte Carlo Algorithms” <http://csml.northwestern.edu/resources/Reprints/lnp_color.pdf>

[4] <https://fiscomp.if.ufrgs.br/index.php/Ising_2D>

[5] Nightingale and Blöte (1996).

[6] Coddington e Baillie (1992).